立式高湿盐泥粉碎机的结构参数研究*

朱桂华,唐浩亭,易山圳,何伟泽,陈 勇

(1.中南大学 机电工程学院,湖南 长沙 410083;2.湖南中大山水环保科技有限公司,湖南 长沙 410000)

0 引 言

盐泥是制盐工业中卤水净化的产物,当前我国盐行业对盐泥的处理方式一般为回井和堆放。这样的处置方式不仅加剧了环境的污染,也浪费了盐泥的可利用价值,因此需要一种新型工艺对盐泥进行无害化、资源化处理,笔者对该工艺中的一环[1]进行研究。

含水率15%以上的块状物料被称为高湿物料,高湿物料因水分含量过高在进行粉碎时常常会粘结在粉碎设备上,导致电机负载加大,效率降低,甚至烧坏电机,严重影响生产。在普通物料粉碎方面,学者们进行了大量的研究。曹丽英等[2-3]研究了粉碎机筛片的结构参数和分离装置的气流速度对筛分效率之间的影响规律;王德福等[4]得出了玉米秸秆的主要粉碎形式及合适的粉碎机运行参数;马彦军等[5]建立了破碎函数的数学模型,为圆锥破碎机破碎过程中破碎生产率的动态优化提供了理论模型。

这些研究结果并不适用高湿物料的粉碎,主要是因为:(1)国内外研究的多数为含水率较低的物料,这类物料粘性小,几乎没有粘壁情况[6];(2)国内外的成果主要集中在农业、饲料和岩石等行业[7],没有盐泥粉碎方面的研究;(3)粉碎机的转子结构还停留在普通的刀片和锤片结构,没有用链条类的柔性结构进行试验分析;(4)当前物料粉碎的研究成果中,大多数通过定性分析的方法来指导粉碎机的设计,统一适用的定量研究分析成果不多。

本文将以自制立式盐泥粉碎机为研究对象,设计双刀片、双链条及刀片链条组合式3种转子结构,采用试验的方法研究3种转子结构在不同转速下对粒径分布以及粘壁厚度的影响。

1 盐泥物理特性及粉碎机结构

1.1 盐泥物理特性

盐泥资源化处理项目的工艺为:

(1)在盐泥储泥罐添加药剂和絮凝剂,令盐泥加速沉降;

(2)通过固液分离设备对盐泥进行深度固液分离,得到盐泥泥饼;

(3)利用粉碎机对盐泥泥饼进行粉碎制粒;

(4)对粉碎过后的盐泥颗粒进行烘干,使其成为燃煤脱硫剂。

盐泥物理特性参数如表1所示。

表1 盐泥物理特性及成分

1.2 粉碎机结构的提出

盐泥粉碎机主要由电机、皮带轮、转子部件、粉碎室以及转子支撑架等组成。

笔者提出一种双刀片、双链条及刀片链条组合式3种转子结构。

其中,刀片链条组合结构如图1所示。

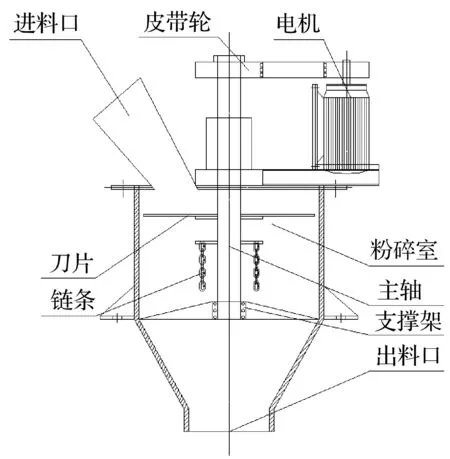
图1 刀片链条组合式粉碎机结构

2 盐泥粉碎及粘附机理分析

通过观察发现,盐泥粉碎的主要形式是打击粉碎和撞击粉碎,同时颗粒与颗粒之间也有接触力作用。打击粉碎是指高速旋转的刀片和链条打击盐泥泥饼发生的粉碎现象,撞击粉碎是盐泥经打击初碎后与壁面发生的粉碎现象[8-9]。由于盐泥泥饼含水率较高且具有粘性,在撞击粉碎过程中有小部分盐泥颗粒会粘附在粉碎机壁面上。

颗粒和刀片,颗粒和颗粒间的整体受力分析如图2所示。

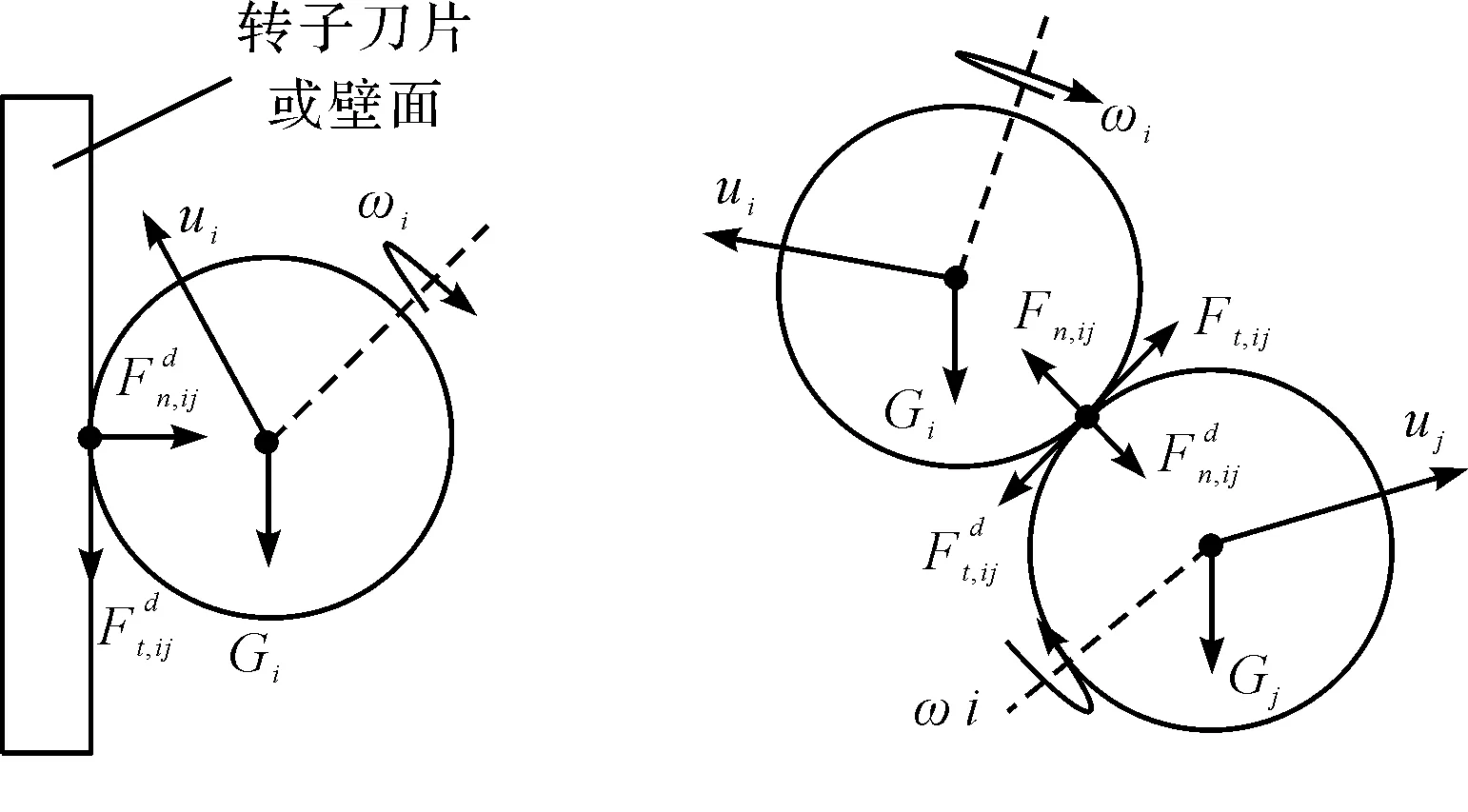
图2 整体受力分析图

(1)

(2)

(3)

Ft,ij=-δtSt

(4)

(5)

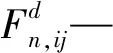
由图2可知:颗粒在运动过程中受重力Gs,i和颗粒碰撞接触力Fc,ij。根据牛顿第二定律可得,颗粒在t时刻的运动状态方程[10-11]为:

(6)

(7)

式中:m—颗粒i的质量;us,i—速度;Ii—颗粒i的转动惯量;ωi—角速度;Tt—为切向力矩;Tr—滚动摩擦力矩;i—颗粒i接触对象编号;j—颗粒j接触对象编号。

2.1 打击粉碎

当盐泥泥饼由皮带机输送至进料口后,高速旋转的刀片及链条和盐泥泥饼发生碰撞,一部分盐泥泥饼经过打击后和壁面进行撞击,另外一部分盐泥泥饼被击飞到刀片上部,导致掉落下来发生二次碰撞。

不考虑粉碎室内的气流和转子的自重,根据冲量-动量定理可知:

FΔt=m(v1-v2)

(8)

(9)

式中:F—刀片对盐泥泥饼的打击力;Δt—打击时间;m—盐泥泥饼的质量;v1—刀片打击速度;v2—盐泥泥饼接触刀片时的速度。

打击力越大,泥饼粉碎效果越好,但粘壁厚度会相对增加。由式(9)可知,打击力的大小和盐泥泥饼的质量、刀片的速度、盐泥泥饼的速度及打击时间有关。泥饼相对于刀片的速度越大,打击力越大;打击作用时间越短,盐泥泥饼受到的打击力越大;打击时间和盐泥的硬度有关,硬度高则打击时间短。

另外,第一次打击前盐泥还未破碎,质量相对较大,打击力大;破碎后被击飞到上部等待第二次打击的泥饼质量减小,打击力相对减小。

2.2 撞击粉碎

盐泥泥饼受刀片打击之后,以较高的速度撞击粉碎机壁面,当撞击力大于泥饼内聚力时泥饼会产生进一步破碎。

根据冲量—动量定理,泥饼与壁面的撞击力为：

(10)

式中:F1—盐泥泥饼与壁面的撞击力;vn—盐泥泥饼接触壁面时的速度:m—盐泥泥饼撞击前的质量;Δt1—撞击时间;λ—盐泥泥饼的弹性恢复系数;α—盐泥泥饼对壁面的入射角。

由式(10)可知,盐泥泥饼与壁面发生撞击的撞击力和撞击前的速度vn以及盐泥泥饼的弹性恢复系数有关。撞击速度vn随着第一次打击力的增大而增大,泥饼弹性恢复系数与其含水率和弹性模量有关。

2.3 粘结机理分析

由于盐泥含水率约为30%,且具有粘性,在撞击粉碎的同时会有一小部分的盐泥颗粒粘结在粉碎室的壁面上。对于完全粘结在壁面上的盐泥小颗粒,粘结过程遵循牛顿第二定律,由于颗粒很小,可将颗粒看作球体。

忽略重力及气流阻力等影响,其粘结方程为:

(11)

式中:s—碰撞点指向球心的压缩位移;Fad—颗粒和壁面粘性力;Fc—颗粒和壁面件的弹性力。

其中,弹性力Fc与物料的弹性模量E和泊松比μ有关,最大可压缩位移Smax受物料碰撞之前的速度v影响,速度越大,最大可压缩位移越大。因此,减少碰撞前的速度能够很好地减小物料和壁面的粘结力。

3 试验方法

笔者通过调节变频器的频率对粉碎机主轴进行调速,每次试验数据记录完毕之后更换对应的转子结构。本文主要考察转子结构和转子转速两个因素对物料的粉碎粒度和粘壁厚度影响。

根据上节理论分析和预实验的效果,笔者最终确定了3种结构方式和6个转子转速的参数水平。

试验的因素水平表如表2所示。

表2 试验因素水平表

在项目现场,笔者采用自行研制的立式粉碎机进行试验，具体的试验步骤如下:

(1)通过预实验,确定可行的转子转速并制作数据记录表;

(2)将制作好的转子结构安装至粉碎机,调节变频器获得试验所需的转子转速;

(3)设置合适的物料进给量和进料速度,依次启动粉碎机和进料皮带机对物料进行粉碎作业。粉碎完成,关闭电源;

(4)每隔0.5 h,用游标卡尺测量粉碎室壁面物料粘结厚度,并记录;

(5)将粉碎过后的物料进行筛分并对每个筛分区间的颗粒进行称量。记录每次试验结果,对试验数据进行处理。

4 试验结果与分析

4.1 粒径分布

由于实际生产需要,笔者以20 mm以下粒径质量占比为评价指标表征粉碎机的性能,通过大量试验得到数据,同时剔除异常数据。

所得到的颗粒粒径质量分布表,如表3所示。

笔者对粉碎后的粒径进行分析,在不同转子转速下,双刀片、双链条及刀片链条组合3种转子结构的粒径变化曲线如图3所示。

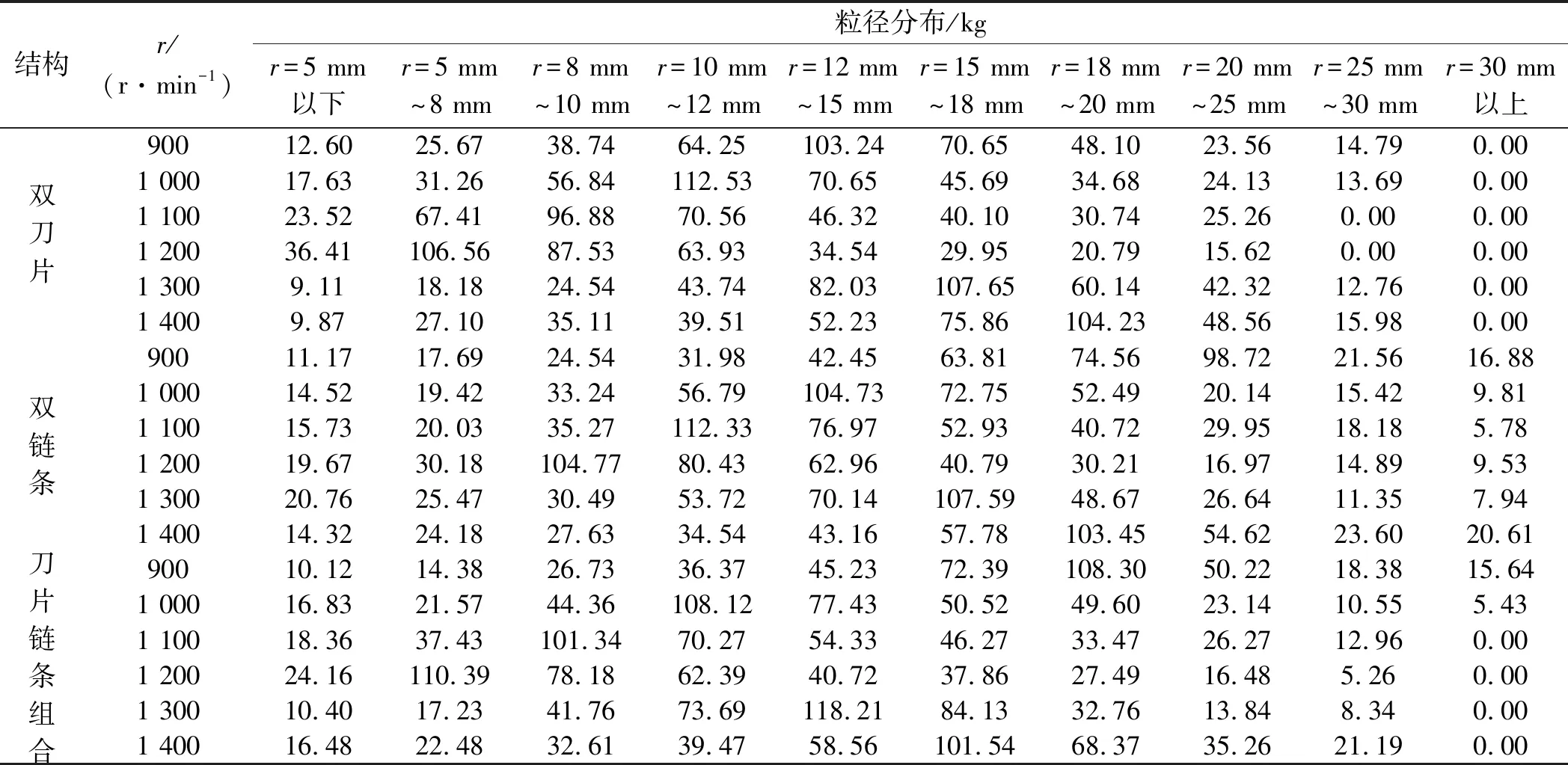
表3 颗粒粒径质量分布

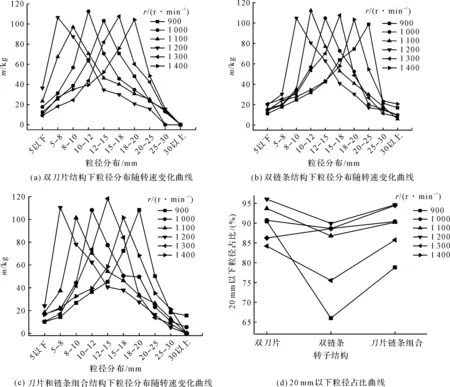
图3 不同转子结构和转速下的粒径分布曲线

由图3可知:

(1)转速对粒径分布的影响要大于转子结构对其的影响,随着转子转速的增加,粒度逐渐减小,粉碎效果越好;

(2)以小于20 mm的粒径占总质量的比值为衡量指标,双刀片结构和刀片链条组合结构的粉碎效果优于双链条结构,随着转速的增大,小颗粒比重逐渐减小。1 200 r时双刀片、双链条和刀片链条组合20 mm以下粒径占比分比为96.0%、89.9%和94.6%,小颗粒粒径比重最大,粉碎效果最佳;当转速超过1 200 r/min时,粉碎颗粒向大粒径方向偏移,这是由于转速过大,赋予第二次粉碎的颗粒能量就大,导致粉碎后的一部分小颗粒之间互相粘结,但再次粘结后的颗粒间粘结键强度远小于初始物料的粘结键强度。

4.2 粘壁厚度

由于盐泥泥饼是含水率为25%～30%的粘性物质,在粉碎过程中会出现粘壁现象。

粉碎机粘壁厚度的试验数据如表4所示。

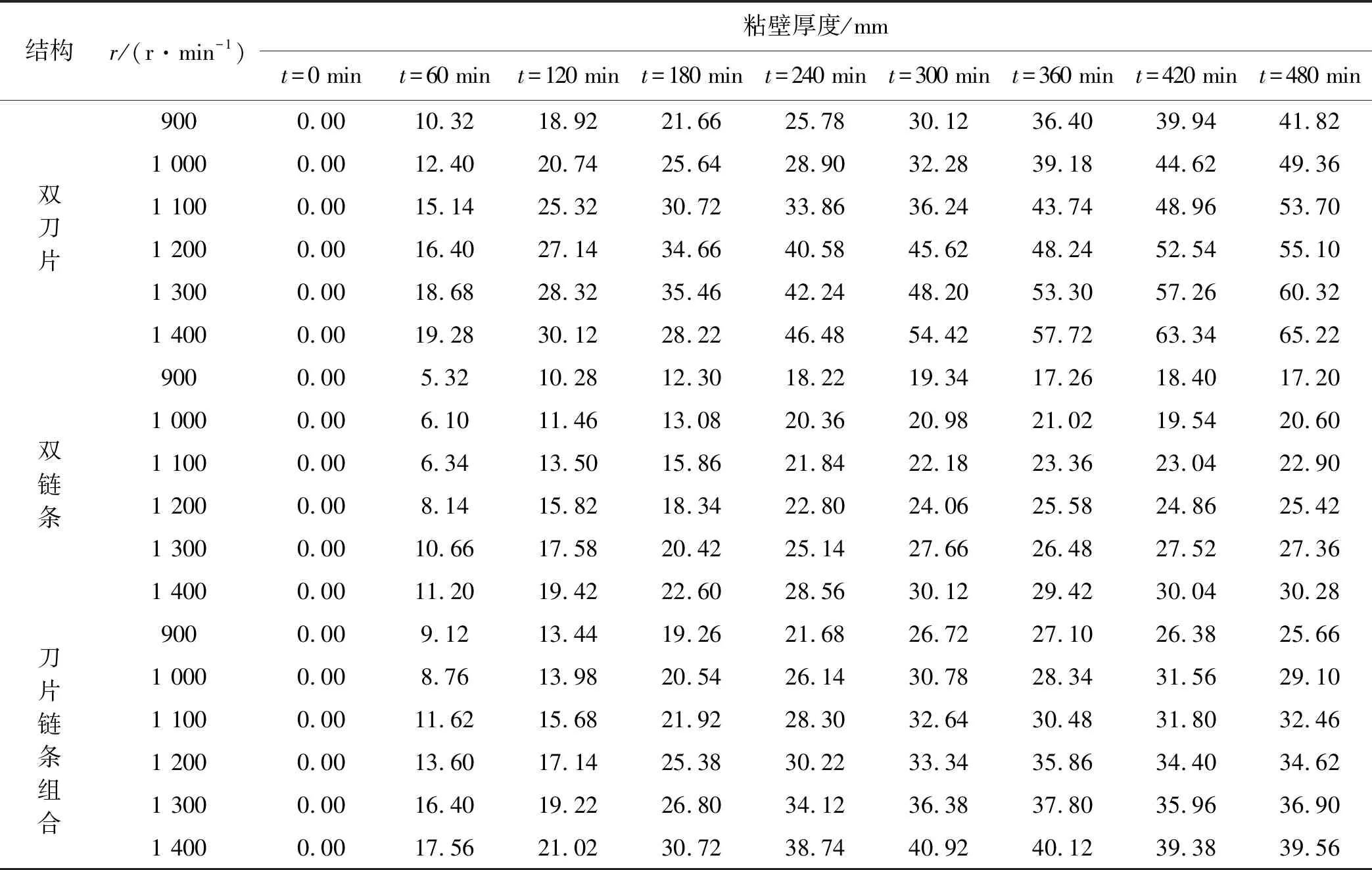
表4 不同转子结构和转速下的粘壁厚度变化

由表4可知:粘壁现象会使粉碎机的粉碎效率降低,甚至造成粉碎机停车。通过分析粘壁现象可以选择更好的结构和运行参数,有效地提高粉碎机的粉碎效率。

根据表4所得的试验数据,笔者绘制了粘壁厚度随转子结构和转子转速的曲线,如图4所示。

由图4可知:

(1)粘壁厚度起初增速很大,随后逐渐减小。随着转速的增加,粘壁厚度也随之增加,与上节粘结机理分析相吻合。当转子结构为双刀片结构时,粘壁厚度一直增加,而双链条和双刀片结构则逐渐趋于稳定。相同转子结构,同一时刻,不同转速下,粘壁厚度最大差值分别为23.40 mm、13.08 mm、17.06 mm;相同转速下,同一时刻,不同结构下,粘壁厚度最大差值分别为24.62 mm、28.76 mm、30.08 mm、29.68 mm、32.96 mm、34.94 mm。从数据可以看出,结构不同,粘壁厚度差值越大,表明粉碎机转子结构对粘壁厚度的影响大于转子转速;

(2)双刀片结构的粘壁厚度持续增长,而双链条结构和刀片链条结构的粘壁厚度逐渐趋于稳定,稳定的时间分别为240 min和300 min,这是因为粘壁厚度与颗粒撞击壁前的速度有关,刀片为刚性打击装置,打击后的速度大,链条为柔性打击装置,在打击过程中末端的链节会绕链环进行转动,可以有效地降低撞击速度,抑制粘壁厚度无限制增长,因此,将粘壁厚度稳定的时间称之为柔性粘壁拐点。

该拐点对盐泥泥饼粉碎机的设计有重要的指导意义。

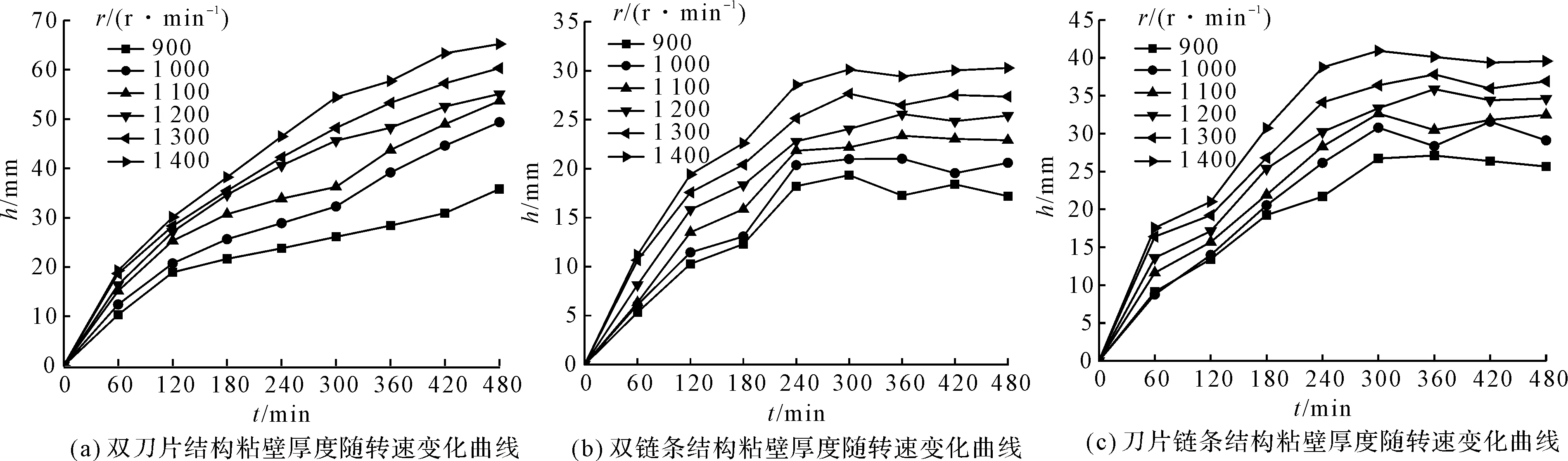
图4 不同转子结构和转速下的粘壁厚度变化曲线

4.3 粒径分布选择函数

粒径分布函数能够有效地表征粉碎颗粒的分散程度,也可以预测粒径的分布范围[12]。笔者利用MATLAB对得到的试验结果,按正态分布、对数正态分布和R-R分布进行拟合。根据拟合所得到的数据发现,盐泥破碎后的粒径遵循R-R分布函数。

由于篇幅有限,现只给出R-R拟合函数、破碎程度指数λ、破碎程度指标数n以及回归值R2。

R-R的函数表达式为:

(12)

式中:F(d)—累积量的百分数;d—粒径尺寸;d50—粒径累计质量分布F为50%对应的粒径尺寸;n—破碎性指标[13]。

为了便于数据分析和拟合,将式(12)改写为:

F*(D)=ln{-ln[1-F(d)]}=nlnd+λ

(13)

λ=-nln(d50)

(14)

式中:λ—破碎程度指数;n—破碎程度指标[14]。

根据式(14)可得到3种结构下颗粒累计质量分数随转速的拟合函数及回归值R2,如表5所示。

表5 粒径分布选择函数的拟合公式

由表5可知:

(1)R2大于0.9的占比为83.3%,拟合效果较好,拟合结果可以用来预测颗粒的粒径分布;

(2)粉碎程度通常用来表征粉碎后的小颗粒粒径占总破碎量的比例,λ越大占比越大。3种结构下,转速为1 200 r/min时,λ值分别为-0.284 36、-0.609 99和-0.351 90,小颗粒比重最大,粉碎效果最好;相同转速下,双刀片和刀片链条组合结构的粉碎效果相差无几,均优于双链条结构,与试验结果吻合。同种结构,不同转速λ差值最大为0.420 88,相同转速,不同结构下λ差值最大为0.218 38,说明转速对粉碎后的小颗粒分布的影响大于转子结构;

(3)粉碎特性指标n用来表征粉碎后颗粒的均匀程度,n值越大,颗粒分布越均匀,从表5中数据可以看出3种结构不同转速下的n值相差较小,说明粒度均匀性相当。3种结构下,转速为900 r/min、1 300 r/min及1 400 r/min时,粒度均匀性稍高于其他转速,但平均粒度集中在20 mm以上,和4.1所得出的随着转速的增加,小颗粒会再次粘结的结论相吻合。

5 结束语

本文以自制的式盐泥粉碎机为研究对象,设计了双刀片、双链条及刀片链条组合式3种转子结构;在不同转速下,采用试验法研究了3种转子结构对粒径分布以及粘壁厚度的影响,得到以下结论:

(1)转子转速对粒径分布的影响大于转子结构,而转子结构对粘壁厚度的影响要大于转子转速。当转子结构为刀片链条组合式结构时,20 mm以下粒径占比均在75%以上,和双刀片结构相差无几,优于双链条结构;双链条和链条刀片组合式结构的粘壁厚度随着时间的增长逐渐趋于稳定,而双刀片则持续增加。综合粒径分布、20 mm以下粒径占比及粘壁厚度的影响,最终选定链条刀片组合式结构为盐泥粉碎机的转子结构;

(2)随着转速的增加,颗粒粒径分布随着转速的增大逐渐向小粒径方向偏移,20 mm以下粒径占比增加,当转速为1 200 r/min时,3种结构20 mm以下粒径占比分别为96%、90%和95%,比重最大,粉碎效果最好。转速超过1 200 r/min时,由于盐泥具有粘性,在粉碎过程中小颗粒会重新发生粘结,20 mm以下粒径占比增大，笔者选定1 200 r/min为盐泥粉碎机工作时的运行参数;

(3)柔性粘壁拐点:由于双链条和刀片链条组合式结构中链条为柔性装置,在打击过程中末端的链条会在一定的速度条件下绕链环进行转动,可以有效地降低撞击速度,抑制粘壁厚度无限制增长。因此在这两种结构下,粘壁厚度随着转速的增大而增大,最终趋于平稳,平稳时间分别为360 min、240 min和300 min;

(4)通过MATLAB软件对数据进行分析,选择合适的粒径分布函数,并对函数进行拟合后发现,盐泥破碎后的粒径遵循R-R分布函数，回归值R2大于0.9的占比为83.3%,拟合效果较好；根据粉碎程度及粉碎特性指标n对粉碎后的粒径分布和均匀程度进行分析后发现和试验结果吻合,因此,该结果可以用来预测颗粒的粒径分布。