固井二界面泥饼固化强度室内评价方法建立

步玉环， 周林维， 杜嘉培， 郭炳亮， 赵乐天

(中国石油大学(华东) 非常规油气开发教育部重点实验室，山东 青岛 266580)

0 引 言

在固井过程中，由于井壁上泥饼的存在，导致水泥石不能直接与井壁胶结，易形成水泥环与井壁(即二界面)之间的微间隙，从而造成固井二界面胶结质量差[1-5]。目前，为解决该问题，除了研究高效冲洗隔离液提高对泥饼的清洗能力外，泥饼固化技术逐渐成为解决固井二界面胶结质量问题的有效方法[6-7]。

从钻井液转化为固井液(MTC)固井技术到泥饼防地成凝饼(MTA)固井技术，以及多功能钻井液的研究，其本质都是在固井水泥石和井壁之间形成具有一定强度的隔层[8-11]。泥饼固化后具有薄而韧的特性，可以有效避免固井二界面的封隔失效问题，但是，如何在实验室中评价固化泥饼的质量成为了现阶段存在的关键问题。常规的泥饼强度评价方法大部分只能定性评价泥饼质量，或者只能间接定量评价泥饼强度[12]。本文建立的固化泥饼强度评价方法操作简单、灵活可靠，可直接根据实验参数计算泥饼强度，为泥饼固化技术的研究提供可靠的评价方法。

1 泥饼固化强度实验方法

1.1 固化泥饼制备方法

泥饼的制备方法采用滤失成饼法，即将钻井液基浆、含有泥饼固化材料的钻井液体系放入滤失筒中，在0.7 MPa压力下滤失一定时间后得到具有一定厚度的泥饼。图1所示为钻井液基浆(左)和含有泥饼固化材料的钻井液体系(右)所形成的泥饼。

图1 滤失法形成的泥饼

泥饼的强度激活方法主要采用渗滤法，即采用失水筒加压使激活剂渗透进入泥饼，试验压力1 MPa，实验温度75 ℃。激活剂采用硅酸钠和氢氧化钠的水溶液，其中硅酸钠和氢氧化钠的质量比为40∶1。经过激活剂作用后，通过观察和初步定性检测，泥饼具有了一定的强度和硬度，因此证明该固化方法的可行性，即通过潜活性材料复配改性钻井液，采用渗滤法制备改性泥饼，之后通过激活剂对泥饼进行激活，形成具有一定强度的泥饼，从而实现二界面的整体固化[13]。

1.2 泥饼固化强度测试装置

受水泥浆初终凝测定方法的启发，笔者进行固化泥饼突破极限载荷的测量装置的改进，其结构如图2所示。其中，支架上方的金属杆可自由移动，金属杆末端嵌入高强度钢针，压力传感器放置于底座中心。在测试过程中，将制备的泥饼放置于压力传感器上，操作金属杆向下缓慢释放使钢针作用于泥饼，记录钢针破坏泥饼时压力传感器的示数，此时测得泥饼承受针入突破的极限力(单位为N)。

图2 泥饼强度评价装置结构图

1.3 泥饼固化强度测试步骤

泥饼固化强度的测试思路为：形成泥饼—激活泥饼—固化强度评价。

具体步骤为：

(1)利用泥饼制备方法制备待评价的固化泥饼。

(2)校核泥饼固化强度评价装置的金属杆自由移动情况，确保金属杆自由移动且不受阻力影响。

(3)校核泥饼固化强度评价装置的压力传感器的灵敏度，以便保证对固化泥饼极限突破力的准确测量。

(4)调整底盘高度，保证控制旋钮完全释放后钢针与测力传感器底盘刚刚不接触，即此时压力传感器不受力的作用。

(5)将制备好的泥饼放置于压力传感器盘上，释放控制旋钮使金属杆自由下落，此时钢针突破固化泥饼，泥饼受力后传至压力传感器，记录该力值。

(6)将泥饼移动一位置，避免钢针落入已经测定的插孔内，重复步骤(5)进行突破力的重复测量(至少3次)。

(7)将多次测定的极限突破力进行加权平均，得到固化泥饼的极限突破力。

2 二界面泥饼固化强度评价方法的建立

在建立的固化泥饼强度评价装置的测试中，只能测定泥饼的极限突破力，但强度的表征一般采用单位面积的受力表示，需要进行力的转化。虽然在钢针突破泥饼时只是顶面1 mm的接触，但在钢针运行中泥饼所受的作用较为复杂，一方面泥饼受到钢针在1 mm圆形范围内的压强作用，但泥饼底部受到完全的支撑；另一方面由于泊松效应，泥饼受钢针作用变形区域会受到周围泥饼的影响。

由于泥饼的受力复杂，通过常规计算手段使得转化过程十分困难，为此，采用了数值模拟的方法，利用ABQUS软件建立泥饼模型，并设置模型各项参数与实际泥饼模型相同，对其进行受力分析，并得出泥饼极限突破力与泥饼强度之间的关系。

2.1 泥饼正向受力转化抗压强度的依据

在材料破坏分析中，采用了Mises屈服准则作为泥饼破坏的强度准则。Mises屈服准则统一了单向拉压状态的第1强度理论、复杂应力状态的第3强度理论和第4强度理论，尤其在复杂应力状态有限元数值分析中，Mises屈服准则获得了更为广泛的应用[14]。本研究采用Mises应力准则的依据为：①采用自制泥饼测量装置测试泥饼强度，泥饼受力条件复杂：包括钢针对泥饼1 mm圆形区域的压强、圆形区域周围的挤压、泥饼底部的支持力以及泥饼发生变形后受力区域周围的挤压。Mises屈服准则适用于复杂应力状态的数值分析，并且所需主要参数通过本实验室的测量设备测得；②泥饼本身不受静水压力的影响，有效减小了Mises屈服准则的使用误差；③泥饼不同于普通的混凝土材料，具有一定的弹韧性(见图3)。通过实验发现，泥饼破坏处四周有细微的裂纹，可判定其破坏形式具有韧性断裂的特征，此种破坏形式由最大Mises应力控制，因此使用Mises屈服准则更准确可靠[15]。

图3 钢针对泥饼的作用示意图

2.2 泥饼模型的建立

利用ABAQUS力学软件建立泥饼的模型，如图4所示。模型各项参数与实际泥饼的各项参数相同：泥饼直径64 mm，厚度2 mm，在泥饼底部施加约束。

图4 泥饼模型

泥饼固化程度测试中，钢针对泥饼的破坏实际上是钢针在泥饼上1 mm圆形范围内施加一个分布应力，随着该压强的增加，当泥饼所受最大应力超过其屈服应力时泥饼发生破坏。基于此，在所建模型中对泥饼中心1 mm圆形范围施加一个压强并进行力学分析。

2.3 泥饼正向应力与抗压强度的转化

基于以上所建模型，输入通过自制设备测出的突破极限作用力和通过室内超声测量装置测得的物性参数，通过数值模拟得出泥饼受到正向作用力作用后的受力云图(见图5)。观察图5可以看出，泥饼只在中心区域的附近受到应力作用。在受力云图上设置由泥饼受力中心至泥饼受力为0处任意一点的直线路径，对该路径上的应力数据通过曲线的形式导出(见图6)，即可获得泥饼破坏的最大Mises应力(曲线最高点对应的Mises应力)。该模型需输入的参数共有3个：作用力、弹性模量和泊松比。因此需要对固化泥饼的真实弹性模量和泊松比进行测试。

图5 泥饼受力云图

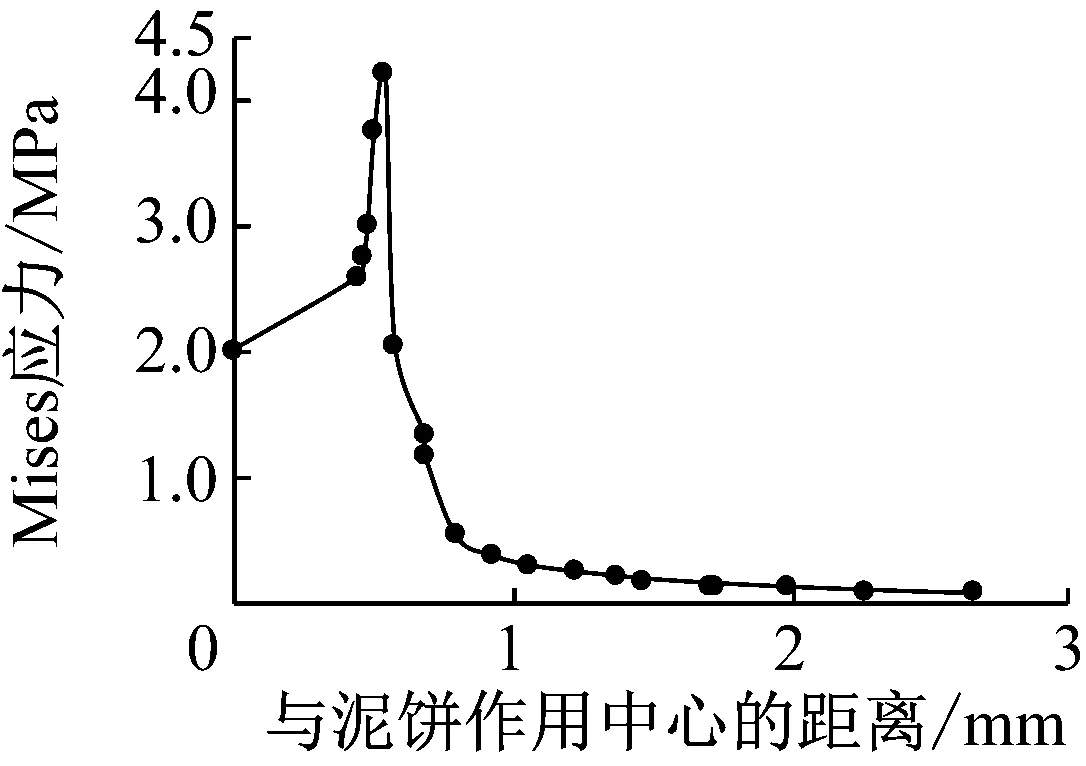
图6 某路径上的泥饼应力曲线

2.4 泥饼自身弹性模量及泊松比的测定

固化泥饼不同于普通的硬脆性材料，由于泥饼中含有较多的有机聚合物添加剂成分，并且泥饼含水率要远高于普通水泥基材料，造成泥饼的弹性模量远低于普通水泥基材料，而泊松比则要大很多。笔者采用超声测量装置对几种钻井液体系形成的固化泥饼进行了纵横波速测量，如图7所示。该系统由Olympus 5058PR高压超声脉冲发生器接收器和基于Labview的NI PXIe-1071数据采集仪组成。

纵波探头选用Olympus V101-RB，横波探头选用Olympus V150-RB，并通过下式计算得到了几种钻井液体系固化泥饼的弹性模量和泊松比(结果见表1)：

(1)

(2)

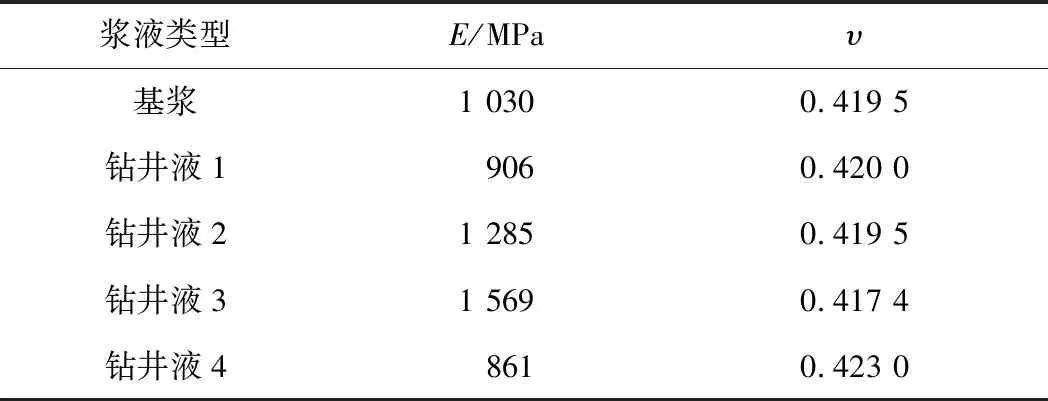
表1 不同钻井液泥饼的弹性模量和泊松比

式中：E为弹性模量，GPa；ρ为实验对象密度，kg/m3；vP为纵波速度，m/s；vS为横波速度，m/s；υ为泊松比。

2.5 泥饼抗压强度的计算

基于以上所建模型，通过模拟研究了突破力、弹性模量和泊松比与泥饼的最大Mises应力的关系。模拟过程中，分别保持上述3个因素中2个因素不变进行单因素分析(在测定的几种钻井液固化泥饼的弹性模量和泊松比范围内)，计算泥饼破坏的最大Mises应力。图8所示为针刺部位放大100倍的变形，通过数值模拟的变形图可以看出与实验得到的变形图(见图3)的变形非常吻合。模拟计算弹性模量和泊松比等参数对泥饼受到的最大Mises应力之间的关系如图9和10所示。由图9可以看出，不同泥饼弹性模量的变化对泥饼强度基本没有影响，即弹性模量对泥饼强度的影响基本可以忽略；由图10可以看出，泥饼泊松比的变化对泥饼强度有一定影响，但是不同泥饼的泊松比差别很小(见表1)，其影响也可以忽略。

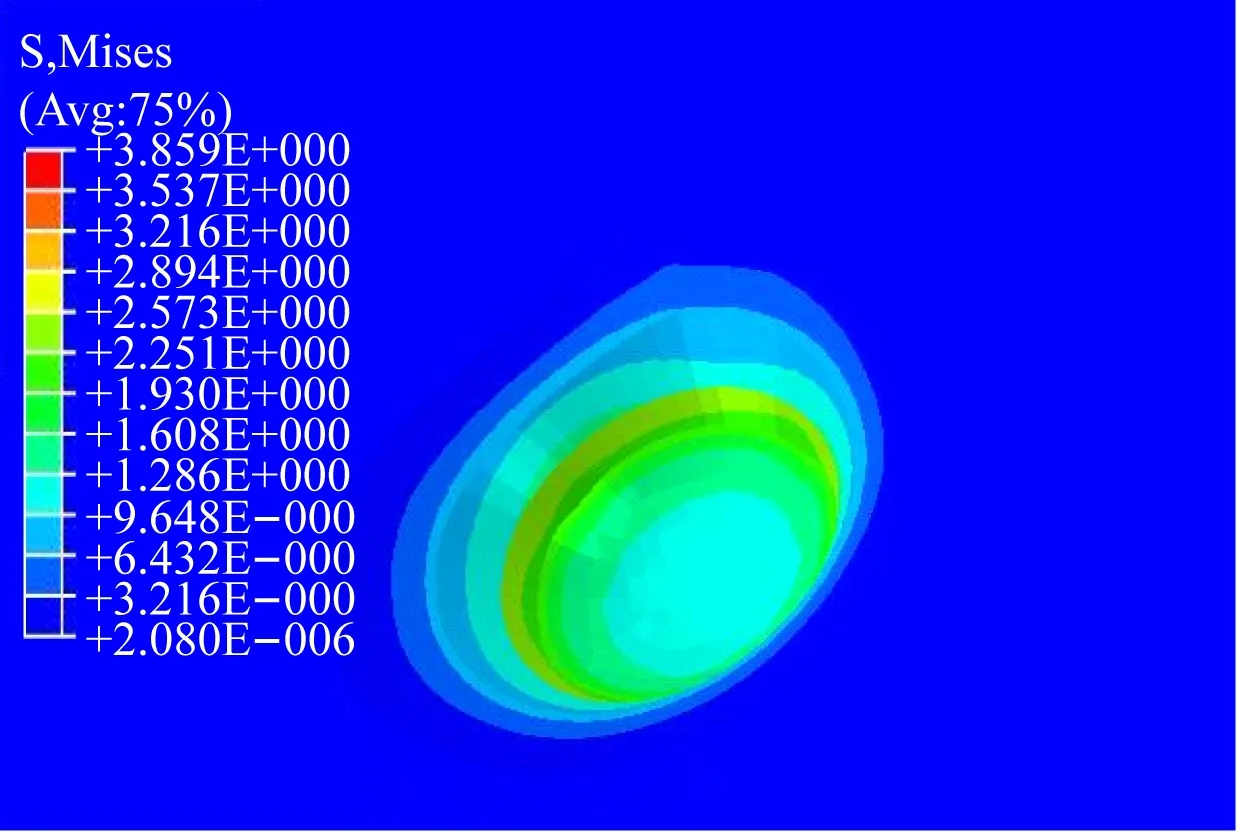
图8 针刺部位放大100倍变形(算例钻井液4)

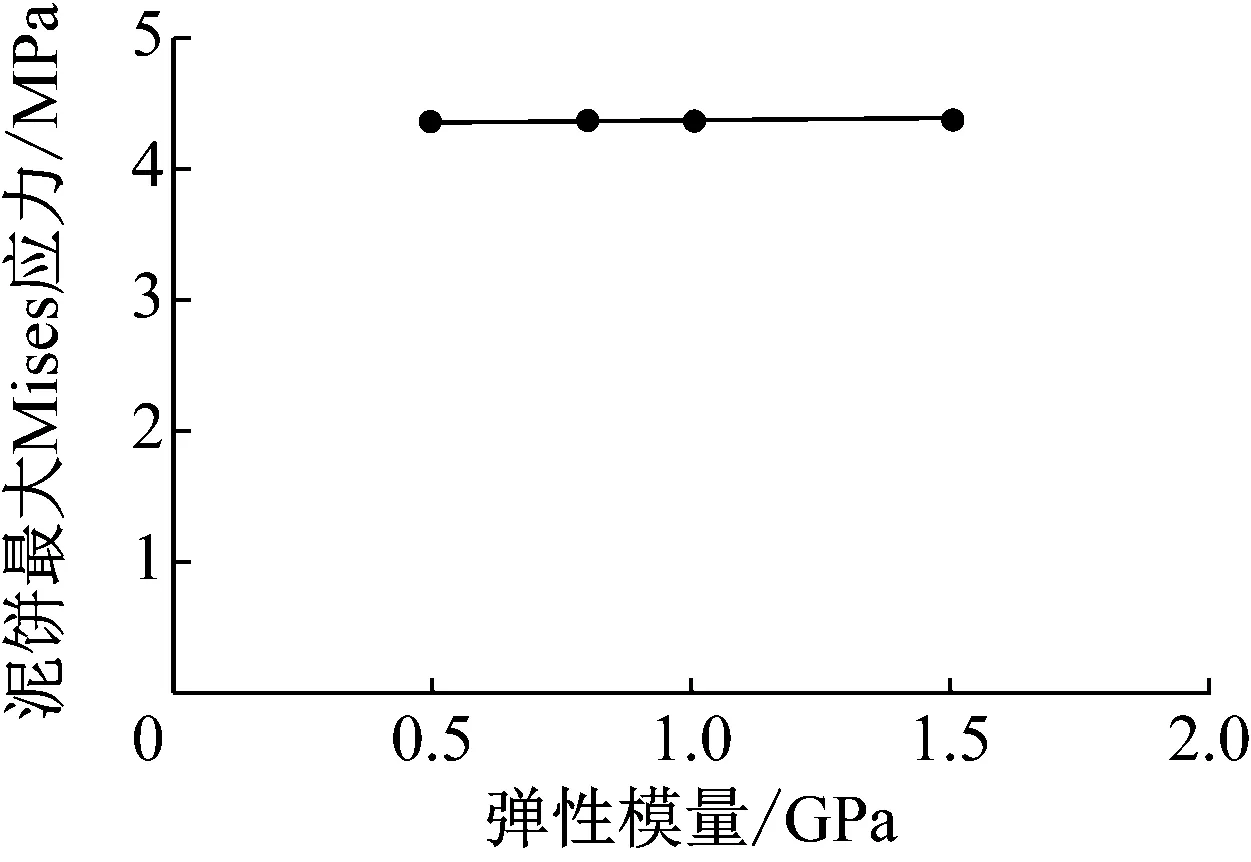
图9 泥饼最大Mises应力与弹性模量的关系

图10 泥饼最大Mises应力与泊松比的关系

模拟计算不同钻井液的固化泥饼破坏的最大Mises应力计算抗压强度数据及采用自制评价装置实验得到的针刺极限突破力如表2所示。将所得数据绘制成针刺突破极限作用力与抗压强度的关系图(见图11)，并将数据进行线性拟合，发现泥饼的计算抗压强度与针刺突破极限作用力具有良好的线性关系，因此可得出：

S=0.624 9F-0.007 9

(3)

式中:S为固化泥饼强度，MPa；F为固化泥饼极限突破力，N。

综上所述，对于本文研究的钻井液基浆和4种钻井液体系，固化泥饼强度主要与实验测定的极限突破力的大小有关，弹性模量和泊松比的影响可以忽略。因此，可以采用针刺测定固化泥饼极限突破力的方法，将实验得到数值代入式(3)进行力学值和强度值的转换，即可得到固化泥饼的强度值。

表2 不同钻井液泥饼的计算抗压强度

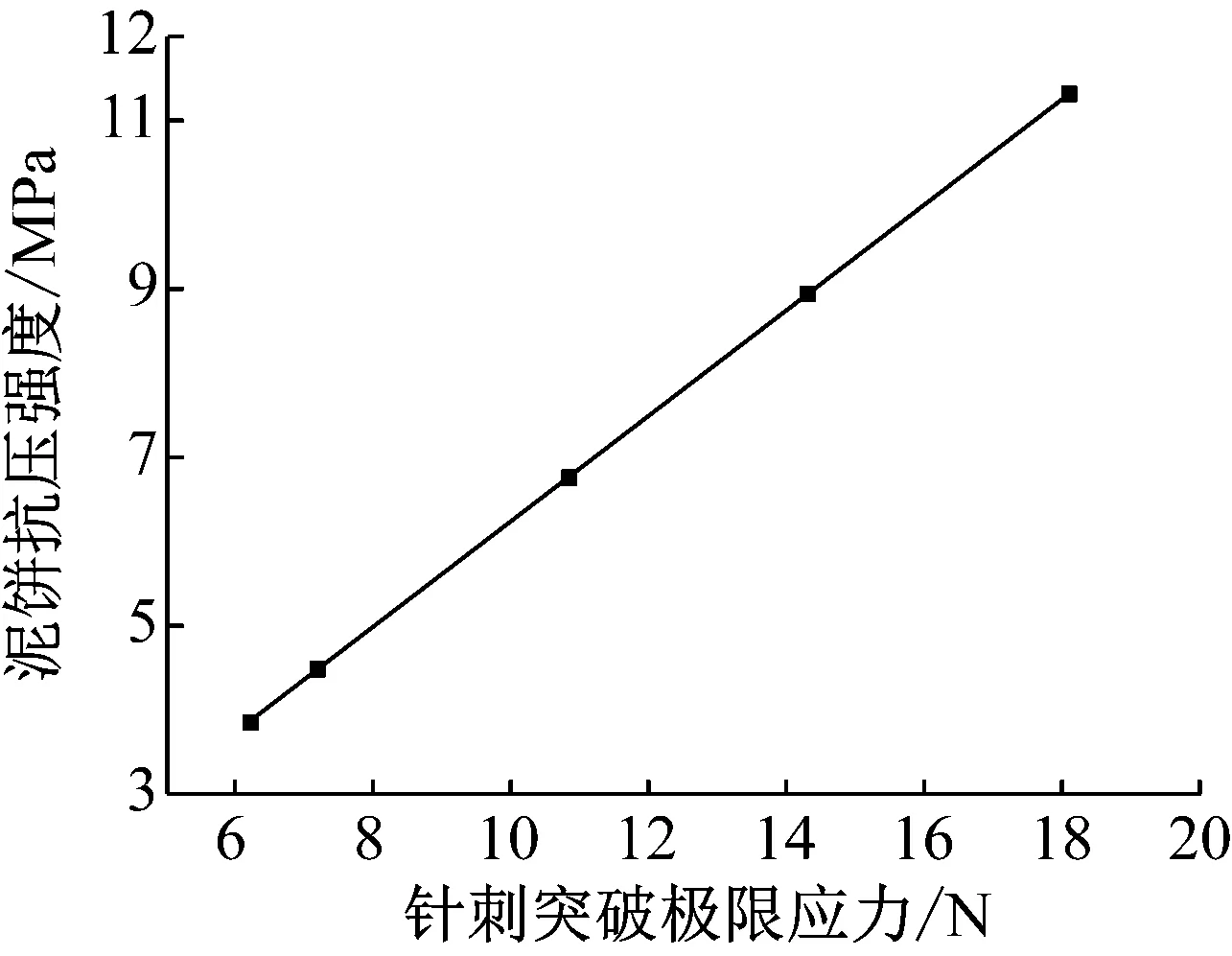
图11 泥饼针刺突破极限作用力与泥饼强度的关系

表3 泥饼抗压强度计算结果验证 MPa

3 泥饼抗压强度计算结果验证

为了对泥饼抗压强度的计算结果进行验证，对泥饼的剪切胶结强度与液压作用下固化泥饼被突破的压力进行了测试，结果如表3所示。结果表明，泥饼的计算抗压强度与其剪切胶结强度以及突破压力有很好的吻合性，当计算抗压强度大时，其剪切胶结强度与突破压力也相应增大。因此，综上所述，固化泥饼的抗压强度可以通过对固化泥饼针刺极限突破力的测量及式(3)的计算得到。

4 结 语

本文针对目前泥饼固化技术研究中泥饼强度评价方法欠缺的问题，提出了固化泥饼的强度测试和评价方法，该方法利用自制简易装置测试泥饼固化程度，并通过建模分析泥饼所受极限力与泥饼强度的关系。实验证明，泥饼固化强度与泥饼承受的针刺突破极限应力具有良好的线性相关性，通过拟合公式计算得到的强度与泥饼的剪切胶结强度与突破压力具有较好的吻合性。该方法能够定量描述泥饼的固化强度，简单易行，对于泥饼固化技术的实验室评价具有重要的意义。