纯电动汽车电驱动系统扭转振动特性分析

王 欢， 吴 斌， 张苏旭， 陈存玺

(北京工业大学 环境与能源工程学院， 北京 100124)

文献[3-6]均通过对传动系统各部件进行简化建模，再对振动模型仿真分析来研究振动特性，但在建模时没有考虑到电动汽车中存在的机电耦合问题。文献[7]建立了考虑电机转子偏心影响的机电耦合振动模型，通过对该非线性振动模型求解展示了丰富的动力学现象。文献[8]通过试验验证了电机转矩波动是引起传动系统振动的主要原因之一，文献[9]建立了一种可以反映电机电磁转矩的解析模型，从而揭示了永磁同步电机电磁振动的频率特征。文献[10-13]在电动汽车的扭转分析中考虑了机电耦合引起的电磁刚度，并对电磁刚度的状态进行了详细的研究，证明了在建模时考虑机电耦合因素可以对系统的振动得到更深入的了解。这些文献的机电耦合动力学模型中的参数如电磁刚度，是由理论计算确定的，但其计算过程中的机电参数过多，且有部分数据不明确只能做近似选取，因此计算得到的数据和实际存在偏差，且实际的机电参数受工况影响具有不确定性。

目前对机电耦合所引发的振动问题进行研究的论文大部分都是理论和仿真，通过试验与仿真相结合的手段来探究机电耦合所引发的振动现象的论文却鲜有报道。本文以某电动汽车为研究对象，主要针对其在中低速行驶时所发生的低频扭振现象进行研究，通过建立带电磁刚度的电驱动系统传动模型，进行振动台架试验来验证模型的准确性，并针对模型中电磁刚度的不确定性进行试验以获取其数值。

1 电驱动系统扭振建模

1.1 电驱动系统模型简化

某纯电动汽车电驱动系统包括电机、变速器、左右半轴和车轮等。如图1所示，驱动电机为整车提供动力，驱动力通过两挡变速器、减/差速器总成的速比转换，再经由左右半轴传递到车轮，从而驱动汽车行驶，其中两挡变速器通过同步器换挡。由于在汽车结构中，除了含有主动阻尼的结构，如减振器，一般结构的阻尼比远小于10%，其阻尼对固有频率的影响不大，因此在对电驱动系统建模时，可忽略阻尼的影响[14]，将电动汽车传动系统看作是一个复杂的由惯量-刚度所构成的多自由度系统，通过对该惯量-刚度系统进行模态分析，可以得到电驱动系统的振动特性。

图1 某电动汽车传动系统简图

在针对电动汽车的低频扭振现象进行建模时，可根据简化原则用集中质量法将电机、变速器、半轴和车轮等各传动部件进行合并简化[15-16]，将电驱动系统简化为两自由度模型可以得到传动系统的振动模态[17]。根据传动系统的动力传输路径，电驱动系统可分为输入和输出端，其中驱动电机、输入轴、一档主动齿轮、二挡主/从动齿轮可简化为输入端，而一挡从动齿轮、主减速器主/从动齿轮、差速器、整车惯量简化为输入端，输入端和输出端之间用一等效弹簧来模拟连接轴的扭转刚度。考虑到在电机的驱动转矩中有一扰动项为kφ[13]，其中k为电磁刚度，与扭转刚度的单位相同，均为N·m/rad，因此在建模时可将其看作一个变刚度弹簧，连接在输入端惯量的前端，用来模拟机电耦合的作用。在振动系统建模时忽略系统阻尼的影响，最终模型图如图2所示。

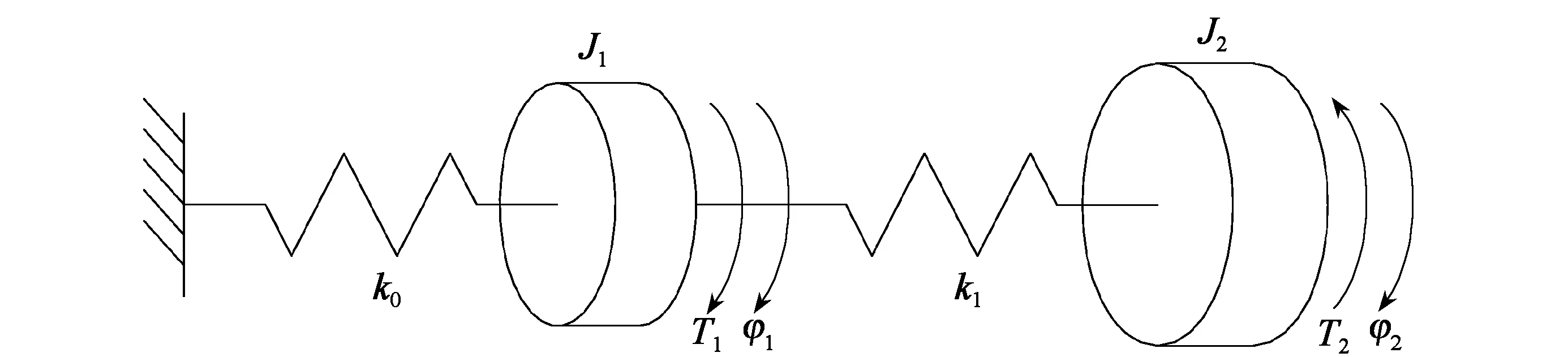
图2 带电磁刚度的两自由度模型

其动力学方程为

(1)

其中k0为电磁刚度，k1为等效连接轴刚度，J1为输入端等效惯量，J2为输出端等效惯量，T1为驱动转矩，T2为负载阻力矩，φ1为输入端的扭转角，φ2为输出端的扭转角。当不考虑外界激励时，可由式(1)得到该系统在自由振动时的频率方程为

田贤忠 男，1968年生于浙江杭州，博士，现为浙江工业大学计算机学院教授，当前的研究方向包括能量捕获无线传感器网络、网络编码、移动计算、无线网络协议优化等.

ω4-(a+c)ω2+(ac-bc)=0，

(2)

其中a=(k0+k1)/J1，b=k1/J1，c=k1/J2。

此时系统的固有频率值可由式(2)得到：

(3)

若不考虑电磁刚度，则此时系统的固有频率为

(4)

1.2 电驱动系统模型参数确定

在对电驱动系统初步简化时，根据集中质量法，将各部件质量等效到其中心轴上，得到各个部件的转动惯量，表1为电驱动系统各部件的转动惯量值。再通过速比对传动系统各部件进一步简化，划分为输入端和输出端，其中一挡速比i1=3，二挡速比i2=1.194，主减速器速比i0=3.905。

表1 电驱动系统扭振参数

在一挡挡位下输入端等效惯量为

(5)

输出端等效惯量为

(6)

表2为经过式(5)、(6)等效计算得到的一挡时的两自由度模型参数，由式(4)和表2中的参数可得系统在不考虑机电耦合时的固有频率为5.97 Hz。

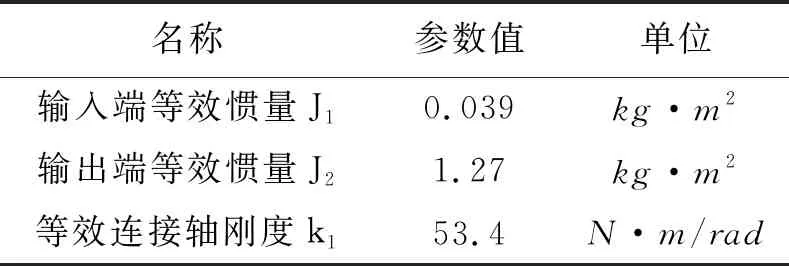
表2 两自由度模型参数

电磁刚度k0，则可根据其定义式(7)可知，电磁刚度与电机转矩相关：

k0=∂T1/∂φ。

(7)

由于电机电磁转矩T1受电机运行工况的影响，随工况而发生变化，因此电磁刚度的具体数值无法直接计算得出，本文将通过后续试验来确定电磁刚度的具体数值和变化规律。

2 电驱动系统稳态扫频振动试验

2.1 试验目的

为获取系统的固有频率，对电驱动系统进行稳态扫频激励试验，改变电机转矩波动频率，加大转矩波动幅值，以便于测出传动系统的固有频率。当系统固有频率和扫频激励频率发生共振时，其振幅较大，即可通过对采集到的转速信号进行分析来获取固有频率。对试验采集的数据进行分析处理以便于验证两自由度模型的准确性，并得到电磁刚度在不同工况下的变化规律。

2.2 试验系统

试验系统包括整车试验台架、振动试验测试设备和驱动电机控制部分。整车试验台架由永磁同步电机、2AMT、半轴、车轮、飞轮、制动器组成，各部件惯量参数与表1一致。如图3所示，驱动电机为永磁同步电机，作为机械动力输入，通过2AMT、减/差速器中的齿轮传动以及左右半轴向车轮传递动力。飞轮压在车轮上模拟整车重量，制动器连接在飞轮上，通过对飞轮施加负载来模拟行驶过程中的整车阻力矩，达到模拟整车的目的，车轮转速即为整车车速。

振动试验测试设备包括试验台架、速度传感器和振动测试系统LMS_Test.Lab。如图3虚线框①内所示，转速传感器分别安置在电机、车轮及飞轮上，LMS_Test.Lab振动测试系统用来采集并分析电驱动系统在试验所测得的振动信号。

对驱动电机进行转矩控制的模型如图3虚线框②内所示，通过对电机控制器MCU发送控制字和需求转矩值实现对驱动电机的控制。整车控制器VCU通过CAN向电机控制器MCU发送控制字及需求转矩，并通过CAN接收电机状态，如电机转速、电机温度、控制器温度、电流等。

图3 整车振动试验台架示意图

2.3 稳态扫频振动试验方案

以2AMT挡位在一挡时进行试验，此时电机到车轮的速比为11.71，车轮到飞轮的速比为0.85。为分析电磁刚度引起的低频振动，稳态试验采用低速工况。从电机转速200 r/min开始，每隔200 r/min测量一次，直至电机转速到达1000 r/min。试验时保持电机转矩为一恒定值，通过对电机转矩进行控制，改变电机电磁转矩波动的频率和幅值，使得电机转矩波动频率从0开始以0.01 Hz为步长持续增长，直至频率到达10 Hz，试验时采集各测点转速信号，以供分析传动系统振动响应情况。为研究在不同输出转矩下电磁刚度的变化，电机通过输出不同的转矩并使转速维持在相同值，采集在不同转矩下的转速信号进行频率分析，为方便对比，维持各转速的电机输出转矩均以10、15、20、25 N·m这4种情况进行试验。

3 试验结果分析

3.1 稳态扫频试验结果

以电机转速维持在1070 r/min稳态时为例，分析振动试验结果。在LMS中将采集到的电机转速信号做FFT处理，得到频域图。为更直观地观察低频振动，将处理过的频域图横坐标设为对数坐标分布。通过对电机、车轮、飞轮端采集的数据进行分析比对，发现具有相似性，因此在后续分析中将统一采用电机端采集的数据进行分析。图4为经LMS处理过后的电机端频域图，从图中可知主要振动频率有0.13、6.02、17.95 Hz，其中0.13 Hz为电磁刚度引起的一阶低频振动，6.02 Hz左右为传动系统的二阶固有频率，这与不考虑机电耦合时的固有频率5.97 Hz相比略微增大，是受电磁刚度的影响，而17.95 Hz则是电机转速在1070 r/min时的自身转频。试验测得的二阶固有频率与不考虑电磁刚度时的两自由度模型频率相接近，验证了模型的准确性，但是在计算结果中漏掉了0.13 Hz的低阶频率，而由式(3)可知，带电磁刚度的模型能够得到两阶固有频率，较符合试验结果，能更精准地得到系统的振动形态。

图4 稳态扫频试验电机转速频域图

汇总各工况下的所有试验结果，通过分析电机端频域图可知，该电驱动系统在本文试验工况下的主要振动频率基本有3个：电磁刚度引起的一阶固有频率、传动系统二阶固有频率和电机对应转速下的自身机械转频。为研究在不同电机转速下，电机转矩波动所产生的电磁刚度对一阶固有频率的影响，现将所有试验得到的一阶固有频率值汇总于表3。由表3可知，一阶固有频率值大多为0.13 Hz，少数工况下虽频率值略有不同，但也始终在0.1～0.2 Hz之间波动。且通过稳态扫频试验结果汇总可知，台架试验中电机电磁转矩波动的频率与幅值对一阶固有频率影响不超过0.1 Hz，频率值相对较低。

表3 不同工况下一阶固有频率汇总

3.2 电磁刚度值计算

通过稳态扫频试验得到的一阶固有频率值ω1，可由动力学方程(1)式得到电磁刚度k0，计算方程为

(8)

式中d=J1/J2。

根据式(8)和表3汇总的一阶固有频率，可推出在本文试验各工况下的电磁刚度值如表4所示。在汽车低速稳态运行时，电磁刚度值始终在0.52～2.14 N·m/rad范围内。

表4 不同工况下电磁刚度值汇总

3.3 固有模态分析

由表4可知电磁刚度虽然在不同工况下会有一定程度的变化，但其值基本保持在0.52～2.14 N·m/rad之间。根据表4中的电磁刚度值，可由式(4)得到系统的固有频率随电磁刚度的变化关系。如图5所示，随电磁刚度的增大，系统的两个固有频率均有不同程度的上升。此时系统在两个频率下，输出端和输入端的振幅比可由下式得到：

图5 固有频率随电磁刚度变化关系图

(9)

(10)

则此时一、二阶的振型分别为(1，r1)和(1，r2)。当电磁刚度分别为0.52、0.89、1.53、2.14 N·m/rad时系统的两阶振型图如图6所示，系统在一阶固有频率下，输入输出端同向运动，而在二阶模态下，输入输出端则呈现相反的运动状态。且随着电磁刚度的增加，在一阶模态下，输入输出端的振幅比逐渐增加，而在二阶模态下，其振幅比的绝对值则逐渐减小。

(a) 一阶固有频率振型图 (b) 二阶固有频率振型图

4 结论

(1)通过对电驱动系统进行稳态扫频激励实验，得到了系统的两个固有频率，验证了建模时考虑机电耦合能够更准确地得到系统的振动形态。

(2)通过台架试验可知，某纯电动汽车在本文试验的中低速稳态工况下，主要振动响应包括低阶固有频率和汽车部件自身机械转频。在以后的减振研究中可通过传动系统的模型参数优化，改变固有频率值，以避免转频与固有频率相同时产生共振。

(3)由电磁刚度引起的低频振动，在本文的试验的中低速工况下，基本保持在0.1～0.2 Hz，频率较低，而电磁刚度值在不同的试验工况下也基本在0.52～2.14 N·m/rad范围内波动，可以作为后续建模仿真参数选取的参考依据。

(4)系统的两阶固有频率会随电磁刚度的增大而有不同程度的上升，且随着电磁刚度的增大，一阶频率下的振幅比逐渐增加，二阶频率下的振幅比绝对值则逐渐减小。