关键节点和平滑处理的PRM路径优化方法

魏念巍，姜媛媛，刘延彬，辛元芳，洪 炎

安徽理工大学 电气与信息工程学院，安徽 淮南 232001

1 引言

路径规划是机器人研究领域的一项基础并且关键的技术。路径规划技术迅速发展，研究人员提出诸如单元分解法、快速搜索随机树（Rapidly Exploring Random Tree，RRT）法[1]、人工势场法[2]、概率路图（Probabilistic Roadmap，PRM）[3]法等各种路径规划算法[4]。一些传统的规划算法需要对图中的障碍物进行建模确定其位置，计算难度及规划路径变得复杂。基于采样的PRM算法可以在含有障碍物的地图中规避障碍物，并在自由空间内规划路径，降低了计算难度。基于采样的规划方法不仅应用在各种机器人的路径规划方面[5]，在建筑物疏散路径规划、分支管路自动布局[6]、计算机动画、生物学等其他领域也被运用[7]。

为了提高PRM 算法中路线图的连通性，Huang 和Gupta提出应用Delaunay三角剖分特性的临近点选择策略[8]。Mali提出使用多重样本节点以及节点和地图路线的有效性等特征提高PRM 的表现力[9]。Janson 等人提出使用某种确定性采样序列替代随机性采样序列实现PRM路径的渐进最优[10]。

采用基本PRM算法进行路径规划所形成的路径含有的拐点过多，在需大幅转向的位置路径不够平滑。机器人在路径的拐点处需要调整姿态完成转向，过多地调整姿态会使得整体的行驶时间加长，整体行驶性能下降[11]。初始路径不够平滑使得部分路径不能遵循机器人的行驶规律，使得路径不能确定可行。在此问题的基础上提出使用D-P算法提取PRM初始路径节点中的关键节点，以降低机器人调整姿态的次数，从而降低行驶时间。基本的D-P 算法对复杂曲线简化时易产生自相交等错误，阈值的选取对最终简化结果有较大影响，阈值过大会导致局部区域失真，阈值过小不能有效化简曲线。刘波等人提出基于单调链与二分法的D-P 改进方法解决压缩复杂曲线时的自相交问题[12]。Zhai 等人将D-P 算法与多路树模型相结合用于简化线性特征质量评估，无需设置 D-P 算法的阈值[13]。Zhao 和 Shi 考虑D-P算法阈值可变性，根据船舶尺寸和水域情况选择阈值实现对船舶轨迹的压缩[14]。路径的平滑处理使用Clothoid曲线进行拟合。Clothoid曲线是一种曲率连续的平面参数曲线，可使拟合曲线连续、平滑[15]，最初在道路以及桥梁的设计中应用较多，后来被应用于机床加工[16]、无人机航行轨迹[17]等方面。

2 基本PRM算法

PRM 算法是一种基于图搜索的方法，基本的PRM算法包括学习阶段和查询阶段。学习阶段主要是构建路径网络图，首先在给定地图的自由空间(Cfree)中随机撒点，然后通过局部规划器连接节点，形成路径网络图。查询阶段是将给定的初始节点和目标节点与路径图相连接，并通过A*等搜索算法找到起始节点到目标节点的路径。

学习阶段构造路径网络图R(N,E)的过程如下：

算法1 PRM

1.N←NULL

2.E←NULL

3.loop

4.c←a randomly chosen free configuration

5.N←N∪{c}

6.Nc←a set of candidate neighbors ofcchosen fromN

7.for alln∈Nc, in order of increasingD(c,n) do

8.if (c,n) is not same connected component ofEand Δ(c,n)≠NIL then

9.E←E∪(c,n)

10.updateR(N,E)

R(N,E)为无向图，其中N为随机点的点集，E为所有可能两点连接的路径集。首先对R(N,E)初始化，N、E初始状态为空。然后在自由空间内随机撒点，每个随机点要确保机器人不与障碍物相碰撞。在点集N中选取ni作为ci的邻域点构成邻域点集Nc，邻域点的距离要在一定范围内，即Nc={n∈N|D(c,n)＜d}，d为设定的最大允许距离。使用局部规划器连接采样点c以及其邻域点n，生成一条无碰撞路径。如果连接线段与威胁体碰撞，则不能相连，即保持连接线段全部处于自由空间中。若经过碰撞检测，邻域点集Nc中存在节点n能与随机采样点c相连，将相应的连线作为图的边加入到对应的路线子图中。若新采样点与其邻近点集不存在直线段相连，则把该采样点作为一个新的子图存储。当采样点可以同时与多个子图连接时，被连接的子图就通过新采样点合并成一个子图。随着采样点的增多，不同的子图连接在一起，当所有子图连接成一张路线图并满足采样点密度等其他终止条件时，路径网络图构建完成。图1 为PRM 算法在学习阶段构建的路径网络图。

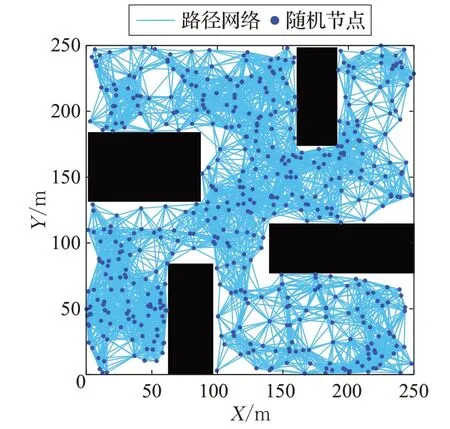
图1 路径网络图

在查询阶段将初始点s和目标点g与路径网络中的两个节点ci、cj分别连接，然后在无向路径网络中寻找ci与cj之间的路径，由此可构建s节点与g节点之间的路径。在学习阶段的关键在于如何寻找s到ci以及g到cj的路径，可以采用学习阶段的局部规划器的方法来寻找无碰撞路径。学习阶段寻找到的一条机器人路径如图2所示。

3 路径优化

PRM 算法在构建路径网络图时采用随机采样策略，采样点随机分布在自由空间Cfree中，在查询阶段搜索路径时依赖于采样点的分布。若在构建网络图时选择的采样点过少，则随机采样策略不能保证采样点覆盖整个自由空间，最终导致规划路径失败；若选取过多的采样点，则会增加算法的计算量，延长路径规划时间，路径节点个数会大量增加，最终形成的机器人路径包含的拐点过多。虽然研究人员提出了在构建路径网络图时的改进方法，如在自由空间内采样时用均匀采样代替随机采样以保证采样点均匀分布在整个自由空间，或采用高斯采样或桥测试等方法增强在障碍物周围的连通性，提高计算效率。但为了保证路径规划成功，并不能选取过少的采样点，故规划路径仍存在拐点过多的问题。由于机器人需在拐点处调整姿态转向，这使得机器人整体行驶时间加长。由于规划所得的路径为在路径网络图中两节点间的最短路径，路径中存在的斜线多，一些拐角过陡。路径的曲率突然改变，会影响到机器人的整体行驶性能和效率。机器人不能急转弯，需要一定的角度才能完成转向，初始路径包含一些机器人无法遵循的急转弯。针对这一问题，提出一种路径优化方法，使用D-P算法以及Clothoid 曲线提取路径关键节点并进行平滑处理。优化过程如图3所示。

图2 PRM路径

图3 路径优化过程

在一给定障碍地图中，首先使用PRM 算法进行路径规划，构建自由空间内的路径网络图，然后通过查询阶段得到一条从起始点到目标点的初始机器人路径。对于初始路径中的路径节点使用D-P 算法提取其中的关键节点，连接路径关键节点形成的是含有较少拐点的优化路径。使用Clothoid 曲线进行拟合可以得到最终的比较平滑的机器人路径。

3.1 关键节点的提取

在PRM算法形成的初始路径中，路径节点过多，机器人在拐点处需要调整姿态转弯，拐点过多使得路径过长，机器人行驶时间加长。提取路径节点中的关键节点进行路径优化可以有效减少路径的总长以及机器人行驶时间。

算法2 D-P算法

1.Function DP=D-P_original({N1,N2,…,Nn},φ)

2.DP=NULL

2.Fit a linel withN1andNn

4.D←{d1,d2,…,dn} //求各节点{N1,N2,…,Nn}到基准线l的距离{d1,d2,…,dn}

5.for alldi∈Ddo

6.dmax←max{d1,d2,…,dn} and pointNmaxcorresponding todmax

7.ifdmax≤φthen

8.DP←{DP,N1,Nn}

9.else

10.DP←{DP,D-P_max(N1,Nmax)} and DP←{DP,D-P_max(Nmax,Nn)}

11.end if

12.return DP

使用D-P算法提取路径关键节点的基本步骤如下：首先确定一阈值φ，连接初始路径节点的初始点和目标点形成一条基准线。然后计算初始点和目标点之间所有节点到基准线的距离，得到距离基准线最远的节点。比较此距离与预先给定的阈值φ的大小。如果小于φ，则该基准线段作为新的路径，该段路径处理完毕。如果距离大于给定的阈值φ，把此节点纳入关键节点集，该关键节点分别与初始点和目标点相连接形成两条新的基准线，并对这两段基准线重复上面步骤提取新的关键节点。最后可以得到关键节点集，依次连接关键节点，即可得到新的优化路径。阈值的选取对路径优化的影响很大，阈值过大虽然会有效减少拐点个数，但无法确保优化路径可行性；阈值过小不能有效减少路径中拐点的个数。故需根据地图障碍物的分布情况以及初始路径节点个数来确定D-P算法的阈值，在含有较多障碍物的复杂地图中，选取较小的阈值有助于保证优化路径成功可行；在含较少障碍物或障碍物分布简单的地图中，可选择较大阈值提取路径节点中关键节点。

以图4 的路径为例，初始路径节点为A1～A8。设定一合适阈值，连接A1、A8，在A1和A8之间的路径节点中距离线段A1A8最远的节点为A3,A3与A1A8的距离为d，大于预先设定的阈值φ，把A3视为一个关键节点。分别连接A1、A3和A3、A8形成两条新的基准线段A1A3和A3A8。由图4（b）可以看出，在A1与A3之间与线段A1A3距离最远的路径节点为A2，在A3和A8之间距离线段A3A8最远的路径节点为A5，分别与阈值相比较，找出新的路径关键节点。依次重复下去可以得到路径关键节点集，连接路径关键节点即可得到图4（c）所示的新路径B1—B2—B3—B4。

图4 D-P算法提取路径关键节点

3.2 路径平滑处理

Clothoid曲线是一种参数平面螺旋曲线。该曲线的最大特点是：以弧长为参变量及曲率连续变化，并囊括直线与圆两种特例。Clothoid曲线的曲率变化与曲线的弧长成正比，Clothoid曲线表达式如式（1）：

式中，(x0,y0)为初始点，θ0表示初始切线角，k0为初始曲率，c表示曲率锐度的参数，s表示曲线的弧长。Clothoid曲线的曲率k以及切线角可以表示为式（2）：

Clothoid曲线大多应用在根据已知的一系列离散坐标点，在特定的条件下生成曲率连续变化的曲线。若设D-P算法提取的关键节点是坐标为P(xi,yi)(i=1,2,…,k)的一组离散点，那么使用Clothoid 曲线进行拟合，就是在曲率连续的条件下求解上述k个离散点的各Clothoid曲线段。对一组离散点用Clothoid 曲线进行拟合形成的曲线如图5所示。

对于其中第l段Clothoid 曲线来说，其两端端点坐标为(xl,yl)、(xl+1,yl+1)，由式（1）可知两点应满足下列条件：

图5 一组离散点和Clothoid曲线

其中，sl为第l个Clothoid曲线段的弧长，θ0l以及k0l分别表示(xl,yl)点处的切线角和曲率。为了保证在各个点处的曲率连续性和曲线平滑性，(xl+1,yl+1)作为第l段Clothoid曲线的终点以及第l+1 段Clothoid曲线的起点，此处各参数应当满足：

式中，θ0l+1、k0l+1分别表示第l+1 段Clothoid曲线的初始切线角和初始曲率，分别与第l段Clothoid 曲线在(xl+1,yl+1)处的切线角θl以及曲率kl相等。即在两段Clothoid曲线的连接处的切线角和曲率的大小不变。

4 仿真结果

使用Matlab进行仿真，在如图6所示的含障碍物的250 m×250 m大小的地图中，设定机器人的起始点坐标为（10，240），机器人的目标点坐标为（240，10）。选择随机点的个数为500，使用基本PRM方法进行路径规划得到的初始机器人路径如图6 所示。图中的节点为机器人路径的路径节点，连线为初始路径。

图6 PRM路径规划的初始路径

由图6可以看出，经基本PRM方法进行路径规划得到的初始路径共有14 个路径节点，在此基础上进行路径优化，选择D-P算法的阈值为4，提取路径节点中的关键节点，并使用Clothoid 曲线对路径关键节点进行拟合，得到最终较为平滑的新路径如图7所示。图中点划线路径为初始路径，星点为经D-P算法提取的路径节点中的关键节点，虚线为关键节点组成的新路径，实线路径为经Clothoid曲线平滑处理过后的平滑优化路径。

图7 经优化后的平滑路径

由图7 可知，经D-P 算法提取路径节点中的关键节点，路径节点由原先的14 个缩减为5 个关键节点，有效减少了机器人路径中拐点的个数，经Clothoid曲线平滑处理后的最终路径与初始路径相比更加平滑。

在图8所示的较为复杂的250 m×250 m大小的障碍地图中，选择机器人的起始点坐标为（10，10），目标点坐标选为（10，120），由PRM 方法进行路径规划后得到的初始路径如图8所示。

图8 较复杂地图PRM路径规划的初始路径

由图8 可以看出，机器人路径共有27 个路径节点，经过圆形障碍物时需大幅转向行驶。初始路径在此处的拐角过陡，有突出棱角，机器人需在拐点处调整姿态来完成转向，路径不够平滑，使得机器人的行驶时间加长。选择D-P 算法的阈值为4，提取路径节点中的关键节点，再经平滑处理后的最终路径如图9所示。

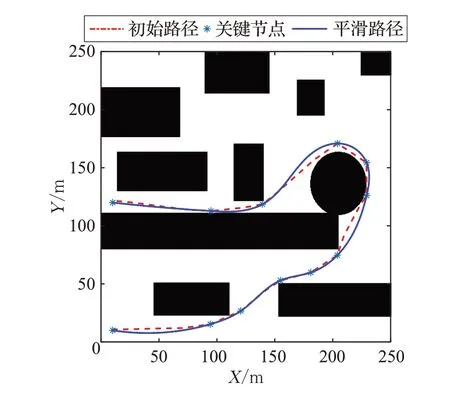
图9 较复杂地图经优化后的平滑路径

由图9可知，优化后的平滑路径的路径节点由原先的27 个减少为12 个，有效减少了机器人行驶过程中的拐点个数。在圆形障碍物处的机器人路径变得更加平滑，无较突出的棱角。经过优化后的最终路径整体比较平滑，能有效减少机器人的行驶时间，并提高机器人的整体行驶性能。

在图10 的障碍地图中，设机器人初始点坐标为（10，10），目标点坐标为（10，240），机器人行驶路径较复杂。使用基本的PRM方法进行路径规划得到的初始路径如图10所示。

图10 复杂路径经PRM路径规划的初始路径

初始路径中的路径节点为23 个，由于路径较为复杂，初始路径含有较多的尖锐拐角，有较多的急转弯，这使得机器人在行驶过程中需要经常大幅度调整姿态形成转向，机器人的整体行驶时间加长。选择D-P算法的阈值为3，提取路径关键节点，Clothoid曲线进行平滑处理得到的平滑路径如图11所示。

经优化后的最终路径的路径节点的个数由23个减为14 个。最终路径与初始路径相比，在较为尖锐的拐角处更加平滑，能够有效减少机器人在拐角处调整姿态所需的时间。经优化处理后的最终路径与初始路径相比，拐点个数明显减少，平滑性明显提高，可以有效降低机器人的整体行驶时间。

表1 PRM初始路径和优化平滑路径实验数据比较

图11 复杂路径经优化后的平滑路径

由表1可以看出，相较于基本PRM规划路径形成的初始路径，经优化后的最终平滑路径的路径节点个数以及路径转折次数明显减少，相应地机器人的拐点个数也会降低。与简单障碍地图相比，较复杂的障碍地图以及复杂路径障碍地图中初始PRM路径节点以及路径转折次数较多，经优化处理后的平滑路径可以有效降低机器人拐点的个数。

5 结束语

移动机器人路径规划使用基本PRM算法生成的初始路径中拐点个数过多，采用D-P算法提取初始路径节点中的关键节点，从而减少机器人行驶路径拐点的个数。针对路径部分拐角过陡和路径不够平滑的问题，使用Clothoid曲线平滑路径。仿真结果表明，在复杂路径或复杂障碍地图情况下该优化方法都可有效减少路径中拐点的个数并使路径更加平滑。