基于贪心策略的最近邻Top-k 偏好查询方法

蔡 盼，李 昕，孟祥福，褚治广

辽宁工业大学 电子与信息工程学院，辽宁 锦州 121001

1 引言

现有的空间关键字查询技术大多以用户为中心，返回与用户位置邻近、文本相关的兴趣对象。然而，用户希望得到的查询结果不仅要考虑查询结果的位置相近性和文本相关性，还要考虑周围的基础设施属性。比如，用户想要租赁房屋，要求距离房屋500 m 的范围内存在公交站。此类查询被定义为Top-k空间关键字偏好查询，其中兴趣对象（房屋）周围的基础设施（公交站）称为特征对象。与传统的空间关键字查询相比，Top-k空间关键字偏好查询关注兴趣对象周围的特征对象对于用户要求的满足程度。查询需要考虑兴趣对象与特征对象之间的空间关系以及特征对象与用户查询关键字的文本相似关系，这使得Top-k空间关键字偏好查询更具有挑战性。

已有的Top-k空间关键字偏好查询包含范围约束、最近邻约束和影响区域约束三种类型的查询方式。给定一个查询范围r，范围约束根据距离兴趣对象范围r内的特征对象对兴趣对象进行评分；最近邻约束是以距离兴趣对象最近的特征对象为依据对兴趣对象进行评分。上述两种查询方式侧重于考虑特征对象与兴趣对象之间的位置邻近，然而这种方式可能会导致查找到的目标对象仅从空间上满足用户要求，而在文本上与用户查询关键字的相关度较低。第三种查询方式检索全部空间区域，查找距离与用户查询关键字最相关的特征对象的最近兴趣对象作为候选结果，这种查询方式有效地避免了查询结果的遗漏以及与用户关键字要求不匹配的情况。然而，由于影响区域约束需要检索全部空间区域，在大数据量情况下会导致较低的查询效率。

针对上述问题，本文研究了影响区域约束的Top-k空间关键字偏好查询解决方法，在此基础上提出了一种改进算法，主要贡献如下：

（1）提出了一种有效的剪枝策略，利用贪心思想和最近邻思想，每次查询选择最好的候选对象，有效解决了查询效率低的问题。

（2）基于剪枝策略提出了一种查询改进算法——GS-NNA（Greedy Strategy based Nearest Neighbor Algorithm），能够获得满足用户查询需求和特征对象偏好的查询结果。

（3）进行了大量的实验验证，从查询关键字、查询结果数量以及数据集基数三方面评估GS-NNA 算法的性能，并与现有相关算法进行比较。实验结果表明，提出的GS-NNA 算法在查询响应时间上比现有相关算法快了一个数量级。

2 相关工作

本文工作涉及Top-k空间关键字查询和基于特征对象属性的偏好查询，下面分别从这两方面介绍相关工作。

2.1 Top-k 空间关键字查询

传统的Top-k空间关键字查询大多是以用户为查询点，根据兴趣对象与用户之间的空间距离以及与查询关键字之间的文本相关度对兴趣对象进行评分，返回前k个得分最高的兴趣对象给用户[1-5]。比如在欧式空间下，Felipe等人[1]结合R-tree索引和签名文件定义了新的索引结构IR2-tree，研究了距离优先的Top-k空间关键字查询。Qian 等人[2]研究了空间Web 对象与查询关键字之间的语义关系，提出了一种基于语义的Top-k空间关键字查询方法。郭帅等人[3]针对多用户问题研究了协同关键字查询，这种查询考虑了多用户问题，返回距离多个查询位置近、文本与多组查询关键词相关度高的Topk对象。在路网环境下，Rocha-Junior等人[4]研究了基于路网环境的Top-k空间关键字查询，并提出了有效的查询处理方法。陈子军等人[5]提出了基于路网受限的Topk空间关键字查询。给定半径为r的查询范围，基于路网受限的Top-k空间关键字查询，返回靠近查询位置并且与查询关键字文本相关的Top-k个对象。上述工作中提及的Top-k空间关键字查询都是以用户为中心，在查询中仅考虑与用户位置邻近和文本相关的兴趣对象，忽略了兴趣对象周围的其他特征对象属性对于查询结果的重要意义。

2.2 基于特征对象属性的偏好查询

基于特征对象属性的偏好查询，在查询中考虑了兴趣对象周围的特征对象对于用户偏好的满足程度。目前已有不少研究者对此类查询进行了相关研究[6-9]，根据特征对象的属性信息，可将相关研究工作分为两类。

第一类方法考虑了特征对象的空间属性，为每个特征对象预先定义一个分数（由用户评论提供，例如http：//www.zagat.com/，用来评定特征对象的等级）。Yiu等人[6]首次定义了Top-k空间偏好查询并提出了SP算法、GP 算法、BB 算法以及FJ 算法四种查询算法。Top-k空间偏好查询根据满足空间约束关系（范围约束、最近邻约束以及影响区域约束）的特征对象的等级分数来评估兴趣对象。在此之后，Rocha-Junior等人[7]针对上述查询提出了改进方法来解决上述算法查询效率低的问题，该方法定义了一种距离-分数空间，基于此空间提出了一种SFA算法，算法采用Skyline查询，大量地删除与查询结果无关的数据对象，从而有效提高了查询效率。上述所有研究工作都是针对特征对象的空间属性，利用特征对象预定义的分数来处理查询。与上述工作不同，本文研究的Top-k空间关键字偏好查询同时考虑了特征对象的空间属性和文本属性。

随着查询结果质量的不断提高，同时考虑位置邻近性和文本相关性更能够符合用户的实际要求，第二类方法同时关注了特征对象的空间属性和文本属性。Tsatsanifos等人[8]提出了一种Top-k空间-文本偏好查询，查询通过兴趣对象与特征对象之间的距离、特征对象与查询关键字之间的文本相关度以及特征对象的分数来计算兴趣对象的得分。他们提出的查询方法虽然与本文研究工作非常相近，但是本文只考虑了特征对象的空间属性和文本属性。同时，在实际应用中，特征对象并没有一个预定义的分数，因此本文研究的查询更加符合实际应用。De Almeida 等人[9]定义了Top-k空间关键字偏好查询并提出了IFA 算法、SIA 算法和SIA+算法三种查询处理算法，与本文工作相关性较大。然而需要指出的是，他们只处理了基于范围约束和最近邻约束两种查询方式的Top-k空间关键字偏好查询，没有考虑第三种影响区域约束查询方式。本文研究了基于影响区域约束查询方式的Top-k空间关键字偏好查询，提出了有效的剪枝策略以及查询处理方法——GS-NNA算法。

3 基于贪心策略的最近邻算法

3.1 问题描述

兴趣对象集：O={o∈O|o.l=(x,y)},o表示一个兴趣对象（例如，旅馆），o.l代表空间对象位置，(x,y)表示经纬度。

特征对象集：F={f∈F|f.l=(x,y),f.T},f表示一个特征对象（例如，旅馆周围的餐馆、地铁等基础设施），拥有空间属性f.l和文本属性f.T，其中f.l代表特征对象的位置，f.T代表一组关键字集合（例如，餐馆提供的菜单）。

Top-k空间关键字偏好查询：Q={O,F,W,φ,k},O代表兴趣对象集，F代表特征对象集，W={w1,w2,…,w|W|}代表一组查询关键字集合，φ代表影响区域约束，k代表查询结果数量。Top-k空间关键字偏好查询根据兴趣对象周围满足影响区域约束的特征对象来计算兴趣对象的分数，返回得分最高的前k个兴趣对象。

影响区域约束φ要求查找到的目标对象需满足以下条件：（1）距离目标对象最近的特征对象拥有最高的文本相关度；（2）查找到的目标对象拥有的分数高于其他兴趣对象的分数。根据影响区域约束φ，空间区域中每个兴趣对象的得分如式（1）所示：

其中，τφ(o)代表兴趣对象o的得分；θ(f.T,Q.W)代表特征对象f与查询关键字集合W之间的文本相关度，采用余弦公式[10]来计算；dist(f,o)代表兴趣对象o与特征对象f之间的距离，采用欧氏距离计算；r是由用户指定的一个范围，在该函数模型中用来控制兴趣对象得分随距离变化的程度。当给定范围r时，兴趣对象o与特征对象f之间的距离越近，特征对象f与查询关键字集合W之间的文本相关度越高，就表示兴趣对象o的得分越高，更符合用户查询要求。

3.2 算法提出

现有相关研究工作中，只有De Almeida 等人提出的IFA 算法[9]经过改造后可以用来处理本文提出的问题。IFA算法需要检索空间区域中的全部兴趣对象，对于每一个兴趣对象，需要通过文本相关的所有特征对象来计算它的分值，然后选择分值最大的作为兴趣对象的最终得分，最后将空间区域中分数最高的k个兴趣对象返回。然而采用IFA 算法处理Top-k空间关键字偏好查询存在以下三个问题：

（1）IFA 算法需要检索和计算空间区域中所有的兴趣对象；

（2）IFA算法每次只访问一个兴趣对象；

（3）与查询关键字文本相关的所有特征对象都需要参与计算，如果兴趣对象和文本相关的特征对象数量均很大，IFA算法会产生昂贵的计算代价和I/O成本，导致较低的查询效率。

针对上述IFA算法的不足，本文算法重点考虑如何设计有效的剪枝策略，将与查询结果无关的兴趣对象和特征对象进行剪枝。由于Top-k空间关键字偏好查询根据特征对象的属性对兴趣对象评分，特征对象与查询关键字之间的文本相关度越高，则距离该特征对象最近的兴趣对象得分就越高。因此GS-NNA 算法的基本思想是采用一种贪心策略，每次选择与给定查询关键字最相关的特征对象，然后根据该特征对象，从兴趣对象集合中查找距离该特征对象最近的兴趣对象，将它加入到候选结果集中。具体来讲，GS-NNA算法通过倒排文件对特征对象进行文本过滤，然后预先计算倒排文件中所有特征对象与查询关键字之间的文本相关度，并按照相关程度由高到低对它们进行排序。其次，设置阈值判定条件，用来剪枝与查询结果无益的兴趣对象和特征对象。最后，利用最近邻方法查找与文本相关度最高的特征对象距离最近的兴趣对象。通过上述方式查找到的兴趣对象将拥有最高的分数。

因为Top-k空间关键字偏好查询需要处理两种数据对象：兴趣对象和特征对象，所以针对两种数据对象的属性特征，本文算法采用不同索引结构来索引它们。算法采用R*-tree[11-12]索引兴趣对象，将距离彼此接近的兴趣对象存储到同一个节点中。采用倒排文件[13-15]索引特征对象，过滤掉与查询关键字不相关的特征对象。倒排文件中每个倒排列表对应一个查询关键字w，列表中存储包含w的特征对象的id以及w在该特征对象文本中出现的频率ft。同时，为了便于计算特征对象与兴趣对象之间的距离，在倒排列表中存储了特征对象的位置信息f.l。

图1给出了GS-NNA算法查询处理流程图，算法具体执行过程如下：

（1）访问倒排文件。按照id顺序访问和计算每个特征对象f与查询关键字W之间的文本相关度，并按照相关程度将特征对象f存储在堆U中。U中每个节点存储特征对象f的id、位置信息f.l以及与查询关键字之间的文本相关度θ(fi.T,Q.W）。

（2）访问堆U。每次从U中取出与查询关键字相关度最高的特征对象fθmax，根据式（1）计算Tφ(fθmax)。其中取距离值为 0，Tφ(fθmax)=θ(fθmax.T,Q.W) 。比较Tφ(fθmax)与阈值τ：如果Tφ(fθmax)＞τ，执行步骤 3；否则结束查询，执行步骤5。

（3）访问R*-tree。如果是首次访问R*-tree，则查找特征对象fθmax的k个最近邻兴趣对象oj(j=1,2,…,k),计算它们的得分τφ(oj)。然后比较τφ(oj)和阈值τ,如果τφ(oj)＞τ，将oj按照分值降序存储到结果集H中，更新H和τ；否则执行步骤2。

（4）如果不是首次访问R*-tree，则查找fθmax的最近邻兴趣对象oNN，计算τφ(oNN)。比较τφ(oNN)与阈值τ：如果τφ(oNN)＞τ，将oNN按照分值降序添加到H中，更新结果集H和阈值τ，然后继续查找fθmax的下一个最近邻oNN，直到τφ(oNN)≤τ时，结束当前查询，返回步骤（2）。

（5）返回查询结果集H。

图1 GS-NNA算法处理流程图

这里对更新查询结果集H和阈值τ进行简要说明。如果 |H|＜k且τφ(oj)＞τ，则将兴趣对象oj按照分数降序添加到H中；如果 |H|≥k且τφ(oj)＞τ，则删除H中第k个对象，将oj按照分数降序添加到H中，并用当前H中第k个对象的得分更新阈值τ。

由上述查询流程得出GS-NNA算法：

为了更清楚地解释GS-NNA算法的查询过程，本文将结合实例对算法进行说明。图2 所示的是一个空间区域S，其中黑点表示兴趣对象（旅馆）oj∈O(j=1,2,…,8)，白点表示特征对象fi∈F(i=1,2,…,6)，用二维坐标(x,y)表示它们的地理位置信息。表1记录了每个特征对象fi的详细信息，包括名称Name以及关键字信息f.T。

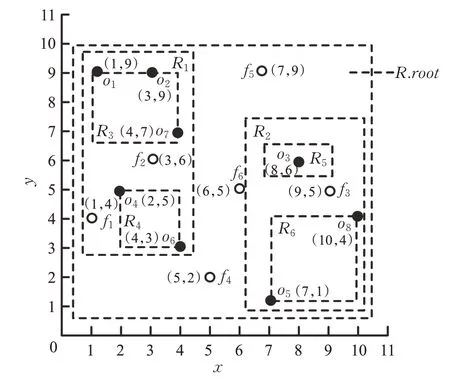
图2 一个空间区域S

表1 特征对象集文本属性

假设一名游客想要查找一家旅馆，要求附近存在提供“Coffee”和“WiFi”的餐馆。这是一个Top-k空间关键字偏好查询，其中“Coffee”和“WiFi”为查询关键字。图3是根据图2 中的数据所创建的索引结构，图3（a）是R*-tree 索引，图3（b）是为查询关键字“Coffee”和“WiFi”创建的倒排列表。

图3 索引结构

本文分别采用GS-NNA 算法和IFA 算法执行该示例中的Top-k空间关键字偏好查询。

首先采用GS-NNA 算法进行查询，指定r=1.7，具体查询步骤如下：

（1）访问倒排列表，则U={f3,f1,f4,f6}。

（2）初始阈值τ=0 ，访问U，从U中取出fθmax，即f3,Tφ(fθmax)=Tφ(f3)=θ(f3.T,Q.W)=2＞τ（为了便于计算，实例中采用关键字出现的次数作为文本相关度，而在实验部分采用余弦公式计算）。

（3）如果执行Top-1查询，则f3的最近邻oNN为o3，返回步骤（2），继续访问U，从U中取出下一个fθmax，即f1,Tφ(f1)=θ(f1.T,Q.W)=1＜τ=1.124 ，因此查询结束，返回结果集H。

（4）H={o3}。

（5）如果执行Top-2 查询，f3的最近邻为o3和o8，重复执行步骤2，结束查询，理由同上，返回结果集H。

（6）H={o3,o8}。

采用IFA 算法执行Top-k空间关键字偏好查询。算法需要检查空间区域S中所有的兴趣对象，对于每一个兴趣对象oi(i=1,2,…,8)，需要访问倒排文件，取出所有的特征对象存储到U中，U={f1,f3,f4,f6}。然后按照id顺序计算每个特征对象的文本相关度，以及它们与oi之间的距离，最后根据式（1），计算每个兴趣对象oi的分数3,4,6。经过计算，每个兴趣对象oi的分数分别为：

经过比较τφ(oi)和τ，查询返回o3作为Top-1结果，o8作为Top-2结果。

结合上述实例发现，采用IFA 算法执行查询时，需要检索和计算空间区域中每一个兴趣对象的得分，从而导致较高的计算代价和I/O 成本，使得查询效率较低。相比之下，采用GS-NNA 算法执行查询时，因为每次只查找文本相关度最高的特征对象的最近邻作为候选结果，大量与查询结果无关的兴趣对象和特征对象被剪枝，所以有效减少了计算成本，提高了查询效率。通过上述实例可以明显看出GS-NNA算法更具优势。

3.3 算法复杂度分析

本节主要对GS-NNA 算法和IFA 算法的复杂度进行简要分析，两种算法的复杂度主要从需要检索的特征对象数量和兴趣对象数量两方面进行考虑。假设兴趣对象集中兴趣对象的数量为 |O|，特征对象集中特征对象的数量为 |F|。对于IFA 算法，由于采用倒排文件过滤了与查询关键字不相关的特征对象，并计算了空间数据集中所有的兴趣对象，因此IFA 算法的复杂度为O(|O|× |F′|)，其中F′⊆F。对于GS-NNA算法，由于算法每次从倒排列表中选取文本相关度最高的特征对象，通过该特征对象查找距离它最近的兴趣对象，并利用阈值判定条件，将不满足阈值条件的特征对象和兴趣对象进行剪枝，有效减少了需要访问和计算的特征对象和兴趣对象的数量，因此GS-NNA 算法的复杂度为O(|O′|×|F′|)，其中O′⊆O，F"⊆F′⊆F。

4 实验结果与分析

4.1 实验设置

实验在三个真实数据集Venice、London 和North America 上进行，数据集的相关属性如表2 所示。本文所有算法均采用Java 语言实现，实验在Windows 10 系统上进行，系统配置为8 GHz 内存的Intel®CoreTMi3-6100 CPU@3.70 GHz处理器。

4.2 实验结果

实验从查询关键字的数量、查询结果数量k以及数据集基数三方面来衡量IFA 算法和GS-NNA 算法对查询响应时间的影响。实验参数具体设置如表3所示。

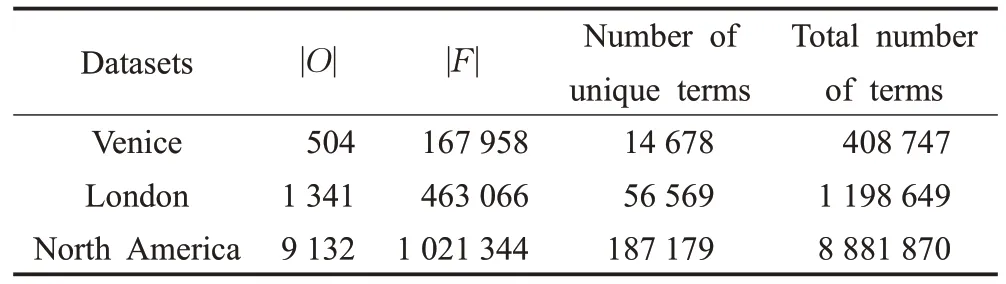
表2 实验数据集属性

表3 实验参数设置

4.2.1 查询关键字数量变化对查询响应时间的影响

图4 展示了当固定查询结果数量为5、数据集为Venice 时，不同查询关键字数量对查询响应时间的影响。从图4中可以看出，GS-NNA算法查询响应时间比IFA算法要快，并且随着查询关键字数量的增加，IFA算法和GS-NNA算法都有所增加，但是GS-NNA算法增加幅度微小。由于IFA 算法仅能通过倒排文件对特征对象进行文本过滤，当查询关键字数量增加时，文本相关的特征对象数量将会增加，导致剪枝效果较差，从而导致查询时间增加。而GS-NNA 算法采用倒排文件和阈值判定条件对特征对象进行剪枝，只有同时满足文本相关和阈值判定条件的特征对象才能参与计算，因此GS-NNA算法查询响应时间增加的程度要小于IFA算法。

图4 查询关键字数量对查询响应时间的影响

4.2.2 参数k 变化对查询响应时间的影响

图5 展示了当固定查询关键字数量为3、数据集为Venice时，查询结果数量k变化对于查询响应时间的影响。从图5 中可以看出，当k增加时，两种算法的查询响应时间受到的影响非常小，而GS-NNA算法仍然保持优势。这是因为IFA 算法已经访问和计算了所有的兴趣对象，当k值增加时，只需要从候选结果集中返回前k个兴趣对象即可，所以并不会影响查询响应时间。而对于GS-NNA算法，因为查询结果从文本相关度最高的特征对象的最近邻中选择，所以当k值增加时，需要搜索特征对象最近邻的时间增加，从而导致整体查询时间增加。但是由于GS-NNA算法采用了有效的剪枝策略，相对于整体查询时间，搜索最近邻的时间具有微小的影响。

图5 参数k 对查询响应时间的影响

4.2.3 不同大小的数据集对查询响应时间的影响

图6 展示了当固定查询关键字数量为3、查询结果数量k为5时，不同大小的数据集对于查询响应时间的影响。从图6 中可以看出，随着数据集基数的增大，两种算法的查询响应时间也随之增加。主要原因是当数据集基数增加时，表示兴趣对象和特征对象的数量均增加。其中特征对象数量的增加并不会影响到查询效果，因为参与查询的特征对象数量只与查询关键字数量的变化相关。而兴趣对象数量的增加将会影响两种算法的查询响应时间，尤其是IFA算法受到的影响更大。这是因为IFA 算法需要访问和计算所有的兴趣对象，而GS-NNA 算法仅搜索和计算满足阈值判定条件的特征对象的最近邻，所以查询响应时间上要快于IFA算法。

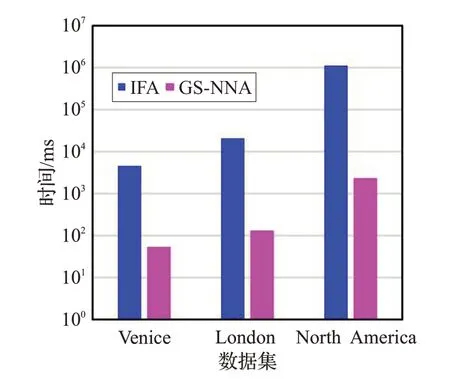
图6 不同大小的数据集对查询响应时间的影响

5 总结

本文提出了一种基于贪心策略的最近邻查询算法GS-NNA，该算法结合R*-tree 索引和倒排文件索引，有效解决了基于影响区域偏好约束的Top-k空间关键字偏好查询方式下，访问和计算代价大的问题。具体地，算法利用贪心思想，每次选择与用户查询需求最匹配的特征对象，然后通过最近邻方法遍历R*-tree，查找距离该特征对象最近的兴趣对象，将此兴趣对象作为候选结果返回。GS-NNA算法为了更进一步提高查询效率，设置了阈值判定条件，将不满足阈值判定条件的特征对象和兴趣对象进行剪枝，减少了需要访问和计算的数据量。最后，通过与IFA算法进行实验比较，证明了GS-NNA算法比IFA算法在查询响应时间上快了一个数量级，有效提高了查询效率。