公路桥梁墩柱竖直度检测与评价

甯家成，谢应爽

(重庆市公路工程质量检测中心，重庆 400060)

0 前 言

随着交通强国战略的推进，高等级公路建设不断加密，大跨径高墩桥梁越来越多。对高墩桥梁而言，桥梁墩柱竖直度关系重大，严重影响桥梁结构受力，影响桥梁结构安全和使用寿命。

桥梁墩柱竖直度检测主要用于施工过程控制和交工验收对墩柱初始状态检测评价。桥梁墩柱竖直度检测方法主要有垂线法和全站仪测量法。研究发现，常规的竖直度检测只针对墩柱底和墩柱顶两个断面的特征计算水平偏移和倾斜率，不能检测出墩柱中心轴线的空间线形。同时桥梁墩柱施工的初始倾斜、承台或基桩下沉、外部荷载作用和表面凹凸现象引起倾斜或倾斜假象，不能有效区分和排除[1]。因此，亟需在原有方法的基础上进行改进。

本文结合实践经验对垂线法、全站仪检测圆柱墩和矩形墩的竖直度进行了总结分析和改进，并采用最小二乘法计算竖直度参数，提高了结果的精度和可靠性。

1 垂线法

垂线法较常见的是在墩柱顶部位置上，直接或支出一点悬挂适当重量的垂球，在垂线上下部读取(采用网格读书板时)或量出观测点的水平位移。计算上下两点位移差，并记录位移方向。

垂线法除悬挂垂球外，也可用激光垂准仪发射激光束做参考垂线。检测时激光垂准仪务必严格整平、对中，保证激光束铅垂。

公路工程质量检验评定标准要求检查纵、横两个方向竖直度。故采用垂线法检测时分别在纵桥向和横桥向两个不同方向吊垂球或架设激光垂准仪，测量墩柱顶相对墩柱底的位移偏移量。垂线法检测竖直度示意如图1，具体步骤如下。

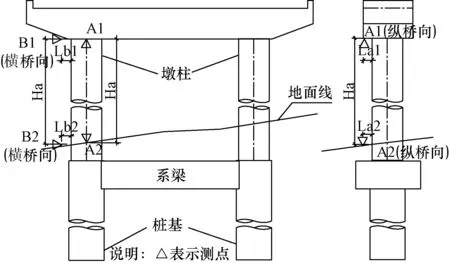
图1 垂线法检测竖直度示意图

1.1 数据采集

测量纵桥向偏移值时，分别测量上吊点(或垂准仪激光光斑)与纵桥向测点A1的距离La1，下吊点(或垂准仪架设中心)与纵桥向测点A2的距离La2。同时测量测点A1和测点A2的距离Ha。

测量横桥向偏移值时，分别测量上吊点(或垂准仪激光光斑)与横桥向测点B1的距离Lb1，下吊点(或垂准仪架设中心)与横桥向测点B1的距离Lb2。同时测量测点B1和测点B2的距离Hb。

1.2 数据计算分析

纵桥向偏移值：δ1=La1-La2，检测高度Ha，方向根据δ1正负判断；横桥向偏移值：δ2=Lb1-Lb2，检测高度Hb，方向根据δ2正负判断。

垂线法原理简单，但一般只能反映顶部底部特征点倾斜情况，对成桥状态的墩柱竖直度检测时常需要桥检车配合，若采用垂球吊垂线，对于高墩柱或多风地区，垂球会摆动干扰较大。采用激光垂准仪检测虽精确度高，但部分桥梁墩柱施工完成后底部已不具备架设仪器的条件。故垂线法常用于施工过程检测，或高度较低的墩柱竖直度检测。

2 全站仪法

随着测量技术的发展和精度的提高，全站仪自动化程度越来越高，搭载的面向用户使用程序越来越多。其中包括自由设站功能和免棱镜无接触测点功能，这使得采用全站仪测量桥梁墩柱竖直度更为方便快捷和准确可靠。公路桥梁中墩柱截面的形式多为圆形或矩形。下面分别介绍采用全站仪测量圆形墩柱和矩形墩柱的竖直度方法。

2.1 圆形墩柱的竖直度检测

对圆形墩柱首先利用全站仪的自由设站功能，通过参考点建立纵桥向、横桥向的坐标系，再快速采集墩柱上中下多个断面的圆柱体坐标，每个断面各采集3个以上的点坐标(常取4个点，位置分开不重合)，再计算出各断面圆心坐标和总高差[2]。通过对圆心坐标拟合得墩柱变形曲线，进而计算出墩柱的倾斜量和倾斜方位。圆形墩柱竖直度检测示意如图2，具体步骤如下。

图2 圆形墩柱竖直度检测示意图

2.1.1 数据采集

1)建立检测坐标系：选择合适位置架设仪器(一次尽可能检测多个墩柱)，通过参考点给全站仪建立横桥向和纵桥向的测站。可以路线前进方向(纵桥向)为X轴正方向，面向路线前进方向横桥向左侧为Y轴正方向，铅垂向上为Z轴正方向。

2)特征断面点坐标测量：根据墩柱高度，除靠顶部和底部的断面外，在墩身大致均匀布置若干(一般2个)能反应墩柱特征的柱坐标采集断面。在测站建好后，采用无棱镜点坐标测量模式，测量各采集断面4个不同点Ai、Bi、Ci、Di的坐标(xi1，yi1，zi1)，(xi2，yi2，zi2)，(xi3，yi3，zi3)，(xi4，yi4，zi4)。

2.1.2 数据计算分析

1)计算圆心坐标：根据各特征断面点Ai、Bi、Ci、Di坐标计算圆心Oi坐标(Xi，Yi，Zi)。由于误差，Ai、Bi、Ci、Di四个点，并不完全在同一个圆周上，且高程坐标也存在细微差异。计算时4个点视为在同一高度，Zi取4个点高程的平均值。根据3个点可以确定一个圆，故通过4个点中每3个点的x,y坐标均计算得一个圆心坐标，最后取平均值作为该断面圆心Oi的坐标。

2)根据圆心坐标拟合墩柱变形曲线：求出圆心坐标后，根据X1、X2、……、Xn和对应高程坐标，按墩柱变形规律采用最小二乘法拟合出墩柱纵桥向的变形曲线。墩柱变形曲线近似为二次抛物线，故可采用抛物线基本方程X=A1Z2+B1Z+C1按最小二乘法拟合。其中系数A1、B1、C1为如下三元一次方程组的解。

同理，根据Y1、Y2、……、Yn和对应高程坐标，按最小二乘法拟合得横桥向变形曲线方程Y=A2Z2+B2Z+C2。

3)计算墩柱偏移值：纵桥向偏移值δ1=X(Z1)-X(Zn)；横桥向偏移值δ2=Y(Z1)-Y(Zn)；根据取值的正负判断偏位的方向。

2.2 矩形墩柱的竖直度检测

矩形墩柱由于自身存在相互垂直面，故用本身点便可方便建立纵、横桥方向坐标系，无需像圆形墩柱采用其他参考点建立观测坐标系。矩形墩柱竖直度检测示意如图3，具体步骤如下。

图3 矩形墩柱竖直度检测示意图

2.2.1 数据采集

1)参考点坐标测量：找一个能同时观测纵、横桥向面的位置(也可分别两个方向检测，本文不做讨论)，架设全站仪。在纵桥向面底部利用水平尺标记参考点E1和E2(E1和E2在同一水平面上，任意间距均可)。在同一高度的横桥向面同样标记参考点F1和F2。测量E1坐标(x11,y11,z11)、E2坐标(x21,y21,z21)、F1坐标(x12,y12,z12)、F2坐标(x22,y22,z22)。

2)特征点坐标测量：根据墩柱高度在墩身大致均匀位置，检测若干个能反应墩柱特征的点(底部利用控制点，每面顶部1个测点，中间若干点，各点尽量靠近轴线)，并采用无棱镜坐标测量模式测量纵桥向面上各点Ei的坐标(xi1,yi1,zi1)和横桥向面上各点Fi的坐标(xi2,yi2,zi2)。

2.2.2 数据计算分析

横桥向竖直度计算方法和纵桥向一致，故计算过程以纵桥的竖直度计算为例。

2)计算E1E2铅垂面方程：E1E2铅垂面方程为A(X-x11)+B(Y-y11)+C(Z-z11)=0，化简为：A(X-x11)+B(Y-y11)=0。其中E1的坐标(x11,y11,z11)也可以用E2的坐标(x21,y21,z21)代替参与计算。

3)计算纵桥向面上各点Ei(xi1,yi1,zi1)到E1E2铅垂面距离di1：

由此计算得E2、E3、……、En各点到E1E2铅锤面的距离d21(为0)，d31、……、dn1。

5)计算纵桥向墩柱偏移值：δ1=D1(zn1)-D1(z21)，偏位方向根据计算值的正负判断。

3 工程实例

以某高速公路一匝道立交桥圆柱墩的竖直度检测为例。墩柱编号为1-0#，直径1.8 m，高30.8 m。该墩柱临近悬崖边，故采用全站仪进行检测。检测时以纵桥方向大桩号为X轴正方向，面向大桩号横桥向左侧为Y轴正方向，竖直向上为Z轴正方向建立坐标系。约10 m布置一个检测断面，共4个检测断面，各特征断面点坐标检测数据见表1,表中数据已精确至mm。

表1 各特征断面点坐标检测数据

根据各断面检测点Ai、Bi、Ci、Di坐标计算圆心坐标(Xi，Yi，Zi)得：O1(31.063,4.055,29.106)，O2(31.065,4.054,19.148)，O3(31.056,4.056,8.299)，O4(31.062,4.056,-1.018)。

分别对纵、横桥方向数据采用最小二乘抛物线拟合。拟合出纵桥向变形曲线方程为：X=9.243×10-6Z2-1.342×10-4Z+31.0604(单位:m)；横桥向变形曲线方程为：Y=2.744×10-6Z2-1.274×10-4Z+4.0561(单位:m)。

故纵桥向偏差为δ1=X(Z1)-X(Z4)=3.8mm，方向为大桩号侧；横桥向偏差为：δ2=Y(Z1)-Y(Z4)=-1.5mm，方向为横桥向右侧。

对于公路桥梁墩柱竖直度检测结果均按《公路工程质量检验评定标准.第一册.土建工程》(JTG F80/1—20017)中相关的要求评定。以该标准JTG F80/1—20017为例：高度H≤5 m，允许偏差≤5 mm；5 m60 m，允许偏差≤H/3000,且≤30 mm。[3]故1-0#墩柱的允许偏差为20 mm，其纵桥向和横桥向竖直度均合格。

[ID:010014]