基于SSA-PPR模型的河流枯季径流量变化预测方法

胡 鑫

(云南省水文水资源局曲靖分局,云南 曲靖 655000)

0 引 言

预测河流径流量变化情况有利于水利建设工程的设计，降低水利施工过程中事故发生的概率[1-3]。相关河流枯季径流量变化预测方法研究在水利建设和农业灌溉等领域中具有广泛的应用价值[4-6]。

现有方法中，有研究人员将大样本数据模型方法应用在中小河流流量测验中。该方法根据表面流速、断面水位数据，构建河道断面水位-流量关系曲线。运用该曲线分析河道水位-流量的关系特性，根据二者之间的关联性实现对河流流量的预测。实验结果表明：该方法可以减少流量测量的工作量，但是预测精度不高[7]。另有学者利用低空遥感无人机影像反演河道流量，实现对河流流量变化的预测。该方法运用无人机影像采集水面宽、糙率、水面比降信息，结合上述信息通过水力学方法计算河道流量，将计算结果作为参考实现对河流流量的预测。结果表明，该方法得到的预测结果略高于实测结果，并且存在预测效率不高的问题，未来仍需进一步提高预测结果的精度，降低预测用时[8]。除上述方法外，还有学者提出了基于CORDEX数据集的碧流河流域径流预估方法。该方法利用气象数据集构建SWAT水文模型，用于预测气候变化条件下碧流河流域的径流过程，得到径流量的变化特征，通过计算得出具体的径流量预测值[9]。

针对上述问题，为提高河流枯季径流量的定量预测能力，本文提出一种基于SSA-PPR模型的河流枯季径流量变化预测方法。

1 河流枯季径流量变化大数据统计分析

1.1 构建流量变化大数据统计分析模型

为了实现对河流枯季径流量变化的预测，采用SSA-PPR(Singular Spectrum Analysis-Projection Pursuit Regression，奇异谱分析-投影寻踪回归)模型构建河流枯季径流量变化预测的大数据统计分析模型，并采用描述性统计分析方法，进行河流枯季径流量的关联特征分析，提取变化预测特征量。结合模糊信息相关性预测方法，进行河流枯季径流量变化的流量序列建模，得到流量时间分布序列为：

A(x)=AJ(x)a(x)+D(1-b(x))

(1)

其中，A={a1,a2,…,an}为河流枯季径流量变化的动态分布特征集，D={d1,d2,…,dm}为河流枯季径流量的负载强度分布集。在河流枯季径流量变化预测过程中，采用有向图分析模型G=(V,E,W)表示河流枯季径流量变化的统计分布，其中，V为河流枯季径流量变化的自相关分布集，V={v1,v2,…,vN}。根据河流枯季径流量变化的波动性和负载均衡性，进行负载均衡控制，河流枯季径流量变化的特征分布集为(u,v)∈E，表示河流枯季径流量变化的统计特征量之间的自相关系数，W={ω1,ω2,…,ωm}为径流量变化的动态权重。采用高维相空间重构技术，进行河流枯季径流量变化序列的空间重组，得到重构的相空间为：

=[x(t0),x(t1+Δt),…,x(tm+(K-1)Δt)]A(x)

(2)

其中，x(t)为径流量变化的动态特征分布集，J是扰动窗口函数，m是河流枯季径流量变化的嵌入维数，Δt表示径流量变化的跳变时间宽度。根据空间重构结果可以得出径流量变化状态特征分布的概率密度为：

wij=Xβ×w(epkq)，β>1

(3)

其中，β为正定周期解，w(epkq)表示径流量变化的波动系数，根据公式(3)得到河流枯季径流量变化的差异性判别函数为：

(4)

其中，α为河流枯季径流量变化的自适应调节系数，其取值范围为0≤α≤1，Ts为河流径流量年内分配不均匀系数。根据上述分析，建立河流枯季径流量变化的时间序列分布模型，根据时间序列采样结果进行流量变化动态分析和变化特征重组。

1.2 河流枯季径流量变化的大数据量化特征分析

受天气等因素的影响，河流枯季径流量具有实时变化性，夏季气温和降水量的突然变化会引起河流径流量突然增大，因此，采用量化统计特征分析方法对受外在因素影响的河流径流量变化特征进行动态分析，并对变化特征重组结果进行特征挖掘，得出河流枯季径流量变化统计特征量。根据河流枯季径流量变化特征分析结果，获取河流枯季径流量变化的二乘规划统计特征分布集：

(5)

(6)

其中，G={G1,G2,…,Gn}为河流枯季径流量变化的主成分特征量。采用模板匹配方法，获取河流枯季径流量变化的自适应加权系数[15-18]，得到加权矩阵为：

(7)

采用自适应学习方法结合自适应加权系数，得到河流枯季径流量变化的拟合系数为S={B(x1,y1,u(x1)),…,B(xj,yj,u(xj))}，其中xj∈Rn，u(xj)∈{-1,1}，σ≤u(xj)≤1，σ为河流枯季径流量变化统计的模型参数，u(xj)为河流枯季径流量变化(xj,yj,u(xj))的输出。根据上述分析，实现对河流径流量变化特征的动态分析，并对径流量动态变化特征进行挖掘：

(8)

其中，c(i)为河流流域地形指数特征值，n为河流枯季径流的统计特征，N为河流估委径流的混沌特征。

在挖掘过程中将无效特征数据进行剔除，得到变化统计特征量，并结合模糊信息挖掘和自适应学习方法得到了河流枯季径流量变化的动态解析结果。

2 基于SSA-PPR模型的河流枯季径流量变化预测

2.1 河流枯季径流量预测的SSA-PPR模型构建

根据上述得出的变化统计特征量和河流枯季径流量变化的动态解析结果，基于SSA-PPR模型构建河流枯季径流量变化预测模型，SSA-PPR模型函数为：

(9)

其中，ξj为河流枯季末滞留于流域内的蓄水量，ξj≥0，j=1,2,…,l。以河流枯季径流量变化的主成分特征为参考特征量，引入高维相空间重构，得到河流枯季径流量变化的模型分布核函数K(xi,xj)，则河流枯季径流量变化的线性规划函数为：

(10)

其中，αi为气候因素影响下流域内的径流量，αj为气候因素影响下流域内的径流损失量，0≤αj≤1，j=1,2,…,l。对河流枯季径流量的变化进行线性规划设计，得到河流枯季径流量变化预测的优化传递函数为：

(11)

其中，h(t)为河流枯季径流量变化预测的优化传递函数，M为枯季径流过程中的变异点总量，K(m)为变异点的显著性指数，αmk为枯季径流过程中的变异点特征，δ为流域内地表径流量，t为该区径流量年际变化系数，Tm为径流量的年际变化指数，τmk为降水量的年际变化指数。根据优化传递函数分析河流枯季径流量变化的统计结果：

(12)

其中，∂ui为枯季径流上游降水补给量，Gh(t)为河流枯季径流量总体变化特征参数，∂pi为枯季径流下游降水补给量，hj为枯季平均降水量，pj为枯季平均降水量占年降水量的比重，γi为平均气温，β为枯季流量占总径流量的比重。根据统计分析结果，进行河流枯季径流量变化特征分解，得到多维尺度特征分布为：

(13)

其中，pdrop为河流枯季径流量变化的SSA-PPR模型参数，Ecomm为径流消耗含水层内积聚的水量，任意选取一采样周期进行SSA-PPR模型调度，构建SSA-PPR模型的输出特征集为CHi(i∈C1)，实现河流枯季径流量变化的优化预测，结果输出为：

(14)

(15)

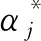
2.2 河流枯季径流量变化预测结果输出

根据河流枯季径流量变化的特征进行流量变化的动态分类识别[19-23]，河流枯季径流量变化的多维结构分解的时间尺度为：

Yk=[yk1,yk2,…,ykj]b*

(16)

其中，ykj表示河流枯季径流量变化的不平衡特征量，k=1,2,…,N，N为河流枯季径流量变化数据长度，依据河流枯季径流量变化的结构特征，得到河流枯季径流量变化的预测分量为：

z(t)=Yk+x(t)+iy(t)-a(t)eiθ(t)

(17)

其中，x(t)表示河流枯季径流量变化的自相关特征分量，y(t)表示河流枯季径流量变化的模糊特征集，a(t)为地表形态特征，eiθ(t)为流域的高程特征值。结合SSA-PPR模型，实现对河流枯季径流量变化特征的融合，得到融合结果为：

maxF(X)=z(t)·(F1(X),F2(X),…,Fn(X))

(18)

最终得到河流枯季径流量变化预测的迭代式为：

(19)

综上分析，结合模糊信息挖掘和自适应学习进行河流枯季径流量变化的动态解析和预测，根据河流枯季径流量变化的特征融合结果进行流量变化的动态分类识别，依据优化统计分析和动态分类识别结果实现对河流枯季径流量变化的准确预测。

3 仿真实验与结果分析

通过仿真实验验证本文方法在实现河流枯季径流量变化预测中的应用性能，以某流域近40年(1980-2019)冬季河流径流量为实验数据，具体数据见表1，并通过在线数据分析软件MOA(一种用于大型数据在线分析的实验工具)进行数据分析，得出河流枯季径流量采样的时域分布如图1所示。

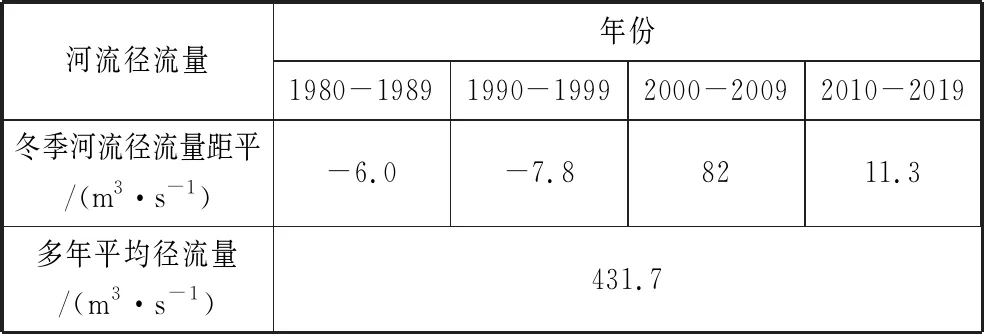
表1 某流域近40年冬季河流径流量

图1 河流枯季径流量采样时域分布

根据图1中的河流枯季径流量采样结果，采用本文方法进行河流枯季径流量的变化预测，结果如图2所示。

(a) 训练样本

(b) 测试样本

分析图2得知，本文方法能有效实现对河流枯季径流量变化预测，其中测试样本与训练样本的拟合性较好，说明本文方法的预测收敛性较好。

为验证本文方法在预测精度方面的优势，将本文方法与基于大样本数据模型的中小河流流量预测方法(文献[7]方法)、基于低空遥感无人机影像反演的河道流量预测方法(文献[8]方法)和基于CORDEX数据集的碧流河流域径流预估方法(文献[9]方法)进行对比，得出对比结果见表2。

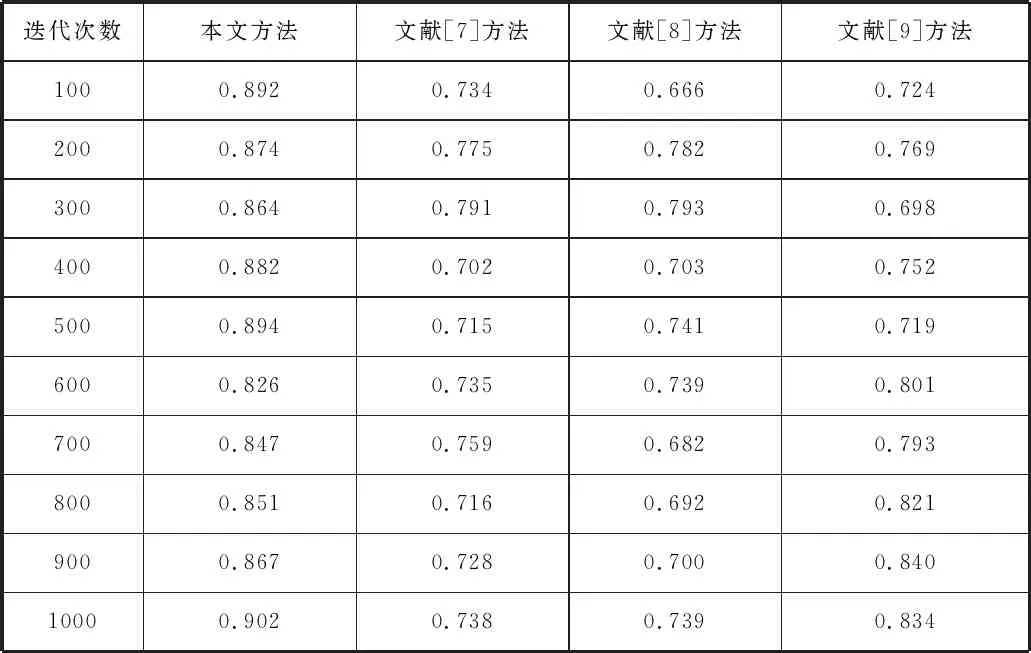
表2 不同方法预测精度对比

分析表2得知，采用本文方法对河流枯季径流量变化进行预测时，预测精度最高值达到了0.902，最低值为0.826；采用文献[7]方法对河流枯季径流量变化进行预测时，预测精度最高值达到了0.791，最低值为0.702；采用文献[8]方法对河流枯季径流量变化进行预测时，预测精度最高值达到了0.793，最低值为0.666；采用文献[9]方法对河流枯季径流量变化进行预测时，预测精度最高值达到了0.840，最低值为0.719。根据上述数据可知，本文方法的预测精度高于文献[7]方法、文献[8]方法和文献[9]方法，说明本文方法在流量变化预测方面具有明显的优势。这是由于本文方法在大数据统计分析模型的基础上，采用特征分析方法对径流量动态变化特征进行挖掘，挖掘过程中可有效剔除无效特征数据，降低了河流枯季径流量的实时变化给预测精度带来的影响。

为了进一步验证本文方法的应用性能，以预测效率为指标，将本文方法与文献[7]方法、文献[8]方法和文献[9]方法进行对比，结果如图3所示。

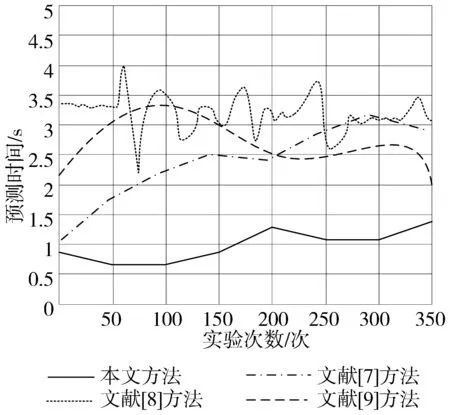
图3 不同方法的预测时间对比

分析图3可知，运用本文方法对河流枯季径流量变化进行预测时，预测用时始终低于1.5 s，而文献[7]方法的预测用时保持在1.5 s～3.5 s之间，文献[8]方法的预测用时保持在2.0 s～4.0 s之间，文献[9]方法的预测用时保持在2.0 s～3.4 s之间。根据上述数据可知，本文方法的预测效率更高，可以更快地为水利工程提供相关数据，辅助水利工程的实施。

上述仿真测试结果表明，本文实现了对河流枯季径流量的动态监控，并通过对比，展示了本文方法在提高河流枯季径流量变化预测能力方面的优越性能。

4 结束语

本文对河流枯季径流量进行预测研究，提出一种基于SSA-PPR模型的河流枯季径流量变化预测方法。首先提取河流枯季径流量的变化预测特征量，结合模糊信息相关性预测方法，进行河流枯季径流量变化的流量序列建模，然后采用模板匹配方法，获取河流枯季径流量变化的自适应加权系数，采用SSA-PPR模型构建河流枯季径流量变化预测的大数据统计分析模型，针对优化统计分析结果进行河流枯季径流量变化的准确预测。分析得知，采用本文方法进行河流枯季径流量变化预测的准确性较高，自适应性较好，解决了河流枯季径流量实时变化对预测精度的影响，对量化分析河流枯季径流量变化具有很好的指导意义。