多目标产品配置优化研究

詹钧凯，石宇强，陈柏志，蔡跃坤

（西南科技大学制造科学与工程学院，四川 绵阳 621010）

1 引言

随着全球化市场竞争的加剧和顾客需求的多样化，卖方市场转变为买方市场，快速响应并提供满足顾客个性化需求的高性能、低成本、短交货期的产品配置方案逐渐成为企业的战略选择，产品配置是实施大规模定制的核心环节，其实现依赖于灵活的配置模型和高效的求解方法[1]。

配置模型方面：文献[2]在模块和目标约束下以性能、成本、交货期为目标建立配置模型。文献[3]考虑互斥和依耐性约束以响应时间、成本和质量为目标构建配置模型。上述研究缺乏对顾客个性化需求约束的考虑；配置模型求解方面：文献[4]采用改进的线性加权和算法求解多目标配置模型。文献[5]采用线性加权方法将多目标转化为单目标，并应用遗传算法求解配置模型。文献[6]采用改进的蚁群算法进行配置求解。文献[7]应用NSGA-Ⅱ算法对成本、响应时间和综合服务性能进行配置优化。上述研究存在算法有效性不佳的问题。

针对以上研究存在的不足，在考虑顾客个性化需求等约束，建立以性能、成本和交货期为目标的产品配置模型，设计了一种改进的NSGA-Ⅱ算法求解配置模型，并根据顾客偏好推荐配置方案。

2 多目标产品配置模型

2.1 问题描述

针对模块化产品族S，产品配置过程为：根据顾客需求从必选配置模块的每个配置单元中选取1 个零部件，从可选配置模块的每个配置单元中至多选取1 个零部件，最终构成一个产品性能最大化，成本和交货期最小化，且满足一定约束的产品。

设Ohlk为第h 配置模块（h=1 为必选配置模块，h=2 为可选配置模块）的第l（l=1，2，L，Mh）个配置单元的第k（k=1，2，L，Dhl）个零部件实例。决策变量xhlk如下：

2.2 目标函数

最大化产品性能：

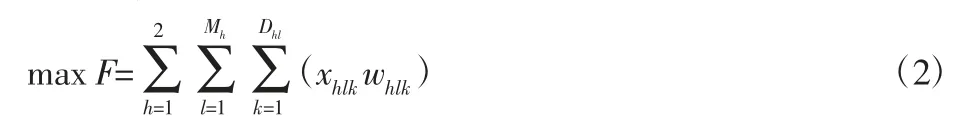
式中：whlk—零部件实例Ohlk与客户需求的性能相关度。

最小化产品成本[8]：

式中：Chlk—零部件实例Ohlk的采购成本；Ca—零部件间的平均装配成本系数；CF—固定成本。

最小化交货期：

式中：Thlk—零部件实例Ohlk的制造工期；Ta—零部件间的平均装配工时系数；Tr—物流运输时间。

2.3 约束条件

式中：a—企业利润率；Cmax—成本上限。

式中：Tmax—交货期时间上限。

基本约束，即从必选配置模块的每个配置单元中只选取1个零部件，从可选配置模块的每个配置单元中至多选取1 个零部件。

关系约束，包含相容和互斥2 种情况，相容的零部件在产品中必须同时存在，互斥则不能同时存在。

个性化约束，即顾客指定产品中必须有或不能有的零部件。

3 改进的NSGA-Ⅱ算法设计

3.1 编码设计

采用十进制编码法。每一个体表示一个产品配置方案，个体编码如下：Code=V11kV12kLV1M1kV21kV22kLV2M2k

基因Vhlk表示第h（h=1 为必选配置模块，h=2 为可选配置模块）配置模块的第l（l=1，2，L，Mh）个配置单元的第k 个零部件实例。每个基因Vhlk表示一个配置单元，基因占位长度由该配置单元所含零部件数决定，基因值为k，当配置单元没有零部件被选中时，用0 占位。

3.2 适应度函数

将最大化产品性能指标F 乘以-1 转化为求最小值指标，产品性能、成本和交货期适应度函数如下：

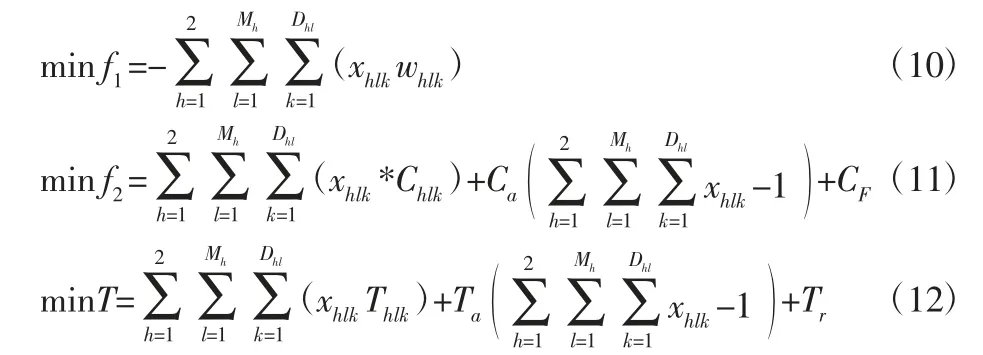
对违反约束的配置方案采用动态罚函数β 进行调整。算法迭代前期采用较小罚函数避免破坏种群多样性，迭代后期采用较大罚函数快速淘汰不满足约束个体使算法快速收敛，设计动态罚函数β 如下：

式中：g、gmax—当前和最大迭代次数；φ—惩罚因子，取φ=5。

若违反产品性能约束，则按式（14）调整。若违反成本约束，则按式（15）调整；若违反交货期约束，则按式（16）调整。

3.3 选择操作

首先对初始化的种群进行非支配排序和拥挤距离计算，然后采用二元锦标赛方法进行选择。

选择步骤如下：

（1）从父种群中随机选择2 个个体；

（2）判断两个个体的支配关系，将非支配个体添加到子种群，若两个个体互不支配，则跳到（3）；

（3）判断两个个体的拥挤距离，将拥挤距离大的个体添加到子种群，若拥挤距离相同，则随机选择一个个体添加到子种群；

（4）返回（1），并循环，直到子种群规模达到父种群规模一半，则算法终止。

3.4 交叉操作

算法迭代前期，应保持较大的交叉概率来扩大寻优范围，迭代后期为避免破坏较优个体应用较小交叉概率[9]，自适应交叉概率Pc如下：

式中：Pcmax、Pcmax—最大和最小交叉概率，取 Pcmax=0.9，Pcmin=0.6；g、gmax—当前和最大迭代次数。

式中：a、b—［0，1］区间上均匀分布的随机数。

3.5 变异操作

采用自适应交叉概率相似原理，设计自适应变异概率Pm。

式中：Pmmax、Pmmin—最大和最小变异概率，取 Pmmax=0.1，Pmmin=0.01；g、gmax—当前和最大迭代次数。

将交叉操作后的个体进行多项式变异得到新的个体。

3.6 模拟退火操作

采用改进的Metropolis 准则判断是否接受变异操作后的个体。由于Metropolis 准则无法对多目标问题的新解进行接受判断，因此需要对Metropolis 准则进行改进[10]。

设变异操作前后个体分别为vold、vnew，对应的第m 个目标的函数值分别为fm（vold）、fm（vnew），接受vnew的概率P 为：

式中：T0—初始温度，取 T0=100；T0—冷却系数，取 a=0.9；k—降温次数，即为迭代次数。

改进后的 Metropolis 准则说明：若 fm（vnew）＜fm（vold），则接受vnew；若 vnew和 vold互不支配，则同时接受 vnew和 vold；当 fm（φnew）＞fm（φold）时，若则接受 vnew，若＜rand 则不接受 vnew。

3.7 算法步骤

（1）参数设置，包括种群大小N，最大遗传代数gmax，初始温度 T0，冷却系数 a 等，初始化种群 P0，g=1；

（2）计算种群Pg的适应度函数值，对违反约束个体进行动态罚函数调整，并进行非支配排序和拥挤距离计算；

（3）通过二元锦标赛方法从种群中选择N/2 个个体，进行算术交叉和多项式变异操作，并按改进的Metropolis 准则接受新个体，得到子代种群；

（4）将父代Pg和子代种群合并，得到临时种群Rg，对临时种群Rg进行非支配排序和拥挤距离计算，采用精英保留策略选出N 个个体，得到新一代种群Pg+1；

（5）判断是否 g=gmax，否则返回（2），并 g=g+1，T=agT0；是则算法终止，输出满足约束的结果。

改进的NSGA-Ⅱ算法流程，如图1 所示。

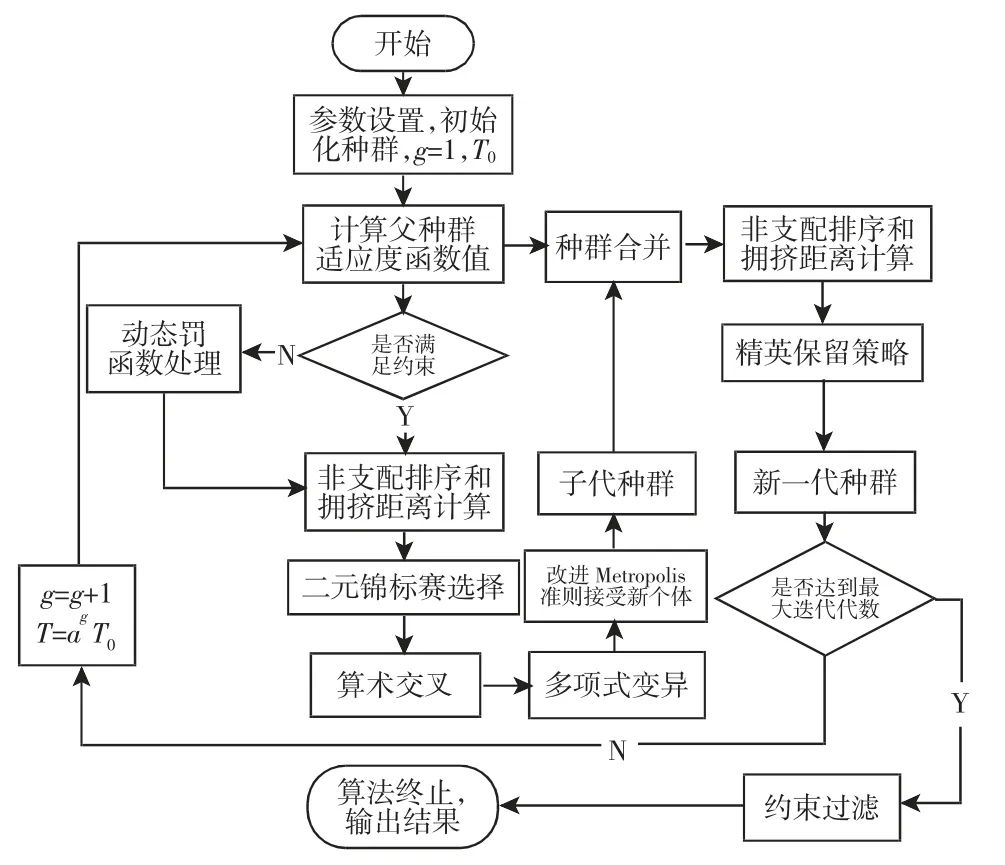
图1 改进的NSGA-Ⅱ算法流程Fig.1 Improved NSGA-ⅡAlgorithm Flow

4 产品配置方案推荐

根据顾客偏好对各产品配置目标赋予权重wi（i=1，2，3），并采用综合线性加权法计算第y 种产品配置方案的综合指标fy，将fmax对应的产品配置方案推荐跟顾客。

式中：Fy、Cy、Ty—第y 种产品配置方案对应的产品性能、成本和交货期目标函数值。

5 算法验证与实例应用

5.1 算法验证

采用文献[8]中的实验数据，以NSGA-Ⅱ算法为比较算法，设定交叉概率为0.9，变异概率为0.1，种群大小为100，最大迭代代数为100，最大交货期为75 天，最大成本为6000 元，企业利润率为0.15；仿真环境为Intel（R）Core（TM）i5-3210M，CPU@2.50GHz，RAM 6GB，系统Windows 10；仿真平台Matlab2015a。仿真结果，如表1 所示。各个目标函数变化曲线，如图2～图4 所示。

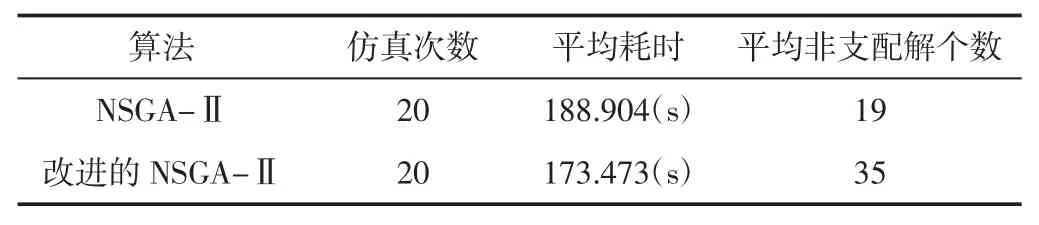
表1 仿真结果对比Tab.1 Comparison of Simulation Results

由表1 可知：改进的NSGA-Ⅱ算法比NSGA-Ⅱ算法求解问题平均耗时少，算法求解效率更高，且得到的平均非支配解个数更多，求解结果更好，算法对比优势明显。

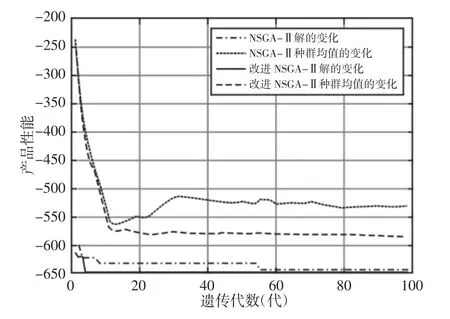
图2 产品性能目标函数变化曲线Fig.2 Product Performance Objective Function Variation Curve

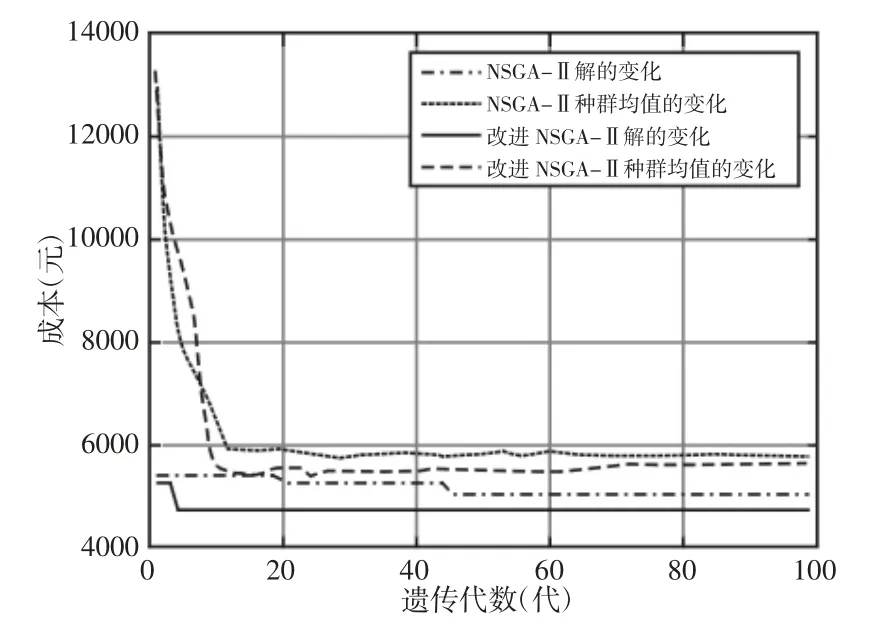
图3 产品成本目标函数变化曲线Fig.3 Product Cost Objective Function Variation Curve

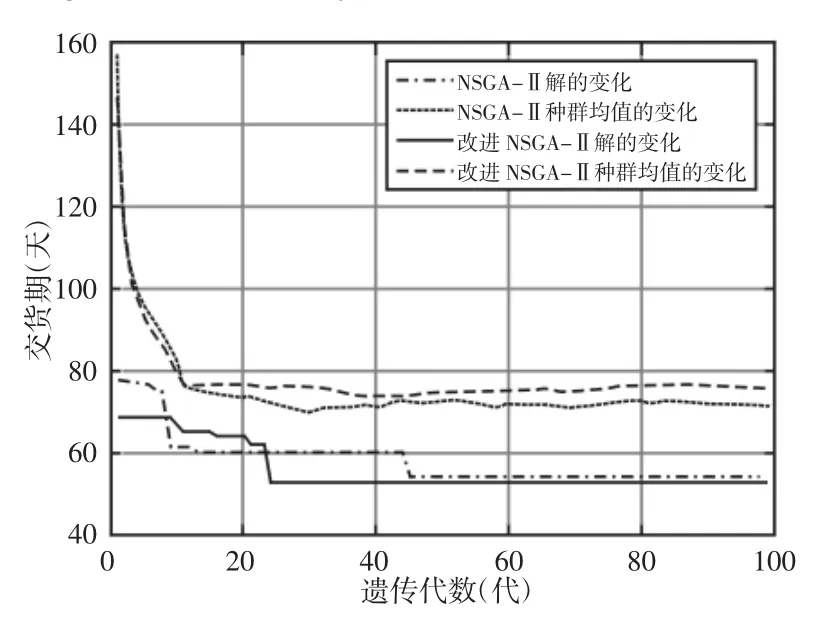
图4 产品交货期目标函数变化曲线Fig.4 Product Due Date Objective Function Change Curve

从图2～图4 可知，改进的NSGA-Ⅱ算法的各目标函数变化曲线收敛速度明显快于NSGA-Ⅱ算法，并且曲线的末端值更小，得到的解的质量更好。因此，改进的NSGA-Ⅱ算法在配置问题求解上优于NSGA-Ⅱ算法。

5.2 实例应用

某模块化产品族S，拥有4个必选配置单元和2 个可选配置单元，其零部件实例特征属性值，如表2 所示。顾客需求：产品性能至少600，最长交货期20 天，最高成本8000 元企业数据：装配成本系数50，装配工期系数0.5，企业利润率0.15，物流运输时间2 天；设置改进的NSGA-Ⅱ算法参数：种群大小100，最大迭代代数100。产品配置模型求解结果，如图5 所示。

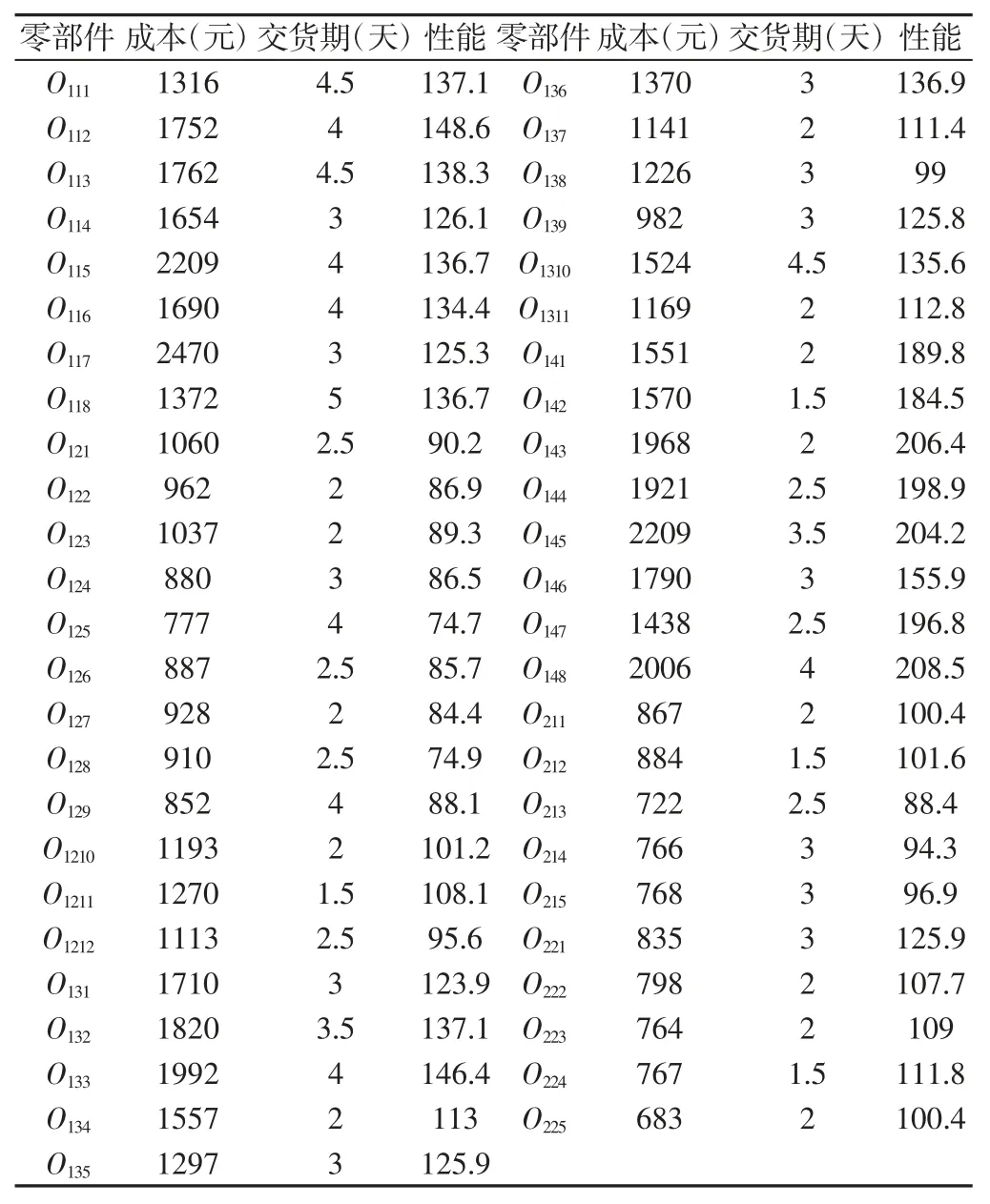
表2 零部件实例特征属性值表Tab.2 Component Example Feature Attribute Value Table

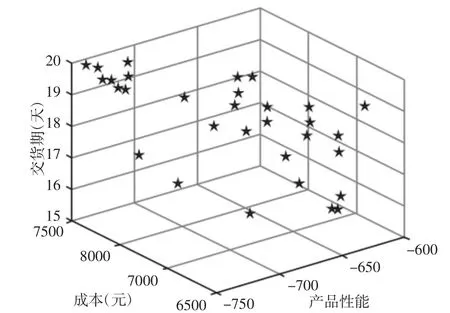
图5 产品配置模型Pareto 最优解集Fig.5 Pareto Optimal Solution Set of Product Configuration Model

仿真运行10 次，将求解结果合并去重，共得到78 个符合顾客需求的配置方案。

根据顾客偏好设定产品性能、成本和交货期目标权重，由式（21）计算得到推荐方案，如表3 所示。

表3 产品配置推荐方案Tab.3 Product Configuration Recommendation Scheme

6 结语

针对多目标产品配置优化问题，考虑个性化等约束，以产品性能最大化、成本和交货期最小化为目标建立产品配置模型，使得配置模型能够满足顾客的个性化需求；设计了一种改进的NSGA-Ⅱ算法求解配置模型，该算法采用自适应交叉和变异概率提高算法收敛速度，对变异操作结果进行模拟退火操作，避免了算法陷入局部最优解；根据顾客偏好推荐配置方案，避免顾客因配置方案过多导致的选择困难。

通过与NSGA-Ⅱ算法对比，证明改进NSGA-Ⅱ算法在配置问题求解上性能更优，具有一定理论意义；通过实例应用，证明本模型有效可行，具有一定的推广应用价值。