一种新的Sierpiński三角分形生成算法
赵向东,江瑶,马中华
一种新的Sierpiński三角分形生成算法
赵向东,江瑶,马中华
(天津职业技术师范大学 理学院,天津 300222)
介绍6向链码及Sierpiński三角分形相关基础理论,将6向链码技术应用于Sierpiński三角分形,提出了一种新的Sierpiński三角分形算法.与经典的Sierpiński三角分形算法相比,6向链码方法在构造经典分形图形——Sierpiński三角分形时,更易实现,效率更高.
6向链码;Sierpiński三角;分形
1 引言及预备知识
Sierpiński三角分形是分形几何中一种最典型的分形几何图形,是一种典型的自相似集三角分形,其广泛应用于化学分子结构、地毯构成、计算科学和工程等研究领域[1-4].
链码(又称为Freeman码)方法是美国学者Freeman于1961年提出的,是一种用于表示任意几何曲线构型的方法,其实质是一串指向符序列,用曲线起始点坐标和边界点方向符来描述曲线或边界的方法[5],常被用于计算机图形学和模式识别等领域[6-7].高荣华[8]等利用顶点链码的方法计算了区域的面积;王平[9]等基于Freeman链码提出了直线识别算法;刘勇奎[10]等研究了压缩链码;余博[11]等基于Freeman码方法提出了曲线匹配方法,其方法简单易于实现,且不受曲线旋转和缩放影响.
近年来,链码方法的研究和应用已相当成熟,文献[12]基于链码方法提出了串珠编织路径算法,文献[13]提出了Freeman链码技术的几何图形识别算法.因此,Freeman链码方法在处理图像图形学中有着广泛的应用价值.
常用的Freeman链码按照中心像素点邻接方向个数可分为4 向链码(见图1)和8向链码(见图2).
图1 4向链码

图2 8向链码
6向链码相比于4向链码和8向链码具有良好的连通性,且在图像处理算法中易于实现,因此,诸多学者也对6向链码进行了深入研究.刘勇奎[14]提出了6向链码上的椭圆生成算法、圆弧生成算法以及轮廓跟踪算法;文献[15]将6向链码应用于六边形的串珠编织路径中,并提出了相应的算法;文献[16]提出了基于6向链码的Koch曲线生成算法;文献[17]进一步深入研究了六边形网格链码方法.本文基于6向链码方法,提出一种新的Sierpiński三角分形算法,且和经典的Sierpiński三角分形算法——递归算法、D0L系统算法、多规则LS文法进行了对比,分析其程序运行效率.结果表明,新的算法更易实现,效率更高.
本文只给出6向链码及Sierpiński三角分形的定义,详细基础理论知识见文献[18-19].


图3 6向链码图

图4 6向链码串实例

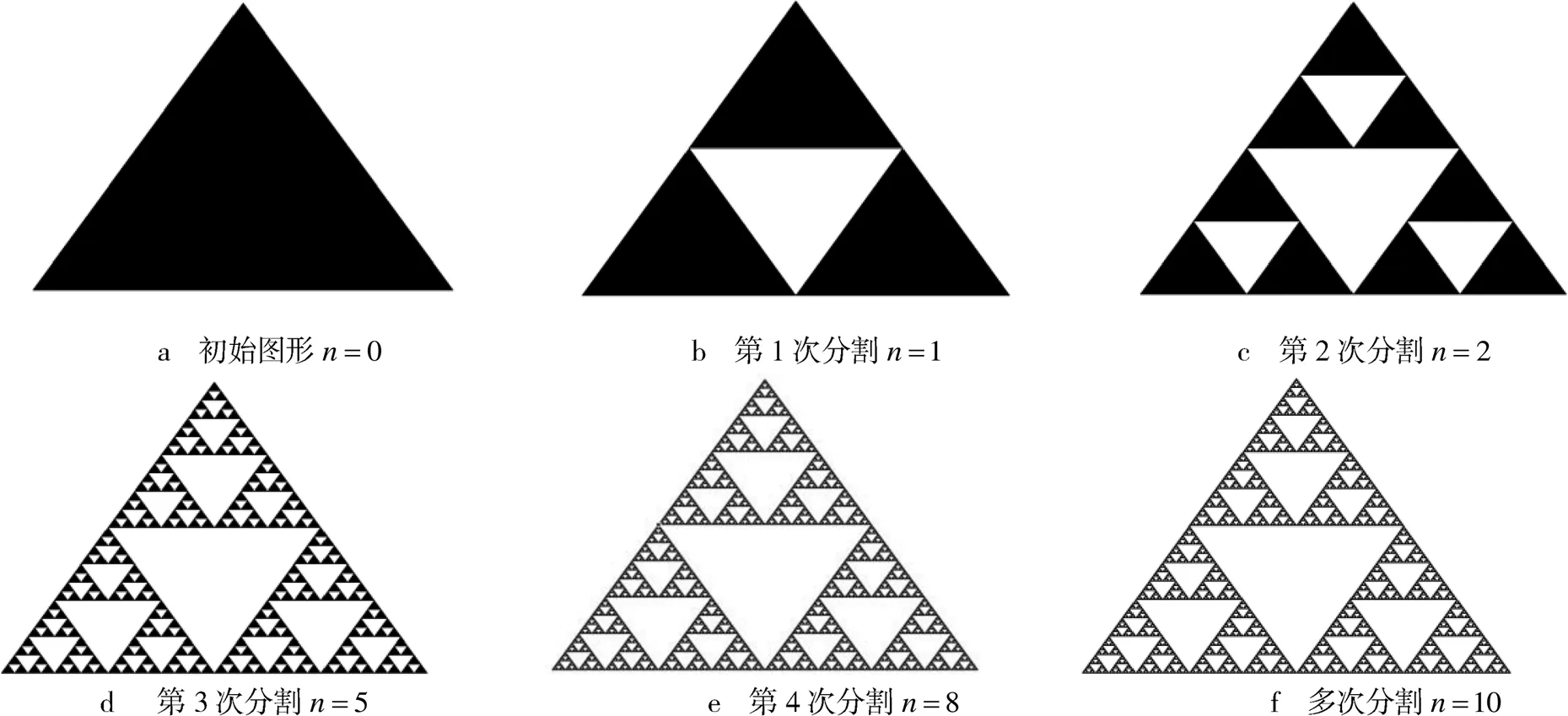
图5 Sierpiński三角分形生成过程
2 算法介绍
2.1 6向链码仿真Sierpiński三角分形算法描述

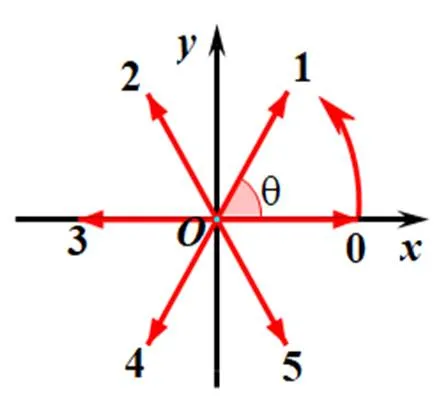
图6 6向链码和坐标之间旋转关系




基于6向链码法的Sierpiński三角分形算法步骤为:
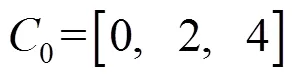
2.2 仿真实验结果
为了能够更好地确保算法的正确性,进一步地,可以利用经典的Sierpiński三角分形算法——递归算法,在相同的迭代次数下进行验证,其仿真结果与图7 一致(见图 8),主要区别是在相同迭代次数下迭代时间不同.

图7 6向链码法仿真Sierpiński三角分形

图8 递归算法仿真Sierpiński三角分形

图9 6向链码法()仿真Sierpiński三角分形
3 Sierpiński三角分形算法性能对比
在不同的迭代次数下,计算算法的平均运行时间,通过与递归算法[18]19、D0L系统算法[19]59对比,可分析得出6向链码法在绘制Sierpiński三角分形垫片时的性能(见表1).
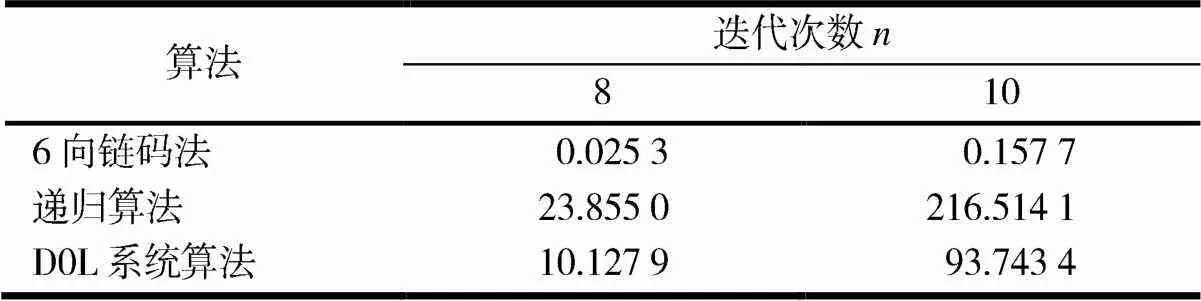
表1 6向链码法与经典算法性能对比 s

表2 6向链码法与多规则LS文法性能对比 s
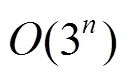
综上可知,6向链码法在绘制Sierpiński三角分形方面,具有容易实现,程序运行效率高的优点.
4 结语
本文介绍了6向链码,并将6向链码与经典分形几何图形——Sierpiński三角分形构造原理相结合,给出了一种新的基于6向链码技术构造Sierpiński三角分形的算法.为了更好地测试6向链码方法的性能,选取经典的Sierpiński三角分形算法——递归算法、D0L系统法以及多规则LS文法,在不同迭代次数下,对运行时间进行了对比分析,得出了6向链码在Sierpiński三角分形构造中的优势——易于实现,程序效率高.
[1] 张珍,谢文俊,杨奕,等.基于卤键的谢尔宾斯基三角分形自组装的模拟研究[J].物理化学学报,2017,33(3):539-547
[2] 王燕.基于谢尔宾斯基三角分形压电振子的性能研究[D].南京:南京邮电大学,2016
[3] 王丽.三分谢尔宾斯基垫片上的标准拉普拉斯算子[J].江苏理工学院学报,2014,20(6):13-17
[4] 王书颖,范钦杰.一类描述Sierpinski(谢尔宾斯基)垫的拟移位映射[J].吉林师范大学学报:自然科学版,2007(4):49-51
[5] Freeman H.On the encoding of arbitrary geometric configurations[J].IRE Transactions on Electronic Computers,1961(2): 260-268
[6] Freeman H,Davis L S.A corner-finding algorithm for chain-coded curves[J].IEEE Transactions on computers,1977(3): 297-303
[7] Freeman H.Computer processing of line-drawing images[J].ACM Computing Surveys(CSUR),1974,6(1):57-97
[8] 高荣华,张有会,曹清洁,等.顶点链码表示区域的面积计算[J].计算机应用与软件,2005,22(8):106-108
[9] 王平,董玉德,罗喆帅.基于Freeman链码的直线识别方法[J].计算机工程,2005,31(10):171-173
[10] 刘勇奎,魏巍,郭禾.压缩链码的研究[J].计算机学报,2007,30(2):281-287
[11] 余博,郭雷,赵天云,等.Freeman链码描述的曲线匹配方法[J].计算机工程与应用,2012,48(4):5-8
[12] 闫建业,姚立纲,林冬良,等.串珠凉垫编织路径数学建模与仿真[C]//第10届中国机构与机器科学应用国际会议(2013CCAMMS)论文集. 北京: 中国机械工程学会机械传动专业学会机构学专业委员会,2013:249-253
[13] 裴姗,章腾.基于 Freeman 链码的几何图形识别算法[J].计算技术与自动化,2018(3):21-25
[14] 刘勇奎.计算机图形学的基础算法[M].2版.北京:科学出版社,2007:164-183
[15] Zhao X,Sun W,Liu X,et al.On Six Directions Chain Code and Its Application of Bead Weaving[C]//2018 IEEE 4th International Conference on Computer and Communications(ICCC).成都:四川省电子学会,2018:2262-2267
[16] Liu X,Ma Z,Zhao X.A Comparison of Algorithms of Drawing the Koch Snowflake Curve[C]//Proceedings of the 3rd International Conference on Computer Science and Application Engineering.New York:Association for Computing Machinery,2019:1-5
[17] 魏小峰,苗双喜,濮国梁,等.应用于六边形网格的链码方法[J].武汉大学学报:信息科学版,2019,44(11):1700-1707
[18] 孙博文.分形算法与程序设计——Visual C++实现[M].北京:科学出版社,2004
[19] 朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011
A new algorithm for generating Sierpiński triangle fractal
ZHAO Xiangdong,JIANG Yao,MA Zhonghua
(School of Science,Tianjin University of Technology and Education,Tianjin 300222,China)
The basic theory of six direction chain code and Sierpiński triangle fractal correlation are introduced,a new Sierpiński triangle fractal algorithm is proposed by applying the six direction chain code technique to Sierpiński triangle fractal.And compared with the classical Sierpiński triangle fractal algorithm,the six direction chain code method is easier to be implemented and more efficient in constructing the classical fractal graph——Sierpiński triangle fractal.
six direction chain code;Sierpiński triangle;fractal
O189.11
A
10.3969/j.issn.1007-9831.2020.06.002
1007-9831(2020)06-0005-05
2020-04-10
国家自然科学基金项目(11601391);天津市自然科学基金项目(18JCQNJC69700);天津市高等学校科技发展基金计划项目(JWK1611);天津职业技术师范大学研究生创新基金项目(YC19-36)
赵向东(1993-),男,甘肃庆阳人,在读硕士研究生,从事计算代数几何研究.E-mail:zxdtute17010@tute.edu.cn

