高原环境连续下坡路段制动鼓温度预测模型

陈立辉, 郭忠印

(1.同济大学道路与交通工程教育部重点实验室，上海 201804； 2.东华理工大学土木与建筑工程学院，南昌 330013)

高原环境连续下坡路段，大货车不仅受连续下坡恶劣道路条件的影响，还要受高原低压缺氧恶劣环境条件的影响，道路安全形势更加严峻.

大货车在连续下坡路段的主要事故原因是制动器“热衰退”导致的制动失灵[1-2]. 温度过高是制动器发生“热衰退”的主要原因[3]. 为了得到大货车在连续下坡路段的制动器温度预测模型，国内学者[4-9]根据连续下坡路段的坡度、坡长、载重、车速等因素对制动鼓温度的影响，通过试验采集相关数据，利用回归分析方法得到制动鼓温度预测模型. 然而，这些基于回归分析得到的温度预测模型参数过少，难以适应各种条件下的制动器温度特征，如车速、环境温度、辅助制动、海拔高度等对制动器温度产生的影响，过少的变量导致模型的通用性较差. 为了弥补回归分析法的不足，同济大学的杜博英等[10]利用能量守恒理论建立了连续下坡路段货车制动鼓变速温度预测模型，并且通过野外试验和数理统计方法对模型的部分参数进行了标定和修正. 世界道路协会根据能量守恒定律和牛顿冷却定理，理论推导出了连续下坡路段的制动鼓温度预测模型[11]. 以上2种理论推导模型逻辑严密，但变量需要根据不同环境条件进行修订.

高原环境对制动器热衰退的影响主要是通过对车辆辅助制动装置的影响实现的. 发动机辅助制动系统是一种有效的辅助制动方式，其原理类似于空气压缩机，将发动机由输出动力装置变为消耗动力装置，再通过将下坡路段的机械能转化为发动机内的气体内能，并在发动机排气冲程中将高温气体排入外环境，从而实现控制或降低车速的目的[12]. 在高海拔地区，大气密度随海拔高度升高而减小，发动机辅助制动系统靠压缩空气吸收外部导入能量的这种工作方式，其制动效能会受大气密度的影响，进而影响主制动系统的使用强度，从而影响大货车在连续下坡路段制动器“热衰退”程度，最终影响连续下坡路段避险车道的设置，为连续下坡路段的道路交通安全带来隐患.

为了满足高原环境连续下坡路段安全保障措施设置对大货车制动器温升预测的需要，本研究在世界道路协会制动鼓温度预测模型基础上，通过引入海拔修正系数，对原有温度预测模型进行了修正，构建了适合各种海拔高度的连续下坡路段制动鼓温度预测模型.

1 理论分析

1.1 制动器热力学分析

在鼓式制动器制动过程中，假设输入其内部的能量全部转化为内能，其能量为Q，辐射换热量和对流换热量分别为Q1和Q2. 设制动鼓质量为mdr，其比热容为c，则制动鼓温升计算式为

(1)

1) 摩擦生热量

制动器的制动衬片与制动鼓之间在压力作用下，两者之间发生相互滑动摩擦产生热量，摩擦生热量计算式为

Q=μF1S

(2)

式中：μ为制动器摩擦因数；F1为制动衬片与制动鼓之间竖向等效压力；S为制动衬片与制动鼓之间的相对滑移距离.

2) 辐射散热

鼓式制动器独特结构设计使制动鼓与轮辋之间近似形成一个封闭的辐射散热系统，根据辐射换热理论和制动器参数推导出辐射散热公式为

(3)

式中：T为制动鼓外表面温度，℃；Ta为外环境温度，℃；σb为黑体辐射常数，又称斯蒂芬- 玻尔兹曼常数，一般取σb=5.67×10-8W/(m2·K4)；A、A1分别为制动鼓的外表面面积和轮辋的内表面面积；ε1、ε2分别为制动鼓材料和轮辋材料的黑度；t为制动时间.

3) 对流散热

对流换热是鼓式制动器最主要的散热方式，鼓式制动器的结构特点使制动器室与外界近似隔绝，可以通过牛顿冷却定律推导制动器的对流散热，具体公式为

Q2=hA(tw-tf)Δτ

(4)

式中:h为对流换热系数，W/(m2·℃);A为制动鼓外表面面积，m2；tw、tf分别为制动鼓外表面温度和接触空气温度，℃.

1.2 制动鼓温度预测模型

根据能量守恒定律，在连续下坡路段，车辆减少的机械能一部分用于克服滚动阻力、空气阻力、发动机制动阻力，剩余部分通过摩擦生热的形式转化为制动鼓的热力学能，部分热力学能又通过传导、辐射和对流形式散热，剩余部分在制动鼓和摩擦片内部积聚，并以制动器温度的形式表现出来.

3种散热形式中，对流换热是最主要的散热方式，约占总散热量的80%[13]，为简化计算，本文在建模过程中只考虑对流散热形式，其他散热量以修正系数的形式体现. 由于制动片的导热性能较差，热容量也比制动鼓小得多，因此在计算中可以认为摩擦热全部被制动鼓吸收，且因为制动鼓厚度较薄，可以认为制动鼓受热均匀，温度沿制动鼓壁厚方向无变化[14].

牛顿冷却定律是处理温度变化问题的常用方法，适用于强对流和温差不太大时的工况[15]. 通过牛顿冷却定律与能量守恒定律可以建立制动器温度方程

cmdrdT/dt=PB-hAc(T-Ta)/ω

(5)

式中：c为制动鼓比热容，c=0.482 kJ/(kg·℃)；Ac为制动鼓有效散热面积，Ac=0.39 m2；PB为制动鼓吸收功率，W；h为制动器对流换热系数；mdr为制动鼓质量，mdr=80.05 kg；Ta为外界环境温度，℃；T为制动鼓预测温度，℃，为时间t的函数；ω为对流散热量占总散热量的比例，本文取0.8. 式(5)化为微分方程的形式后，可得

T′+k1T-k1(Ta+k2PB)=0

(6)

当t=0时，T=T0，将此边界条件带入方程即可得到连续下坡路段制动鼓温度预测模型

T(t)=T0e-k1t+Ta(1-e-k1t)+k2PB(1-e-k1t)

(7)

式中：T0为制动鼓初始温度，℃；t为车辆运行时间，s；k1为热时间参数的倒数，k1=(hAC)/(cmω)；k2为总传热参数的倒数，k2=ω/(hAC).

根据车辆受力分析可得制动鼓吸收功率

(8)

式中：PG为重力对货车做功的功率，kW；Pa为空气对车辆做功的功率，kW；Pr为滚动摩擦力对车辆做功的功率，kW；Pab为发动机制动系统对车辆做功的功率，kW；β为制动力分配系数；s为车辆在路面上的滑移率，滚动摩擦计算时，滑移率取0.

高原环境大气压力及空气密度随海拔高度而变化，导致车辆空气阻力和发动机制动阻力发生变化. 发动机制动功率大小通过制动效率来衡量，制动效率指的是发动机制动时产生的负功相对于发动机做正功最大功率的百分比，

Pab=kP0

(9)

式中：k为发动机制动效率系数；P0为转速对应最大正功率.

本研究试验车辆的发动机为东风公司的dci11型号，该型号采用了皆可博公司的顶置式制动鼓. 根据皆可博公司在东风公司考核点的该款发动机制动试验数据，发动机转速1 600转时的制动功率为133 kW；额定转速1 900转时的制动功率为190 kW；转速2 200转时的制动功率为261 kW. 额定转速1 900转时的辅助制动功率为190 kW，与该转速下的额定正功率276 kW相比，制动效率约69%. 发动机转速与制动功率近似成线性关系为

Pab=0.213 3n-210.67

(10)

本研究通过VBOX 3i设备连接发动机ECU接口采集发动机相关数据，包括发动机的转速、扭矩、水温等，也可以通过另外一个公式获得发动机的转速

n=uaigi0/(0.377r)

(11)

式中：ua为车速；ig为相应档位传动比；i0为主减速比；r为车轮半径.

从式(10)中可以看出，转速越快，辅助制动效果越好，当转速为≤987 r/min时，发动机辅助制动功率为0，发动机失去制动能力.

发动机制动的本质是利用发动机压缩冲程产生的压缩阻力、内摩擦力和进排气阻力对驱动轮形成制动作用，空气密度是影响压缩阻力的主要因素之一，空气密度随海拔高度升高而下降，因此，高原环境发动机制动效率需要考虑海拔修正系数.

1.3 海拔修正系数

发动机制动的本质是通过做功的形式将车辆的机械能转变为发动机气缸内气体的内能，根据热力学第一定律，封闭系统内的内能变化可以表示为[16]

ΔU=Q+W

(12)

式中：ΔU为内能变化量；Q为从外环境吸收的热量；W为外界对系统的做功.

由式(12)可知，系统内能的增加有2个途径：一是从外界环境吸热，另一途径是外界对系统做功，因为车辆对发动机气缸内气体不做非体积功，因此

W=-ΔU

(13)

根据理想气体状态方程，车辆在连续下坡路段匀速行驶时，不同海拔高度下的理想状态方程为

(14)

当压缩体积一定时，压缩气体提供的反作用力取决于气体的摩尔数及封闭系统内的温度，不同海拔环境下发动机气缸内气体提供的反作用力比值为

p1/p2=(n1T1)/(n2T2)

(15)

通过式(15)可以知道，确定p1、p2的比值，需要确定T1与T2和n1与n2的关系，进气量受大气密度影响，气缸内气体温度受气缸壁温度影响，因发动机散热系统主要是通过循环水进行冷却，因此通过水温即可知道发动机缸壁的温度情况.

为此，本研究通过测量连续下坡路段发动机水箱的温度来确定气缸内气体的环境温度，以下所示为最高海拔高度4 800 m的巴颜喀拉山和最高海拔高度3 400 m的日月山2个试验段水箱温度随坡长变化.

1) 巴颜喀拉山试验段

巴颜喀拉山段连续下坡路水箱温度与坡长关系，如图1所示.

2) 日月山试验段

日月山试验段发动机水箱温度和坡度关系，如图2所示.

从以上试验数据可以发现，试验车辆的发动机水箱温度随坡长的增加而不断下降，巴颜喀拉山试验段的水箱最后稳定温度约为78 ℃，日月山试验段的水箱最后稳定温度约为79 ℃，2个试验点的最后稳定温度相差不太明显，因此可以认为，2个试验点的发动机气缸外温度相同，即不同海拔高度连续下坡路段，发动机气缸外环境温度相同，因此可以得到

(16)

式中：ρ1为海拔高度为H1时对应的空气密度；ρ2为海拔高度为H2时对应的空气密度；k′为不同海拔高度的发动机制动效率.

因此，发动机辅助制动系统对车辆做功的功率表示为

Pab=k′kP0

(17)

式中：k为低海拔环境下发动机制动效率；k′为发动机制动效率海拔修正系数；P0为该转速对应最大正功率.

制动器吸收功率

(18)

从式(16)可知，海拔高差越大，海拔修正系数越小，则制动鼓吸收功率越大，意味着制动鼓温度升高幅度越大.

为了验证制动鼓温度预测模型的有效性，本研究选择高原地区2个连续下坡路段，通过实车试验的形式，来检验温度预测模型的准确性和通用性.

2 试验设计

2.1 试验路段

本研究以国道G214青海省境内最高海拔高度分别为3 400、4 800 m的日月山和巴颜喀拉山连续下坡路段为试验路段进行制动器温升试验，其中日月山长大纵坡路段是2003年公安部和国家安全生产监督管理局确定的29处危险路段之一，多次进入全国十大危险路段名单. 与此同时，选择同海拔高度长直线路段进行拖档滑行试验. 长直线路段包括日月山试验点和巴颜喀拉山试验点附近海拔高度近似的长直线试验路段.

2.2 试验设备

选择具有发动机辅助制动系统的总质量49 t东风天龙(DFL4251A9)牵引车为试验车型，选择VBOX 3i作为数据采集设备，如图3所示，利用埋入式温度传感器，通过在制动片侧面打孔的形式，将温度传感器埋入制动片采集制动片温度数据，如图4所示. 选择驾龄5 a以上的本地驾驶员以自然驾驶方式进行试验. 为了保证实测数据的可靠性，本试验通过多次重复试验的方式进行相互验证.

选择对制动片温升最不利的夏季7—8月作为试验月份，白天早上8点到下午4点的晴朗天气作为试验时段.

2.3 制动器温度试验

利用VBOX 3i主机以及温度传感器，双向采集连续下坡路段制动器温度及其他相关数据，主要包括纵坡坡度、坡长、海拔高度、车速、环境温度、制动片温度等数据.

利用VBOX 3i主机的CAN接口，连接发动机ECU端口，采集发动机转速、水箱温度等相关数据.

2.4 脱档滑行试验

通过汽车脱档滑行试验来确定滚动摩擦因数. 在长直线路段，将试验车辆加速到预定车速，然后快速摘档，使车辆滚动滑行到停止，记录过程中行驶的距离、速度、时间、高差等数据，最后通过数据处理，得到距离随时间变化曲线.

2.5 试验测试流程

为了明确试验测试过程，以及相关的试验设备及采集的主要数据，根据制动器温度试验和拖档滑行试验，汇总测试传感器、安装位置、数据采集装置等信息. 绘出试验测试框图，如图5所示.

3 参数确定

3.1 大气相关参数

1) 空气密度

随着海拔高度的升高，大气压和大气密度随之下降，海拔高度与空气密度近似线形关系，不同海拔高度的空气密度可以通过插值的方法得到.

空气密度、大气压随海拔高度变化情况如表1所示.

表1 空气密度、大气压与海拔高度关系表

2) 空气阻力系数

风阻系数主要与物体的形状有关，确定风阻系数的主要手段是风洞试验，根据相关文献的研究成果[17]，大货车的风阻系数为0.7～0.8. 本文取风阻系数Cd=0.7.

3.2 滚动摩擦因数

1) 日月山段路面滚动摩擦因数

根据以上分析，可以得到日月山试验段路面滚动摩擦因数，如表2所示.

对3次试验结果取均值后，日月山试验段路面滑动摩擦因数为μr=0.008 47.

表2 日月山试验段路面滚动摩擦因数

2) 巴颜喀拉山段路面滚动摩擦因数

与日月山段的分析过程类似，可以得到巴颜喀拉山试验段的路面滚动摩擦因数，如表3所示.

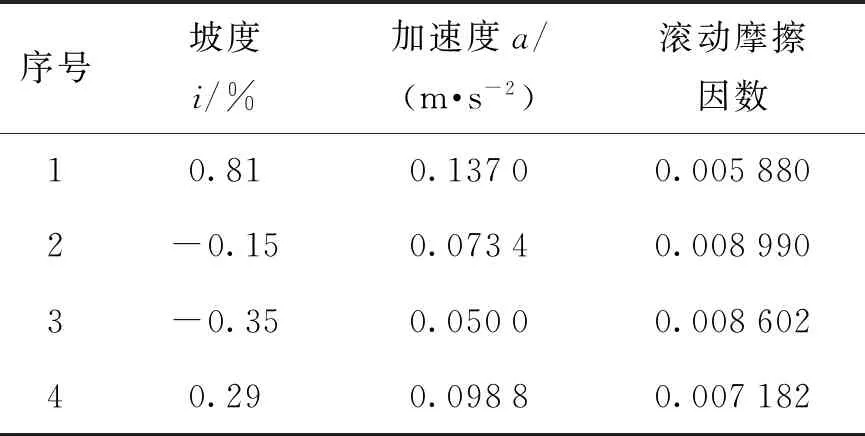
表3 巴颜喀拉山试验段路面滚动摩擦因数

对该试验段的4次试验结果取均值后，巴颜喀拉山试验段路面滑动摩擦因数为μr=0.007 66.

3.3 对流换热系数

根据采集到的数据，依据牛顿散热定律，制动鼓温度变化率ΔT/t与制动鼓终点温度T与环境温度Ta的差值的比值，即可得到各试验路段对流换热系数h值，将其代入热时间参数倒数k1和总传热参数倒数k2，即可得到k1和k2值，如表4所示.

表4 制动器对流换热系数

3.4 制动力分配系数

两轴汽车的制动力分配系数一般为定值，多轴汽车则较为复杂[18]. 车辆在制动过程中，根据制动时汽车的受力分析[19]可知，地面对不同轮轴的反作用力并不相同. 对于双轴汽车，车辆在制动过程中出现3种后果[20]，第1种情况，前轮先抱死拖滑，然后后轮抱死拖滑，这种情况会导致车辆丧失转向能力；第2种情况，后轮先抱死拖滑，然后前轮抱死拖滑，这种情况可能导致后轴出现侧滑；第3种情况，前后轮同时抱死拖滑，这种情况对制动安全最有利. 因此，制动力分配比例会影响车辆制动时的方向稳定性和附着条件利用程度.

本研究的试验车型为东风天龙六轴拖挂车，轴距分布如图6所示.

该试验车辆为六轴拖挂车，制动力分配较为复杂，难以通过公式计算，为了确定各个轮轴之间的制动力分配系数，本研究通过试验方法来确定制动力分配系数，从前往后数第3轴和第4轴的左右2个制动器在下坡路段温度随时间变化情况如图7所示.

通过分析制动器单位时间温度的变化率，即可知道单位时间输入制动器的制动功率的大小，因为制动功率分配的越多则温度升高的幅度越大，进而可以得到制动力分配系数.

通过对以上数据进行线形拟合可以得到4个制动器的温度变化率拟合方程，以下方程分别为四轴左侧、四轴右侧、三轴左侧、三轴右侧制动器的温度随时间变化方程

y=0.349 4x+78.846R2=0.993 3
y=0.299 7x+52.447R2=0.997 6
y=0.041 9x+42.721R2=0.992 6
y=0.035 6x+45.171R2=0.996 6

式中：x为时间；y为温度.

方程系数为温度随时间变化率，也是单位时间制动力分配分布比例. 从轴距分配图可知，后三轴4、5、6轴制动力分配系数相同，重载车辆的制动力分配系数主要分配到后轴，且重心越靠后这种趋势越明显[21]，从拟合方程可以近似得出三轴和四轴的动力分配系数约为1：8.4，前三轴1、2、3轴制动力分配系数近似相同，取相同制动力分配系数，因此可以得到四轴制动力分配系数约为0.3.

4 模型验证

为了保障制动器温度模型的可靠性，选择巴颜喀拉山和日月山两处试验路段进行温度预测模型的实车试验. 根据道路、车辆、车速及制动鼓温度等相关试验数据，得到制动力分配系数、对流散热系数、滑动摩擦因数等相关参数值，代入制动鼓温度预测模型即可得到制动鼓温度的预测值，其中，对流散热系数分别采用对应试验路段的参数值. 将制动鼓的测量温度与预测温度进行比较，如图8所示，其中横坐标为试验次数序号，巴颜喀拉山试验段进行了15次试验，日月山试验段进行了12次试验，纵坐标为温度，℃，图例中基准温度是海拔高度为0时的制动器温度，此时，发动机制动效能未折减.

从图8中以看出，预测值和测量值之间的趋势符合程度较好，巴颜喀拉山试验段海拔更高，则预测温度与基准温度温差更大，相对来说，日月山试验段海拔高度较巴颜喀拉山试验段海拔高度小，预测温度与基准温度温差小一些. 为了从数值上评价预测值的精度，通过误差公式

(19)

来进行评估. 将具体的数值带入式(19)，得到表5所示的比较表.

巴颜喀拉山段温差均值P≈-6.8%，预测值与实际值相比平均偏小约6.8%；日月山段温差均值P≈3.7%，预测值比实际值偏大约3.7%. 综合2个试验段的温差结果，温度预测误差可以控制在7%以内，可以认为模型误差在可接受范围.

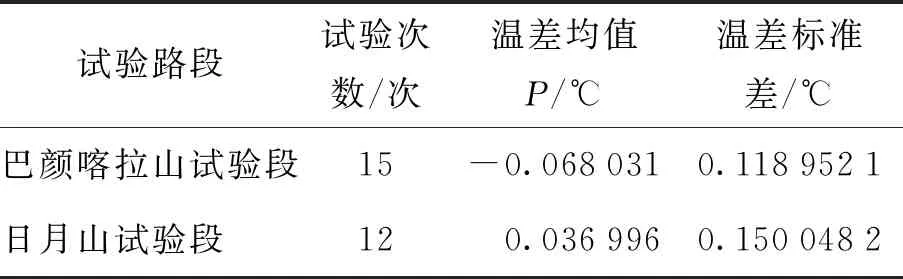
表5 制动鼓实际温度与预测温度比较表

5 结论

1) 根据制动器温升理论可知，不同环境条件下，影响制动器温度的主要因素不同，在高原环境下，高原因素对制动器温度的影响不容忽视，且海拔高度越高影响越大.

2) 高原环境是通过间接形式影响制动器的温度，即通过影响大货车发动机辅助制动系统的制动效能，进而影响车辆主制动器的使用强度，海拔高度越高，发动机辅助制动效能下降越多，则主制动器的使用强度越大，输入制动鼓内的能量越多，导致制动器“热衰退”越严重，制动器失灵的风险就越高.

3) 大型货车制动器温度是选择连续下坡路段避险车道位置的一个重要依据，高原环境使大型货车，尤其是大型重载货车的制动器热衰退程度更严重，则避险车道位置的选择需要比低海拔环境下更靠近坡顶，不同海拔高度连续下坡路段避险车道位置的选择需要考虑海拔高度的影响.