高中物理动态电路的两种题型及其解法探析

陈兴敏 宋谋胜 陈琳

10.3969/j.issn.1671-489X.2020.21.100

摘  要 分析高考物理恒定电流中常见动态电路的两种题型及其解决方法，即通过滑动变阻器的改变来判断电路中I和U的变化趋势、U/I和ΔU/ΔI比值的变化等，具有简单、快速、准确的效果，对培养学生的物理学科探究精神和数理结合思维具有较高的教学价值。

关键词 高中物理;动态电路;数理结合;数形结合;物理学科素养

中图分类号：G632    文献标识码：B

文章编号：1671-489X（2020）21-0100-03

1 前言

动态电路分析是高中物理电学中的重要知识点，也是高考中的常见考点。它要求学生具备较深的物理基础知识和较高的探究思维能力与推理演算能力，也要求学生具备扎实的数学基本功，对培养学生的物理学科素养和数理结合思维具有重要的教学价值。高中物理动态电路通常指由于电路中的局部电阻变化（通常为滑动变阻器的阻值改变）而引起干路或支路中的其他电学量（如R总、U、I、P）发生相应变化的一类电路，其中分析尤以电路中I与U及其比值变化、ΔI和ΔU的比值变化等问题较为常见[1]。通常，学生在处理此类问题时以常规方法为主，分析中头绪多、过程杂、演算多而易出错[2]。实际上，对动态电路中物理量的比值变化分析如采用数形结合思想来探究处理则效果更佳。

由于高中物理动态电路以滑动变阻器构成的动态模型居多[3]，因此针对此动态电路模型，本文分析动态电路中常见两种题型的解答技巧，从而为高中物理动态电路的教学探究和高考动态电路试题的快速解答提供一定的参考。

2 题型与解法探析

题型一：判断电路中I和U的变化  高考中常出现判断动态电路中的I、U变化的题型，或先分析I、U变化，而后判断其他物理量如功率P变化的题型，主要考查学生是否掌握动态电路分析的逻辑思维方法。这类题如果采用常规的思维与处理方法，不仅步骤繁杂耗时，涉及较多的公式识记和过程演算，而且一旦某一环节出错，就会导致最终结论错误。

其实在实际分析中可利用“串反并同”规律来简单、快速、准确地判断出动态电路中各用电元件的两端电压U和通过电流I的变化情况。“串反并同”判据是指动态电路中某一器件的电阻增大（或减小）时，与它串联或间接串联的其他器件中的电流、两端电压均作与之相反趋势的改变，即减小（或增大）;而与它并联或间接并联的其他器件中的电流、电压均作与之相同趋势的改变，即增大（或减小）[4]。

在判断出I、U的变化后，可进一步判断器件功率的变化情况。

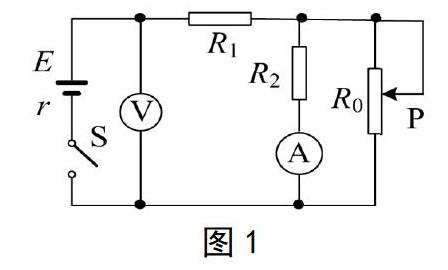
例1：（2011年高考北京卷第17题）[5]如图1所示电路中，电源内阻不可忽略。开关S闭合后，在变阻器R0的滑动端向下滑动的过程中（  ）

A.电压表与电流表的示数都减小

B.电压表与电流表的示数都增大

C.电压表的示数增大，电流表的示数减小

D.电压表的示数减小，电流表的示数增大

【解析】该题按常规思路需先分析总电阻、总电流的变化，再分析电源内阻所分电压、路端电压、R1所分电压、R2所分电压的变化关系，最终得出电压表与电流表的变化情况，如此步骤复杂、推演较多而致耗时易错。实际上该题完全可简化处理，因滑动变阻器的滑片P下滑时很明显其有效阻值R0↓，由于电流表A、电压表V均与R0为并联关系，根据“串反并同”判据，电压表的示数U↓，电流表的示数I↓，于是可快速准确地判断出选项A正确。

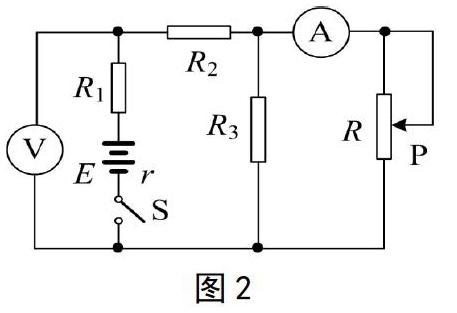
例2：如图2所示电路中，电源的电动势为E，内阻为r，当变阻器R的滑片P向上移动时，电压表V的示数U和电流表A的示数I的变化情况是（  ）

A.U变大，I变大

B.U变小，I变小

C.U变大，I变小

D.U变小，I变大

【解析】本题相比于例1在干路上多串联了一个定值电阻R1，如此使得电压表所测并非外电路的路端电压，但电压表V仍然与滑动电阻器R为间接并联关系。另外，电流表A则与变阻器R直接串联，故当滑动变阻器滑片P上移时，其阻值R↑，于是根据“串反并同”规律可得，电压表V的示数U变大，电流表A的示数I变小，从而快速简便地得出选项C正确。

可见，在电源内阻不能忽略时，运用“串反并同”的口诀能简单快速地获得正确结果，避免了繁杂的公式识记与过程推演。

題型二：判断电路中U/I和ΔU/ΔI的比值变化  动态电路问题中判断相关元件U/I或ΔU/ΔI的比值变化也是近年高考关注的考点。这类题型具有很强的迷惑性，易导致学生思路混乱而难以下笔。对于这类题型，可运用等效法原则，在电源内阻不能忽略的情况下，采用欧姆定律和数形结合的思想来等效处理动态电路中U/I或ΔU/ΔI的比值变化。

对于U/I的比值变化情形，根据欧姆定律U/I=R，即某元件任何时刻的U/I比值等效于该元件的电阻值，它表明无论该元件的U、I如何变化，其电阻值R的变化决定了U/I比值的变化。

如图3所示，一定值电阻R1与一滑动变阻器R2串联，电压表V1、V2分别测R1、R2的两端电压U1、U2，电流表A则测试整个电路中的电流I。当变阻器滑片滑动时，对不同用电元件利用欧姆定律有U1/I=R1、U2/I=R2、U外/I=（U1+U2）/I=

R1+R2。这表明经由R1、R2的变化，就能等效地判断出各元件的U/I比值变化情况，而通常各元件电阻的改变情形可快速准确地作出判决。在实际电路中，尽管变阻器阻值不断变化，但其U2/I的瞬时比值同步等于其阻值R2的瞬时值。

对于ΔU/ΔI的比值变化则需分两种情况处理。

第一种，当ΔU、ΔI所测为定值电阻元件的电压改变量和电流改变量时，则ΔU/ΔI=U/I=R测。考查正比例函数y=kx，其中斜率k=Δy/Δx=y/x，可见ΔU/ΔI=R测具有等效于数学上正比例函数的斜率意义而为定值。如图3中ΔU1/ΔI=

R1即为恒值。

第二种，当ΔU、ΔI所测为变化电阻元件的电压改变量和电流改变量时，如图3中测滑变电阻器R2的电压U2和电流I。由于滑动变阻器接入电路有效阻值R2的改变，R2端电压U2与通过其电流I的解析关系满足闭合电路的欧姆定律U2=E-（R1+r）I。如图4所示，该式U2（I）即为一次函数y=kx+b（截距为b、斜率为k=Δy/Δx），其图像截距为电源电动势E，斜率绝对值则为（R1+r）。它表明ΔU2/ΔI≠R2，

而是，它具有等效于数学上一次函数的斜率意义而为定值。ΔU、ΔI所测本为可变电阻元件的电压与电流改变量，但通过表达式及其图像分析表明，ΔU2/ΔI比值却与所测元件的电阻变化完全无关，而是等于除所测元件以外的其他器件（包括电源）的电阻值之和。

总之，以上两种情况表明，无论ΔU、ΔI所测是定值电阻元件，还是可变电阻元件的电压、电流改变量，二者的比值ΔU/ΔI则通常为定值。

例3：（多选）如图5所示，电路中的电表均是理想电表，电源内阻不能忽略，在滑动变阻器R1的滑动头从某处向下移动一小段的过程中，电表V1、V2、A的示数分别是U1、U2、I，电表V1、V2、A示数的变化量分别为ΔU1、ΔU2、ΔI，则下列说法正确的是（  ）

A.U2与I的比值不变，U2与I的乘积减小

B.U2与I的比值增大，U1与I的乘积一定增大

C.ΔU2与ΔI的比值等于任何时间U2与I的比值

D.ΔU1与ΔI的比值等于ΔU2与ΔI的比值

【解析】由图可见，滑动变阻器R1与定值电阻R2为串联关系，电压表V1、V2分别测R1两端的电压U1和R2两端的电压U2，电流表A测电路中的电流I。当滑动变阻器的滑动头开始向下移时，变阻器的有效阻值R1↑，利用“串反并同”判据，可得U1↑、U2↓、I↓。由于R2是定值电阻，根据题型二的第一种情况可知U2/I=ΔU2/ΔI=R2恒定不变，而P2=U2I减小，但P1=U1I的变化趋势不明确，故A、C正确，B错误。因为R1是可变电阻，根据题型二的第二种情况分析，ΔU1/ΔI的比值为所测可变电阻R1以外的其他所有电阻之和，即有ΔU1/ΔI=（R2+r），明显不等于ΔU2/ΔI的比值R2，故D错误。

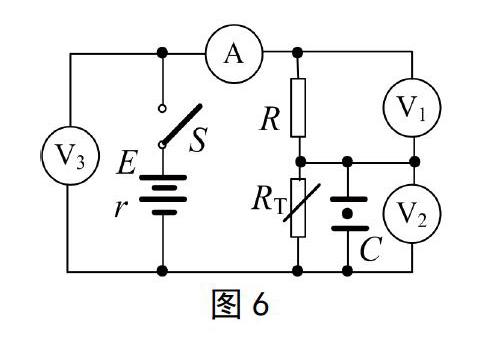
例4：（多选）如图6所示，E为电源的电动势，r为电源的内阻，R为定值电阻，RT为一热敏电阻，其阻值随温度的降低而增大。C是平行板电容器，当合上开关S，带电液滴恰能静止在C内。在热敏电阻温度降低的过程中，如果用ΔI、ΔU1、ΔU2和ΔU3分别表示电流表A，电压表V1、V2、V3示数变化量的绝对值，则关于该电路工作状态的变化，下列说法正确的是（  ）

A.RT不变时，电表V1、A示数之比等于R，电表V2、A示数之比等于RT

B.ΔU1/ΔI、ΔU2/ΔI、ΔU3/ΔI三者的比值均一定变大

C.ΔU1/ΔI与ΔU3/ΔI的比值保持不变，而ΔU2/ΔI的比值一定变大

D.C内的带电液滴将向上作加速运动

【解析】本题由重庆市2018届高三物理测试卷改编而来，不仅含有电学知识，而且含有力学知识，具有一定的难度，但重在考查动态电路的电压与电流的比值及二者改变量的比值变化，而如利用以上分析则能快速解答。

由图可见，电路呈明显串联关系，电流表A即测总电流I，电压表V1、V2、V3分别测R电压U1、RT电压U2和外电路中（R+RT）电压U3。热敏电阻RT值不变时，对各用电元件有U1/I=R1、U2/I=RT，表明各元件电压、电流之比值即为所测元件各自的电阻值，故A正确。

当温度降低，则热敏电阻值RT↑，根据题型一的“串反并同”判据，有U1↓、U2↑、U3↑、I↓。根据对ΔU/ΔI的分析，由于R为定值电阻，故有ΔU1/ΔI=R不变。ΔU2为所测可变热敏电阻RT电压改变量的绝对值，ΔU3为所测可变电阻（R+RT）电压改变量的绝对值。由以上分析可知，当ΔU为所测可变电阻的电压改变量时，其与通过可变电阻的电流改变量ΔI的比值ΔU/ΔI等于除所测电阻以外的其他元件的电阻值之和，于是有ΔU2/ΔI=（R+r）、ΔU3/ΔI=r，

可见均为恒值，故B、C错误。

RT不变时，C内带电液滴受向下的重力G和向上的电场力FE而处于平衡状态，即有G=FE=qE=q（U2/d）。现温度降低，应有RT↑→U2↑，于是电场力FE增大而G不變，结果带电液滴向上作加速运动，故D正确。

当动态电路中的电源存在内阻，要通过电路中电阻的改变来判断动态电路中U/I和ΔU/ΔI变化情形时，应根据电路的特性，利用欧姆定律将之等效于可变或定值电阻，并运用数形结合思想将之等效于函数图像的斜率来分析，如此能快速准确地解答此类题型。

3 结语

“串反并同”法和等效法是解决恒定电路动态变化问题的简单快速的有效方法，其中“串反并同”判据是最基础和应用最广的，等效法则运用数理结合、数形结合思想，能快速求解动态电路中的电压、电流比值及其变化量的比值变化问题。在动态电路的案例教学中或高考试题分析中，应探究其本质规律，由浅入深地设计这类逐级提升的题型来满足不同层次学生发展的需要，并渗透数理结合、数形结合思想来培养学生的物理学科素养和问题探究能力。

参考文献

[1]陈林芳，马如宝.动态电路中电压与电流的比值问题[J].物理教学，2013（5）：56-57.

[2]欧阳正杰.动态电路电学量的变化量比值解法的探讨[J].物理通报，2015（9）：51-52.

[3]孙德波，张知剑.滑动变阻器构成的动态电路模型及其应用[J].物理教学，2014（6）：18-20.

[4]赵勇功，突破“动态电路分析”的常用方法[J].中学物理教学参考，2015（4）：37-38.

[5]石雪山，动态电路问题分类解析[J].物理通报，2012（2）：

53-56.