求解小球在弹簧最低点加速度二法

◇ 甘肃 张永峰

求小球在弹簧最低点的加速度历来是高中物理的难点,用能量法和图象法妙解小球在弹簧最低点的加速度,强调科学思维的作用,体现了新课标要求的学科核心素养.本文从经典的模型开始,用能量法和图象法讨论小球在弹簧最低点的加速度.

图1

模型再现如图1 所示,轻弹簧下端固定在水平面上.一个小球从弹簧正上方某一高处由静止开始自由下落,接触弹簧后把弹簧压缩到一定程度后停止下落.在小球下落的这一过程中,下列说法正确的是( ).

A.小球刚接触弹簧瞬间速度最大

B.小球自接触弹簧起加速度方向变为竖直向上

C.从小球接触弹簧到到达最低点,小球的速度先增大后减小

D.小球在最低点时的加速度大于重力加速度g

分析小球刚接触弹簧时弹力F＜mg,加速度方向向下,与速度方向一致,随着压缩程度的不断增大,小球做加速度逐渐减小的加速运动;当F＞mg时,加速度方向向上,与速度方向相反,随着压缩量的不断增大,小球做加速度逐渐增大的减速运动,直到速度为0;当弹力F＝mg,小球加速度为0,速度最大,选项A、B错误、C正确.

小球在最低点时的弹力一定大于重力,但小球在最低点的加速度与g的关系和弹簧的弹力是否大于2mg有关,下面用两种方法加以分析.

能量法设小球从静止开始下落的位置距弹簧原长顶点的高度为h,小球到最低点时弹簧的压缩量为x.根据能量守恒,小球下落的全过程,重力势能全部转化为弹性势能,设弹簧的劲度系数为k,则有在最低点kx－mg＝ma,故有因h＞0,故一定有a＞g.

特例讨论,当h＝0时,即小球从弹簧原长处开始下落,代入.

图象法根据匀变速直线运动中,加速度随位移的变化图象与横轴所围面积表示速度平方之差的一半.

画出小球下落的加速度随弹簧压缩量(位移)的变化图象如图2所示,小球下落高度h时接触弹簧,速度为v0,小球压缩弹簧x1时,弹力F＝mg,小球加速度为0,速度最大为vmax;小球压缩弹簧最大xmax时,小球速度

为0,加速度为a.根据a-x图象和横轴所围面积表示速度平方之差的一半,因小球从接触弹簧到最大速度平方之差小于最大速度到弹簧压缩最大的速度平方之差的绝对值,故x＞2x1,又因为kx1＝mg,故根据kx－mg＝ma,可得a＞g.当h＝0时,小球接触弹簧初速度为0,压缩弹簧到最低点速度也为0,故此时x＝2x1,根据kx－mg＝ma,可得a＝g.

讨论小球在弹簧最低点时的加速度问题,关键是处理小球到最低点的位移问题.弹簧弹力是变力,用能量法和图象法讨论小球到最低点的位移,都巧妙解决了变力、变加速度求位移的问题,这是两种方法的巧妙之处.

模型应用如图3-甲所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.若以小球开始下落的位置为原点,沿竖直向下建立一坐标轴Ox,小球的速度v随时间t变化的图象如图3-乙所示.其中OA段为直线,AB段是与OA段相切于A点的曲线,BC段是平滑的曲线,则关于A、B、C三点对应的x坐标及加速度大小,说法正确的是( ).

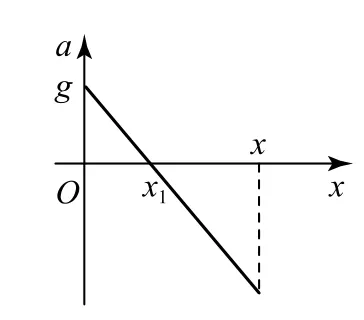
图2

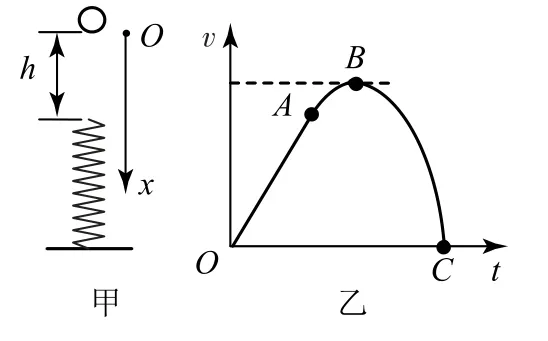
图3

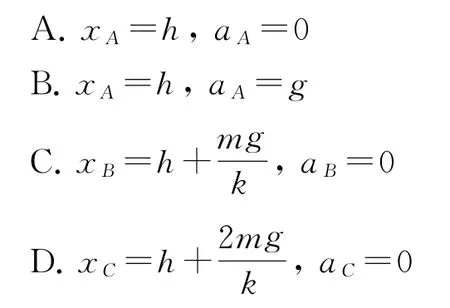
解析

在A点,xA＝h,弹簧弹力F＝0,故小球只受重力,a＝g,选项A 错误,选项B 正确;在B点,小球速度最大,弹力F＝kΔx＝mg,则xB＝h＋选项 C 正确;在C点,弹力大于重力,加速度不为0,选项D 错误.

本文用能量法和图象法巧妙地解决小球在弹簧最低点的加速度问题,得到弹簧的弹力,彰显了科学思维的作用,很好地体现了新课标要求的学科素养.