锤片式粉碎机主轴机构的多目标优化

徐伟，曹春平

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

锤片式粉碎机是重要的农产品加工装备，它有着构造简单、使用方便、粉碎效率较高等优点，因此在粮食及饲料等农业方面应用广泛[1]。主轴是锤片式粉碎机系统的关键机构之一。主轴上安装有转子，通过两个带座轴承固定，其作用是传递电动机所给的转矩，其性能的优劣将直接关系到粉碎机加工产品质量的好坏。锤片式粉碎机在工作时，利用电动机带动转子锤片高速转动来撞击物料，从而达到粉碎饲料的目的[2]。目前国内外对锤片式粉碎机的研究基本集中在粉碎室宽度、锤片末端到筛片的距离、转子直径以及吸风装置的设置等因素对锤片式粉碎机粉碎效率的影响，而对于粉碎机在结构方面的研究一直都很少[3]。鉴于此，以江苏某集团一经典型号的锤片式粉碎机为研究对象，通过分析转子的工作特性，利用ANSYS Workbench软件对主轴进行多目标分析，以转子上的主轴最大应力与最大应变为目标函数，对比3种不同的优化方案，确定一种最优方法来达到最佳的设计效果。

1 主轴的工作特性分析

本次研究粉碎机的电动机和主轴使用的是弹性套柱销联轴器直联传动，这种传动装置两个显著优点是传动轴没有侧向压力，传递功率可以很大。另一方面，由于本次研究的设备粉碎的对象主要是大米、小麦、大麦等小型颗粒物，在粉碎机工作时，锤片击打饲料时锤片的速度变化并不明显，因此对称的两排锤片因为速度差产生的离心力差很小，可以忽略不计。综上所述，转子上的主轴主要受如下几个力：安装在主轴上相对的两排锤片会存在质量差，所以两排锤片在绕着主轴转动时对主轴产生的离心力会有较大的差值，称为离心力差FN；安装在主轴上整个转子的重力G；电动机传递给主轴的转矩T。

下面具体分析这几个力：

1) 计算离心力差：按照某集团的锤片质量安装要求，径向相对称的两组锤片总质量相差不得超过2g，按照最大的质量差利用公式(1)进行计算：

(1)

式中：v表示锤片质心的速度；r表示质心到主轴轴心的距离。其中v=72m/s，r=232mm,所以F=44.69N。可以看出离心力差与转子自重和转矩相比很小，在进行受力分析可以忽略不计。

2) 计算重力：利用SolidWorks软件对锤片式粉碎机中的转子进行建模，定义材料属性之后，经过计算得出整个转子的重力为1 950N。全部加载到主轴的质心处即中心处。

3) 计算转矩：粉碎机的主要参数如表1所示，主轴受到的转矩利用公式(2)计算：

(2)

表1 粉碎机的主要参数

主轴的受力图如图1所示。

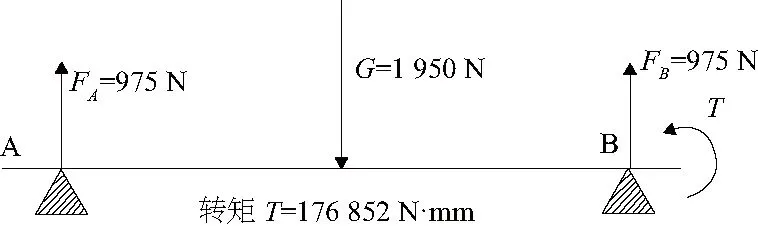
图1 主轴受力示意图

2 主轴的数值模拟与试验验证

锤片式粉碎机相比较于其他粉碎机，具有结构简单、生产效果较高、适应性较强等优点。对粉碎机粉碎效率的研究大多数采用试验的方式，这种方式成本高，比较耗时，而对于本次的研究目标来说可以通过数值模拟方式提高研究效率。首先建立简化的物理模型，进而根据物理模型建立有限元模型，进行有限元分析，最后进行主轴的应变测试试验来验证数值计算模型的可行性。

2.1 结构模型

利用Solidworks软件对主轴进行建模，为了使计算结果更加精准，有必要对主轴模型进行一些简化。合理的简化模型可以节约计算资源、缩短计算运行时间，提高分析效率，所以可以对主轴的圆孔、键槽等一些不需要的特征进行简化并删除[4]。图2是主轴的简化物理模型。

图2 主轴的结构模型

2.2 静力学分析

将建好的主轴物理模型导入到ANSYS Workbench软件中之后，对主轴进行网格划分。在进行计算之前，在软件中添加分析所要得到结果的模块，也就是主轴的应力和主轴的应变分析。根据上述的计算结果在主轴上插入载荷，由于主轴是与联轴器直接相连，因此将主轴与两端轴承座配合的两个面添加圆柱面约束，加载载荷时选择轴承载荷类型。计算结果如图3-图4所示。

图3 主轴的应力分析

图4 主轴的应变分析

为了对上述数值计算模型进行验证，对锤片式粉碎机进行主轴测量试验。由于上述数值模拟主轴的应力和应变是在同一加载条件和同一约束得到的模拟结果，所以对数值计算进行验证时只需要验证一方面即可。在这里验证最大应变要简单得多。因此选择对主轴进行应变测量试验。考虑到转子上主轴的受力特点以及多通道同步测量的要求，并满足桥路温度自补偿的要求，应变测量采用全桥电路。采用特制的应变片，将锤片式粉碎机的操作门打开，沿圆周方向90°间隔粘贴在主轴上进行试验[5]。连接线路图和现场测试图如图5、图6所示。

图5 全桥电路线路图

图6 现场测试图

2.3 验证结果

按照上述步骤完成测试，用应变仪来读出应变片的阻值变化，最后根据公式(3)计算：

(3)

其中：ε为应变值，K为灵敏度系数。测得主轴上应变最大值为ε=6.8×10-5，与数值模拟相差13.9%。因为在进行试验时是按照仿真数据来进行测试，在确定主轴最大应变位置处会有误差，因此测得数据会有一定的误差，但也在可允许的范围，数值模型可用于主轴的结构优化。

3 主轴优化模型的建立

3.1 优化计算的数学模型

本研究提出了3种优化方案，2种单目标函数优化方案和1种统一目标函数优化方案。

1) 方案1：以减小应力为目的，应尽可能减小主轴的最大应力σmax，目标函数就是：

minF1(X)=σmax

(4)

2) 方案2：与方案1相反，以减小应变为目的，应尽可能减小主轴的最大应变εmax，目标函数就是：

minF2(X)=εmax

(5)

3)方案3：根据平方和加权法思想，分别求出单个目标函数的最优值fi。由于各单个目标函数通常无法同时最优化，但在这里应尽量趋近理想点，所以，可构造出加权评价函数，将多目标问题转化为统一目标函数进行优化[6]，即：

(6)

通过公式(6)求出该式的最优解，便可得到原多目标函数的最佳值。W为加权因子，可以反映出各个目标在优化问题中的重要程度。由于应力应变对于主轴来说同等重要，因此可以取W=1。据此可构建本研究多目标优化问题的统一目标函数：

(7)

式中σmaxΔ以及εmaxΔ分别为最大应力与最大应变的最优值。

3.2 优化变量的确定

通过上述分析，开始对主轴的各个结构参数进行优化设计，但在优化过程中，因变量繁多，通常不会全部选择作为优化变量，只选择对目标函数比较敏感的设计变量进行优化[7]。主轴的各结构参数如图7所示：总共有L1-L6以及D1-D612个优化变量，其中D1=D5，D2=D4，L1=L5，L2=L4。

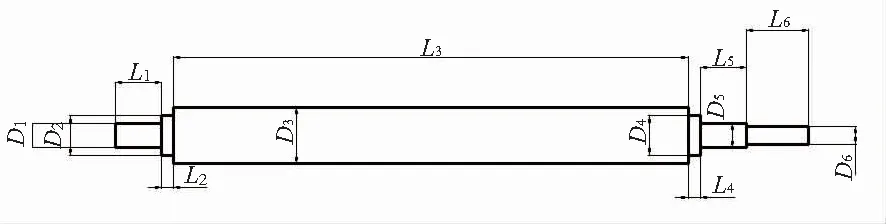
图7 主轴的优化变量

3.3 主轴结构灵敏度分析

利用ANSYS软件中的设计研究模块对各设计变量进行分析，计算上述优化变量对目标函数最大应力与最大应变的影响程度，如表2所示。

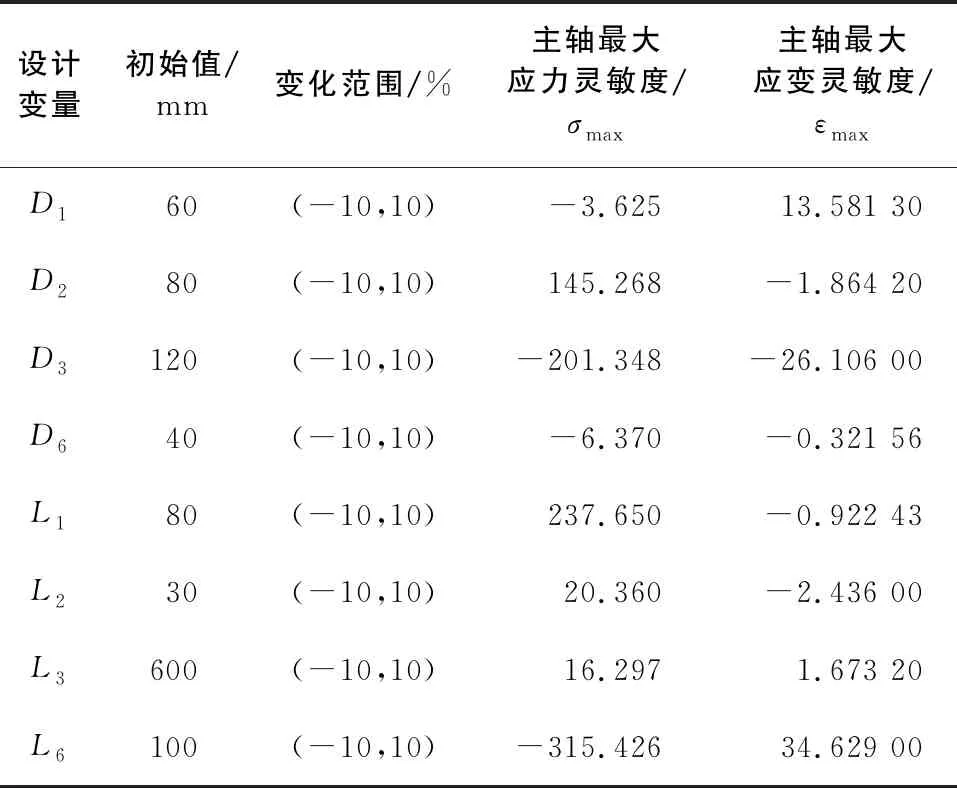
表2 灵敏度分析结果

分析表2可知，对主轴的最大应力灵敏度排序为

L6>L1>D3>D2>L2>L3>D6>D1，

其中L6、L1、D3、D2变量对主轴的最大应力的影响较大，并且D3、L6呈负相关性；对主轴的最大应变灵敏度排序为

L6>D3>D1>L2>D2>L3>L6>D6,

其中L6、D3、D1变量对主轴的最大应变的影响较大，并且D3呈负相关性。

综上所述，当采用方案1的时候，也就是使得主轴的最大应力最小，优化变量为：

X1=[L6，L1，D3，D1]T

当采用方案2的时候，也就是使得主轴的最大应变最小，优化变量为：

X2=[L6，D3，D1]T

当采用方案3的时候，需要综合考虑优化变量对主轴的最大应力与最大应变的影响程度，所以优化变量为[8]：

X3=X1∪X2=[L6，L1，D3，D2，D1]T。

4 主轴结构的优化结果

确定了3种方案的优化变量以后，利用ANSYS Workbench软件对上文3种方案进行优化，主轴优化方案经过16次迭代后收敛，最优结果序列为17。3种方案的收敛情况如图8-图11所示。

方案1

图8 主轴的应力优化收敛曲线

方案2

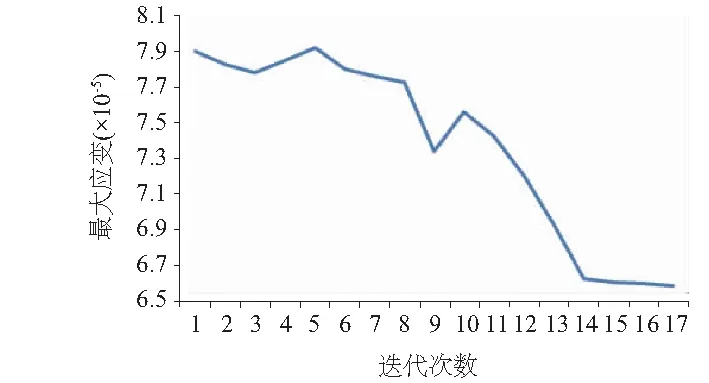
图9 主轴的应变优化收敛曲线

方案3

图10 主轴的应力优化收敛曲线

图11 主轴的应变优化收敛曲线

将3种方案优化之后整理的数据与初始数据进行对比分析，结果如表3所示。

表3 优化结果对照表

由表3可知，最大应力的初始值为15.383MPa，最大应变为7.90×10-5。对于方案1来说，经过优化以后最大应力为12.924MPa，下降了15.98%,但最大应变εmax却上升了9.7%；在方案2中，经过优化以后最大应变下降了16.7%,但是最大应力却上升了7.21%；在方案3中，经过优化之后最大应力下降了13.2%,并且最大应变同时也下降了13.5%。综上所述，对于方案1来说，虽然在降低最大应力这个单个目标上优化效果比较突出，但是同时也导致最大应变上升；在方案2中，也是存在这样的问题，因此这种只得到单个目标优化效果的，在通常情况下是不采纳的。对于方案3来说，对于主轴的最大应力和最大应变两个目标优化效果虽不及上述两种方案中单个目标的优化效果，但是都得到了不错的优化效果，对于这种多目标优化问题来说，这种方案无疑是最佳选择，因此，对于主轴的最大应力与最大应变优化方案选择优化方案3。

5 结语

1) 对某集团的锤片式粉碎机进行了研究，通过分析粉碎机主要结构转子的工作特性，并对主轴进行受力分析，得出了主轴在粉碎机工作时的受力模型，为运用软件对主轴进行静力学分析奠定基础。数值模拟结束之后提出用测试主轴最大应变的方法来验证其合理性。针对减小主轴的最大应力与最大应变问题提出3种优化方案，其中包括2种单目标优化方案和1种统一目标的优化方案，为数值模拟优化提供理论支撑。

2) 确定主轴的设计变量，运用ANSYS Workbench对设计变量进行仿真优化。

3) 在3种方案中，第3种即用平方和加权法思想建立的统一目标函数优化方案综合优化效果最佳，因此选择第3种方案为这次优化仿真的最终方案。优化后主轴的最大应力下降了13.2%,最大应变同时也下降了13.5%。