基于主成分分析与SVM的碳纤维复合材料损伤声发射信号模式识别
张璐莹,李 伟,姜智通,蒋 鹏,李彩瑞
(东北石油大学 机械科学与工程学院,黑龙江大庆 163318)
0 引言
碳纤维复合材料(Carbon Fiber Reinforced Polymer,CFRP)性能优良,抗冲击性好,质量轻,在能源加工、航空航天等领域应用广泛。但因其常在摩擦、撞击、疲劳等环境下工作,往往会出现较为复杂的损伤状态,且损伤状态的累积会导致设备的宏观失效,产生安全隐患[1]。因此,如何实现碳纤维复合材料损伤演化过程的准确表征和损伤模式的有效分类具有较强的现实意义和应用价值[2]。
材料内部诸如裂纹形成或扩展等局部源快速释放能量,并以瞬态弹性波的形式释放的过程称为声发射(AE)现象。声发射技术具有高灵敏度、频响范围宽,能实现动态监测等优点,在复合材料结构性损伤检测中具有良好的效果[2]。早在1997年,Surgeon等[3]对SiC复合材料进行了声发射监测下的拉伸试验;1999年,Morscher等[4]运用线定位的方法对SiC复合材料进行了拉伸试验,并利用Felicity效应对损伤状态进行评价,得到了复合材料损伤与弹性模量及声速的关系;2000年,杨盛良等[5]利用参数、波形分析了金属基、陶瓷基复合材料因为受力而产生变形损伤的声发射信号;2003年,刘怀喜等[6]对比了多种应用于复合材料损伤评价的无损检测方法,总结得到声发射技术在动态演化规律表征和损伤类型分类中具有较好的效果;2004年,王波等[7]通过试验获得了C/SiC复合材料的主要力学性能参数以及损伤过程变化规律;2008年,Marec等[8]对树脂基复合材料试件进行损伤模式识别,并结合聚类分析方法实现了不同损伤类型信号的有效区分;2013年,周伟等[9]研究了风电叶片内部损伤情况及包含预缺陷的风力叶片的力学性能;2014年,温泉等[10]通过划痕试验研究了复合材料毛刺及撕裂两种缺陷的产生原理;2015年,Maillet等[11]利用试验所得的声发射信号实现了对能量衰减的表征,并得到了能量衰减与声发射信号的关联;2017年,马云阔等[12]通过碳纤维复合材料层合板弯曲试验,并运用小波包特征熵的分析方法,对试件的不同类型损伤声发射信号实现了有效识别;2018年,Jalal等[13]结合Lamb波和模糊聚类两种方法,实现了复合材料不同损伤类型的识别。
从现阶段研究来看,大多研究者均选择声发射信号的参量分析作为损伤演化分析的基础,这一过程需构建大量的声发射参数样本,且易受到人为因素以及试验参量采集的影响,难以体现更为客观的损伤机理[14]。对于碳纤维复合材料损伤所具有的数据样本数量多、分布随机、变化形式较为离散等特点,现有模式识别方法在特征信号提取上有所不足。本文首先通过经验模态分解(EMD)实现碳纤维复合材料层合板弯曲试验所得声发射信号分解,然后进行特征频率提取、主成分分析及支持向量机的信号识别,进而确定试件损伤类型。如果能较为准确地识别碳纤维复合材料损伤类型,此方法可以实现更加准确、客观的碳纤维复合材料损伤类别研究。
1 主成分分析(PCA)及支持向量机(SVM)的处理方法
在利用时频分析方法进行碳纤维复合材料损伤分析过程中发现,大多数典型损伤类型声发射信号的时域特征并不明显,声发射信号的模式识别效果较差,因此,对于不同损伤类型信号常需要从频域特征入手,通常将原信号进行时频转换,进而获得损伤信号特征信息。本文从时频分析入手,建立EMD-PCA-SVM模型,以实现纤维断裂和基体开裂这两类损伤的有效识别。该模型由三部分组成:(1)AE信号经验模态分解;(2)特征频率集主成分分析降维;(3)利用SVM分类器实现复合材料层合板弯曲损伤识别分类。其模式识别流程如图1所示。
1.1 EMD方法
经验模态分解(Empirical Mode Decomposition,EMD)具有优于傅里叶时频变换效果的特点,常被用于非线性特征及非平稳性特征的信号分析领域。
EMD方法以原信号中各组分在时域上的特性实现分解。EMD方法可自发地将原信号处理成1组本征模态函数(IMF),所得到的本征模态函数即包含原信号特性,所有本征模态函数应具备以下两个特点:
(1)所有IMF具有的极值点及零点个数数值上不超过1;
(2)任意位置的局部极大、极小值点组成的上、下包络的均值为0。
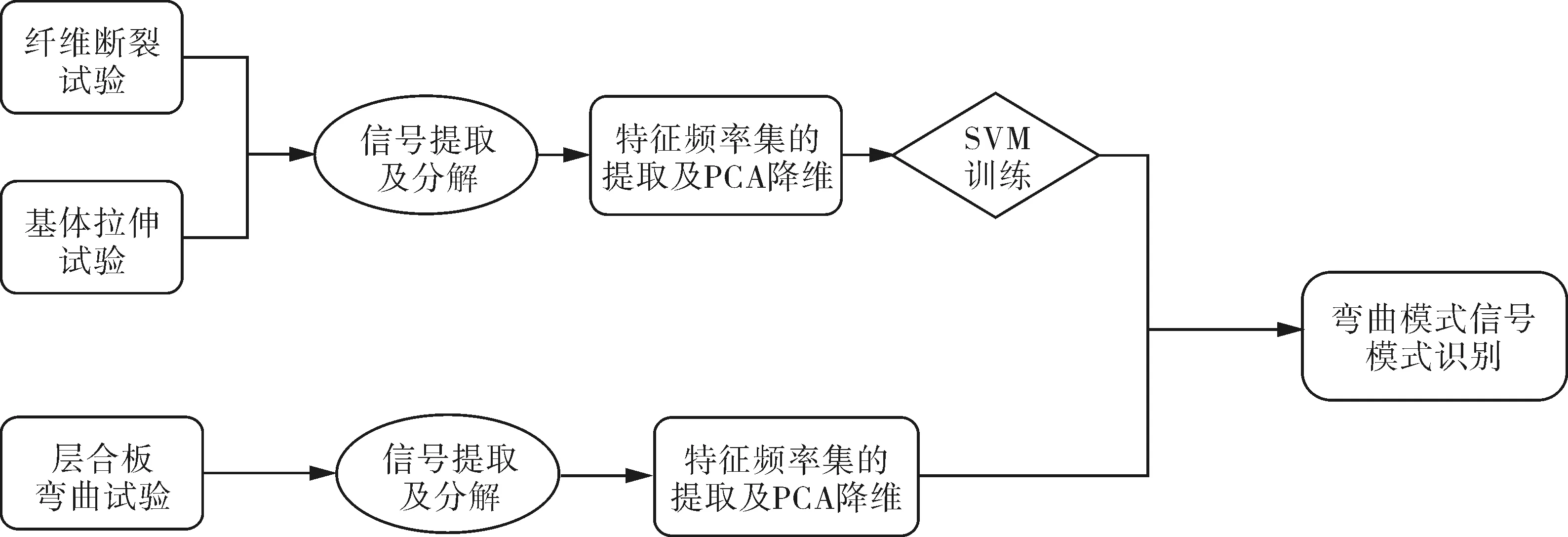
图1 模式识别流程示意
依据以上IMF须满足的要求,EMD核心过程如下。
(1)计算得出x(t)的极值,进而获得上下包络线。
(2)计算上下包络线所具有的平均值m1。
(3)用信号x(t)减去m1得到1个去掉低频的剩余部分h1(h1=x(t)-m1)。筛选的过程必须重复多次,以满足IMF的限制条件。筛选如下:
h1-m11=h11
(1)
k次迭代后:
h1(k-1)-m1k=h1k
(2)
当h1k满足条件后,即可获得c1:
c1=h1k
(3)
从x(t)提取c1后并进行分离:
x(t)-c1=r1
(4)
对r1重复上述的筛选,计算获取另一个新的IMF。该过程反复进行筛选,得到:
r2=r1-c2
(5)
rn=rn-1-cn
(6)
若rn是单调的或满足只存在唯一极值并且无法运算获得更多的固有模态分量时,结束运算过程,则分解所得最终结果为:
(7)
式中n——固有模态函数总个数;
cj——第j阶的固有模态函数;
rn——自适应趋势或者常数的残余量。
最终原信号被分解成多个固有模态分量以及一个残余量rn(rn表示一个自适应趋势或代表常数)。
1.2 主成分分析(PCA)
PCA方法的实质是将高维数据投影至低维子空间,进而提取其内在信息[15]。在主成分分析中,X被处理为两部分:载荷矩阵和分数矩阵。分解为:
(8)
其中,X∈Rn×m包含n个训练样本和m个测量样本;T∈Rn×A为得分矩阵;P∈Rm×A为载荷矩阵,A表示主要的成分数量;E表示剩余矩阵。选择CPV(累计方差百分比)方法确定A的值。模型内部定义两个监测指标SPE和HotellingT2,其中SPE为变量相关度,HotellingT2表示测量样品之间的距离和原点的主成分子空间[16]。SPE和HotellingT2计算公式如下:
SPE=‖(I-PPT)X‖
(9)
(10)
X=[X1,…,Xm]是一个实测样本。
1.3 支持向量机(SVM)
支持向量机(SVM)理论提出于1964年,其特点是利用监督学习的手段对数据二元分类,其实质是将学习样本所具有的的最大边距超平面作为决策边界[17-19]。其最优超平面分布见图2。
图2中两侧为两类差别迥异的样本,虚线H1,H2的距离代表分类间隔。可以实现分类间隔最大的分类线称作最优分类线[20-21]。xw+b=0即为分类线性方程,经归一化处理,样本集合(xi,yi)(其中,i=1,…,n,x∈Rd,y∈{+1,-1})满足:
yi[(wxi)+b]-1≥0,i=1,…,n
(11)
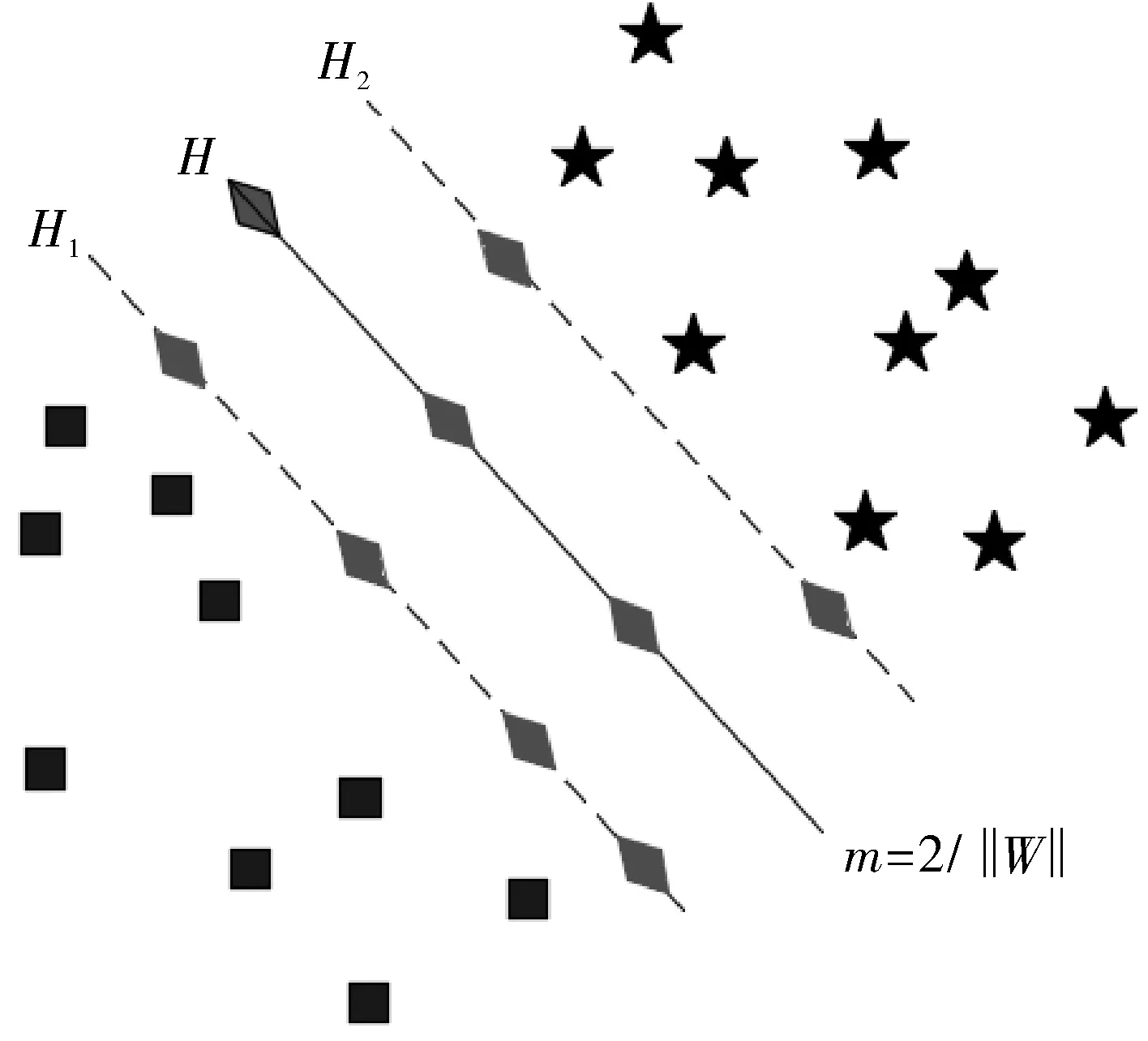
图2 最优超平面分布
SVM借助于非线性变换的手段,可将实际问题转换到高维空间,进而实现将其解决,其中K(xi,xj)≡φ(xi)Tφ(xj)被称为核函数。核函数通常有4种,具体如下。
(3)径向基函数(Radial basis function):K(xi,xj)=exp(-γ‖xi-xj‖2)(其中,γ>0表示间隔松弛向量)。
2 试验设备与方案
为了提高样本获取准确率,首先针对纤维断裂和基体开裂损伤设计单一损伤类型特征试验,其中纺锤体试件按照GB/T 1040.4—2006《塑料 拉伸性能的测定 第4部分:各向同性和正交各向异性纤维增强复合材料的试验条件》制备,纤维束试件由T700碳纤维束及铝片组成。面内弯曲试验试件为T700环氧树脂基碳纤维复合材料层合板,编制铺层方式为[45°/-45°]14。尺寸为200 mm×200 mm×2 mm(长×宽×高),采用铝制夹具固定。T700碳纤维束详细参数见表1。

表1 T700碳纤维束参数
试验设备主要包括Disp-16宽频声发射检测系统、STM原位微型拉伸系统和岛津万能拉伸试验机。其中声发射采集传感器选择两种型号:W/D型宽频带传感器及Nano型传感器。本次试验门槛值为35 dB,高于背景噪声9 dB,能够满足屏蔽背景噪声的要求。同时,利用PAC2/4/6前置放大器进行前置放大,放大增益为40 dB,具体系统配置参数如表2所示。

表2 声发射监测系统参数设置
碳纤维复合材料损伤试验共分为两类,一种为单一损伤模式声发射监测;另一种为碳纤维层合板面内弯曲声发射监测。两类试验采用同样的系统、传感器及参数设置方式,在正式试验前均对试件进行预拉伸与弯曲,主要为了消除夹具与试件之间的摩擦噪声。纺锤体以及纤维束试件连续拉伸过程中,以位移速度1 mm/min拉伸至试件彻底宏观失效。单一损伤试验装置如图3所示,面内弯曲实验装置如图4所示。面内弯曲试验以位移速度1.5 mm/min锤头下降对层合板进行弯曲加载,直至试件失效。
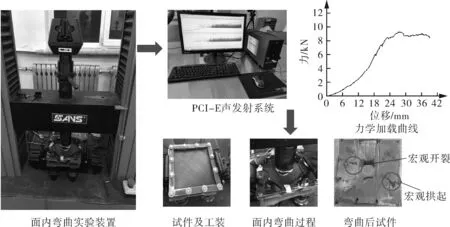
图4 面内弯曲实验装置及试件
3 试验结果
3.1 单一损伤类型声发射试验参量时域经历分析
图5~8分别为基体开裂、纤维束拉断振铃计数经历图和基体开裂、纤维束拉断参量关联图。
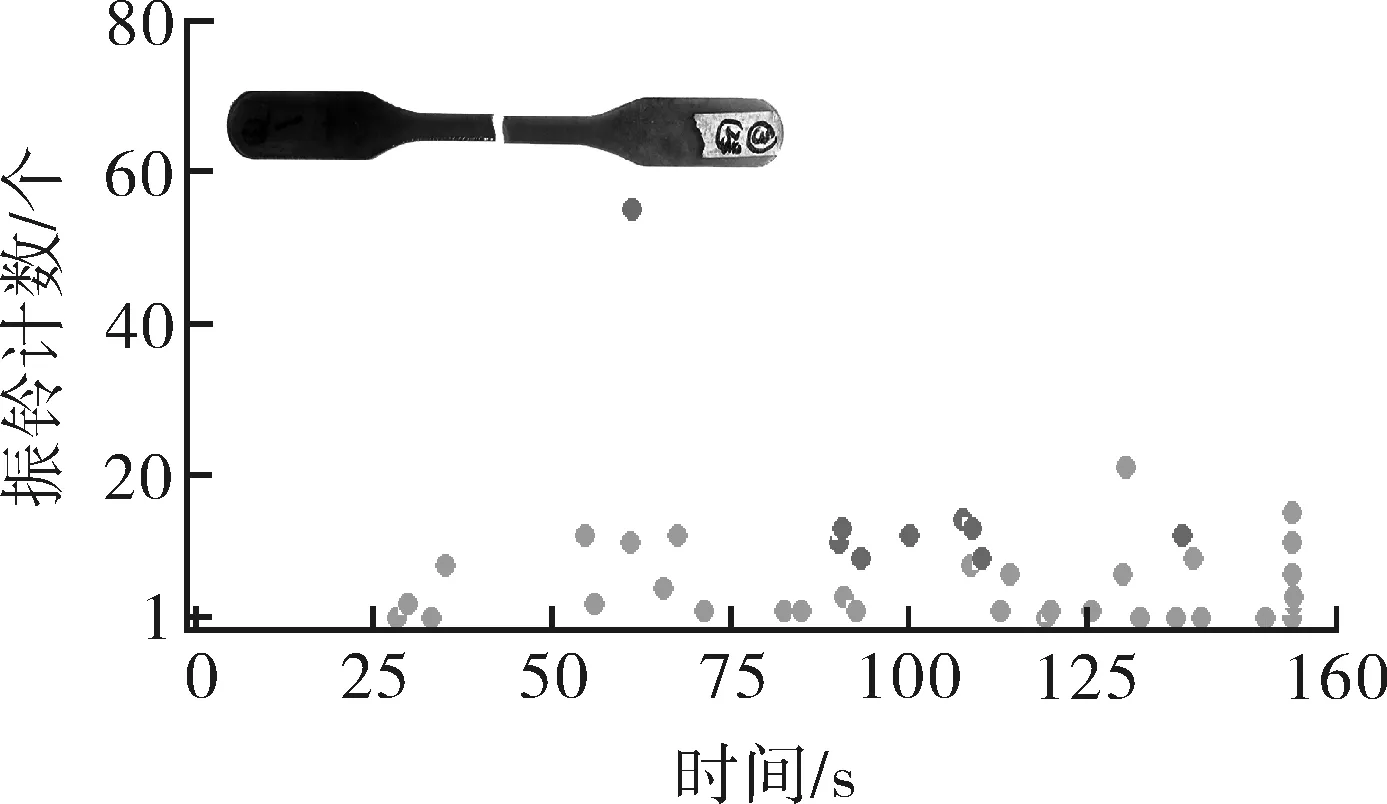
图5 基体开裂振铃计数经历图

图6 纤维束拉断振铃计数经历图
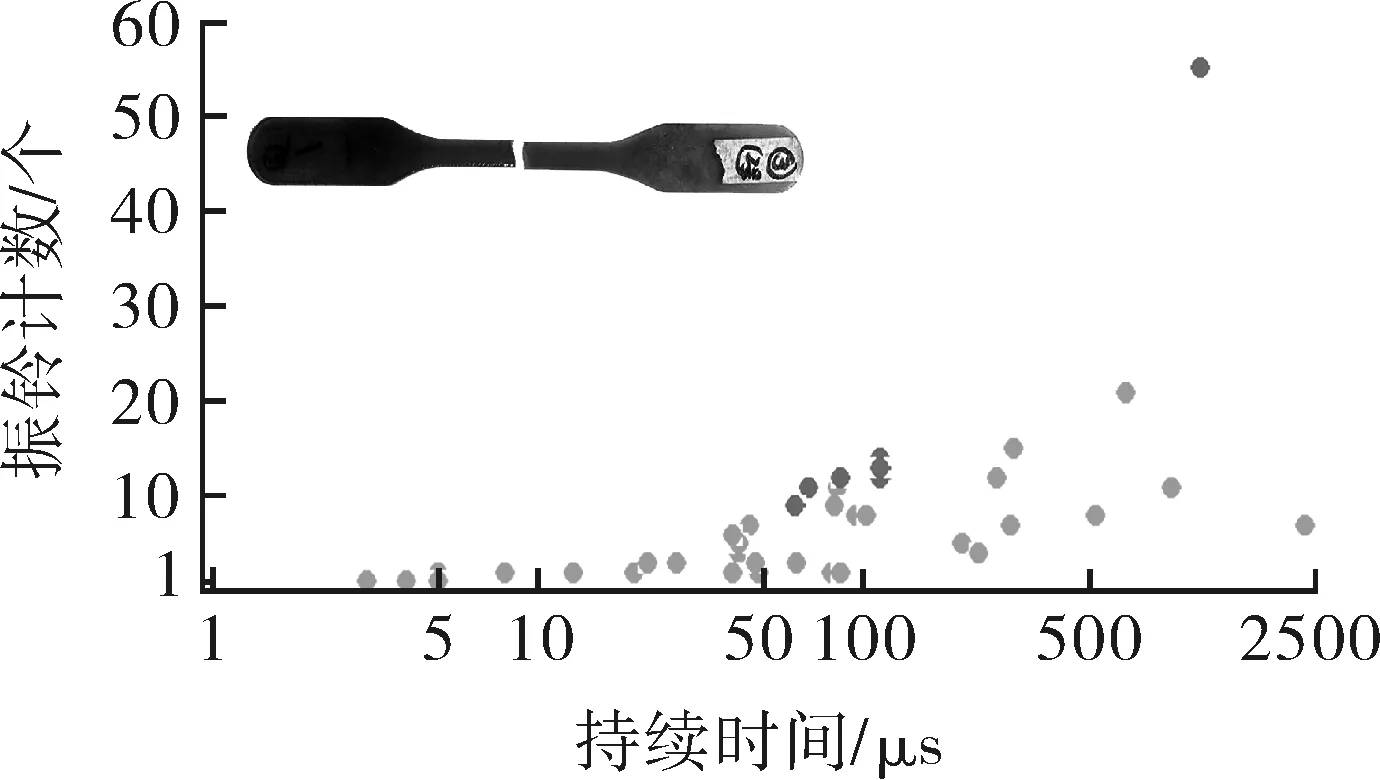
图7 基体开裂参量关联图
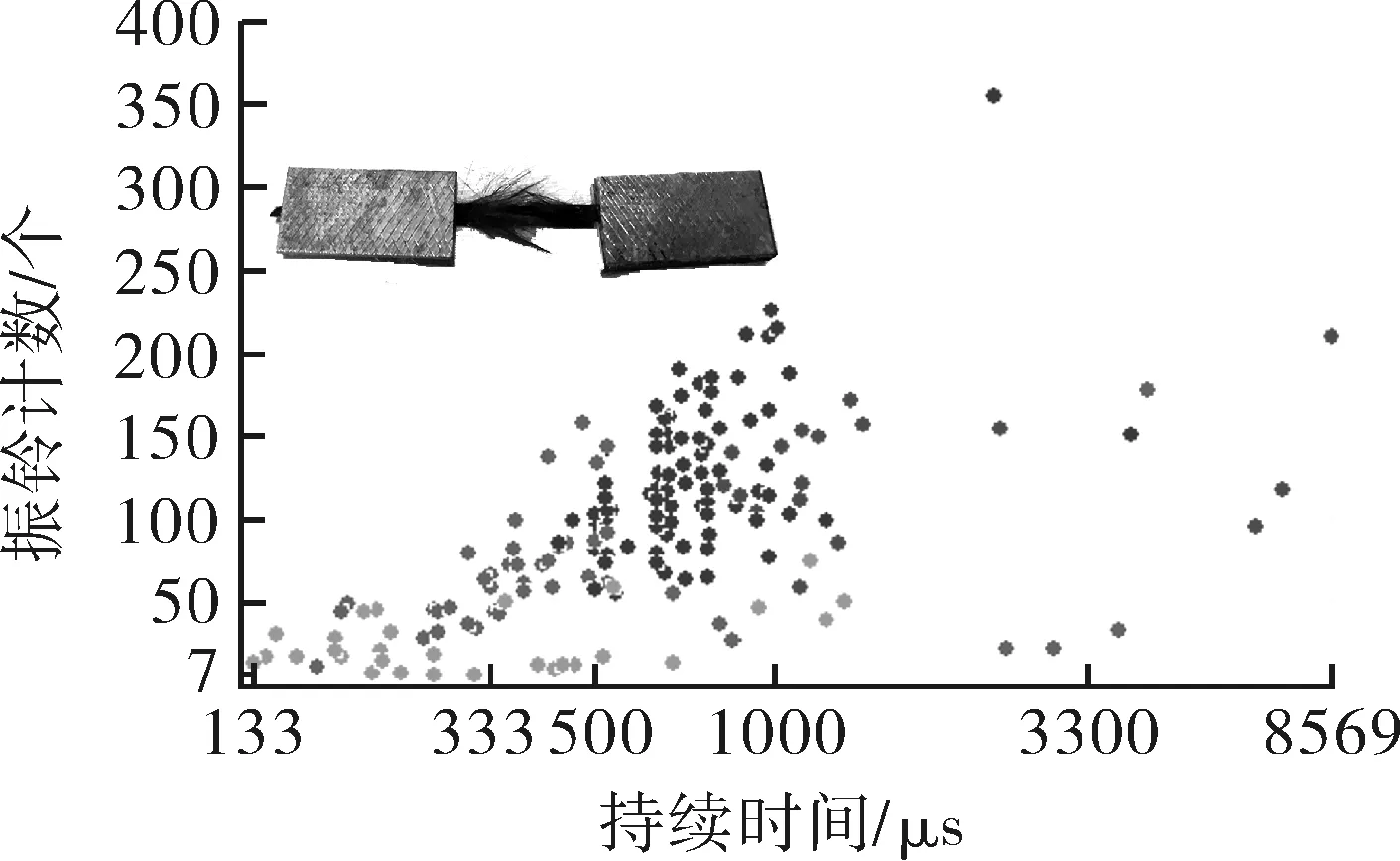
图8 纤维束拉断参量关联图
从图5~8可以看出,基体开裂过程声发射振铃计数(counts)和持续时间均处于较低水平,这说明整体信号强度较弱,幅值分布于40~76 dB,属于中低幅值信号;纤维束拉伸过程整体声源counts较小,主要分布于50~250左右,但幅值较高,大多数信号幅值高于70 dB,部分信号幅值达到90 dB。结合试验过程可以看出,由于拉伸前期很多碳纤维处于松弛、相互缠绕甚至弯曲的状态,伴随载荷分布必然存在逐渐绷紧的过程,在这个过程中纤维间发生相互摩擦,进而产生大量的低幅值、低能量声发射信号,且由于拉伸过程中是纤维束整体承受拉伸载荷,理想状态下应为同时断裂,但由于实际试验过程中难免出现少量作用力分布不均现象,因此会出现纤维束之间的相互摩擦以及个别纤维束断裂后的应力再分布,因此纤维拉伸过程中声源幅值在40~90 dB较宽范围内分布,而伴随载荷逐渐增大,高幅值、高能量的声发射信号开始大量的出现,故出现90 dB以上的声发射信号。这说明此阶段纤维已经开始连续发生断裂。同时伴随很多的低幅值声发射信号,这是因为即便是加载的末期,依然有强度较大的纤维处于弹性阶段,其弹性变形也会产生小幅值的信号。另外,这个阶段依然会少量存在着纤维的摩擦,也会产生低幅值信号。从参量分布范围可以发现,虽然基体开裂和纤维断裂信号参量特征有所不同,但是数值范围有部分重合,基本属于一个数量级,差异性较小,因此,单纯采用特征参量方法实现不同损伤信号识别有较大难度。
3.2 层合板弯曲声发射试验参量时域经历分析
试件弯曲过程采用压向四点弯曲形式,利用方框型夹具对正方形层合板试件施加约束。加载过程由圆柱形压头向下均匀施加载荷、直至试件失效。从图4中弯曲后试件图可以看出,从宏观看试件在试验过程中出现了明显的开裂和子层拱起现象,在开裂中包含了基体开裂及纤维断裂损伤两种类型,子层拱起则明显由分层损伤构成。
选择能量、振铃计数、幅值作为声发射特征参量进行参数经历分布分析,如图9所示。
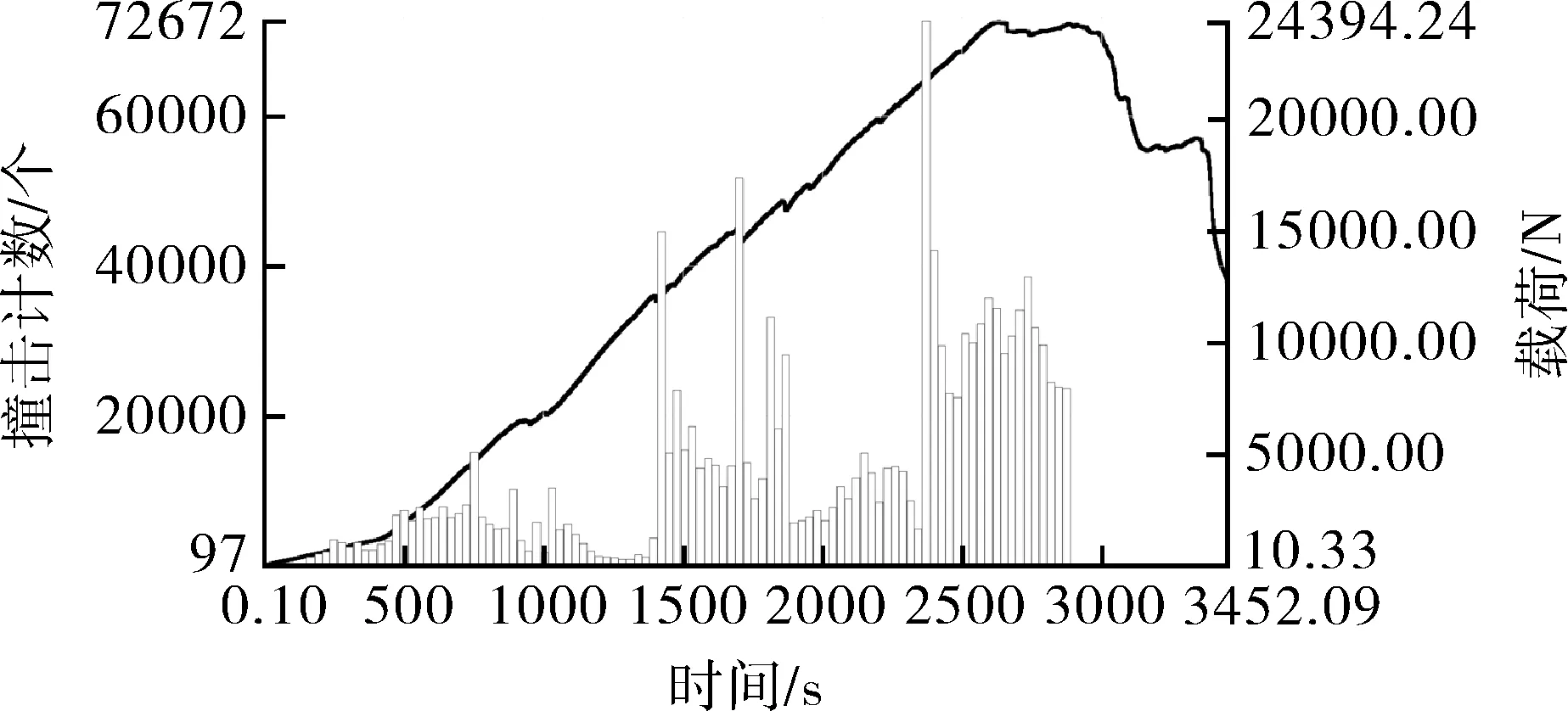
(a)时间-撞击计数-载荷
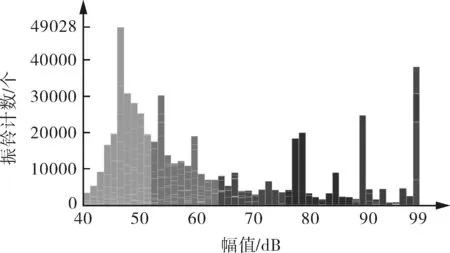
(b)幅值-振铃计数

(c)幅值-能量-振铃计数
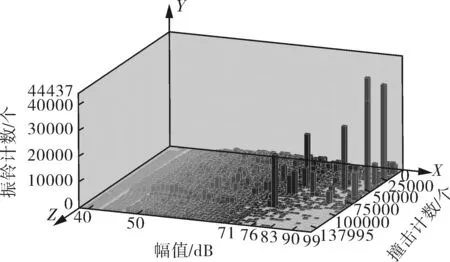
(d)幅值-撞击计数-振铃计数图9 面内弯曲声发射信号参量图
在图9(a)中,撞击计数的变化规律与载荷波动有较好的一致性,且在波动位置出现了撞击计数的明显增大,这说明载荷的波动对应试件局部的失效与载荷再分布状态。而从图9(b)中可以看出,从幅值分布角度分析,整个承载过程的损伤声发射信号大多由<70 dB的中低幅值信号构成,且低幅值信号部分出现振铃计数的峰值。由图9(c)可以看出,低幅值、低振铃计数信号分布较为均匀,高振铃计数信号呈现大能量与高幅值状态,且主要出现在试验后半程。由此可以看出面内弯曲损伤声发射信号特征具有低幅值、较大振铃计数的特点,此类信号声源机理为较低水平,且衰减速度较慢,通常对应基体开裂及分层损伤模式中。而另一种在试件接近失效时出现部分高幅值,从幅值角度分析,高能量信号、大振铃计数信号与纤维断裂信号高度相关,其来源于层合板承载过程中出现的基体开裂扩展后造成的纤维断裂。通过以上分析可以发现,通过参量分析大致能够发现层合板弯曲过程声发射信号出现两类信号特征分布,但不能较好地表征损伤类型,可以通过模式识别方法对这两类信号进行特征提取与分类。
4 试验结果分析
4.1 特征频率提取
分别在纺锤体和纤维束拉断试验中提取基体开裂信号及纤维断裂信号样本各15个,从层合板弯曲损伤声发射信号中均匀提取40~100 dB幅值范围内的30个信号。对该60个声发射信号样本首先进行EMD处理,并计算分解后各IMF与原信号的相关度。提取相关度≥5%的IMF。以一个纤维断裂信号为例,图10为纤维断裂信号EMD图。其中IMF1~IMF10为由高频到低频的固有模态分量。
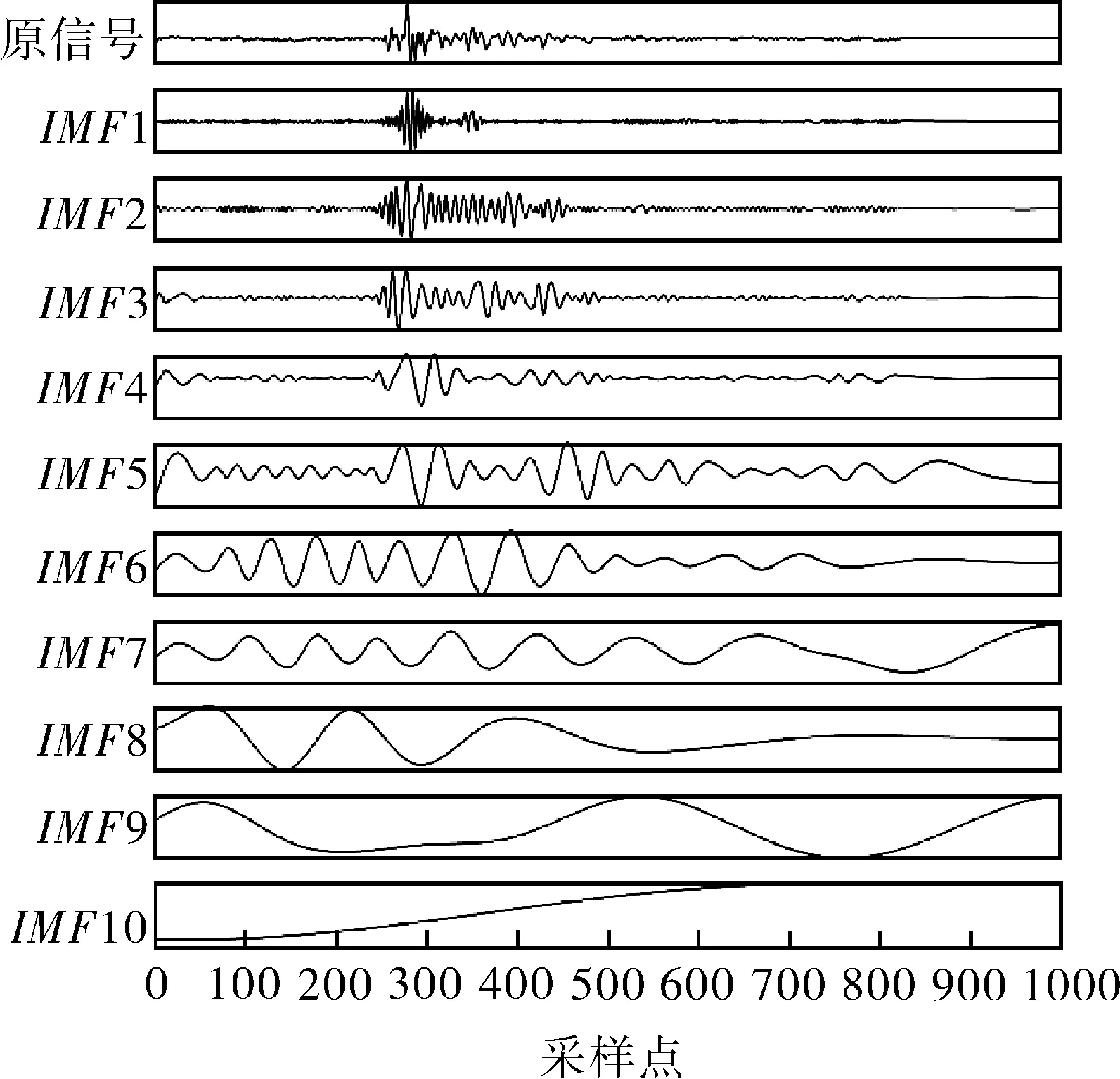
图10 信号EMD图
图11为各个IMF与原始信号之间的相关系数图。

图11 IMF相关系数图
选择相关度≥5%作为判据进行IMF分量优选时可以看出,IMF6,IMF7,IMF8,IMF9,IMF10分量不满足要求,将其余5个IMF分量作为有效的IMF。对这5个IMF分量进行快速傅里叶变换(FFT),可以看出其频率成分及分布具有明显区别,其波形及频谱图如图12所示。

(a)原信号图
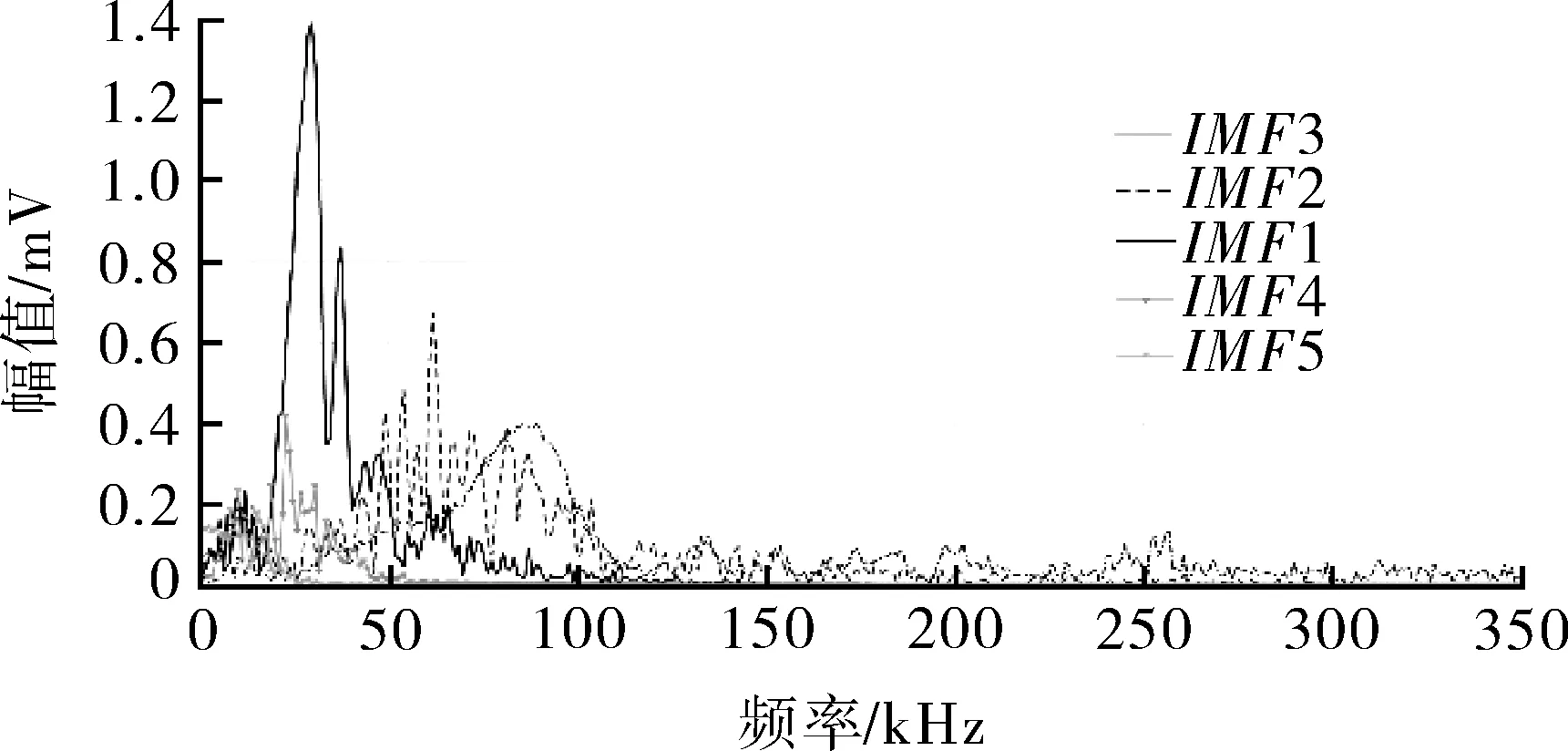
(b)FFT图谱图12 特征信号波形及频谱
变换后提取0~0.5 MHz范围出现的幅值较大的特征峰处频率值,得到了5个有效IMF的40个特征峰处频率值,组成一组40维的特征频率集。表3列出了15个纤维断裂信号、15个基体开裂信号及30个未知信号的特征频率集。

表3 样本特征频率集
4.2 主成分分析(PCA)与SVM分类
利用主成分分析法(PCA)实现对特征频率集的降维,降维结果见图13,纤维断裂及基体开裂信号经过分解并降维处理后的累计方差贡献率均在84%以上。原为40维的特征频率信号,经过PCA处理后得到2维度的降维信号,其累计方差贡献率为84.2%,即此2个主成分分量包含了原信息84%以上的信息量。
对60个AE信号以相同流程进行EMD、PCA降维处理,进而利用支持向量机识别器对纤维断裂及基体开裂两类损伤类型信号进行分类。诊断结果如图14所示。
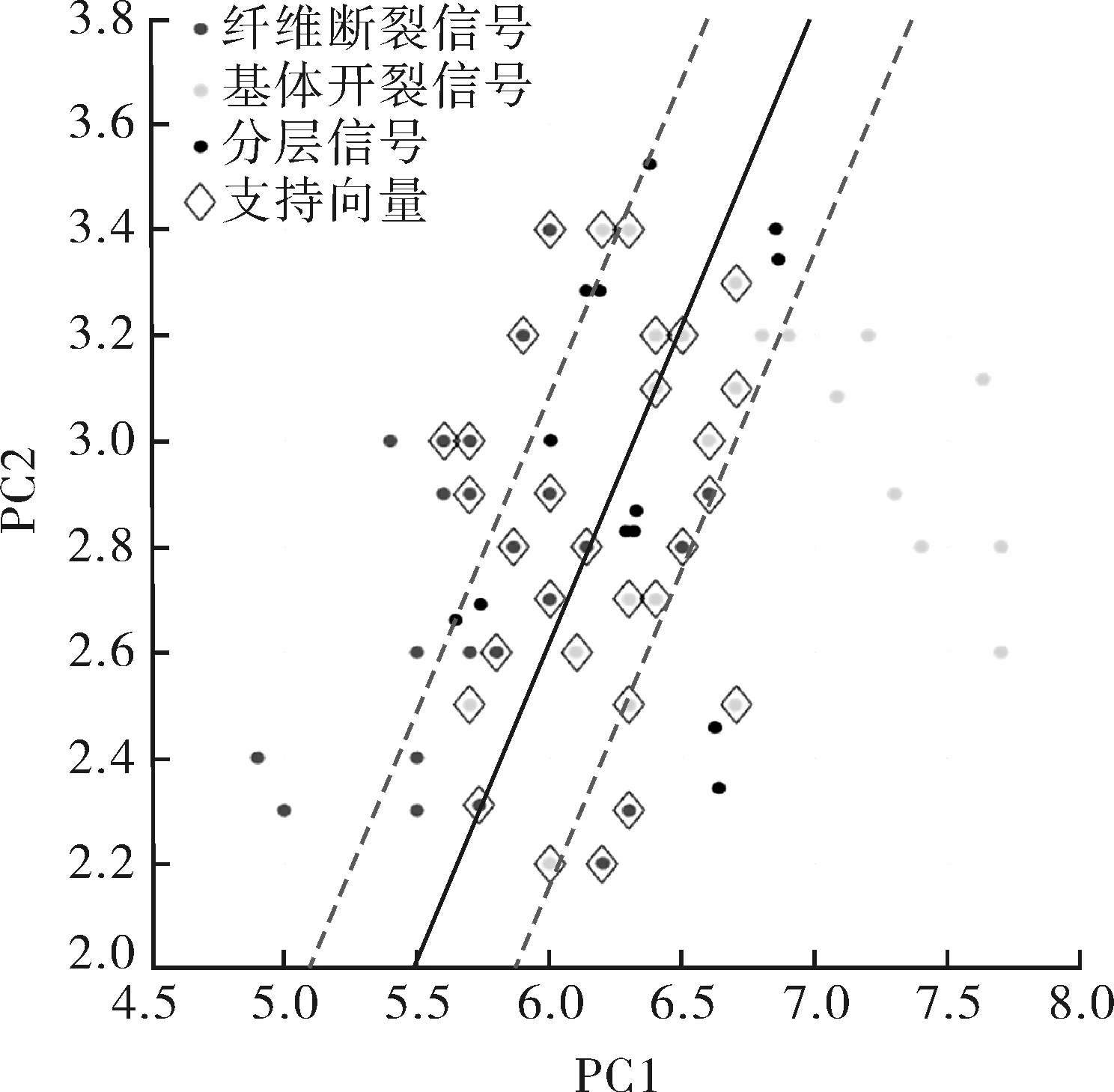
图14 SVM分类识别结果示意
从图14中可以看出,所建立的支持向量机识别器可有效地将纤维断裂及基体开裂两类信号进行分类。识别器的支持向量可将信号分为两类,图中两条虚线中间的区域为支持向量所在区,支持向量区域左侧为纤维断裂信号,支持向量右侧为基体开裂信号。在基体开裂及纤维断裂识别区域各选取一个信号,将基体开裂识别区和纤维断裂区所取信号编号为a和b,分别对所选择的这两个信号进行快速傅里叶变换处理,得到各自的频谱如图15所示。其中信号a的频率主要集中在20~100 kHz,最高幅值所在频率为67 kHz,与基体开裂信号特征相符。而信号b的频率主要集中在100~180 kHz,其中最高幅值频率105 kHz,与纤维断裂高频特性相符。由此可见,所建立的支持向量识别器的识别结果有较好的准确性。
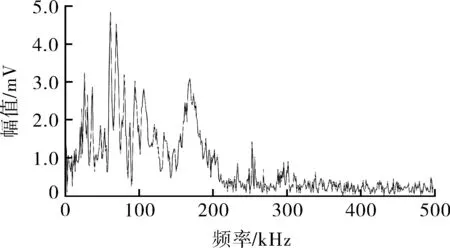
(a)信号a频谱图
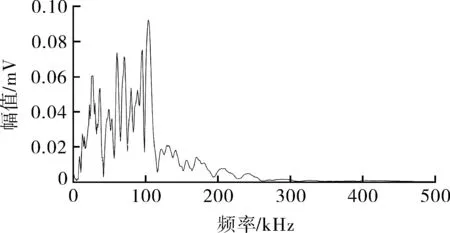
(b)信号b频谱图图15 分类后两类信号频谱图
利用SVM的交叉检验算法,选取15个纤维断裂试验所得信号、15个基体开裂试验所得信号、8个弯曲试验识别所得纤维断裂信号以及9个弯曲试验所得基体开裂信号共计47个信号,进行分解、特征频率提取及降维操作,从47个降维后信号中随机选择27个样本作为训练集,余下20个样本作为测试集,进行50次识别运算,其结果如图16所示。20个样本的平均识别率为83.1%,其中对纤维断裂失效形式的识别率为81.0%,对基体开裂失效形式的识别率为85.1%,绝大部分测试样本的测试结果与实际相符。可见,构建的分类器可对纤维断裂及基体开裂声发射信号进行有效地分类识别。

图16 识别率图
5 结论
本文针对碳纤维复合材料损伤声发射信号分类与提取问题,提出一种新的复合材料层合板损伤模式识别的方法,综合运用了经验模态分解(EMD)、主成分分析(PCA)以及支持向量机(SVM)等多种模式识别方法。通过典型损伤试验及数据处理研究得出以下结论。
(1)EMD-PCA-SVM模型可实现对纤维断裂及基体开裂两种失效形式进行预测分类。
(2)针对T700型碳纤维复合材料层合板弯曲试验过程所产生的基体开裂及纤维断裂缺陷特性信息,EMD-PCA-SVM模型具有较好的识别效果,可为后续碳纤维复合材料损伤及失效研究提供更为客观、准确的方法。
由此可见,以PCA和SVM相结合的声发射信号模式识别方法能够有效地实现碳纤维复合材料两类典型损伤信号的特征分类与提取,该方法在树脂基纤维增强复合材料的损伤机理研究及在役设备损伤监测方面具有广阔的应用前景。

