一种用于人致楼盖振动测试的光纤加速度传感器

金 峤，吴翔宇，王传克，孙 丽，朱春阳

(沈阳建筑大学土木工程学院，辽宁沈阳 110168)

0 引言

随着建筑及施工技术水平的提高、新型结构体系的采用以及轻质高强材料的使用，现代建筑逐渐朝着结构轻巧、造型独特等方向发展。其因质量、刚度的降低以及跨度的增大，使结构的楼盖体系拥有较低的竖向自振频率。若结构内部人员活动(如步行和有氧运动等)产生的谐振频率与楼盖自振频率相接近，就容易引发楼盖的振动。这种振动一般不会给结构带来安全性问题，但能给结构内部活动人员(振动的接收者)带来情绪上或心理上的不满或不舒适，影响人们正常生活[1-6]。

一般地，人致楼盖振动的频率范围为0～20 Hz，而人体对楼盖振动的敏感频率范围为3～10 Hz[7]。因此，用于人致楼盖振动测试的传感器工作频率范围应满足上述条件。相比较于传统的电类传感器，光纤光栅传感器由于采用光作为传递信号的载体，灵敏度要远远大于用电作为信号载体的电类传感器。在建筑结构的损伤、应力应变，甚至是温度监测上，光纤光栅传感器的高灵敏度都占据着巨大的优势。

基于人致楼盖振动的频率范围和光纤光栅传感器的优势，本文设计了一种量程及灵敏度可调的光纤光栅加速度传感器。首先，基于等强度梁的力学性能对传感器的整体结构进行了设计；其次，确定了适合该传感器的温度补偿方案；最后，设计了小振动台实验，对该传感器的幅频特性、灵敏度和横向抗干扰能力进行了测试。

1 传感器研制

1.1 传感器的整体结构设计

该光纤光栅加速度传感器主体结构主要由强度梁、L型转轴、圆形钢片、质量块和不锈钢外壳组成，其结构示意图和实物图分别如图1、图2所示。金属外壳起到固定等强度梁的作用，光纤光栅粘贴在等强度梁表面，圆形钢片焊接在L型转轴上，起着传导力矩的作用。

图1 传感器立体示意图

图2 传感器实物图

等强度悬臂梁采用60SiMn弹簧钢，其参数为：弹性模量为200 GPa，梁长度为60 mm，固定端宽度为16 mm，厚度为1 mm。

质量块采用铜作为材料，并将质量块加工成球形，其密度为8.9×103kg/m3，质量为69 g，理论自振频率为30 Hz。

底座、L型转轴和圆形钢片采用不锈钢材料制作。其中底座由底板和竖板组成，底板尺寸：长为100 mm，宽为80 mm，厚为2 mm。竖板尺寸：长80 mm，宽60 mm，厚5 mm。

L型转轴尺寸：两端分别为55 mm和85 mm。采用直径3 mm的光圆不锈钢筋制成。

圆形钢片尺寸：半径为15 mm，厚为2 mm。

光纤光栅中心波长为1 555.812 0 nm。

1.2 等强度梁的力学性能

在弯矩较大处采用较大的截面，在弯矩较小处采用较小的截面。这种截面沿轴线变化的梁，称为变截面梁[8]。等强度梁是一种特殊的变截面梁(如图3所示)其各横截面上的最大正应力都相等。

图3 等强度梁示意图

根据力学原理,在梁的任意表面上有：

W(x)=B(x)h2/6

(1)

(2)

即

(3)

式中：W(x)为X截面的弯曲截面系数值，mm3；B(x)为x截面处的宽度，mm；h为等强度梁厚度，mm；σ为正应力,MPa；M(x)为X截面的弯矩,N·mm；p为梁顶端所受的力，N；L0为等强度梁的长度，mm；x为X截面到固定端的距离，mm。

由上式可知，在p、h为定值的情况下，若要σ保持不变，则B(x)/(L0-x)也应为定值，即等强度梁的梁宽应随断面位置(L0-x)按线性关系变化。

B(x)=(L0-x)B/L0

(4)

此时等强度梁上下表面各点的轴向应变ε大小相同，均匀分布。

ε=6pL0/(EBh2)

(5)

式中：ε为等强度梁上下表面各点的轴向应变；E为弹性模量，MPa；B为固定端宽度，mm。

1.3 传感器工作原理

当该传感器受到来自地面的竖向振动激励时，等强度梁、钢片、转轴和质量块构成一个弹簧-质量系统，质量块以转轴为中心做轻微振动，钢片带动钢轴使等强度梁产生弯曲，裸光栅粘贴在等强度梁的受拉侧，与等强度梁协同变形，使得光栅的中心波长由于应变而产生偏移，再通过解调读出与加速度相对应的波长值。由于等强度梁是线弹性元件，所以理论上加速度与波长增量是成线性关系的[9]。

设质量块到转轴的距离为R，圆形钢片的半径为r，等强度梁的厚度为h，由力矩平衡原理可得：圆形钢片作用到等强度梁上的力为

式中：m为质量块的质量，kg；ag为外壳随支座运动在X坐标系中的加速度，m/s2。

光纤光栅加速度传感器可以简化为由振动质量块m、等强度悬臂梁的等效弹簧刚度k和阻尼c组成的二阶单自由度受迫振动系统[10]，如图4所示。X为空间固定坐标，Y为外壳的随体坐标，当结构随支座处于振动状态时质量块与外壳产生y的相对位移。

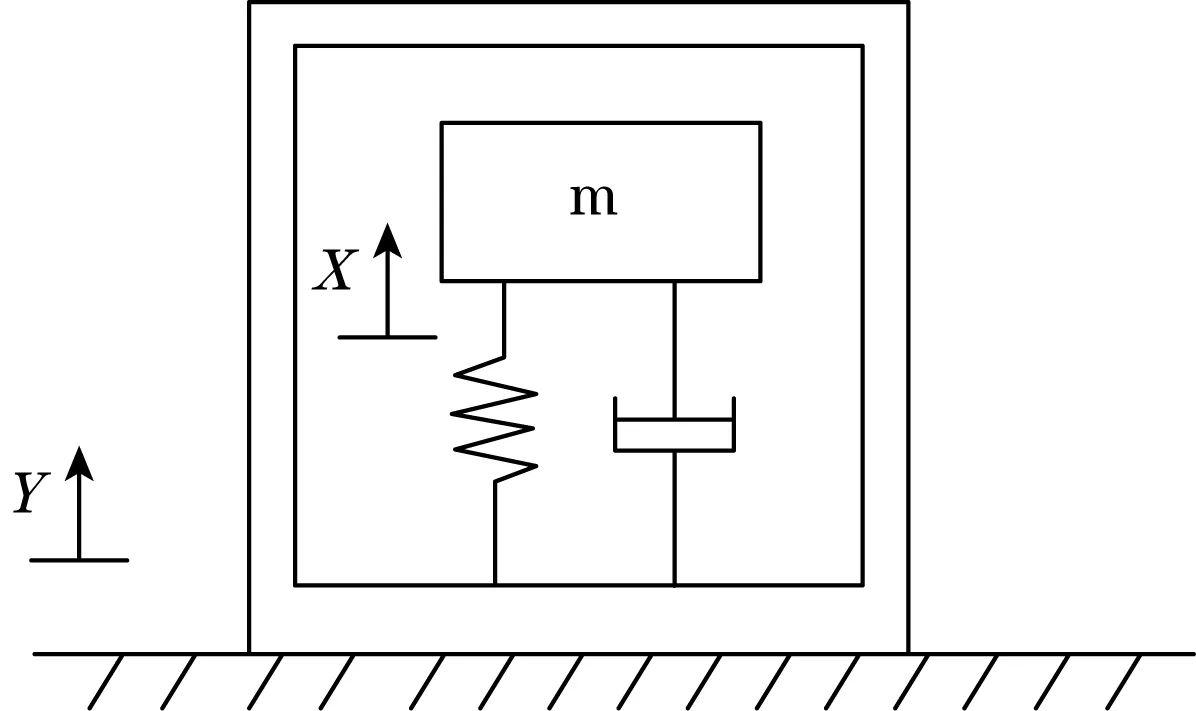
图4 二阶单自由度振动系统示意图

在Y坐标系中，质量块的运动方程为

(6)

式中-mag为Y坐标系的惯性力。

上式两边同时除以m可以得到：

(7)

(8)

(9)

式中：ζ为阻尼比；cc为临界阻尼，N·s/m；ω0为悬臂梁-质量块系统的固有频率，Hz。

(10)

加速度与波长的关系为

(11)

式中：Pe为光纤的有效弹光系数；λB为光纤光栅中心波长，nm。

从式(11)可见，加速度与波长的变化成线性关系。

设α=R/r为调节系数，当质量块滑动到轴上不同位置时，调节系数不断变化。钢轴上设置3个档位，见图5，3个档位的位置距离转轴的距离分别为R1=3r、R2=2r和R3=r。

图5 传感器档位示意图

当质量块处在第一档位时，调节系数α=3；当质量块分别固定到第二、第三档位时，调节系数α分别为2和1。从传感器的灵敏度公式可以看出，当质量块位于第一档位时，灵敏度最高。用字母I表示传感器的量程，由于光纤光栅的最大波长变化量是一定的，最大波长变化量与传感器的量程、灵敏度有着以下关系：

ΔλBmax=Smax·Imax

(12)

从式(12)可知，当传感器的波长变化量一定时，传感器的量程和灵敏度是成反比的[11]。在传感器追求高灵敏度的同时，需要降低其量程，反之亦然。

1.4 传感器的温度补偿方案

光纤光栅容易受到温度变化的影响，当环境温度变化1 ℃时，光纤光栅会产生大概10个微应变。在传感器的测量过程中，如果温度变化过大会使光纤光栅的波长产生漂移，严重影响测量精度。所以有必要对传感器进行温度补偿[12]。

传感器的温度补偿方法主要包括2种，即单光纤光栅补偿法和双光纤光栅补偿法。单光纤光栅补偿法主要从光纤光栅本身的结构和材料两个角度入手，主要方式包括：在光纤光栅外部设计一种新结构，利用新结构的材料属性和几何关系消除温度变化对光栅的影响；将负热膨胀材料应用到光纤光栅上，将其与光栅封装在一起。当温度变化时，负热膨胀材料与光纤光栅的温度膨胀特性正好相反，从而相互抵消，达到消除温度影响的目的。

与单光纤光栅补偿法相比，双光纤光栅补偿法则发展更为成熟，种类更多，目前主要包括：在传感器中的悬臂梁的两个表面均粘贴光纤光栅，二者均作为传感元件。二者处于同一温度下受温度影响发生的应变也相同，将二者的中心波长作差便可消除温度的影响；在传感器的监测位置布置另外一根光纤光栅，一个作为传感元件，一个作为温度补偿。作为温度补偿的光纤光栅的中心波长变化量就是温度的影响。

考虑上述两种方法，单光纤光栅补偿法对技术要求高，造价过高，而且新结构的稳定性能不高。除此之外，此方法对光纤光栅解调仪要求也较高，在悬臂梁上下表面粘贴光纤光栅，需要保证两个光栅处在悬臂梁的同一中心线上，否则会出现较大误差，制作难度较大。综合考虑，研制的传感器采用在传感器外部布置一根不受力光纤光栅，将其作为温度补偿。

2 传感器性能实验

2.1 实验仪器

本实验采用的仪器系统分别由小振动台(型号WS-Z30，见图6)、光纤光栅解调仪(型号iFBG-eDAQ-S15，见图7)和计算机连接构成。小振动台由WS-ICP-8 ICP压电加速度传感器、WS-5921/U60216-DA1型振动台控制和信号采集仪、WS-2401电荷放大器和功率放大器(GF-100B瓦功率放大器)组成。振动台控制和信号采集仪可以选择正弦波、地震波、白噪声和拍波等波形控制方式，波形经过D/A数模转换后再输入到功率放大器，从而控制振动输入。

图6 WS-Z30型振动台

图7 iFBG-eDAQ-S15型解调仪

将计算机和光纤光栅解调仪连接，并将光纤光栅加速度传感器连接到解调仪的一个通道上。同时，将光纤光栅加速度传感器固定到振动台上，使拾振方向与小振动台振动方向一致。

2.2 光纤解调仪采集频率的确定

本次实验使用的光纤光栅解调仪的采集频率范围为0～500 Hz，为了选择合适的采集频率，在性能实验前进行解调仪的采集准备。将其采集频率依次调整为100、200、300 Hz，将振动台的振动频率和加速度分别设置为20 Hz和1 m/s2开始测试实验。检查采集的数据发现：当解调仪的采集频率为100、200 Hz时，数据中出现了少量的空白点。当采集频率为300 Hz时，空白又多了一些。分析发生此现象的原因：传感器以20 Hz的频率振动，当解调仪的采集频率比较低时，对光纤信号的有效捕捉就差一些，当采集频率比较大时，采集到光纤信号没有变化就会出现空白。

振动台系统的信号采集仪要求采集频率要尽可能大于正弦波信号的频率，建议如果条件允许最好在10倍以上，目的是尽可能减少正弦波信号波形的失真度。

由于光栅作为传感元件灵敏度极高，为了避免漏采数据提高实验精确度，本次实验将光纤采集频率设置为最大值500 Hz，将振动台系统的信号采集也设置为500 Hz。

2.3 振动台时域输出与传感器响应

因为传感器的响应与振动台的时域响应与幅频特性无关，所以在验证这一特性时只将该传感器的质量块调至第一档位，将所有设备调试好后，通过振动台控制软件Vib’SQK(见图8)将振动台的振动频率调整为20 Hz，输出波形为正弦波，且振动台的输出加速度设定为1.5 m/s2。

图8 振动台控制软件

光纤光栅加速度传感器的时域响应曲线如图9所示。从图9可以看出：整体上曲线光滑度良好，对振动台的振动输出有良好的响应。

2.4 传感器的幅频特性实验

将振动台输出设计为正弦波，频率范围为1～30 Hz，振动台的输出加速度设定为1.5 m/s2。研究传感器在3个档位下的幅频特性，根据得到的数据绘制的3个档位下的实验结果见图10～图12。

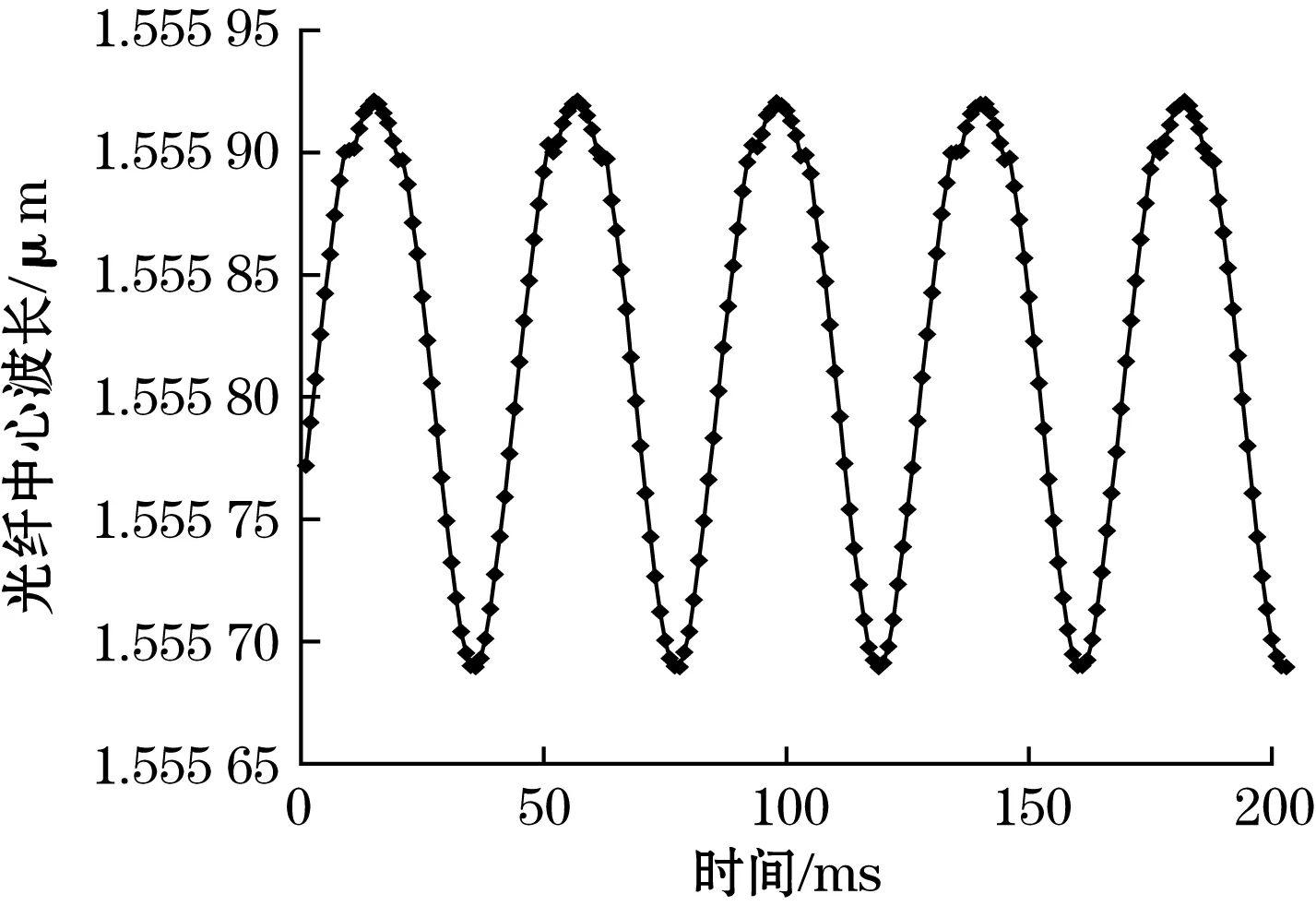
图9 传感器响应曲线

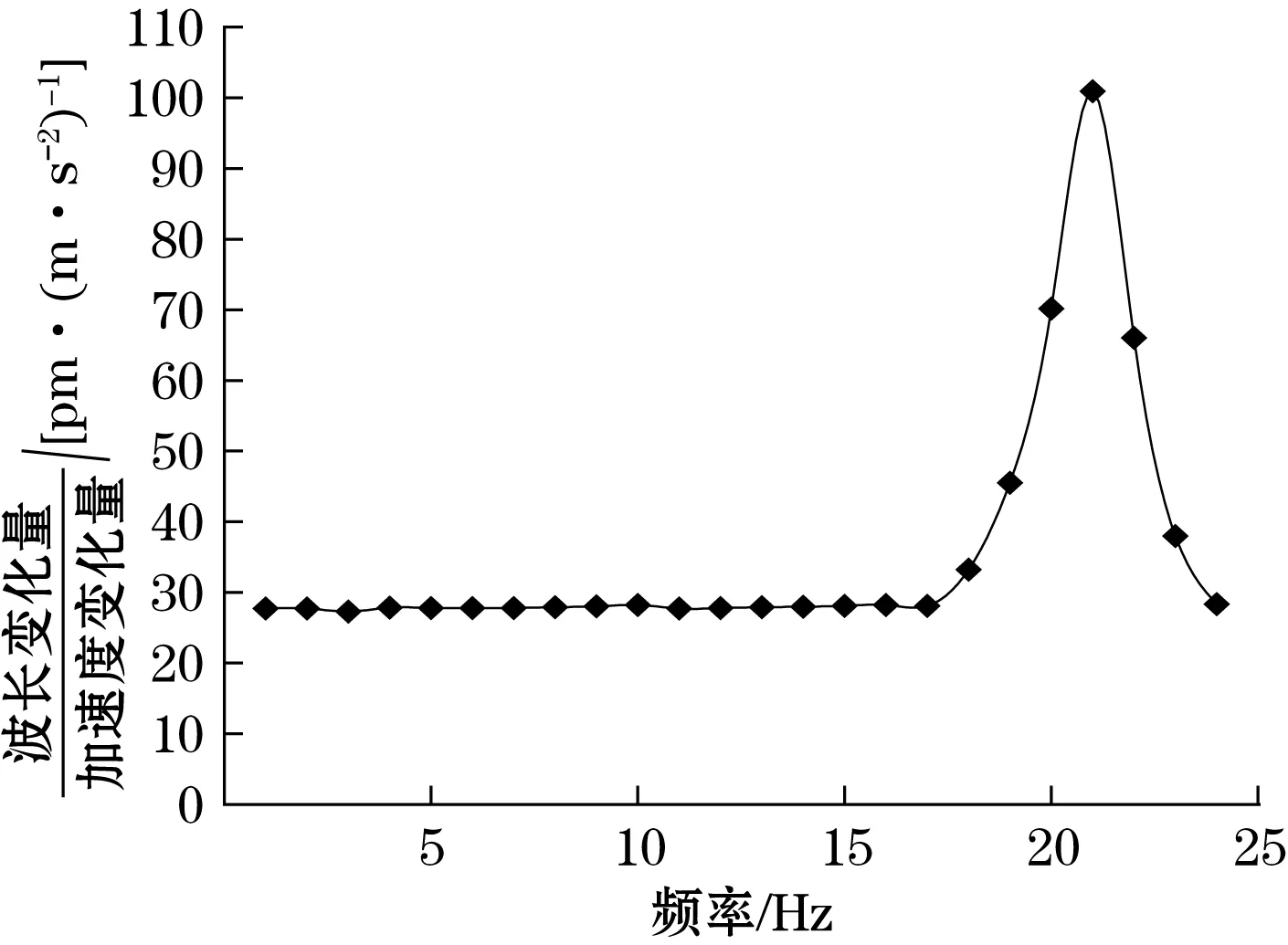
图10 第一档位的幅频特性曲线图

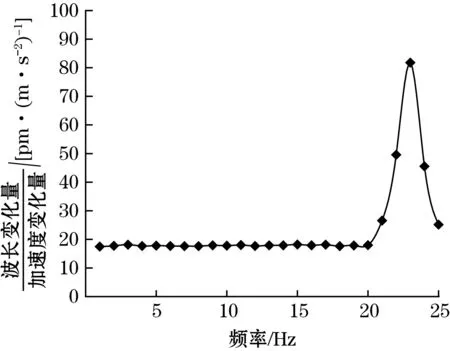
图11 第二档位的幅频特性曲线图

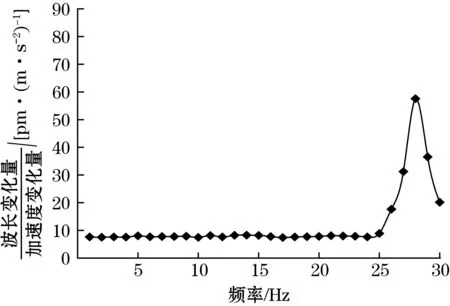
图12 第三档位的幅频特性曲线图

从以上3个图可以得出结论：在传感器的第一档位时，1～17 Hz曲线平坦、线性度较好，是传感器的幅值平坦区域，可以作为本传感器在第一档位下的工作区域。18～24 Hz为共振区，响应在21 Hz最大，说明在此频率的激励下传感器与振动台发生共振，则传感器在第一档位下的自振频率为21 Hz；同理，在第二档位时，传感器的工作区域为1～20 Hz，传感器在该档位下的自振频率为23 Hz；第三档位的工作区域为1～25 Hz，自振频率为28 Hz。

2.5 灵敏度测试实验

本光纤光栅加速度传感器的质量块有3个档位(见图5)，由1.3节的理论计算公式可得：质量块在第一档位、第二档位及第三档位时的传感器灵敏度分别为28.26、 18.84、9.42 pm/(m·s-2)。

将振动台输出设计为正弦波，振动频率固定为15 Hz，输出加速度从0.2 m/s2逐步增大到1.8 m/s2，通过解调仪可以读出光纤光栅加速度传感器在每个加速度值振动下光栅的最大波长变化量，也就是传感器的稳态响应幅值。加速度值与波长变化量之间关系见图13～图15。

图13 传感器第一档位灵敏度

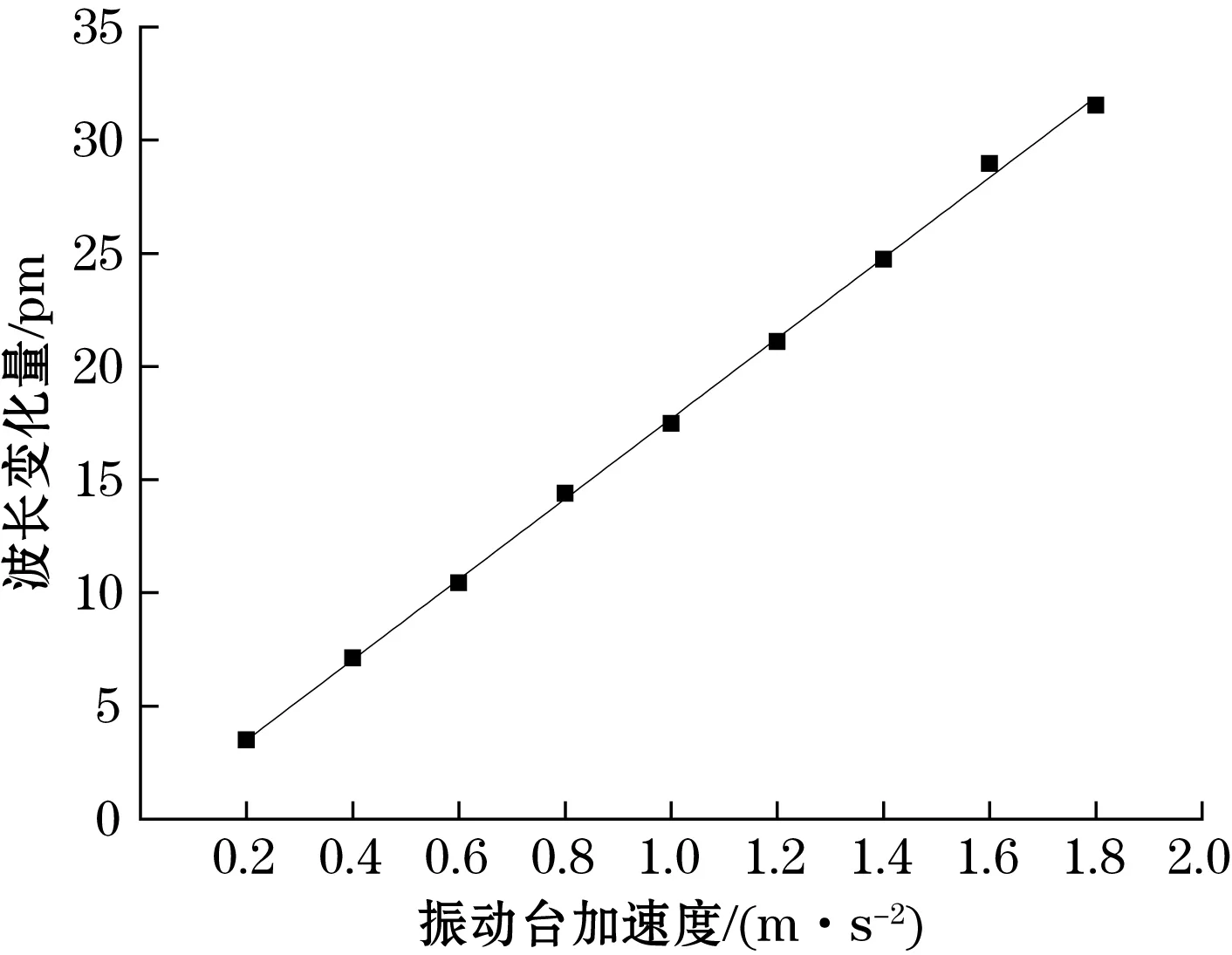
图14 传感器第二档位灵敏度

图15 传感器第三档位灵敏度

通过3个档位的实验结果可知:

第一档位灵敏度曲线的拟合公式为

y=27.703x+0.005 6

r=99.9%

则第一档位的灵敏度为27.703 pm/(m·s-2)，与理论计算值相差1.97%。

第二档位灵敏度曲线的拟合公式为

y=17.569x+0.011 3

r=99.1%

则第二档位的灵敏度为17.569 pm/(m·s-2)，与理论计算值相差6.75%。

第三档位灵敏度曲线的拟合公式为

y=7.761x+0.003 5

r=99.7%

则第三档位的灵敏度为7.761 pm/(m·s-2)，与理论计算值相差16.61%。

2.6 横向振动抗干扰测试

本光纤光栅加速度传感器为监测楼面由于人行导致的振动，需要传感器测量的是楼板竖向振动的加速度。但是在楼板由于人行导致振动的过程中，除了竖向方向的振动外，往往还伴有水平方向的振动。如果传感器对水平方向的振动抗干扰能力不足，就会严重影响传感器对楼板竖向振动加速度测量的准确性。由于本光纤光栅加速度传感器主要材料均为不锈钢，质量较大，所以有必要对本光纤光栅加速度传感器的横向振动抗干扰能力进行测试。

将传感器的拾振方向与振动台的振动方向垂直，并设计振动台的输出为正弦波，输出加速度设定为1.5 m/s2，频率范围为1～30 Hz。

实验结果如图16所示。从图16可以看出，当光纤光栅加速度传感器受到与其拾振方向相垂直的振动激励时，光栅的中心波长变化量较小，小于0.1 pm，曲线非常平稳。

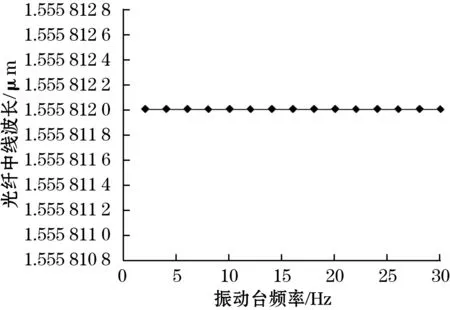
图16 传感器的横向抗干扰能力曲线

3 结束语

根据光纤光栅和等强度梁原理，研发了一种面向人致楼盖振动测试的光纤光栅加速度传感器，并利用振动台进行传感器性能实验。根据性能实验结果可知，该传感器在3个档位下的工作量程为17、20、25 Hz，灵敏度分别为27.703、17.569、7.761 pm/(m·s-2)，且横向抗干扰能力强。同时，该传感器结构形式简单，加工便利，体积合适，能够满足由于人行荷载导致的楼盖振动的测试要求，具有较高的推广应用价值。