哥德巴赫猜想成立的第三种证明方法
张尔光
(广东省韶关市人大机关,广东 韶关510600)
任何一个大于6 的偶数均可表示为两个奇素数相加之和。这就是著名的哥德巴赫猜想。
2016 年1 月,笔者在《中华少年》第3 期发表了《哥德巴赫猜想成立的两种证明方法》的文章。在该文,笔者根据哥德巴赫猜想表达的内涵,找到了破题的关键点,寻求到既能反映奇素数共同特征、又能被偶数所接受的两个表达式,进而寻求到证明哥德巴赫猜想能够成立的两种方法。
证明方法1:任何一个大于4 的偶数均可表示为两个奇素数之和。笔者研究结果表明,任何一个大于3 的奇素数均可表示为“一个小于其的素数+(2×n)之和”,又任何一个大于4 的偶数均可表示为两个奇素数之和。其证明定理为:
n= P1+P2= P1+[P1+2×(n÷2-P )]
(注:式中n 为>4 的偶数,P1、P2表示素数,P1、P2<n,P1≤n÷2)
证明方法2:任何一个大于8 的偶数均可表示为两个奇素数之和笔者研究结果表明,任何一个大于3 的奇素数均可表为“P=6×m±1”,又任何一个大于8 的偶数可表为两个奇素数之和,其证明定理为:
n=(6×m1±1)+(6×m2±1)(式中n>8)
两种方法的证明结果表明,哥德巴赫猜想成立。
最近,笔者受一道数学奥数题的启发,将哥德巴赫猜想表达的内涵与本人发现的组合数学的循序逐增原理联系起来,发现了证明哥德巴赫猜想成立的第三种方法。
1 我对哥德巴赫猜想的解读及第三种证明方法的设定
哥德巴赫猜想表达的内涵是,任何一个大于6 的偶数均可表示为两个奇素数之和。我们已知,奇素数是奇数的一部分。又知,任何一个大于6 的偶数均可表示为两个奇数之和。根据这两个已知的事实,对哥德巴赫猜想证明可作这样的解读:对“任何一个大于6 的偶数均可表示为两个奇素数之和”的证明,实际上就是验证在“任何一个大于6 的偶数均可表示为两个奇数之和”的等式中,是否均存在“其两个加数同为奇素数”的等式。如果所有大于6 的偶数的“两个奇数相加的等式”中,均存在“其两个加数同为奇素数的等式”,那么,证明哥德巴赫猜想成立;如果某个偶数的“两个奇数相加的等式”中不存在“两个加数同为奇素数的等式”,那么,证明哥德巴赫猜想不成立。又换言之,对哥德巴赫猜想的证明,就是验证所有大于6 的偶数是否全都存在于纯属于“两个奇素数之和”中,如果验证结果是肯定的,则证明成立,否则证明不成立。据此,可以说,找到了只是表达“两个奇素数之和”的方法,也就找到了证明哥德巴赫猜想的方法。本人创立的应用组合数学循序逐增原理对哥德巴赫猜想做出证明的方法,就是这样的一种证明方法。
2 组合数学的循序逐增原理
笔者研究发现,从n 个不同的元素中“按以m 个不同元素为一组”而进行的组合(不许重复),其组合过程完全是一个循序逐增的组合过程,其循序逐增的组合过程之原理,完全可以三角数阵表达出来。设S={1,2,3,4,5}为例,按以两个不同元素为一组进行组合,其循序逐增的组合过程请见下图。
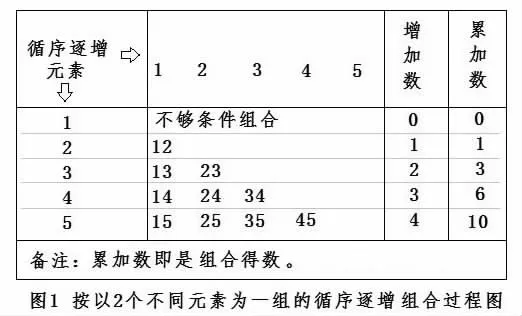
从图1 看出:其一,每一组的“两个元素”组合,均是新增元素跟前有元素的组合,且其组合组数循着元素逐增而逐增;其二,组合结果的正确表达为:12;13,23;14,24,34;15,25,35,45。从其组合结果看出,组合为一组的“两个元素”中的后一个元素数字,循着逐增元素的次序而出现。其三,“逐增数”栏和“累加数”栏的数字告诉我们,其组合的加法原则算式为:1+2+3+4=10。笔者根据“逐增数”栏和“累加数”栏的数字规律,求得其加法原则定理为:1+2+3+……+(n-1)=Cn2。在此须指出的,一些教科书将这个例题的组合结果表达为“12,13,14,15;23,24,25;34,35;45”(即以组合的“两个元素”中的前一个元素数字为序取出的表达方式),将其组合的加法原则算式表达为“4+3+2+1=10”,是有悖于组合过程中的循序逐增原理的。
3 应用数学组合的循序逐增原理证明哥德巴赫猜想成立的方法
所谓“应用数学组合的循序逐增原理证明哥德巴赫猜想成立的方法”,就是将可表为偶数之和的两个奇素数,转换为从n 个不同的元素中按2 个元素为一组组合的两个组合元素,再将这两个已转换为组合元素的奇素数相加,以求得各组“两个奇素数之和”,并以三角数阵表达出来,进而从中证明哥德巴赫猜想是否成立。
现以证明偶数“6 至100”为例。第一步,将“3 至100”范围内的奇素数当作组合元素,并以三角矩阵将其两个奇素数的组合依序列出。见图2。
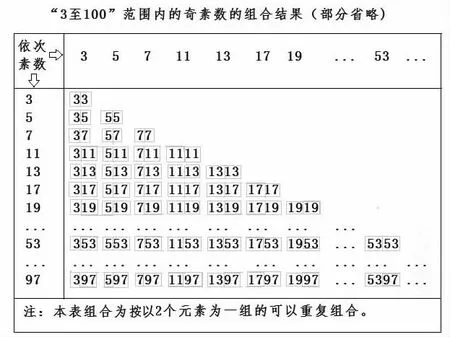
图2
第二步,计算出各组组合的两个奇素数相加之和,并以三角矩阵表达出来。见图3。
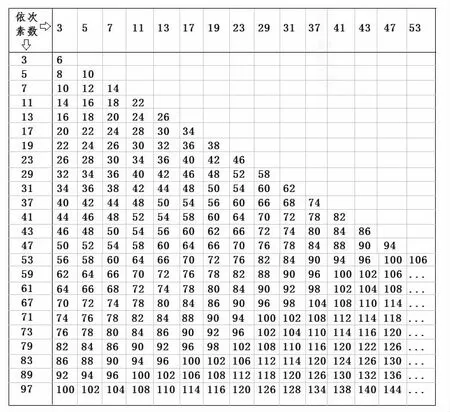
图3
从图2、图3 可看出:
奇素数3 为重复元素时,其和为6;5 与3 两个奇素数之和为8,奇素数5 为重复元素时,其和为10;7 与3 两个奇素数之和为10,7 与5 两个奇素数之和为12,奇素数7 为重复元素时,其和为14;11 与3 两个奇素数之和为14,11 与5 两个奇素数之和为16,11 与7 两个奇素数之和为18,奇素数11 为重复元素时,其和为22;其余略。
为让人们对图2、图3 的“两个组合元素(即两个奇素数)之和”中存在“6 至100”偶数出现的次数有准确的了解,笔者进行了统计,见图4。
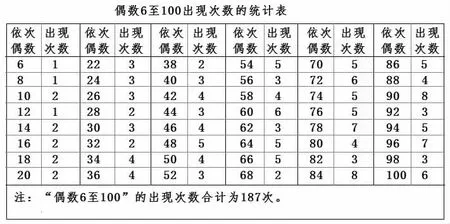
图4
从图3、图4 看出:其一,“6 至100”的各个偶数均存在于“两个奇素数之和”中,不存在漏缺现象。出现次数最低的是一位数的偶数“6 和8”,各为1 次;偶数10 起,出现次数均在2 次以上,最高的为84、90 此两个可被6 整除的偶数。其二,偶数越大,其在“两个组合元素(即两个奇素数)之和”中出现的次数越多。其三,可被6 整除的偶数,其在“两个组合元素(即两个奇素数)之和”中出现的次数,比与其左右邻近的偶数要多。第三步,验证。即是检验“6 至100”范围内的偶数在两个奇素数相加之和中有无漏缺。经将“6 至100”范围内的偶数与“3 至100”范围内的奇素数相加之和进行检验核对,验证结果:图3 所表达的“两个组合元素(即两个奇素数)之和”中,均可找到“6 至100”范围内的偶数,不存在漏缺现象。可见,哥德巴赫关于“任何一个大于6 的偶数均可表示为两个奇素数相加之和”的猜想成立。此证。
4 与证明结论有关的数字依据
为着更有力证明这种证明方法的可靠性,本人对“6 至1000”范围内的偶数在“两个组合元素(即两个奇素数)之和”中出现的次数进行了统计。见图5。
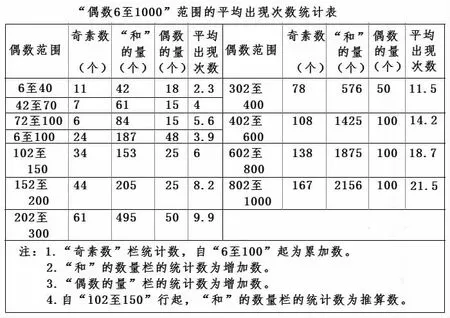
图5
从图5 看出:其一,偶数越大,其在“两个组合元素(即两个奇素数)之和”中出现的次数越多。其二,可被6 整除的偶数,其在“两个组合元素(即两个奇素数)之和”中出现的次数,比与其左右邻近的偶数要多。上述“其二、其三”两种情况,与本人在《哥德巴赫猜想成立的两种证明方法》所研究的结果相一致。它有力证明第三种证明方法得到的结论是可靠的。
在此,笔者要说的,第一,应用组合数学的循序逐增原理,将“其和”为偶数的两个(加数)奇素数转换为两个组合元素,并求得各组两个组合元素(即奇素数)之和,在方法上,它是一种可穷尽的方法,即是可将“两个奇素数相加等式”穷尽表达的方法。
第二,本人研究结果表明,偶数越大,其在“两个组合元素(即两个奇素数)之和”中出现的次数越多(即其表示为“两个奇素数相加等式”越多)。因此,当我们已知道一位数的偶数“6 和8”可表示为“两个奇素数之和”后,没有理由怀疑两位数、三位数、四位数……更多位数的偶数不可表示为“两个奇素数之和”,更没有理由怀疑哥德巴赫猜想不成立。
第三,破解数学命题,其证明方法不只一个。至于本人创立的应用组合数学的循序逐增原理证明哥德巴赫猜想成立的方法,究竟算不算得上一种证明方法?这有请数学权威来做定论了。

