四面体可展单元机构组网分析

杨 斌，郭金伟，张 雷，韩 博，陈亮亮，许允斗,3

（1. 中国空间技术研究院 西安分院，西安 710100；2. 燕山大学 河北省并联机器人与机电系统实验室，秦皇岛 066004；3. 燕山大学 先进锻压成型技术与科学教育部重点实验室，秦皇岛 066004）

引 言

空间可展开结构具有折展能力，并且可以通过使用多个预定配置和通过已知路径的运动，以受控和安全的方式可预测地展开，这些特点使得其在航空航天领域获得应用[1-4]。大型空间可展开天线作为航空航天领域关键设备，在通信卫星、深空探测等领域的成功应用及快速发展，得到了越来越多科研机构及学者的关注与研究，其理论技术研究日趋成熟。

一般地，大部分可展开天线均由基本模块或基本单元通过特定连接形式形成可展开支撑机构，然后在支撑机构上覆盖金属反射网形成天线工作表面。近年来，国内多所科研机构及学者设计并研究了多种空间可展开天线机构，取得了诸多研究成果。中国空间技术研究院西安分院研制的四面体单元构架式可展开天线[5]，突破了该类型天线的展开机构、型面成形与保持等关键技术。张京街[6]和关富玲等[7-10]针对四面体单元可展天线机构、六棱柱单元可展天线机构及单、双层环形可展天线机构，对其结构设计、组网形式及展开运动进行了较为全面的分析。陈国辉等[11]设计了一种伞状可展开天线，研究了天线在轨展开、型面及适应性等技术难题，并将其应用在“嫦娥4号”中继星。哈尔滨工业大学在大型空间可展开天线的构型设计和地面卸载方法等方面做了深入探索和大量研究工作，目前已经成功研制出索杆式伸展臂和三棱柱单元构架式伸展臂等多个样机[11-14]。西安电子科技大学在星载环形及构架式折展天线的动力学、型面设计、运动仿真及参数化程序建模等方面取得了突出成果[15-16]。文献[18-21]针对棱锥可展单元进行了设计与研究。

可展机构的组网方法研究关键在于根据可展机构的运动要求确定基本几何单元及其运动性质，以及单元之间的连接形式。现有文献针对特定可展机构的组网进行研究，如ETS-Ⅷ构架式可展开天线[22]采用六边形单元组合形成；“和平号”空间站应用了四面体可展单元组网形成的构架式可折展天线；AstroMesh环形桁架式可折展天线[23]，包含了多个对角位置连杆可以改变的平面折叠单元。Grünbaum等[24]研究了正规统一组网、k-规范组网、等边过渡性组网和非边对边组网四种正多边形的组网形式，对其组网便利条件和限制条件进行对比研究。陈焱[25]根据Bennett机构、Hybrid机构和Bricard 3种传统机构的几何特点和运动特点，设计相应的组网方式获得了数种平面、曲面折展机构。Tanaka等[26]以剪叉式单元作为基本单元，利用几何方法实现了最小组合单元机构的组网，最终得到了7种大型组网可展机构。刘行[27]基于平面密铺理论，分析了三叉Bricard机构的两种组网方式。王伟[28]分别基于单个独立的Bennett机构与剪叉式组合Bennett机构组网设计单自由度模块和多自由度模块，进而得到多种大尺度曲面可展机构。Wang等[29]对模块化大型可展天线中的组网形式及结构特点进行了设计与分析。

大型折展机构的组网研究不仅是难度大的几何数学问题，更是复杂过约束机构的机构学问题，当折展单元按照特定的机构学原理连接，最终形成的空间大尺度折展机构属于复杂空间机构。现有文献针对构架式可展天线的组网设计方法较少且存在一定局限性。因此，本文主要研究基于四面体基本单元的可展开天线支撑机构的组网方法，分析组网机构的收拢展开过程。

1 四面体基本可展单元机构组网原理

3RR-3RRR四面体基本可展单元机构简图如图1所示，其由3个底花盘、一个顶花盘、连接顶花盘与底花盘的3根腹杆和底花盘两两之间互相连接的6根同步杆组成，3个底花盘中心处于同一平面上。3个底花盘分别沿花盘中心与3个底花盘所在外接圆中心的连线方向朝目标轴线运动，实现四面体机构的同步收拢与展开运动。顶花盘P相对于底花盘（如花盘A）的运动为绕外接圆在该花盘中心点处的切线方向的转动。连接3个底花盘中心，形成平面三角形。三角形属于稳定性高的基本几何单元，且正常情况下，利用多个三角形单元均可等效组合形成任意曲面，因此本文将利用四面体可展单元的3个底花盘中心连接形成的三角形平面实现天线抛物面型反射面的逼近，其组网原理如图2所示。采用抛物面口径的内接六边形为外轮廓，将该内接六边形划分为多个三角形单元，三角形单元之间公用节点和边线。

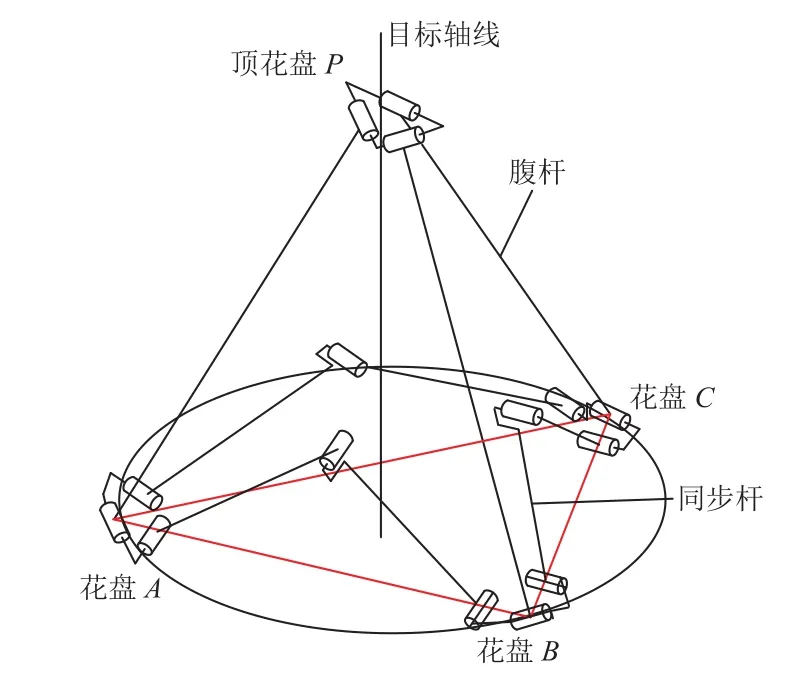
图1 四面体基本可展单元机构Fig. 1 Tetrahedral deployable unit mechanism

图2 组网原理Fig. 2 Networking principle

2 四面体可展单元机构组网方法

2.1 基本可展单元机构分布形式

四面体基本可展单元是由3个底花盘和一个顶花盘形成的棱锥结构，在其3个底花盘中心所确定的三角形平面逼近抛物反射面的组网方式中，依据三角形平面的排布特点，提出如图3所示的连续式和间隔式两种组网形式。为了增加支撑机构的整体刚度，当基本可展单元的底花盘组网形成近似的旋转抛物面之后，需要在可展单元的顶花盘之间添加连接支链，形成特定曲面，如图4所示。由上述可知顶花盘之间的连接形式对应也分为连续式和间隔式分布两种。对于由底花盘逼近形成的曲面属于天线的工作面，在其上铺设金属网后进行信号的识别与收集，可称其为反射面。而顶花盘之间添加支链后所逼近形成的曲面主要起增加机构刚度的作用，因而称其为背面。

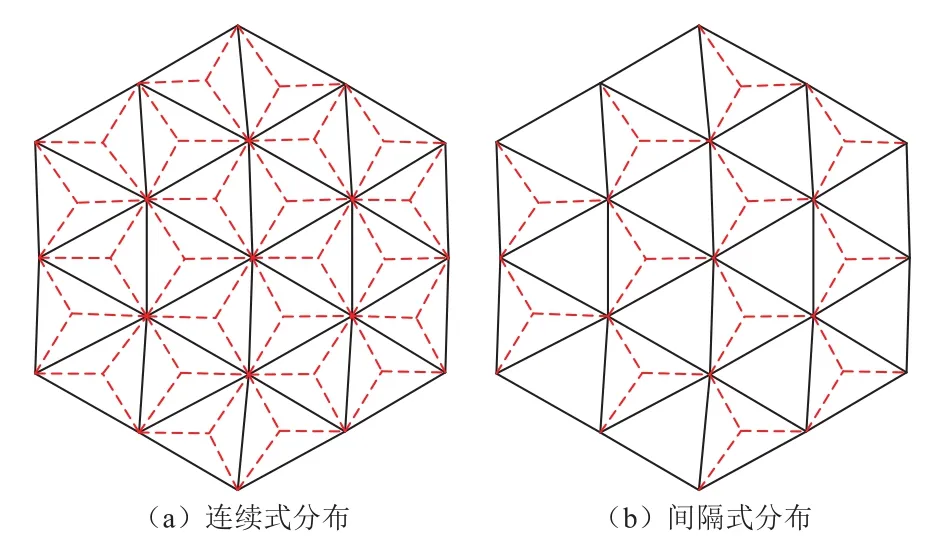
图3 反射面基本单元分布形式Fig. 3 Distribution form of the basic unit of reflector

通过观察图4中背面基本单元分布形式，存在一定分布规律：连续式背面基本单元分布如图4（a）所示，连接各顶花盘之间的支链呈现出六边形分布规律，并且各个六边形连续分布。而间隔式背面基本单元分布如图4（b）所示，连接各顶花盘节点，则背面呈现出三角形连续分布规律，与连续式反射面基本单元分布一致。在形成的三角形平面中，也可分为两类，有腹杆连接和无腹杆连接，且呈现出间隔式分布规律。而对于有腹杆连接的三角形平面，3个背面相邻的顶花盘和一个反射面对应位置的底花盘便形成了一个四面体基本可展单元机构，不同的是该四面体机构是倒置的。其分布形式与间隔式反射面基本单元分布一致。

图4 背面基本单元分布形式Fig. 4 Distribution form of the basic unit on the back

2.2 最小组合单元机构组网

根据天线抛物面组网原理，每个三角形都是通过两两共用边连接，如图5所示，从单个节点出发，这里以中心节点A为例，与其相连的三角形为6个，形成了一个六边形闭环机构。由于以每个节点为中心均能找到这样的一个闭环机构，因此选取此闭环机构为最小组合单元。而为了方便进一步分析两种基本单元分布规律的特点，将各选取中心位置的一个最小组合单元进行分析，如图6所示。

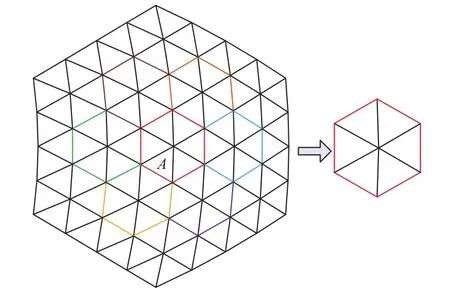
图5 选取最小组合单元Fig. 5 Selection of the minimum combination unit

在连续式最小组合单元中，6个四面体基本可展单元连续分布，单元之间共用花盘和同步杆。连接6个基本单元的顶花盘即在背面形成了六边形，将该六边形通过六根腹杆与位于反射面上的中心花盘A连接，则形成倒置的六棱锥结构，如图6（a）所示。分析该六棱锥的运动形式为，在四面体单元O-ABC中，节点O相对于节点A的运动为绕某方向的转动，该方向为节点A、B、C处所确定的外接圆在节点A处的切线方向，而六棱锥单元和四面体单元共用一根腹杆OA，则其运动形式由顶花盘的运动形式确定，即顶花盘绕腹杆上转动副（切线方向）的摆动恰好是倒置六棱锥单元的收拢运动，因而整个机构可以实现收拢与展开运动。在间隔式最小组合单元中，3个四面体基本可展单元间隔分布，共用一个花盘，如图6（b）所示。按照间隔式分布规律可知，连接反射面上的3个基本单元之间的3条边界支链，实则为下一圈机构的3个基本单元所有。背面通过3条支链连接3个顶花盘中心形成三角形，与反射面的共用花盘组成倒置的四面体结构。同理，倒置四面体单元的运动规律应按照顶花盘的运动规律确定，即顶花盘绕腹杆上转动副的摆动恰好为倒置四面体单元的收拢运动。

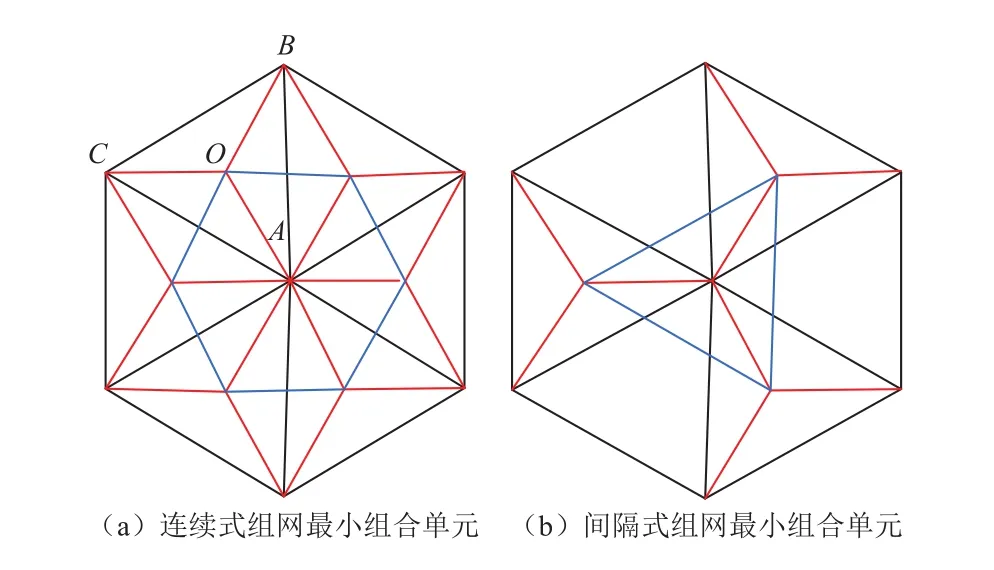
图6 两种组网形式的最小组合单元Fig. 6 The minimum combination unit of two networking forms

根据上述分析，间隔式分布与连续式分布的主要不同点如表1所示。根据表1可得出结论，在相同的情况下，间隔式分布具有基本单元数少、单元种类单一，因而组网形成的大型机构杆件较少、重量较轻的优点，因此本文主要研究间隔式分布规律的组网形式。

表1 两种基本单元排布形式翻译

3 间隔式组网机构运动分析与仿真

为了保证由四面体基本可展单元机构组网后形成的机构可以实现收拢、展开运动，并且具有较大的收拢率，需要对组网机构的运动特性进行分析，确定各构件的运动特点，从而避免机构在运动过程中出现构件干涉问题。根据2.2节的分析，本文选取间隔式分布组网形式进行可展机构的设计，对间隔式最小组合单元机构进行运动分析。在间隔式最小组合单元中，3个3RR-3RRR四面体基本可展单元共用中心节点A，呈间隔分布，两两之间通过下一层的3个基本单元的3根RRR支链相连。为了使背面上倒置的四面体单元同反射面单元的运动规律一致，选用RRR支链连接背面的顶花盘，整体结构简图如图7所示。

图7 间隔式最小组合单元机构简图Fig. 7 Schematic diagram of the spaced minimum combination unit

根据文献[20]可知单个3RR-3RRR四面体基本可展单元机构具有1个自由度，因此，当3个基本单元共用中心花盘时形成的机构的自由度为3。将3条RRR支链连接在3个顶花盘之间，形成倒置四面体单元A-HIJ，该四面体满足反射面四面体单元的相同的几何关系，且其收拢运动取决于反射面四面体单元的收拢运动，可认为是跟随运动，机构自由度不变。最后在反射面3个基本单元之间添加RRR支链，以节点A、B、G形成的闭环机构为例，由于花盘B、G的运动由各自所在的基本可展单元决定，此闭环机构可等效为图8所示的机构。

图8 平面等效机构Fig. 8 Plane equivalent mechanism

以花盘A为定平台，花盘B为动平台。在花盘A的中心建立坐标系A-XYZ，X轴沿着3个转动副轴线方向，Z轴垂直于ABG平面，Y轴由右手螺旋定则确定。则花盘B与花盘A之间通过两条支链连接，分别为P1支链和R1R2R3P2支链。根据反螺旋理论，分支P1和分支R1R2R3P2提供给定平台的约束螺旋系分别为

其中：(xp1yp10)为移动副P1在坐标系A-XYZ中的坐标。根据式（1）和式（2），沿Y轴和Z轴的约束力偶为该闭环机构的公共约束，不存在冗余约束和局部自由度，因此，根据修正的G-K公式，可得该机构的自由度为

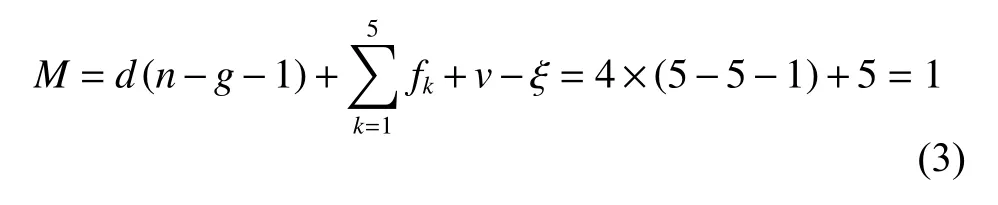
其中：M为机构的自由度数目；d为机构的阶数，且d=6-λ，λ为机构的公共约束数目；n为构件数（包含机架）；g为机构中包含的运动副个数；fk为第k个运动副具有的单自由度数目；v为机构中的冗余约束数目；ζ为局部自由度数目。

根据对基本单元组网规律及平面等效机构的分析结果，由于背面倒置的四面体单元不影响整个组网机构的自由度，分析整个机构的运动过程时可不考虑腹杆和背面结构，因此，仅考虑机构的反射面，整个最小组合单元的等效机构，如图9所示，各顶点代表反射面花盘，各顶点之间通过移动副连接。将节点A视为机架，选取任意一个移动副添加驱动，整个机构进行同步收拢，根据相似三角形原理有。因此，最小组合单元机构的自由度为1，能够实现同步收拢与展开。

为了验证间隔式组网方法的理论分析正确性和运动可行性，设计并绘制间隔式最小组合单元机构的三维仿真模型。图10为机构的一般展开状态，由于机构完全展开状态为奇异位形，需要添加多个驱动使其运动到一般展开位形。应用ADAMS动力学仿真软件进行机构的运动仿真分析，根据理论分析结果，间隔式最小组合单元机构自由度数即为实现运动的驱动数，因此，在机构的任一转动关节处添加驱动，机构运动结果如图11所示。

图9 最小组合单元等效机构Fig. 9 Equivalent mechanism of the minimum combination unit

图10 最小组合单元机构三维模型Fig. 10 Three-dimensional model of the minimum combination unit

图11 最小组合单元机构收拢状态Fig. 11 Folding state of the minimum combination unit

图10中，添加的转动驱动值为1.5°/s，分别选择多个位置添加驱动，均可实现图11所示的机构收拢状态，反之，通过添加相反方向的驱动，亦可实现机构的展开运动。仿真结果验证了基于3RR-3RRR四面体基本可展单元构造的间隔式组网机构能够实现收拢与展开运动，且自由度为1。

4 结 论

1）根据3RR-3RRR四面体基本可展单元的特点，按照三角形等效逼近的组网原理，对曲面可展开天线机构进行组网研究，提出了连续式和间隔式两种组网方法。

2）两种组网方法对比分析结果表明，基于间隔式组网方法的可展机构具有包含的基本单元数量少且种类单一、机构整体杆件少、重量轻等优势。

3）理论及仿真分析表明，采用间隔式组网方法得到的最小组合单元组网机构，能够实现同步收拢和展开运动，且自由度为1。该组网方法可以根据不同的尺寸进行组网，形成任意的曲面可展机构。