着陆器足垫冲击月壤动态行为离散元仿真分析

林云成，李立犇，赵振家，张荣荣，金 聪，邹 猛

（1. 北京空间飞行器总体设计部 空间智能机器人系统技术与应用北京市重点实验室，北京 100094；2. 吉林大学 工程仿生教育部重点实验室，长春 130022）

引 言

月球探测及其资源的开发利用离不开着陆器，而足式着陆机构不仅能起到减少冲击能量的作用，更能够起到保护其内部精密仪器的作用，从而保证月球探测器的安全性和稳定性[1]。足式着陆器的软着陆可简化为3个过程：首先，着陆腿竖向冲击月壤过程；其次，着陆腿水平滑移过程；最终，达到力平衡。着陆过程中，足垫是直接与月壤接触的部件。因此，针对着陆器足垫冲击月壤的研究，国内外学者从缓冲器材料、缓冲腿结构、等多方面分析了着陆器着陆过程的冲击力学问题。针对缓冲腿、足垫与月壤相互作用方面，试验表明了冲击能量越大，刺入深度和轴力也越大，月壤密实度对冲击加速度影响峰值较大。

着陆器在着陆过程中，由于月面凸凹不平且具有一定坡度，加之着陆器在着陆时有一定的俯仰角，因此足垫在接触月壤的实际情况中，往往与月面呈一定的倾角。目前，研究足垫与月壤二者相互之间的力学关系较多是足垫以垂直方向冲击月壤。

文献[2]提出针对触地机关软着陆稳定性分析，建立了新型探测器的ADAMS（Automatic Dynamic Analysis of Mechanical Systems）动力学分析模型，并引入变推力主发动机及姿控推进器的推力控制模型。文献[3]讨论了新型着陆器在自由落体着陆和低速着陆两种着陆方式下的着陆稳定性，建立了新型着陆器的动力学分析模型，对着陆过程进行了仿真。文献[3-4]讨论了着陆腿和着陆工况对着陆性能的影响。吴晓君等[6]基于对着陆过程的研究，将问题分解为垂直冲击和水平滑动两个方向的运动，并通过力的平衡和动量定理建立了垂直冲击的动力模型。利用独立研发的垂直冲击模型试验装置，探讨了冲击过程中土体密实度、冲击速率和冲击质量等对足垫刺入深度、最大轴力和最大加速度等的影响。试验结果与动力模型进行了对比，结果表明：动力模型能合理地反映出着陆器在垂直冲击阶段的动力特性。文献[6-7]讨论了着陆器足垫冲击月壤的模拟试验。文献[8]给出了着陆动力学分析的数学模型，并在分析铝蜂窝材料缓冲特性的基础上，建立了铝蜂窝缓冲器模型，将其应用于软着陆机构单条着陆腿冲击仿真。文献[9]讲述了机械动力学软件在在月球着陆器建模中的应用。文献考虑月球1/6 g的低重力环境和月壤物理力学性质的影响，以及真实地面环境下无法进行大量的冲击试验来研究足垫冲击月壤后对月壤的影响情况。龙铝波等[10]建立了着陆器足垫–月壤相互作用模型及铝蜂窝的力学模型，在此基础上应用ADAMS软件构建准确的着陆器整体的多体动力学模型，并结合力–角稳定性度量法，为着陆器安全软着陆提出了合理的稳定性判据。该文章着重分析了月面着陆环境和初始条件对软着陆稳定性的影响，并获得了着陆器发生倾覆时不同着陆偏航角与极限水平速度关系的稳定性边界曲线。刘焕焕[11]建立了包括三腿、四腿月球探测器下坡软着陆的二维动力学方程，并对着陆过程中缓冲器的力学特性、足垫与月表的相互作用和着陆过程进行了数学描述。借助所编制的仿真软件，对月球探测器的二维软着陆动力学进行了仿真，对各种着陆条件参数，以及探测器的总体参数，如探测器的回转半径对着陆过载系数、稳定性和着陆腿压溃长度的影响进行了参数敏度分析。黄晗等[12]研究了土壤类型和密实度，脚垫直径和冲击高度对脚垫冲击性能的影响，结果表明，土壤类型和压实度对冲击深度的影响最大，其次是脚垫直径，然后是冲击高度，验证了所提出的模型能够准确预测脚垫峰值冲击力。Shuai等[13]建立了考虑地面弹性变形的联合仿真动力学模型，用于着陆器着陆冲击过程，并通过单腿着陆冲击试验验证了该模型的有效性，结果表明，降低水平着陆速度可以有效地降低着陆器水平着陆过载，提高着陆稳定性。Zheng等[14]提出了模型的能量和质量平衡准则，并结合理论和计算方法，该模型中的缓冲能量吸收特性具有良好的能量吸收能力，其中可以消散高达84%的初始能量。梁绍敏等[15-16]对着陆过程中足垫与月壤的相互作用进行了研究。

本文建立了具有角度的足垫冲击月壤的动态作用力学模型，通过离散元仿真分析对足垫冲击月壤的动态过程做了分析，研究冲击速度、冲击角度对足垫受力和月壤孔隙率变化情况。

1 足垫冲击月壤模型

足垫与月壤作用力学模型是基于着陆器足垫以一定速度垂直或倾斜冲击月壤。在足垫冲击月壤时，着陆器的动量和势能被着陆器的吸能结构和月壤的变形吸收，足垫冲击月壤时受力模型如图1所示。其中：M1为冲击体总质量的1/4；θ 为冲击方向与月壤表面法向的夹角；rm为足垫的最大半径；r为足垫沿冲击方向接触月壤面积的半径（0≤r≤rm）；Ks为月壤的刚度系数；δ为足垫沿冲击方向的轴向刺入位移；δ1为足垫沿冲击方向的轴向刺入速度；δ2为锥形月壤沿着冲击方向的轴向位移；为锥形月壤沿着轴向运动速度；φ为月壤的内摩擦角；π/2−φ为锥形体月壤顶角；Ms为锥形体有效域月壤质量，其中Ms=ηρr3(δ1)。

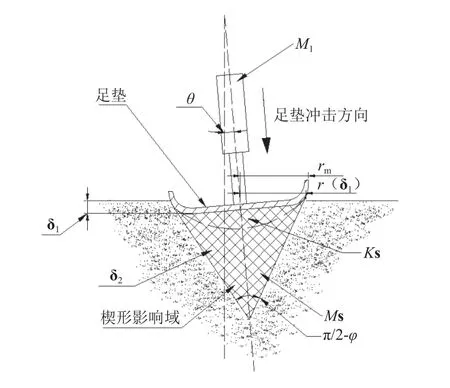
图1 足垫冲击月壤力学模型Fig. 1 Mechanical model of footpad impacting on lunar soil

根据冲击机械部分得出受力平衡方程如下

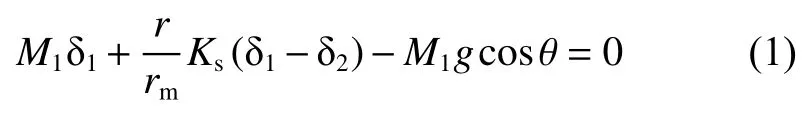
其中：g为当地实际重力加速度。

根据锥形月壤的动量定理得出微分方程如下

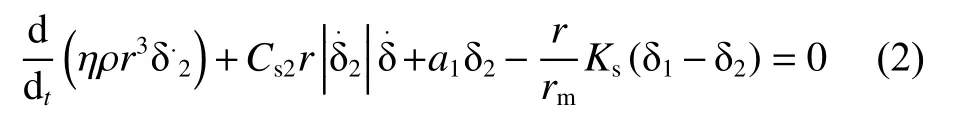
冲击动态过程为

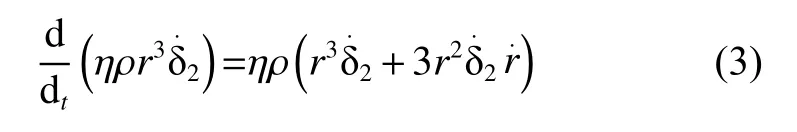
足垫接触土壤半径与入土深度变化为

将式（3）～（4）带入式（2）得到

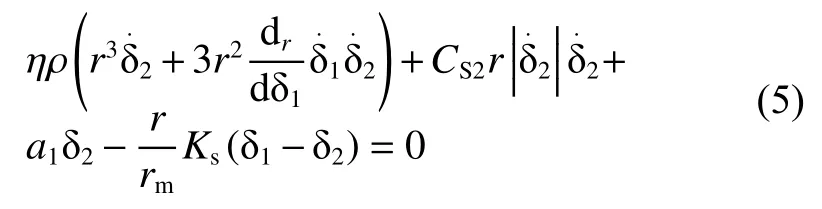
其中：ρ为月壤密度；CS2为表征足垫刺入月壤作用的锥形土体与周围月壤发生动量转移现象的系数；a1为月壤强度系数，与锥形土体有效域质量成正比。这里CS2、a1都为经验值。联立方程（1）、（5）可求得足垫在冲击中的运动与受力情况。从而得出，影响足垫与月壤相互作用力学关系的因素有4个：冲击物重量M1、冲击速度V、月壤密度ρ 以及着陆倾角θ 。

2 月壤颗粒模型

公式（5）表明，冲击角度和月壤密实度对冲击的能量的吸收具有重要影响，但通过公式计算难以准确获取月壤的动态变形和其性能变化。因此，文章采用离散元软件——PFC（Particle Flow Code）进行仿真分析。

月壤是指月球表面覆盖着的土壤，一般呈现淡褐、暗灰色。绝大多数月壤元素与地球土壤元素一致，包括氧、硅和铝等。月壤大部分由小于1 mm的具有粘聚性的细颗粒组成，颗粒大小的中间值为40～130 μm，平均大小为70 μm。月壤物理力学特性对月面探测车辆运动影响很大，包括颗粒大小、孔隙率、凝聚力、内摩擦角、容积密度、颗粒比重、颗粒形态等。其基本物理力学性质如表1所示。

表1 月壤物理力学性质Table 1 Mechanical characters of lunar soil

文章采用PFC软件分析足垫与月壤作用。根据表1月壤的物理力学性质，选用线性刚度模型建立月壤离散元模型。线性模型如图2所示，图中为切向接触力；为法向接触力；F为接触合力，并认为变形只发生在接触点处。根据力–位移接触定律可以得出两颗粒间的接触力

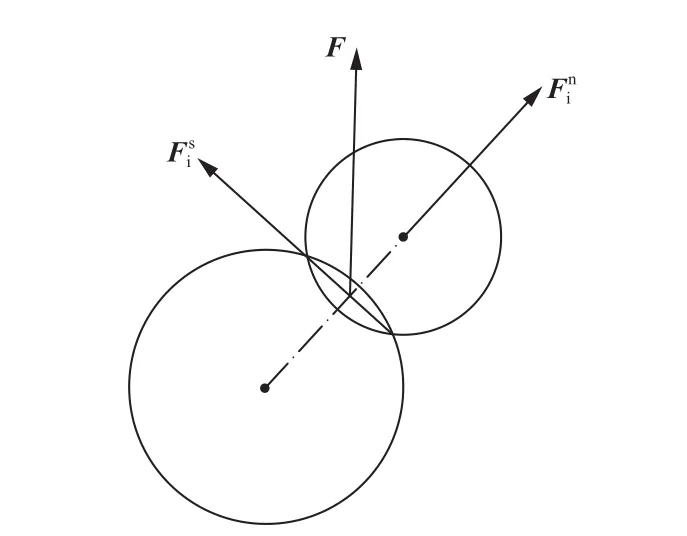
图2 线性接触刚度模型Fig. 2 Linear contact stiffness model

其中：kn为法向接触刚度；Un为法向接触位移；ni为单位法向量。

研究通过双轴模拟试验，确定颗粒接触力学参数，模拟时设定颗粒在1/6重力加速度条件下达到平衡。通过反复调整颗粒输入参数，直到模拟试验结果与月壤力学性质接近。此时，参数如表2所示。

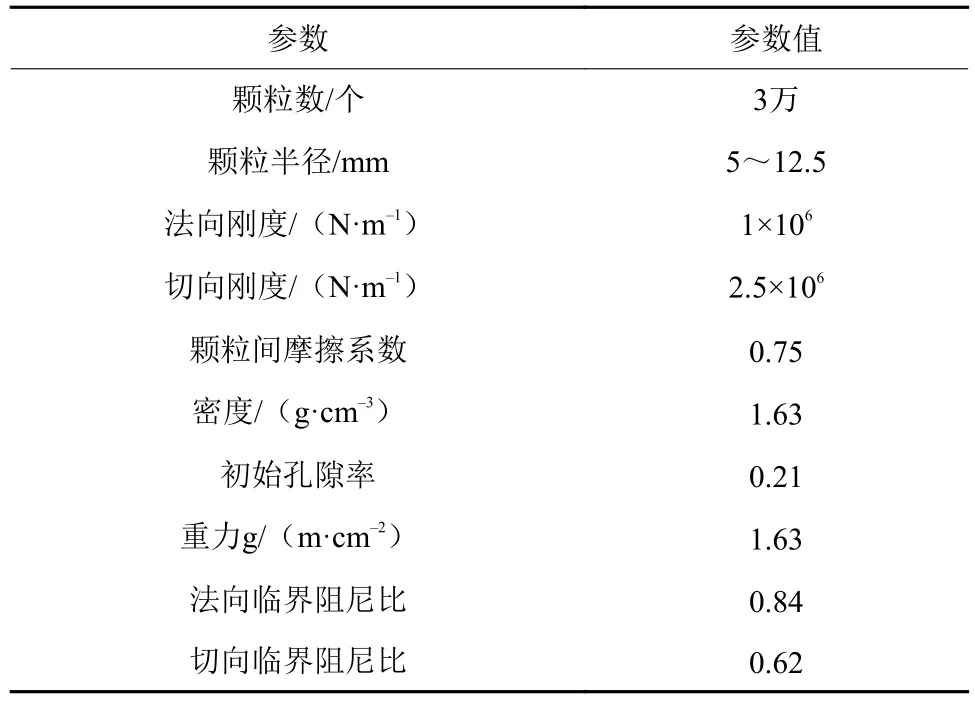
表2 月壤离散元接触力学模型参数Table 2 Contact mechanics model parameters of discrete elements in soil

此时，主应力差–轴向应变关系曲线如图3（a）所示，体积应变–轴向应变关系曲线如图3（b）所示。

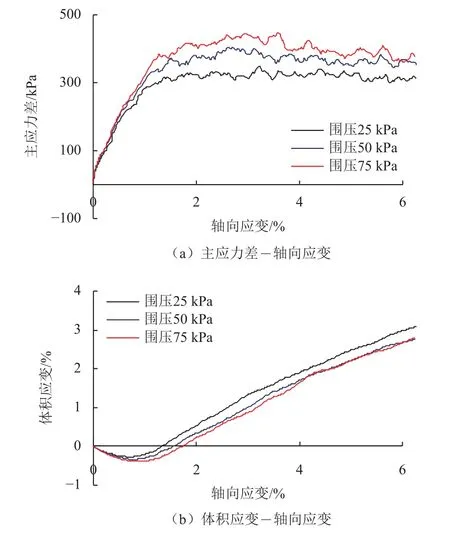
图3 离散元模拟月壤双轴试验结果Fig. 3 Biaxial test results from DEM simulation

3 结果与分析

3.1 足垫冲击月壤受力分析

着陆器着陆区域往往选择较平坦的月面，月面的坡度一般不超过10°，考虑着陆区域特殊情况，仿真过程设定4个冲击角度进行研究，角度分别为0°、8°、15°、22°。

着陆器足垫在冲击月壤时，受到月壤的反作用力，足垫会产生较大的反向加速度并在较短的时间内停止。通过PFC软件模拟时，假定受到的加速度为定值，来分析不同冲击角度足垫的受力分析。如图4为冲击速度达到4 m/s条件下不同冲击角度足垫的受力情况。

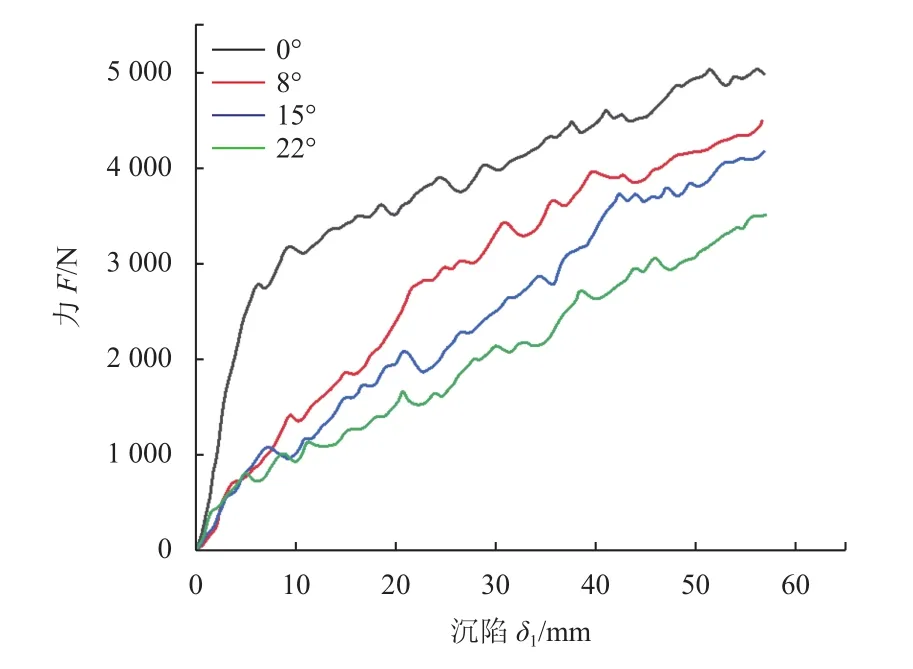
图4 完成4 m/s不同冲击角度足垫受力曲线Fig. 4 Force curve of 4 m/s footpad cushion at different impact angles

由图4分析可知，足垫在相同的沉陷深度下，冲击角度越大，足垫与月壤接触面积越小，故而足垫对颗粒的作用力较小，最终足垫受到的力也就越小。其中0°、8°、15°、22°峰值冲击力分别为5 080.6 N、4 478.8 N、4 224.9 N、3 605.9 N。冲击力峰值在0°时比8°时增加了13.4%、比15°时增加了20.2%、比22°时增加了40.8%。

图5为4个冲击角度在3个冲击速度下的冲击力峰值图，从图中可以看出，足垫受到的力随着冲击角度增大而减少。速度不同，减小的幅度不同，其中最大减幅出现在4 m/s时，0°比22°的情况下，减幅为40.8%。

图5 冲击角度与冲击力的关系Fig. 5 Relation curve between impact Angle and impact force

3.2 足垫冲击月壤的破坏

足垫在冲击月壤的过程中，会对月壤造成破坏，文章通过对月壤进行区域标记来研究足垫对月壤的破坏情况。以冲击角度22°为例，图6为不同深度下足垫刺入月壤对月壤的破坏情况。

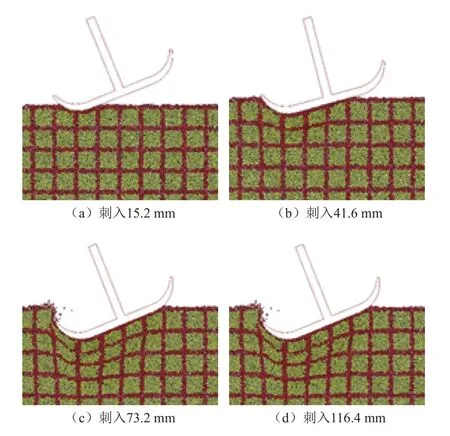
图6 不同刺入深度月壤破坏图Fig. 6 Failure maps of lunar soil at different penetration depths

从图6可以看出，随着足垫向下的刺入，对月壤的剪切破坏作用越来越大，主要表现沿着足垫垂直作用方向，对月壤进行不同程度的压实，刺入越深，压实越严重，而沿水平方向，月壤并没有切向剪切作用。

图7为0°、8°、15°、22° 4个冲击角度在相同刺入位移下的月壤破坏情况。

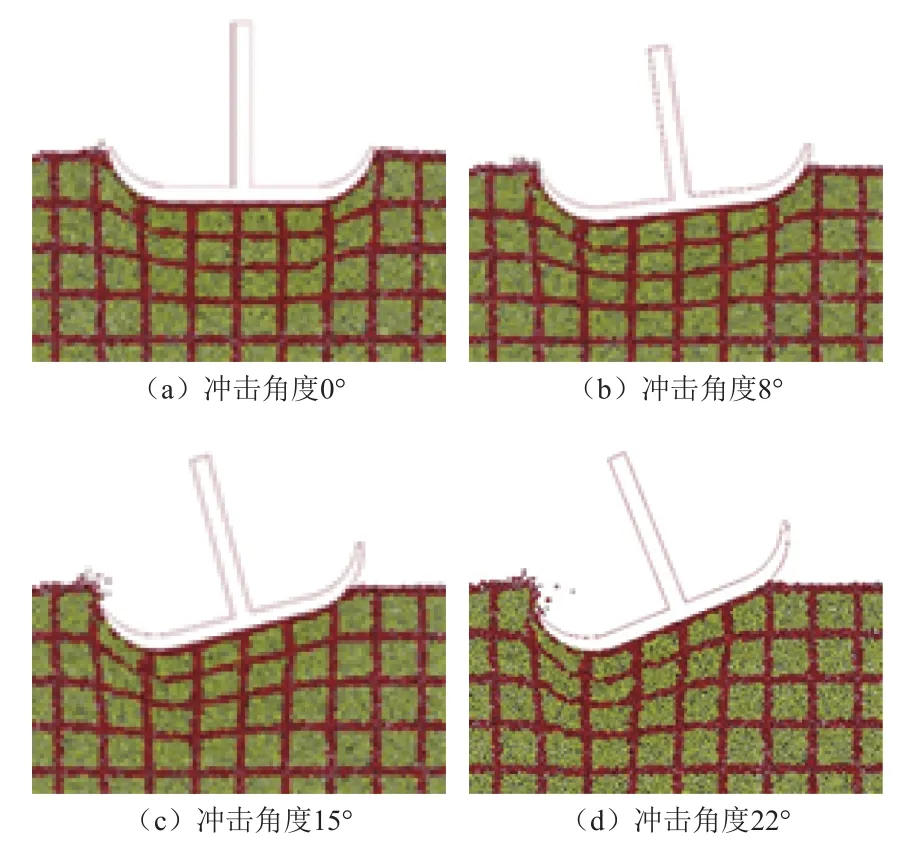
图7 不同冲击角度对月壤的破坏情况Fig. 7 Destruction of lunar soil at different impact angles

从图7可知，在沿垂直方向足垫刺入月壤位移相同情况下，随着足垫冲击月壤角度的增大，足垫与月壤的接触面积减小，而足垫刺入月壤位移大的一侧对月壤的剪切破坏程度增大。无论角度大小，对月壤的破坏主要是沿冲击方向做了不同程度的压实，而没有出现较大的沿切向方向的剪切破坏情况。

3.3 足垫冲击月壤内部力场变化

根据本文模型理论推导，足垫冲击月壤后对月壤作用形成一个圆锥形区域，从足垫作用圆型区域纵剖面来看应是一个楔形区域。通过DEM（Discrete Element Method）软件可以直观地看出足垫冲击后月壤作用的内部力场的变化情况。从而定性地分析月壤受冲击后的变化情况。图8为足垫以不同角度冲击月壤其颗粒内部接触力场图，可以看出形状接近楔形，在垂直方向相同沉陷位移情况下，冲击角度越大，足垫接触面积越小，颗粒内部接触力也越小。

图8 不同冲击角度下月壤内部接触力场图Fig. 8 Contact field diagram of lunar soil at different impact angles

3.4 足垫冲击月壤孔隙率影响

着陆器在着陆过程中，足垫接触月壤后会对月壤产生破坏并对其有一定的压实作用，月壤的固有孔隙率也随着发生变化，反映了月壤对冲击能量吸收的情况。在PFC2D中对孔隙率的定义按以下公式定义

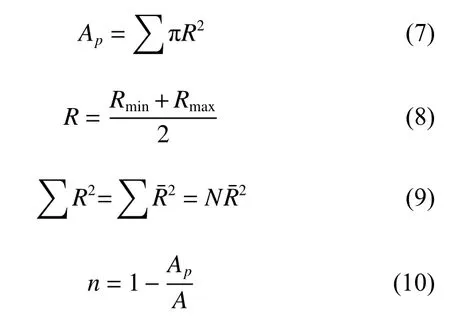
其中：A为颗粒所占据区域面积；Ap为所有颗粒面积之和；R为颗粒半径；N为颗粒数。

通过PFC2D软件对足垫作用下方定义一个半径为60 mm的测量圆进行检测分析，该测量圆圆心距离地表面120 mm。图9为足垫冲击模拟月壤测量圆示意图。

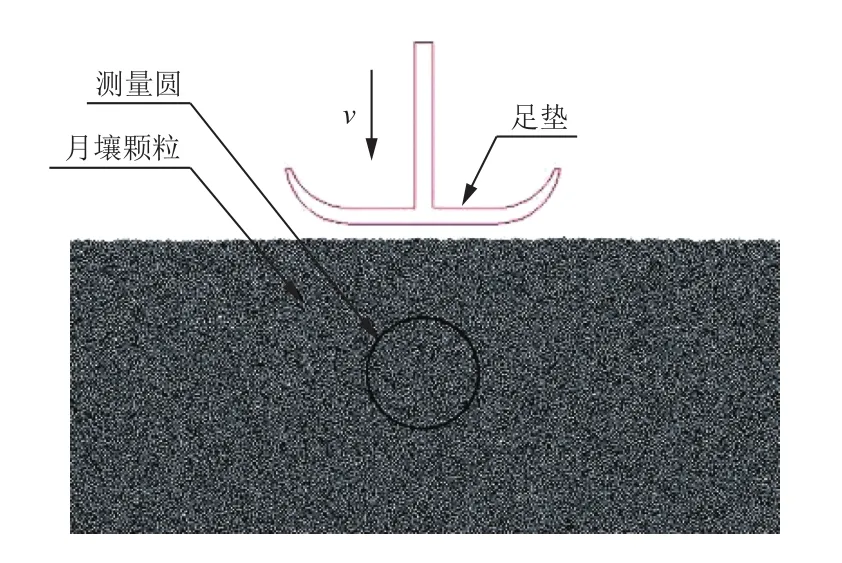
图9 足垫冲击月壤测量圆示意图Fig. 9 Schematic diagram of measurement circle of footpad impacting lunar soil

足垫冲击月壤的角度不同时，以垂直方向沉陷位移为标准，足垫对月壤的压实面积也就不同，故而足垫下月壤的孔隙率随足垫冲击角度的变化应有一定的规律。图10为冲击速度4 m/s的情况下，不同冲击角度对月壤孔隙率的影响情况。

图10 4 m/s下不同角度对孔隙率的影响Fig. 10 Effect of different angles on porosity at 4 m/s

由图10可知，角度越大孔隙率变化情况越缓慢，孔隙率变化率较小。分析得出0°、8°、15°、22°，4个不同冲击角度冲击前后孔隙率变化率分别为78.1%、64.3%、42%、26.5%，这是因为随着冲击角度的增加，单位沉陷位移下足垫接触月壤的面积减少，故而对月壤压实程度较小，孔隙率变化情况较小。

图11为冲击角度为0°时，不同冲击速度对月壤孔隙率的影响情况。

由图11可知，冲击速度1 m/s时，足垫沉陷约10 mm后，孔隙率开始变化，在速度为2 m/s情况下，沉陷约为13 mm后，孔隙率改变，而在4 m/s的情况下，则是在沉陷21 mm后，孔隙率较明显改变。分析认为：冲击速度越大，对孔隙率的改变程度越滞后。这是由于冲击速度越大，短时间内对表层月壤迅速造成破坏，月壤颗粒相互作用时间极短，而在这段时间内，较深层的月壤并没有受到破坏，故而孔隙率变化较滞后。同时，从图11中可知，冲击速度分别为1 m/s、2 m/s、4 m/s时，月壤孔隙率的变化率分别为50%、61.6%、78.1%，可见速度越大对孔隙率的影响也越大，这是因为冲击速度越大，冲击能量也越大，对月壤的压实破坏程度也越大，故而造成孔隙率变化较大。

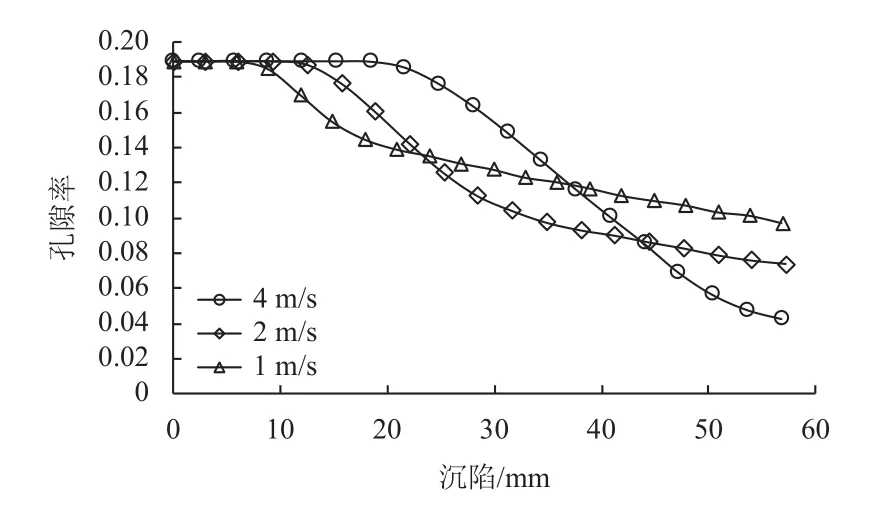
图11 0°下不同冲击速度对月壤孔隙率的影响Fig. 11 Effects of different impact velocities on the porosity of lunar soil at 0°

4 结 论

1）通过受力分析，给出了足垫冲击月壤的力学模型，该模型能够反映冲击角度和月壤密度对冲击受力的影响。

2）冲击速度越大、足垫受到的冲击力越大，在冲击速度4 m/s、冲击角度为0°时，冲击力最大为5 080.6 N。另外，在竖向位移相同的情况下，冲击角度越大冲击力越小。

3）足垫冲击月壤角度越大对月壤的压实作用越小，得出0°、8°、15°、22° 4个不同冲击角度冲击前后孔隙率变化率分别为78.1%、64.3%、42%、26.5%，其中22°时，前后孔隙率变化仅为26.5%。

4）冲击角度一定时，速度越大对月壤的压实较滞后，而压实程度较大，冲击速度分别为1 m/s、2 m/s、4 m/s时，月壤孔隙率的变化率分别为：50%、61.6%、78.1%。

5）对着陆器在着陆时选择冲击角度和冲击速度有一定的参考意义，选择合适的角度和速度来减小冲击力和孔隙率的变化，以增加着陆时的安全性和稳定性。