波形钢腹板-桁式弦杆连续梁桥受力分析
——以深圳马峦山公园高架桥为例
吴连波
(深圳市交通公用设施建设中心 广东深圳 518000)
1 课题研究缘由
波形钢腹板组合梁桥,由于自重轻、腹板不开裂、预应力效率高等优点,在工程中得到了广泛应用[1-2]。传统的波形钢腹板组合梁桥,由混凝土顶、底板及波形钢腹板组成,当底板混凝土由钢管混凝土取代时,即形成了波形钢腹板-桁式弦杆组合梁桥[3-4],如图1所示。该种结构包括混凝土顶板、波形钢腹板、钢管混凝土组成。该组合梁结构,采用混凝土顶板和下弦钢管承受正弯矩,利用钢管混凝土下弦钢管和顶板预应力束承受负弯矩,使得组合梁延性增强,自重进一步降低,方便桥梁施工。
基于波形钢腹板-多弦杆连续组合桥梁是一种新型组合梁桥,其受力性能良好,可以为新建桥梁建设提供一种选择方案,本文以深圳马峦山公园高架桥为工程背景,对该种桥梁进行受力分析,以期能为该新型组合结构的设计计算提供参考。
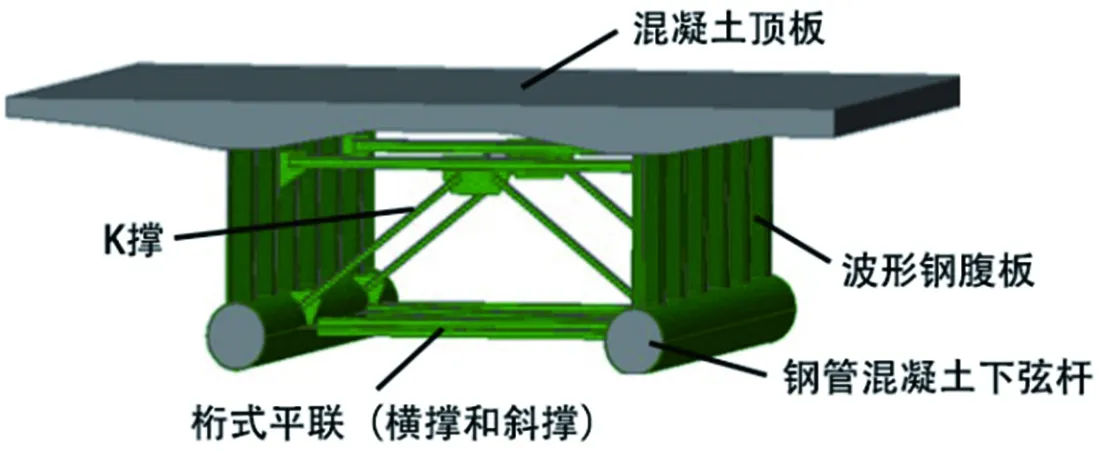
图1 波形钢腹板-多弦杆桥梁效果图
2 工程概况
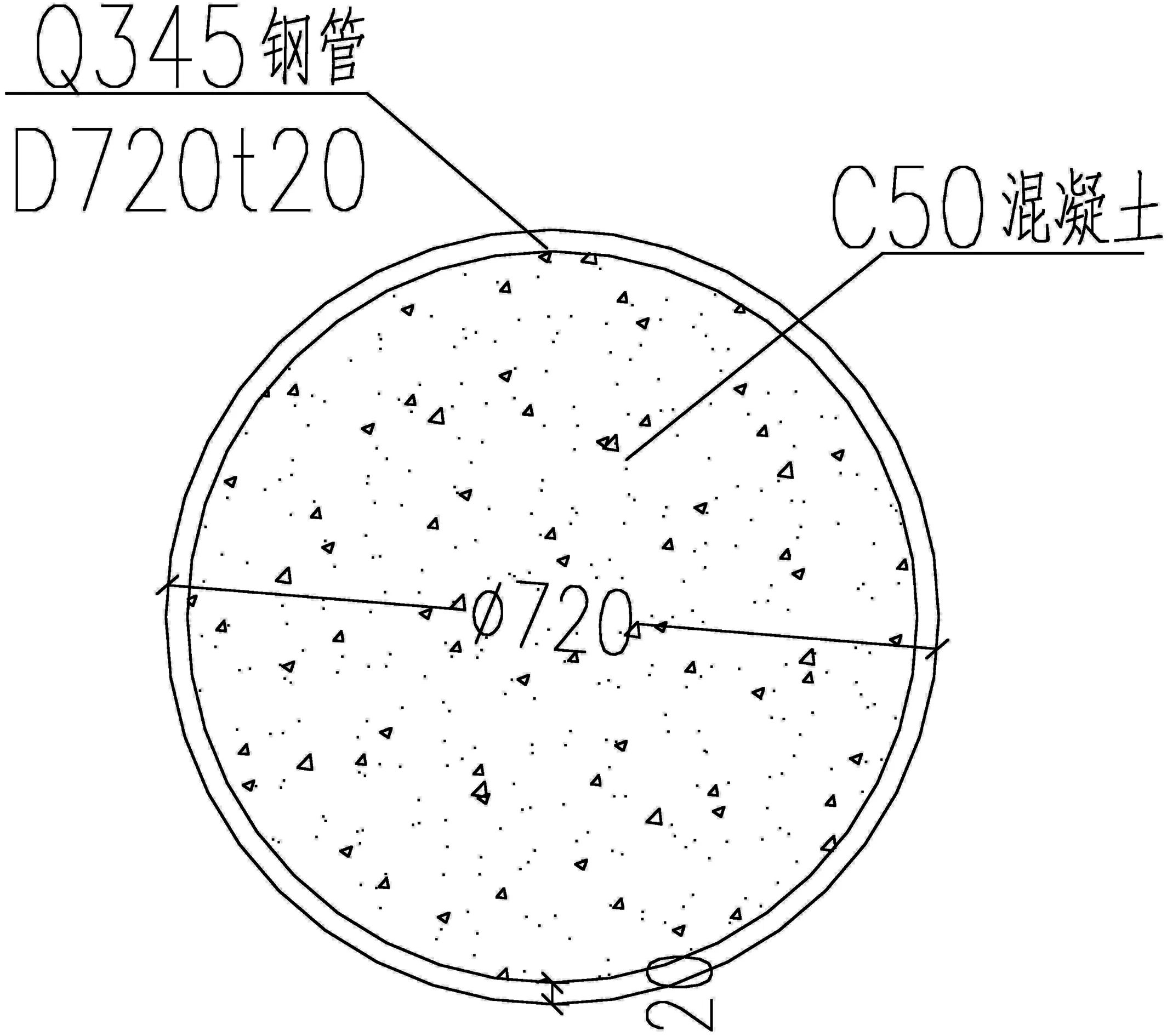
马峦山公园高架桥1号桥上部结构为波形钢腹板-多弦杆组合梁,右幅为3m×45m连续结构箱梁。道路等级为城市快速路,设计安全等级为一级,设计汽车荷载等级为城市A级。单幅桥面宽度20m,梁高2.8m。顶板为C50混凝土,底缘采用直径720mm圆钢管,内部灌注C50微膨胀混凝土,全桥腹板均采用波形钢腹板,钢材为Q345qC,板厚12mm~24mm,其形状为1600型。桥型总体布置如图2所示。各主梁通过端主梁及桁架平联连接。端横梁宽1.2m,高2.6m。平联由Ф245×10mm横杆和Ф159×10mm斜杆组成,横杆间距为4.8m,如图2(c)所示。混凝土顶板在负弯矩区内布置48束预应力钢筋(每箱24束),每束布置15φ15.24钢绞线,并采用双向张拉。波形钢腹板与混凝土板通过22mm直径的栓钉连接,波形钢腹板与钢管间采用焊接连接,波形钢腹板与波形钢腹板间采用对接焊缝连接,波形钢腹板与端横梁间通过PBL连接件连接。成桥后的效果图如图2(f)所示。

(a)标准跨立面图

(b)一般截面尺寸

(c)桁架平联

3 有限元模型建立
实体模型及杆系模型都可进行实桥分析。实体模型具有计算精度高、局部应力准确、计算速度慢的特点;杆系模型具有计算效率高、整体受力分析效果好特点,并且具有成熟的商用桥梁设计软件。本节通过波形钢腹板-多弦杆组合梁桥的实体及杆系模型的对比,验证杆系模型的准确性。
采用通用有限元软件ABAQUS建立实体模型。采用实体单元建立顶板、管内混凝土等实体结构,采用板壳单元建立钢管、波形钢腹板等薄壁结构,采用升降温模拟预应力荷载。该建模方法的可靠性已在缩尺模型分析中得到了验证[5,6]。缩尺试验如图3所示,实体模型如图4所示。

图4 实体模型
杆系模型采用桥梁专用软件MIDAS/Civil建立。下弦钢管混凝土采用共用节点双单元法进行模拟,可细分为下弦钢管与下弦管内混凝土两种单元;波形钢腹板、钢翼缘板采用梁单元建立,混凝土顶板采用梁格法建立,钢翼缘板分别连接顶板混凝土和波形钢腹板。杆系模型如图5所示。

(a)整体模型

(b)波形钢腹板

(c)下弦钢管混凝土图5 实桥杆系有限元模型
表1列出了(自重+预应力+车道荷载)组合作用下实桥杆系有限元模型与实桥实体有限元的计算结果。从表可以看出,杆系有限元模型得到的计算结果与实体有限元结果基本相同,两者比值在0.93~1.04之间,即系杆有限元模型在保证计算效率的同时可以具有较好的精度。

表1 实体有限元与杆系有限元模型计算结果
4 正常使用状态分析
4.1 下弦钢管应力
图6给出了正常使用极限状态下下弦钢管的应力包络图。下弦钢管应力在边跨L/2截面处钢管底缘出现最大拉应力,在中支点钢管底缘出现最大压应力,全桥采用三跨等跨布置,中跨钢管拉应力值较小且主要以压应力为主。钢管最大拉应力为137.4MPa,最大压应力为-234.7MPa,均拉、压应力小于容许应力±270MPa,均满足要求。

图6 正常使用极限状态下下弦钢管应力计算结果
4.2 混凝土板应力
图7给出了正常使用极限状态下混凝土顶板顶缘最大压应力计算结果。从图中可以看出,在正常使用极限状态下,除部分位置外,基本处于受压状态。中跨跨中附近及边跨边支点附近出现的拉应力由温度作用产生。顶板最大拉应力达到1.29MPa,小于最大拉应力限值1.83MPa;最大压应力为-12.6MPa,小于容许值-16.2MPa。

图7 正常使用极限状态下混凝土顶板顶缘最大压应力
4.3 组合梁刚度
图8给出了不计冲击力的车道荷载频遇值作用下主梁最大挠度分布图。在车道荷载作用下,主梁最大挠度出现在边跨跨中截面处,挠度曲线在各跨范围内均关于跨中对称。从图8的主梁挠度验算结果可以看出,主梁最大挠度为14.9mm,满足GB 50917-2013《钢-混凝土组合梁桥设计规范》中L/600的限值;当下弦钢管不填充混凝土时,主梁最大挠度22.9mm。主梁下弦钢管填充混凝土与不填充混凝土的最大挠度比值为0.65∶1。下弦钢管填充混凝土可以有效提高组合梁的刚度。
5 极限状态验算
前述的杆系模型将组合梁分为混凝土板、下弦杆、波形钢腹板等构件。由于目前没有成熟的波形钢腹板-桁式弦杆组合梁弯曲承载力计算方法。本节采用MIDAS软件对上述构件进行设计荷载下的极限承载力验算,并列出主要验算结果。

图8 不计冲击力的车道荷载频遇值作用下主梁最大挠度分布图
5.1 混凝土板
将组合梁中的混凝土板单独分析,其可以看成处于偏心受压状态的构件。这里依据JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[7],对混凝土板进行偏压验算。忽略二阶效应,所有截面均能满足规范要求。图9为最不利承载能力极限状态组合下的混凝土顶板偏压承载力验算结果。

图9 混凝土顶板偏压承载力验算结果
5.2 下弦钢管
对下弦钢管混凝土进行偏压及钢管应力验算,各验算结果基本符合设计要求。
图10为下弦钢管应力验算结果,压应力越接近中支点越大。

图10 下弦钢管应力验算
5.3 波形钢腹板
为了便于提取各梁分配的剪力,采用整梁模型计算各纵梁的剪力分配,并将其代入《波形钢腹板组合梁桥技术标准》(CJJT 272-2017),验算波形钢腹板的剪切强度、局部屈曲应力、整体屈曲应力及组合屈曲应力,各验算值均满足设计要求。图11为合成屈曲的验算结果。由于中支点处的剪力最大,该处为剪切屈曲及剪切强度的控制设计点。

图11 波形钢腹板合成屈曲验算
6 结语
实体模型及杆系模型都可以用于组合梁桥的弹性分析。波形钢腹板-多弦杆连续组合梁桥满足正常使用极限状态下的应力及刚度验算要求。钢管中的混凝土可以有效提高组合梁的弯曲刚度,降低组合梁的变形。
本文所提离散化的杆系建模方法便于进行波形钢腹板-多弦杆桥梁的构件验算。验算结果表明,该桥满足承载能力极限状态设计要求。

