基于径向基函数神经网络模型的桃江县森林碳储量估测

汪风华，文 敏，任蓝翔，胡中岳

(1.桃江县林业局，湖南 桃江 413400；2.国家林业和草原局中南调查规划设计院，湖南 长沙 410014)

碳储量是量化森林生态系统所需的重要变量之一。已有较多研究方法用于估测局部、区域以及全球范围的森林碳储量，比如野外测量、遥感方法和基于过程的生态系统模型等[1]。遥感技术的快速发展，为大面积、长周期的森林碳密度动态研究提供了新的途径和方法，遥感影像可以表征大面积土地表面特征。但是，由于光学和雷达影像的数据饱和，光谱和空间分辨率的限制，以及碳储量和光谱变量之间的复杂关系，使碳储量估测精度较低，尤其是当碳储量值过高或过低时[2]。

目前利用遥感估测森林碳密度，一般是通过遥感数据和森林地面样地建立数学模型实现不同空间尺度的估算[3]。常用方法中，经验模型简单、便于计算，但需要大量观测样点数据，受树种和区域背景影响较大[4]；过程模型能揭示碳储量的形成机理，但对观测数据要求较高[5]；半经验半物理模型简单直观，但缺乏植被生理机制方面的严密依据，很少用于森林碳储量的反演研究[6]；非参数估计模型忽略随机扰动项[7]，精度较高。本研究选取2013年桃江县森林资源一类调查数据和Landsat 8遥感影像，构建径向基函数(Radical Basis Function，RBF)神经网络模型，并与多元逐步回归模型(Linear Stepwise Regression，LSR)和偏最小二乘回归模型(Partial Least Square Regression，PLSR)进行对比，估测桃江县森林碳储量，探讨可以改善其过高和过低估计的建模方法。

1 研究区概况

桃江县位于湖南省益阳市，地处湘中偏北，资江下游，地理位置为111°36′—112°19′E，28°13′—28°41′N。该县国土总面积2068 km2，平均海拔200m，属亚热带季风气候，年均气温16.6 ℃，森林覆盖率62.98%，常见树种为杉木、马尾松、青冈等。

2 材料与方法

2.1 遥感影像及信息处理

研究选用2013年7月的Landsat 8 OLI 遥感影像，轨道号为124/040。用ENVI 5.3软件对其进行辐射校正和几何校正，误差小于半个像元。根据桃江县行政区划图对影像进行裁剪，得到桃江县Landsat 8遥感影像图。植被信息可以通过植被指数来表征。本研究选用Landsat 8影像多光谱波段以及6种植被指数及其衍生因子，作为碳储量遥感反演的可选光谱因子[8]，包括归一化植被指数(NDVI)、土壤修正植被指数(SAVII，I=0.1，0.25，0.3，0.5)、大气抗阻植被指数(ARVI)、增强型植被指数(EVI)、差值植被指数(DVI)、比值植被指数(RVI)，从而减少坡度和坡向的影响[9]。同时，用研究区DEM计算高程、坡向、坡度等地理因子，并提取3×3窗口下的纹理因子[10-11]。用ArcGIS 10.4软件获取变量因子值，用R软件corr.test()函数计算其与碳储量的相关系数。遥感变量作为模型的独立变量可能会彼此显著相关，导致信息重复并干扰模型性能。因此，需要对变量因子进行筛选。

2.2 样地信息获取与处理

研究以2013年桃江县一类调查数据为实测碳储量的数据来源。在桃江县的88个样地中，保留48个地类为林地的参与模型构建。目前对碳储量的估算主要根据生物量与含碳率的乘积，因此获取各树种生物量非常关键。竹林、灌木、经济林和混交林的含碳率均为0.5000，其他主要树种为：杉木0.5201，马尾松0.4596，硬阔叶类0.4834，软阔叶类0.4956，桉树0.5253[12]。

乔木林生物量采用李海奎等[12]2010年开创的模型(表1)，经济林和灌木林生物量分别为23.7 t·hm-2、19.76 t·hm-2，混交林按比例计。

2.3 多元逐步回归模型

多元逐步回归模型根据自变量因子是否同时符合两个条件来筛选：一是对因变量有足够影响力，二是因子之间相关性较低[13]。在不断的引入和删除自变量的过程中，既保证了多元逐步回归模型不会漏选对因变量影响显著的自变量因子，又可以避免多重共线性问题。

2.4 偏最小二乘回归模型

偏最小二乘回归模型可以从总体中筛选出具有最佳解释作用的综合自变量，可以解决变量之间的多重相关性[14]。首先计算交叉有效性和累计解释量，确定潜在建模因子个数，然后用投影重要性指标VIPj筛选出因子构建模型(式1)。

(1)

表1 乔木树种生物量计算方程Tab.1 Biomass regression equation and carbon content of different tree species树种生物量计算方程杉木和其他杉类BS=0.073 429(D2H)0.862 62;BP=0.013 775(D2H)0.844 63;BB=0.000 482(D2H)1.233 14; BL=0.019 638(D2H)0.789 69;BT=BS+BP+BB+BL马尾松和其他松类BT=0.071 556(D2H)0.857 209硬阔叶类软阔叶类BT=0.049 550 2(D2H)0.952 453BT=0.049 550 2(D2H)0.952 453桉树柏木BS=0.090 252 6D2.448 15; BB=0.004 916 3D2.817 79; BL=0.012 394D2.268 39; BT=BS+BB+BLBS=0.125 31(D2H)0.733; BB=0.137 403+0.012 887 D2H; BL=0.053 49+0.009 97D2H; BT=BS+BB+BL竹林BT=0.643 9D1.537 3 注:BS—树干生物量;Bp—树皮生物量;BB—树枝生物量;BL—树叶生物量;BT—地上部分总生物量;D—样地平均胸径;H—样地平均树高。

式中：n为自变量数，Ph为相关自变量主成分，R(Y，Ph)为因变量Y和相关自变量主成分Ph的相关系数，ωhj为自变量在主成分上的权重。

当VIPj值大于1，说明该自变量因子对因变量有强解释作用，对模型有重要贡献；当VIPj值小于1时，自变量的解释作用弱，对模型的贡献性小，VIPj<0.8的变量可以考虑剔除。

2.5 RBF神经网络模型

RBF神经网络模型可以有效避免局部极小问题，一般有三层：输入层、具有非线性激活功能的隐藏层和线性输出层[15]。本研究将通过K-means聚类得到的n个中心作为基函数的n个中心，隐藏层以高斯函数作为基函数，方差计算见式(2)，隐藏层到输出层的权重可以用最小均方根误差求得。该模型利用Matlab软件的newrb()函数来实现。

(2)

式中：σi为方差，cmax为聚类中心的最大距离，n为隐含层的节点数。

2.6 精度验证

将48个样地随机分成两部分：2/3(32个)作为训练数据，1/3(16个)作为验证数据，对3种模型得到的森林碳储量值开展精度验证。模型效果的评估选取决定系数R2和相对均方根误差RRMSE，计算公式分别见式(3)和式(4)。

(3)

(4)

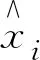
3 结果与分析

3.1 相关性分析

研究用ArcGIS 10.4软件提取Landsat 8的194个光谱、地理和纹理因子，作为建模可选的自变量因子，用R软件计算相关性(表2)。

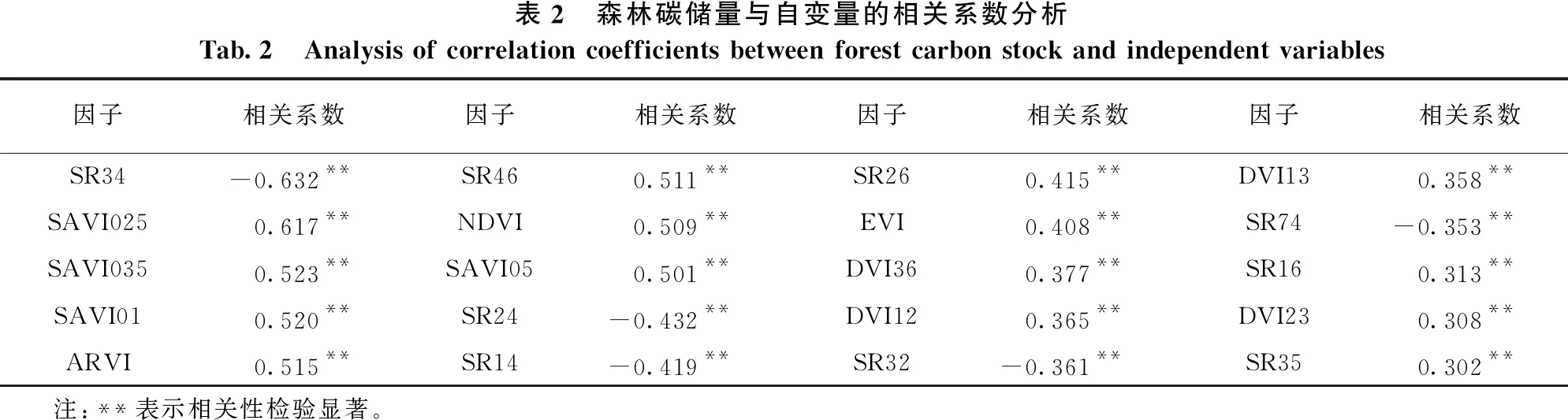
表2 森林碳储量与自变量的相关系数分析Tab.2 Analysis of correlation coefficients between forest carbon stock and independent variables因子相关系数因子相关系数因子相关系数因子相关系数SR34-0.632**SR460.511**SR260.415**DVI130.358**SAVI0250.617**NDVI0.509**EVI0.408**SR74-0.353**SAVI0350.523**SAVI050.501**DVI360.377**SR160.313**SAVI010.520**SR24-0.432**DVI120.365**DVI230.308**ARVI0.515**SR14-0.419**SR32-0.361**SR350.302** 注:**表示相关性检验显著。

由表2可知，有20个自变量因子在0.01水平与碳储量显著相关，其中SR34与碳储量的相关性最高，相关系数达到-0.632。光谱变量与碳储量的相关系数比碳储量与纹理因子和地理因子的相关系数高。

3.2 多元逐步回归模型

一般来说，拟合模型自变量越多，估测值的误差越小，模型性能越好。然而自变量增多会加大工作量，其中一些不显著因子会影响模型效果。因此，选择合适的自变量数目非常重要。研究用SPSS 22.0软件对样本数据进行标准化。由表3可知，经过4次拟合，4个自变量均进入了回归方程。随着自变量的增加，方程的决定系数R2随之增大，估计标准误差随之减小。当变量个数为4个时，R2达到0.608，校正R2达到0.607，模型效果较好。

因此，森林碳密度的最优回归方程包括SR34、SR46、NDVI、EVI共4个自变量，具体见式(5)。

y=-3.488+0.412x1+1.577x2+0.009x3-

1.707x4

(5)

式中：x1为SR34；x2为SR46；x3为NDVI；x4为EVI；y为碳储量。

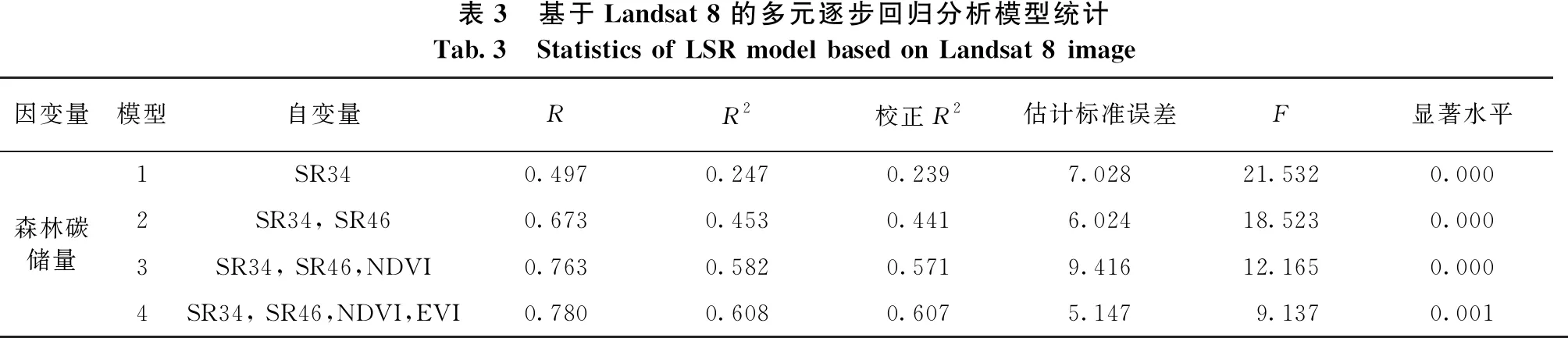
表3 基于Landsat 8的多元逐步回归分析模型统计Tab.3 Statistics of LSR model based on Landsat 8 image因变量模型自变量RR2校正R2估计标准误差F显著水平1SR340.4970.2470.2397.02821.5320.000 2SR34, SR460.6730.4530.4416.02418.5230.000 森林碳储量3SR34, SR46,NDVI0.7630.5820.5719.41612.1650.0004SR34, SR46,NDVI,EVI0.780 0.6080.6075.1479.1370.001

3.3 偏最小二乘回归模型

研究筛选20个显著相关的因子参与回归分析，设置潜在因子最大数为20，逐次分析随潜在因子量的增大自变量和因变量的累积解释量发生的变化，选取最优偏最小二乘模型。累积解释量随潜在因子数量变化过程如图1所示。

由图1可知，使用20个自变量参与建模，当潜在因子数量不同时，累积解释量也会发生变化。大于8个时，自变量累积解释量增长幅度趋于平缓，因变量累积解释量则出现下降趋势。说明PLSR分析的最佳潜在因子数量为8个。计算20个自变量因子的投影重要性指标，结果见图2。

由图2可知，有6个自变量因子的VIP值大于1，说明对模型的贡献性强；2个因子VIP值小于1而被剔除。排在前8位的自变量因子依次为SR34、DVI12、NDVI、SR32、SAVI025、ARVI、SAVI01、SR46，偏最小二乘回归模型见式(6)。

y=5.162+0.097x1+0.677x2+0.007x3+

0.635x4-0.501x5-1.213x6-0.412x7-

0.144x8

(6)

式中：x1为SR34；x2为SR46；x3为NDVI；x4为SR32;x5为SAVI025;x6为 ARVI;x7为SAVI01;x8为DVI12；y为碳储量。

3.4 RBF神经网络

将2/3的样本(32个)作为训练数据，筛选出显著相关的变量20个，组成32×20的矩阵作为输入向量，碳储量作为输出向量。调用Matlab软件中的newrb函数创建神经网络，均方根误差为0.001，最大神经元个数为200，创建函数分布密度为0.1、0.2、0.3、0.4、0.5的5个神经网络模型，当分布密度为0.1时，拟合效果最好。此时模型拟合的决定系数达到0.633，相对均方根误差为15.250 t·hm-2，效果较好。

3.5 模型比较

以剩下的1/3样本(16个)对3种方法得到的森林碳储量值进行精度验证，分别计算R2和RRMSE，结果如表4所示。

由表4可知，RBF神经网络模型预测精度最高，R2达到0.645，RRMSE为15.582 t·hm-2；其次偏最小二乘回归模型(PLSR)；多元逐步回归模型(LSR)精度最低。在本研究区，神经网络模型在估测碳储量时表现较好。

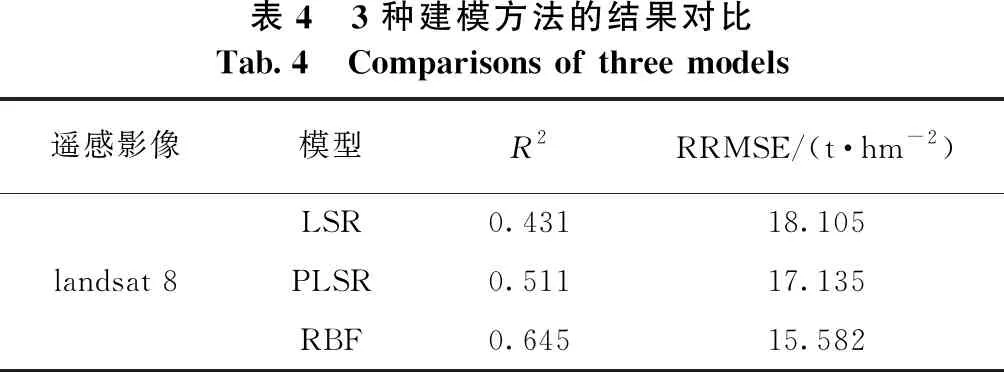
表4 3种建模方法的结果对比Tab.4 Comparisons of three models遥感影像模型R2RRMSE/(t·hm-2)LSR0.43118.105landsat 8PLSR0.51117.135RBF0.64515.582

3.6 桃江县森林碳储量空间分布

根据RBF神经网络模型绘制了桃江县碳储量空间分布图(图3)。由图3可知，桃江县海拔较高的地方碳储量较大，分布在30～60 t·hm-2范围内；城区碳储量较低，分布在0～30 t·hm-2范围内。

4 结论与讨论

结合Landsat 8影像和2013年桃江县一类调查数据，建立多元逐步回归、偏最小二乘回归和RBF神经网络模型，反演桃江县碳储量。

(1)利用遥感影像原始波段计算的植被指数与森林碳储量相关性较高，可以准确高效地预测森林碳储量。

(2)RBF神经网络模型效果最好，决定系数和相对均方根误差分别为0.645和15.582t·hm-2；其次是偏最小二乘回归模型，分别是0.511和17.135 t·hm-2。多元逐步回归模型估算精度最低，分别为0.431和18.105 t·hm-2。

(3)高海拔地区碳储量大，城市地区碳储量较小，符合桃江县植被覆盖实际情况。

与现有研究[16-18]相比，本研究引入RBF神经网络优于传统经验模型，拟合精度高，估计误差小，无局部极小问题存在，且学习过程收敛速度快。但仍存在一些不足，比如参数选定较为困难，不能很好的解释推理过程和推理依据。下一步研究重点将集中在优化模型参数选取。