微纳聚合体卫星的对称式重构规划算法

康国华，刘奇弦，吴佳奇，王 强

(南京航空航天大学航天学院，南京 210016)

0 引 言

微纳聚合体卫星是由多个立方体微纳卫星通过组合机构而形成的动态组合体航天器。通过以磁力铰链为组合机构进行研究，铰链分布于每个卫星的12条棱上，微纳卫星在磁力铰链的约束下以棱为转轴进行转动，从而实现微纳聚合体卫星的构型重构。图1为磁铰链布局和变构过程原理示意图。

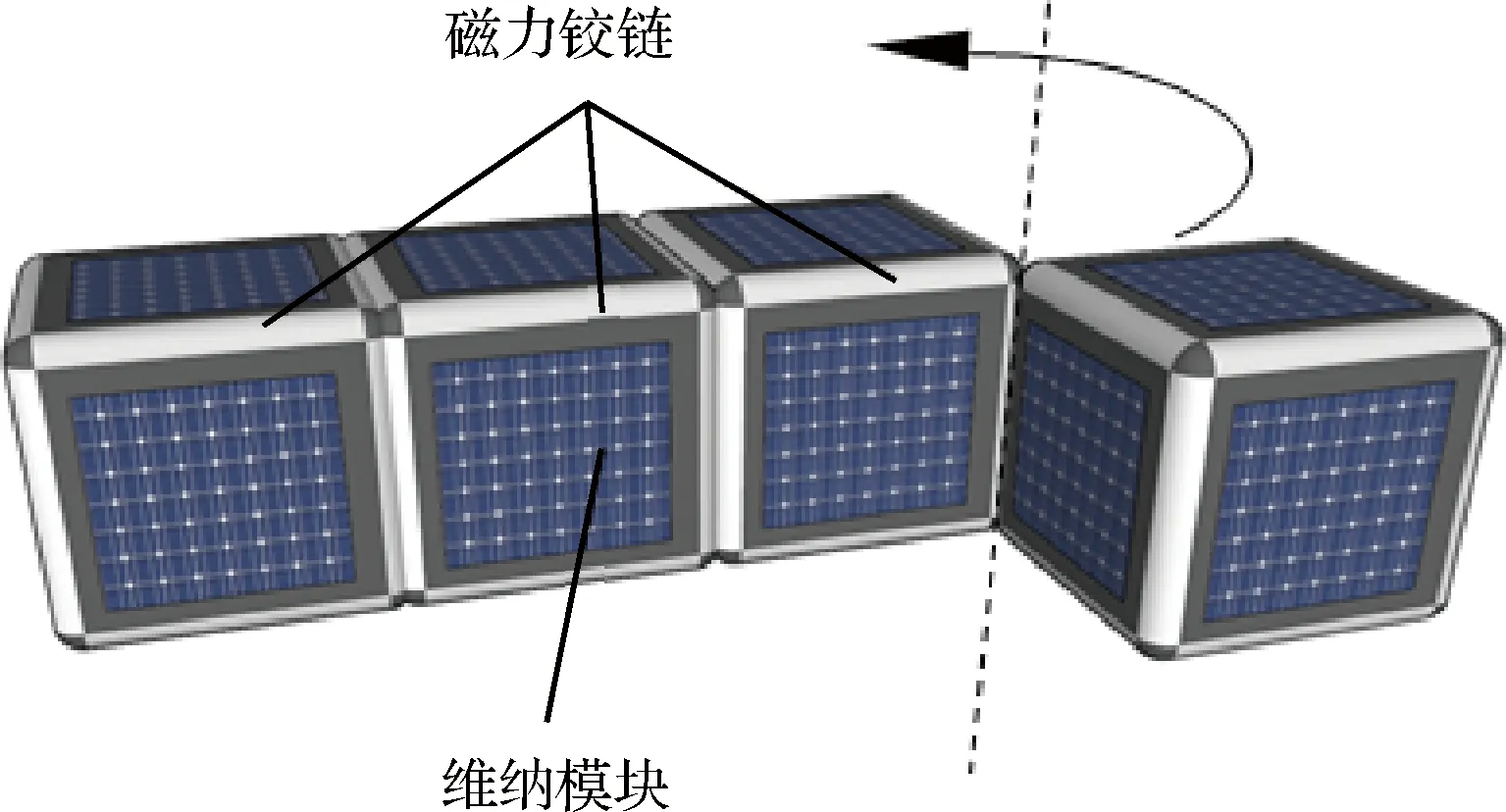
图1 微纳聚合体卫星变构原理Fig.1 Principle of reconfiguration of CBMS

构型可重构的模块化航天器由于具有较强的可扩展性、较强的适应性，可满足不同的任务需求，近年来引起了各国研究人员的关注。日本开展了板块延展卫星(Panel extension satellite, PETSAT)计划[1-2]，但卫星面板之间通过机械铰链连接，连接方式在地面确定，无法在轨更改，因而无法实现任意形态的重构。英国萨里大学的可重构太空望远镜自主拼接(Autonomous assembly of a reconfigurable space telescope, AAReST)项目，计划通过多颗卫星模块的分离与再拼接实现不同望远镜构型之间的变换，以满足不同的成像需求[3-4]。但分离后再拼接的策略在控制上面临姿轨耦合问题的挑战，姿轨耦合控制也会导致额外的燃料消耗。

磁力铰链的示意图如图2所示，基于磁力铰链的微纳聚合体卫星利用了铰链约束的特性，可将微纳模块的转动转化为位置的改变，磁力铰链分布于微纳模块的12条棱上，通过电流的通断决定铰链的吸附与分离，这使得微纳模块可实现在三个方向的转动。这意味着通过不同模块的多次运动可实现任意两构型之间的变换。对于磁铰链连接机构的研究主要集中在模块化机器人领域，美国麻省理工学院提出了M-Blocks[5]可重构模块化机器人，立方体模块通过绕分布于各棱的磁铰链转动实现形态的重构，该机构相比于机械连接机构，对模块相对位置关系宽容度更高，但该型机器人工作于地面环境。目前磁铰链在航天器上的应用较少，有待进一步研究。

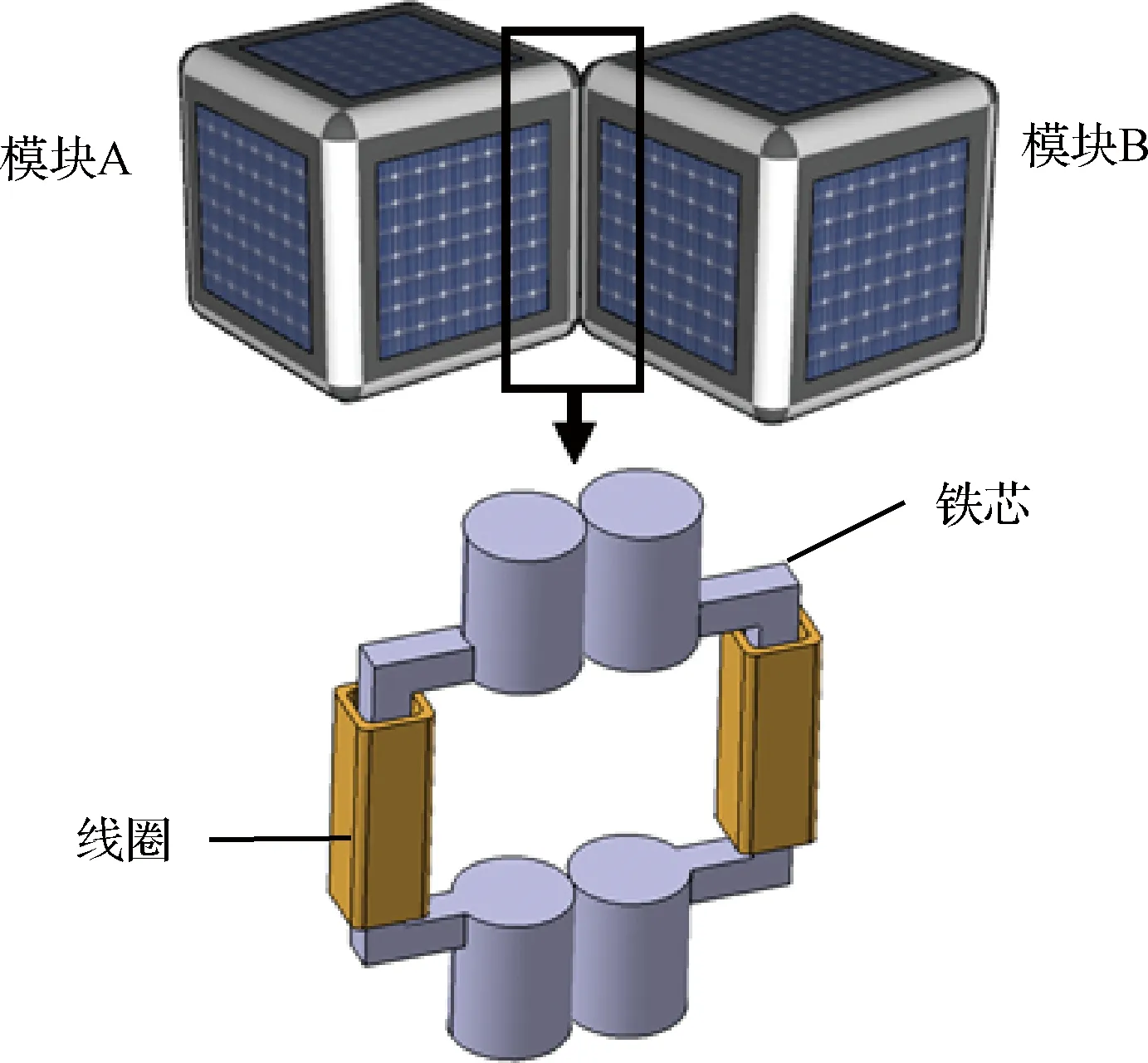
图2 磁力铰链示意图Fig.2 Schematic diagram of magnetic hinge

微纳聚合体卫星是一个漂浮基多刚体系统，系统中每两个通过磁铰链连接的刚体之间动力学是耦合的，铰链处内力会导致一对力矩作用于铰链两侧的刚体，从而影响两者的姿态。多刚体系统的建模方法有经典力学方法、Kane法、R-W方法等。以牛顿-欧拉方程为代表的经典力学法将系统中的刚体分割为独立刚体，刚体间内力视为外力施加于各刚体，该方法随刚体数增加，方程数也增加，求解难度大大增加[6-8]。Kane法用广义速率描述系统运动[9]，计算量比经典力学的方法少，但该方法不适用于任意多刚体系统，需对研究对象具体分析。Roberson和Wittenburg[10]将图论引入多刚体动力学，提出了R-W方法，用有向图描述系统构型，可用于任意结构的多刚体系统，适用于对微纳聚合体卫星进行建模。

可重构系统的重构规划的目的是使该系统能在尽可能满足最优指标(如最少步数)的情况下实现构型的转换。林晓青等[11]利用遗传算法设计了检测机器人群组的站位规划策略。Rus等[12]提出了Melt-Grow算法，可用于立方体形状的模块化机器人的重构，他将目标构型分解为链状的中间构型，目标构型由中间构型形成。但上述研究的对象为模块化机器人或机器人群组，未考虑航天器动力学特性，需设计一种适用于模块化航天器的规划算法，能有效减小各模块的运动对航天器姿态的影响。

本文利用R-W法对微纳聚合体卫星进行动力学建模，分析了重构过程中的动力学耦合特点，提出了一种对称式重构规划算法，以减小重构过程中各模块的运动对航天器姿态的影响。

1 动力学分析

1.1 动力学模型的建立

微纳聚合体卫星重构时，可分为两个部分：1)若干模块通过锁紧机构锁紧而形成的组合体，该组合体可看作单个刚体，以下称为本体；2)与本体解除锁定，在磁力铰链的约束下发生转动的模块，以下称为运动模块。微纳聚合体卫星由一个本体与多个运动模块组成。由于微纳聚合体卫星为漂浮基多刚体系统，故引入一虚拟刚体与一虚拟球铰链，本体通过该虚拟球铰与虚拟刚体相连，虚拟刚体姿态不变，质量为0。以运动模块数为3的系统为例进行分析，该系统如图3所示。

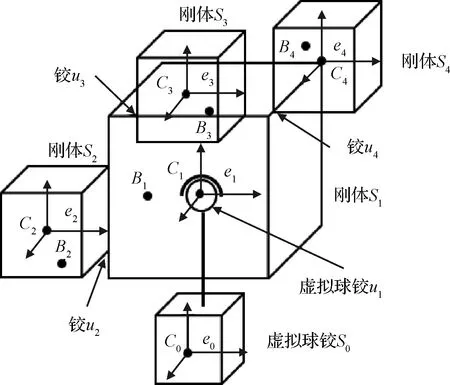
图3 多刚体系统示意图Fig.3 Schematic diagram of the multi-rigid-body system

本体虽形状不规则，但可等效为质量、惯量、质心位置相同的长方体。刚体S1，S2，S3，S4分别为运动模块，e0到e4分别为固连于各刚体的基，C0到C4分别为各刚体质心。

为建立动力学方程，引入增广体的概念。对于刚体Si，在其与其他刚体相连的铰链中心处附加一质量点，该点质量为直接或间接通过该铰链与刚体Si相连的其他刚体质量之和，则形成的新刚体为增广体。Bi为Si对应的增广体质心。

该系统的拓扑结构如图4所示，该系统为一树形多刚体系统。

图4 多刚体系统拓扑结构Fig.4 Topology of the multi-rigid-body system

用关联矩阵S与通路矩阵T描述该系统结构，两矩阵的定义如下：

(1)

i=0,…,4,j=1,…,4

(2)

i,j=1,…,4

对于图4所示拓扑结构，关联矩阵与通路矩阵的值分别如下：

取φ=[φ11,φ12,φ13,φ2,φ3,φ4]T为广义坐标，其中φ11到φ13分别为刚体S1绕铰u1转动的欧拉角，φ2到φ4分别为刚体S2到S4绕铰u2到u4转动的角度。则根据R-W方法列出如下的动力学方程：

(3)

f=w+w*

(4)

(5)

(6)

(7)

[ωj×(ωj×bji)]，i=1,…,4

(8)

将刚体S1的转动分解为三次连续的转动，则p1j(j=1,2,3)为三次转动的转轴方向上的单位矢量(在基e0中表示)，pi(i=2,3,4)为刚体Si转轴方向上的单位矢量(在基e1中表示)。

对于其他构型的系统，动力学建模过程仍与此类似。

1.2 对称式重构过程的动力学分析

运动模块转动过程中，铰链处的内力对于微纳聚合体本体来说为外力，该力会产生力矩以影响本体的姿态。当多个运动模块同时运动时，有多个力矩同时施加于本体。很明显，如果其中一对力矩大小相等、方向相反时，两者对本体姿态的影响可相互抵消。经分析，当两个运动模块的位置、转动方向等满足：运动模块转轴相互平行，转动方向相反，自身质心与本体质心距离相等的条件，即可实现力矩的抵消。上述条件在本文中定义为对称性条件。

如图5所示，当模块A和模板B围绕z轴转动、方向相反时即满足对称性条件。两模块质心坐标分别为(x1,y1,z1)和(x2,y2,z2)，本体质心坐标为(xc,yc,0)，两模块与本体相连的铰链中心点与本体质心的距离分别为L1和L2。当L1=L2且z1=-z2时，铰链处内力产生的合力矩最多只有两个自由度，即最多对本体姿态产生两个自由度的影响。当z1=z2=0时，合力矩为0，对本体姿态的影响可完全抵消。

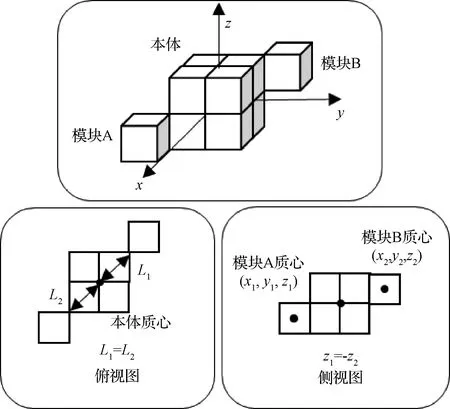
图5 对称性条件Fig.5 Symmetry condition

为分别对:1)z1=-z2且z1≠0，z2≠0; 2)z1=z2=0两类对称式重构情形进行仿真分析，分别设定如图6(a)和(b)所示的两个仿真场景。

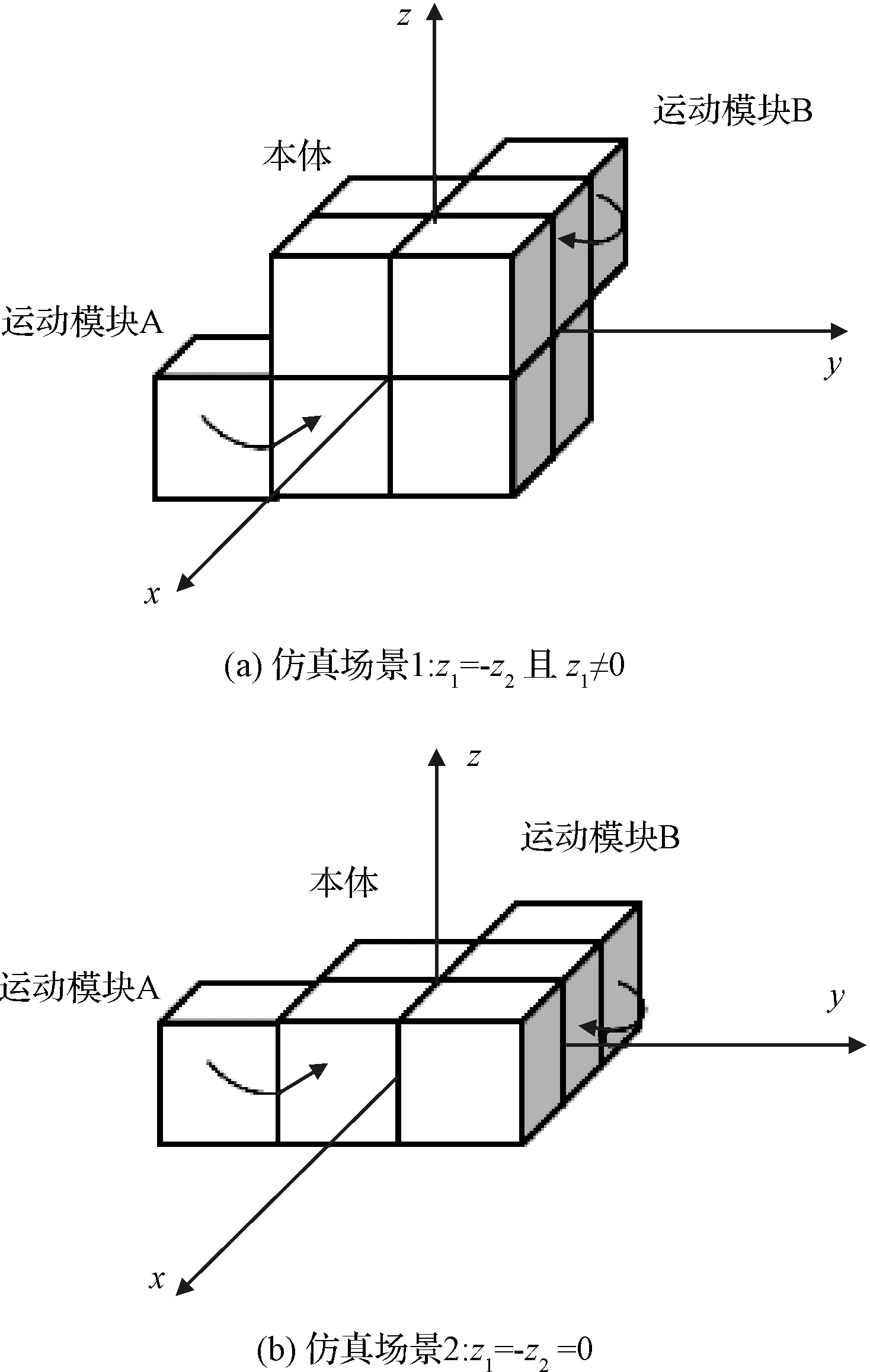
图6 动力学仿真场景Fig.8 Dynamic simulation scene

图6中各运动模块在0.01 N·m的恒定力矩作用下转动。假定理想情况下，力矩同时作用于不同运动模块，各模块质心位于形心，各模块标称质量均为10 kg，模块各主轴标称惯量均为0.2 kg·m2，标称棱长均为0.3 m，初始姿态与角速度均为0。

然而工程实现中，各模块的尺寸、质量、惯量以及模块运动开始时间等参数可能不完全相同，这些参数的不一致性可能会对对称式重构过程中本体姿态带来额外的影响。下文在考虑以上参数不一致性的情况下对变构过程本体姿态变化进行仿真分析。

由于仅研究不同模块间的相对差异，不考虑模块参数的绝对误差，因此为各模块的尺寸、质量、惯量等参数附加均值为0，标准差不为0的随机偏差。

模块尺寸的不同带来的影响主要体现在质心位置的不同。目前质心测量相对误差已低至0.1%量级[13]，因此给各模块质心坐标引入均值为0，标准差为0.005 m的随机偏移量。各模块质量、惯量仍相同，质量仍为10 kg，各主轴惯量仍均为0.2 kg·m2，模块在0.01 的恒定力矩作用下同时转动。分别对图6(a)和(b)所示的场景1与场景2进行动力学仿真，得到本体姿态角变化曲线分别如图7(a)和(b)所示。

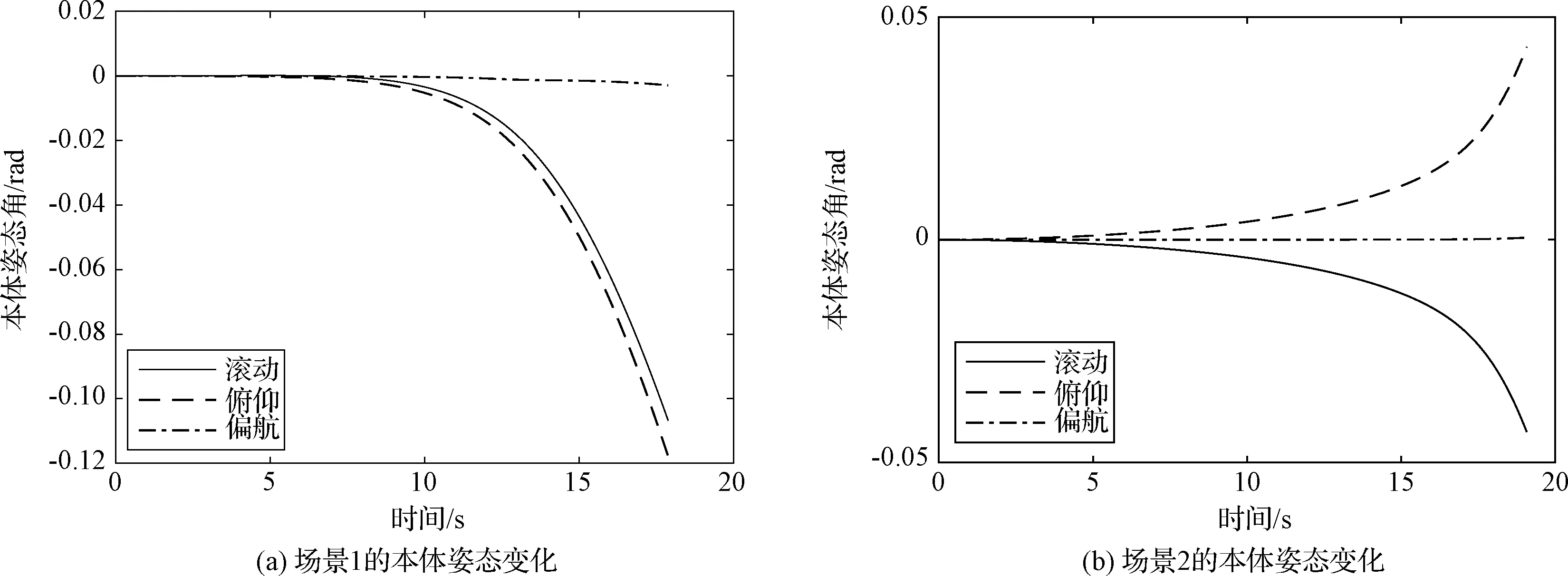
图7 考虑模块质心位置差异的本体姿态变化Fig.7 Change of attitude of the mainbody considering the difference of centroid position between modules

由图7(a)和(b)可知，考虑可模块质心位置差异后，场景1、2本体姿态变化仅在10-2rad量级，场景一稍大，且两类对称式重构能保证本体至少有一个自由度的姿态保持稳定。

目前质量测量相对误差已低至0.1%量级[14]，因此，为研究模块质量的不一致性带来的影响，各模块在10 kg标称质量基础上引入均值为0，标准差为0.1 kg的随机质量偏差，其他参数为标称值。分别对图6(a)和(b)所示的场景1与场景2进行动力学仿真，得到本体姿态角变化曲线分别如图8(a)和(b)所示。

图8 考虑模块质量差异的本体姿态变化Fig.8 Change of attitude of the mainbody considering the difference of mass between modules

由图8(a)和(b)可知，考虑模块质量差异后，场景1本体姿态变化仅在10-2rad量级，场景2仅在10-3量级，其中，场景2中本体滚动与俯仰角均保持稳定。

目前惯量测量相对误差已低至0.01%量级[14]，因此为研究模块惯量差异的影响，各模块在0.2 kg·m2的标称惯量基础上引入均值为0，标准差为0.001 kg·m2的随机惯量偏差，其他参数为标称值。仍分别对图6(a)和(b)所示的场景1与场景2进行动力学仿真，得到本体姿态角变化曲线分别如图9(a)和(b)所示。

由图9(a)和(b)可知，考虑模块惯量差异后，场景1本体姿态变化仅在10-2rad量级，场景2仅在10-4量级，其中，场景二中本体滚动与俯仰角均保持稳定。

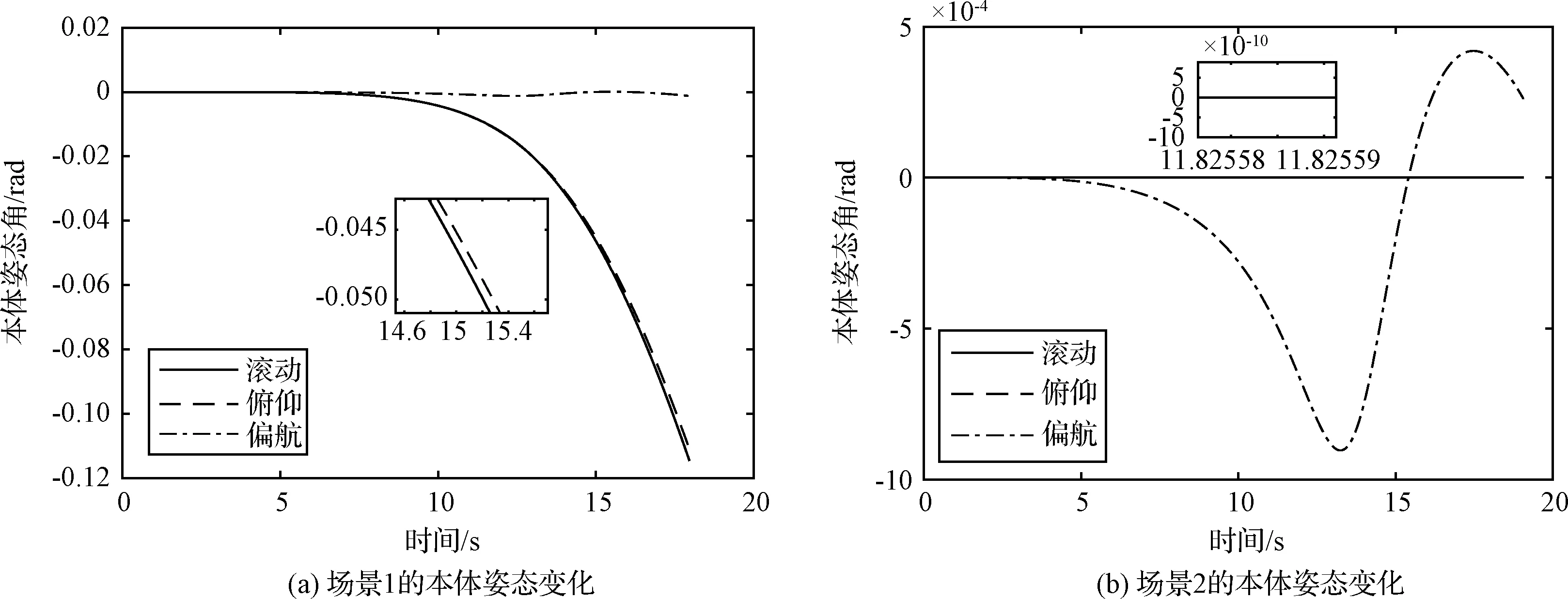
图9 考虑模块惯量差异的本体姿态变化Fig.9 Change of attitude of the mainbody considering the difference of inertia between modules

为研究模块运动开始时间的差异对对称式重构中本体姿态的影响，使图6(a)和(b)所示的场景1与场景2中运动模块B相对于运动模块A延迟0.5 s开始运动，得到本体姿态角变化曲线分别如图10(a)和(b)所示。

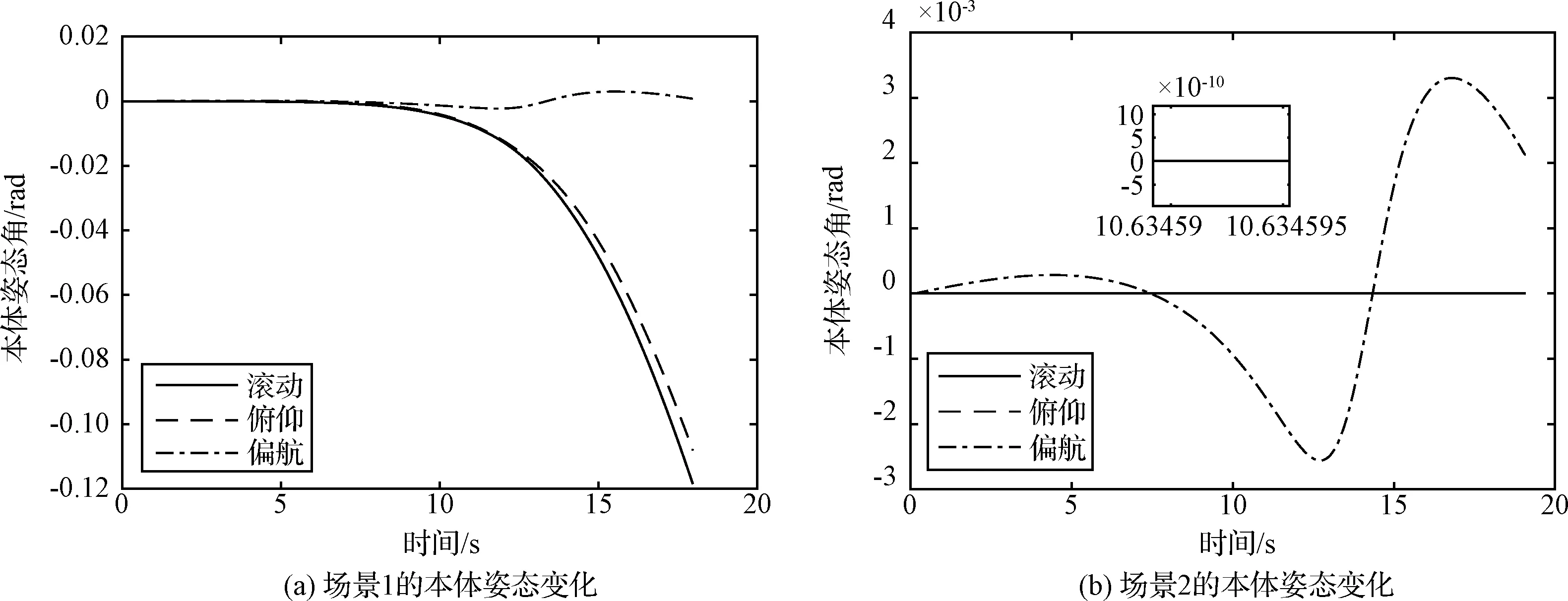
图10 考虑模块运动开始时间差异的本体姿态变化Fig.10 Change of attitude of the mainbody considering the difference of start time of movement between modules

由图10(a)和(b)可知,考虑模块运动开始时间差异后，场景1本体姿态变化仅在10-2rad量级，场景2仅在10-3量级，其中，场景2中本体滚动与俯仰角均保持稳定。

为进一步验证对称式重构的有效性，对不满足对称性条件的非对称式重构过程进行动力学仿真，仿真场景如图11所示，除重构运动方式和组合体构型不同外，其余参数设置均与上述仿真相同。

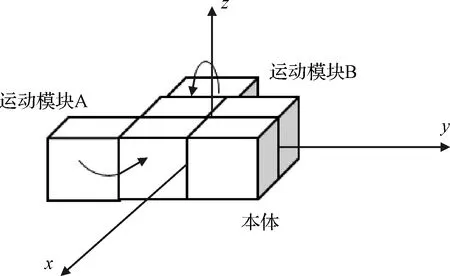
图11 动力学仿真场景Fig.11 Dynamic simulation scene

仿真得到的本体姿态变化曲线如图12所示。

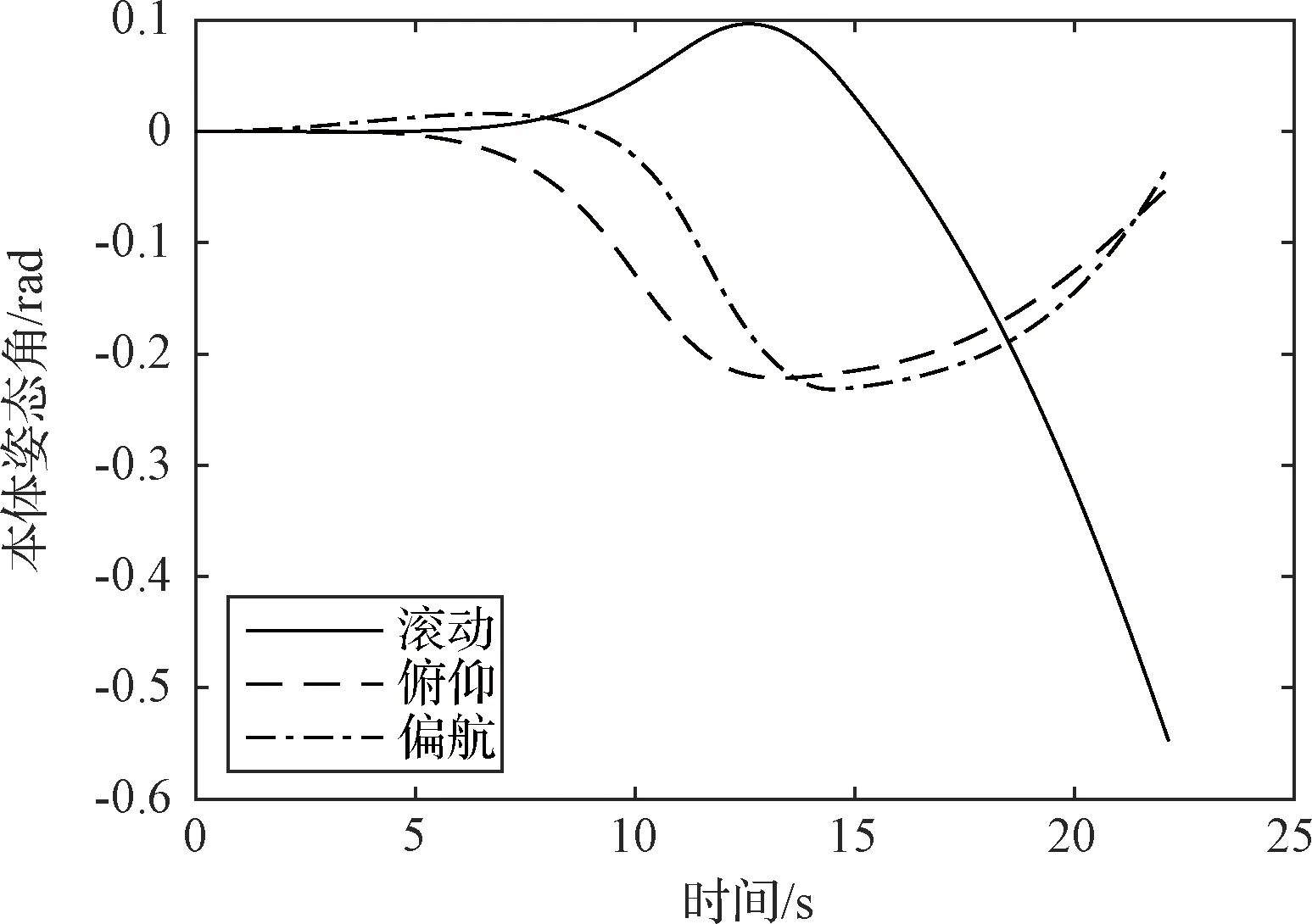
图12 非对称式重构下本体姿态变化曲线Fig.12 Change of attitude of the mainbody under asymmetric reconfiguraton

由图12可知，非对称式重构下，本体姿态相比于对称式重构发生了更大的变化，其中滚动角的变化超过了0.5 rad，说明非对称式重构对本体姿态有较大冲击，而对称式变构可避免这一问题综合分析上述仿真结果，可知考虑了不同模块质心位姿、质量、惯量、运动开始时间的差异的情况下，对称式变构仍能保证本体至少一个自由度的姿态稳定，其他轴向的姿态变化幅度也较小。由此证明，对称式重构在各模块质心位置、质量、惯量、运动开始时间存在一定差异的情况下仍能在一定程度上减小本体姿态所受的影响。

2 重构规划算法设计

2.1 构型的表示方法及其合理性判定

利用三维空间网格表示各模块的位置[15]，则各模块位置对应一个整数坐标，则组合体构型可用一个三维整数坐标的集合表示。一个集合中的所有点进行相同的旋转、平移变换后所得到的新集合与原集合表示的构型为同一构型。

并非任意集合都可表示组合体构型，当集合中出现如图13中(2)(3)所示两种结构时，认为该集合不合理，在重构过程中应排除。

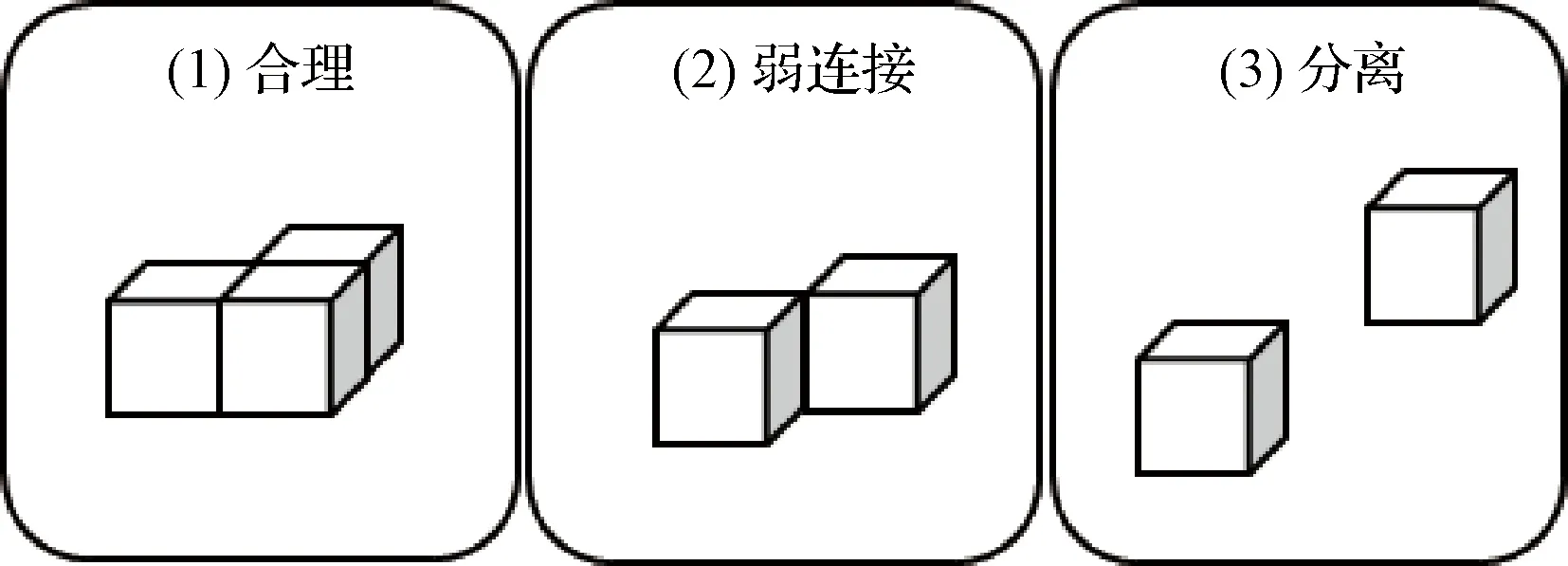
图13 合理与不合理构型的示例Fig.13 Examples of reasonable and unreasonable configurations

文中将模块面接触定义为连通，分离和弱连接定义为非连通。此外构型的连通性可通过求解无向图中各节点间最短路径的方法判断。

判断流程如图14所示，将构型中每个模块作为无向图中的顶点，当某模块的某面与另一模块的某面相接触时，则认为两模块相连，在无向图中对应两顶点通过一条边相连，所有相连顶点之间的边的权值均为1。得到无向图之后，计算该无向图中所有顶点与其他顶点间的最短距离(两顶点间最短通路上的权值之和)，若存在某两顶点间的距离为无穷大，则该构型不连通。

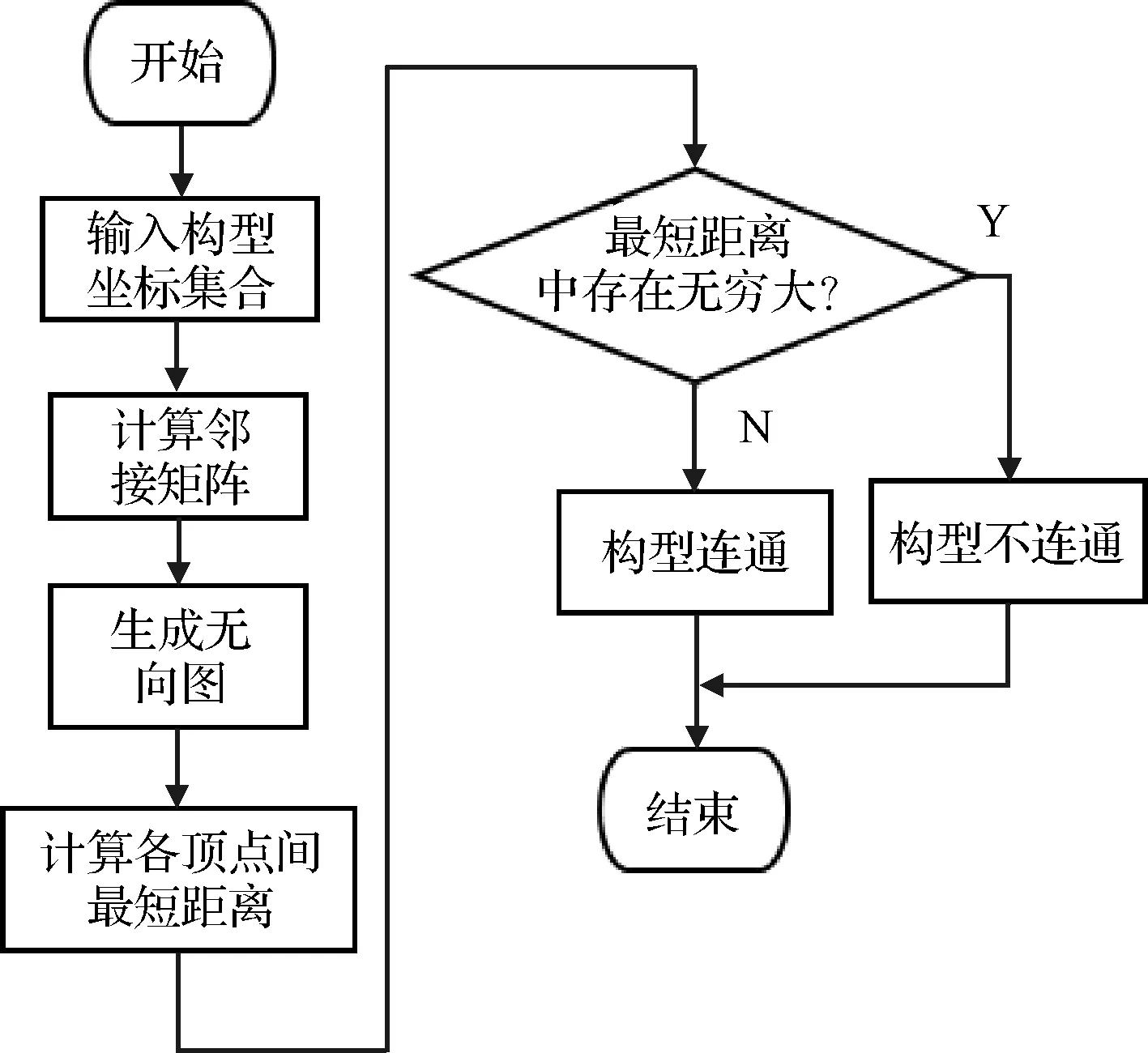
图14 构型连通性判断流程Fig.14 Program flow to judge connectivity of configurations

2.2 不同构型间差异度的评价指标

微纳聚合体卫星从初始构型变换为目标构型的过程可类比为路径规划的过程，重构过程中每一个中间构型相当于路径上某一节点。要以尽可能少的步数实现重构，相当于寻找从初始构型到目标构型间的最短路径。最主要的问题是找到一个指标，可以衡量两构型间的“距离”，重合度以及最优分配度量[16]均可实现以上功能。

重合度可用两构型对应的坐标集合的交集的元素个数来衡量。构型A对应的模块坐标集合为α，构型B对应的模块坐标集合为β，两集合交集为γ=α∩β，则集合γ中元素的数量为两构型的重合度。

最优分配度量的计算方法如下文所述。

ai(i=1,…,n)为构型A中的模块，bj(j=1,…,n)为构型B中的模块，定义如下函数：

f(A,B)=∑1≤i, j≤nkijdij

(10)

式中：dij为ai到bj的网格距离(即在网格中移动的最小步数)，当ai将移动到bj位置时，kij为1，否则为0。由于各模块初末位置一一对应，因此有以下约束：

(11)

(12)

定义最优分配度量为：

δ(A,B)=minf(A,B)

(13)

则最优分配度量值可由Hungarian算法[17]求得，求解过程由以下示例进行说明。

图15(a)为当前4个模块组成的平面构型，(b)为目标构型，(c)为两构型的叠加。由于各模块位置确定，因此叠加构型唯一确定。

图15 示例构型Fig.15 Example of configurations

定义4×4的矩阵D，其元素Dij=dij(图15(c)中模块i到j’的网格距离)。则矩阵D的值如下所示：

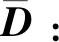
δ(A,B)=D11+D22+D33+D44

(14)

2.3 重构规划算法设计

重构规划算法需要找到一条从初始构型到目标构型的较短的“路径”，对路径的搜索方法以A*算法为基础，将最优分配度量与重合度共同作为“路径”上节点之间距离的度量指标，为达到对称式重构的目的，根据1.2中构型变化对称性判定条件对中间构型进行筛选。

根据A*算法的原理，定义估价函数f(x)=d(x)+h(x)，其中d(x)为初始构型到当前构型x的变换步数，h(x)为当前构型x到目标构型的估计距离(与最优分配度量值呈正相关，与重合度呈负相关)。搜索前建立open列表与close列表；将初始构型作为当前的父节点构型，将初始构型存入close列表；根据模块运动约束得到父节点构型所有可达构型，并将不在close列表中的可达构型放入open列表；用对称性条件考察open列表中的构型，若存在满足条件的构型，则将不满足条件的构型从open列表删除；在open列表中筛选出与目标构型重合度度量值最大的构型，其余构型从open列表中删除；在open列表中筛选出与目标构型最优分配度量值最小的构型，其余构型从open列表中删除；随机选择open列表中剩余构型之一，将其作为新的父节点构型，并存入close列表；重复以上步骤，直到目标构型出现在open列表中。算法流程如图16所示。

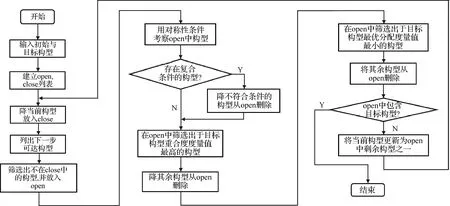
图16 重构规划算法流程Fig.16 Program flow of reconfiguration planning

3 算法校验

微纳聚合体卫星的一种典型应用场景为空间阵列天线的展开与构型变换。其构型分为发射构型(即由运载火箭发射时的小包络尺寸构型)和在轨构型(即入轨后根据不同功能需求展开而成的构型)。在轨构型中，阵列天线常用的典型构型包括面阵构型与线阵构型。本节采用对称性重构规划算法对以上三类典型构型间的变换进行校验。

1)发射构型重构为面阵构型

模块总数为12，需以适当比例设置运动模块数量。考虑到运动模块数量不宜过多，为在运动模块数量较少的情况下校验算法对对称运动的筛选作用，本算例将运动模块数量上限设置为仅大于1的奇数3，规划结果如图17所示。

图17 算例1计算结果Fig.17 Calculation result of numerical example 1

2)发射构型重构为线阵构型

参数设置与(1)相同，规划结果如图18所示。

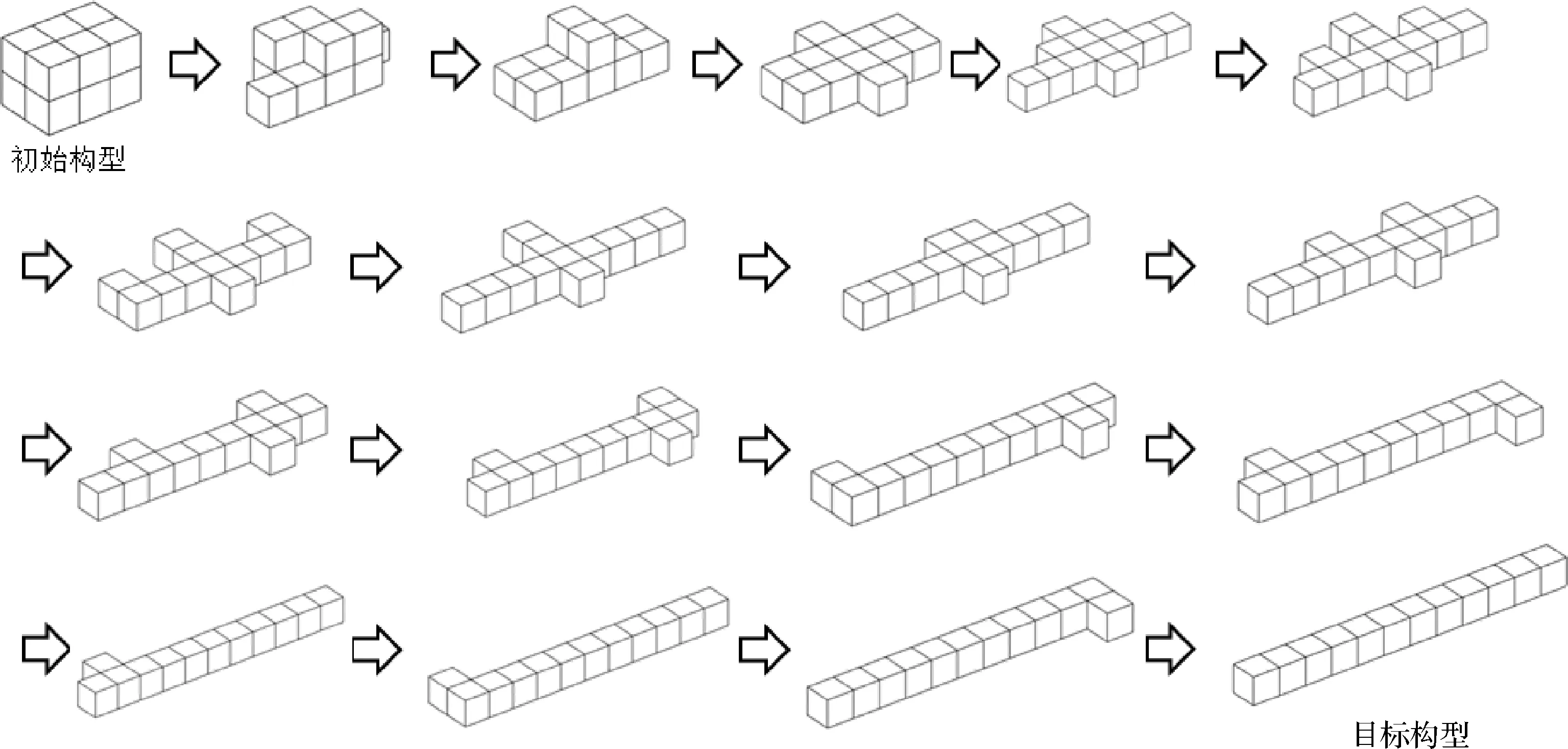
图18 算例2计算结果Fig.18 Calculation result of numerical example 2

3)面阵构型重构为线阵构型

参数设置与(1)相同，规划结果如图19所示。

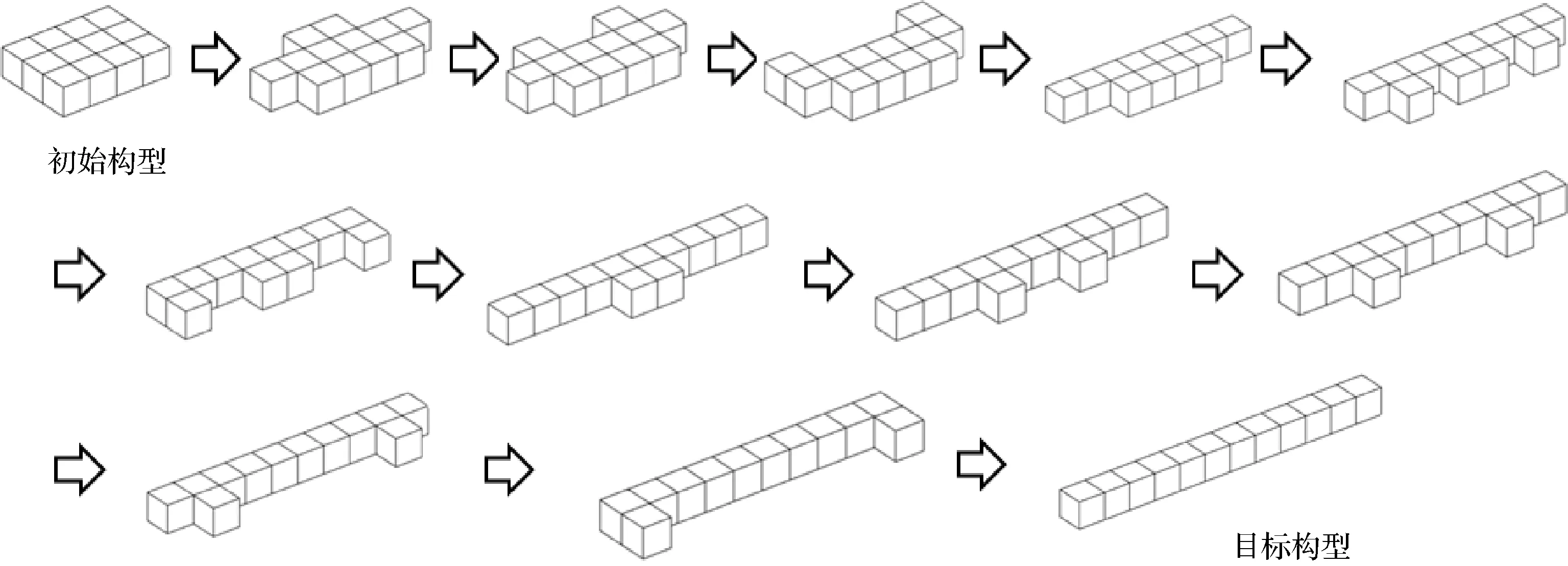
图19 算例3计算结果Fig.19 Calculation result of numerical example 3

3个算例由规划算法得到的重构过程总步数、对称式重构步数及其所占的比例如表1所示。

表1 规划计算结果分析Table 1 Analysis of calculation result of planning algorithm

由表可知，对于三个算例，组合体都在较少的步数内完成了重构。其中对称式重构的步数所占的比例在不同算例中差别较大，但最低也接近50%，最高为100%，证明了对称式重构规划算法的有效性。

4 结 论

本文为解决微纳聚合体卫星的重构规划问题，首先建立了动力学模型，对其进行动力学分析。仿真结果表明：当某两个模块的运动满足对称性条件时，两者的运动对微纳聚合体卫星本体姿态的干扰可相互抵消。

基于上述分析，本文设计了微纳聚合体卫星对称式重构规划算法。通过3个典型算例对该算法进行校验。校验结果表明：该算法可实现在尽可能多的对称运动步数下进行重构。

同时，由仿真结果可知，不同的初始与目标构型下，对称运动比例差别较大，说明算法运行结果对各初始条件敏感。因此，初始与目标构型、模块总数、运动模块数量等因素对规划结果的影响有待研究。此外，对称性步数是否存在理论上限，是否存在无法对称变构的构型等问题有待进一步研究。