火星探测天线组阵数据接收技术研究和验证实验
孔德庆,李春来,张洪波,苏 彦,刘建军,徐茂格,朱新颖,李俊铎,薛喜平
(1. 中国科学院国家天文台,中国科学院月球与深空探测重点实验室,北京 100012;2. 中国西南电子技术研究所,成都 610036)
0 引 言
随着深空探测与射电天文的迅猛发展,对射电望远镜的性能提出了新的需求[1-3]。然而,目前由于大口径天线和低噪声接收机等存在工程极限,单个天线性能的提高已经到了停滞状态,通过大量小天线组阵的方法是获得更高天线性能的基本途径。天线组阵技术除了能够实现等效口径大天线接收能力的同时,还具有更大的视场、更高的系统可靠性、更低的建造维护费用、更好的计划灵活性和对射电天文科学研究更广泛的支持。天线组阵技术已成为深空通信和射电天文技术发展的主要方向[4]。
美国深空网早在20世纪70年代就开始进行天线组阵技术的研究和深空探测任务的执行,最初利用已有的深空通信大天线和大型射电天文望远镜组阵。先后分别建成了三套全频谱组阵系统[2,5],在几乎每次的深空探测中都进行了天线组阵的数据接收。分别利用深空站的34 m、64 m、70 m天线以及射电天文的Parkes 64 m天线、VLA 27面25 m天线阵等,在水手号、Voyager、Galileo、Cassini和先驱者号等系列深空探测器,在探测水星、木星、土星、天王星和海王星等任务中,都利用天线组阵技术进行了下行科学数据的接收,成功实现了深空探测器科学数据的最大效率回传[6]。目前,正在建设和计划建设的天线阵主要有SKA(平方公里阵)[7]、阿伦望远镜[2]、DSN(美国深空网)大型阵等。NASA已明确表示在未来的深空探测中,将不再建设大型单口径天线,而是采用中小天线组阵的方式[2],DSN大型阵就是针对未来的深空探测,用于替换目前的70 m天线而研制的新一代天线阵。DSN大型阵采用数百个直径为6~15 m的小天线进行组阵,它将从总口径为2倍70 m天线口径的原型系统开始,在资金许可的条件下可以做成原型的100倍;不过,目前这一系统面临着微弱信号相关与合成的问题[8]。国内除了中科院国家天文台、上海天文台已建成或正在建设的用于射电天文观测研究的天线阵外,我国用于执行深空探测数据接收任务的天线组阵仍停留在实验阶段。分别在国家天文台密云站建立了4天线Ku频段实验系统[9],在北京怀柔建立了4天线S/X频段实验系统,并针对嫦娥2号、同步卫星等进行了组阵实验[10],舒逢春等[11]利用VLBI数据进行了组阵实验。
我国首次火星探测任务已经立项,根据我国的深空探测规划,后续还将进行多次月球、火星、木星及远至太阳系边缘的行星际穿越的深空探测。地面接收到的探测器信号非常微弱,如采用现有的单天线接收,无法满足探测器的科学数据下行需求。为了确保探测器有效载荷科学数据的顺利下传,在首次火星探测任务中拟采用密云站GRAS-1天线(口径50 m)、昆明站GRAS-2天线(口径40 m)、密云站GRAS-3天线(口径40 m)和正在建设中的武清站GRAS-4天线(口径70 m)组阵接收的方案来满足数据接收的需求。4面天线组成的天线阵等效口径可达102 m,针对后续更远的深空探测任务,根据需要也可将国内其他大型天线,如上海天文台天马站65 m、新疆天文台南山站25 m等天线纳入天线组阵中。
天线组阵中,特别是涉及异地组阵的时延、时延率和相位差的估计与补偿,以及信号合成等方法是天线组阵的关键技术。天线组阵技术在航天工程中的应用在国内尚属首次,密云站和武清站的直线距离约110 km,与昆明站的距离超过2100 km,属于异地组阵。异地组阵与本地组阵相比,由于接收探测器下行信号的路径不同,不同地点的天线接收系统接收到的信号会产生较大的时延和时延率;由于对流层的不稳定性,使得对流层延迟可以在很短的时间、很小的区域内发生变化[12],对流层延迟的预测准确率一般不足70%,湿延迟的预测准确率更是不到30%。这些因素对信号合成效率都有较大影响。
为此,开展了信号时延、时延率和相位差的估计及信号合成方法的研究,提出了利用模型计算和基于科斯塔斯环的搜索估计相结合的初始时延和多普勒频差快速估计方法,并利用现有的密云站GRAS-1天线和昆明站GRAS-2天线,以嫦娥3号着陆器数传信号作为实验对象,进行了天线组阵与数据接收技术检验实验。
1 火星探测数据接收天线组阵合成性能分析
1.1 数据接收天线组阵方案
图1为首次火星探测天线阵组成及信号合成数据处理流程示意图。探测器信号由地面站天线接收经下变频后,由检前信号采集设备进行中频信号采集、处理,通过网络发送到组阵信号合成和解调处理机进行信号合成和软件解调。下变频器和检前采集设备由站内原子钟提供的频标信号作为外频标。组阵信号合成和解调软件实现各路信号之间的时延、多普勒频差和相位差等参数估计,完成信号幅度、时延、条纹旋转和相位的补偿和修正,并将修正后的数据进行加权相加实现信号合成。合成信号由软件解调模块实现软件解调。
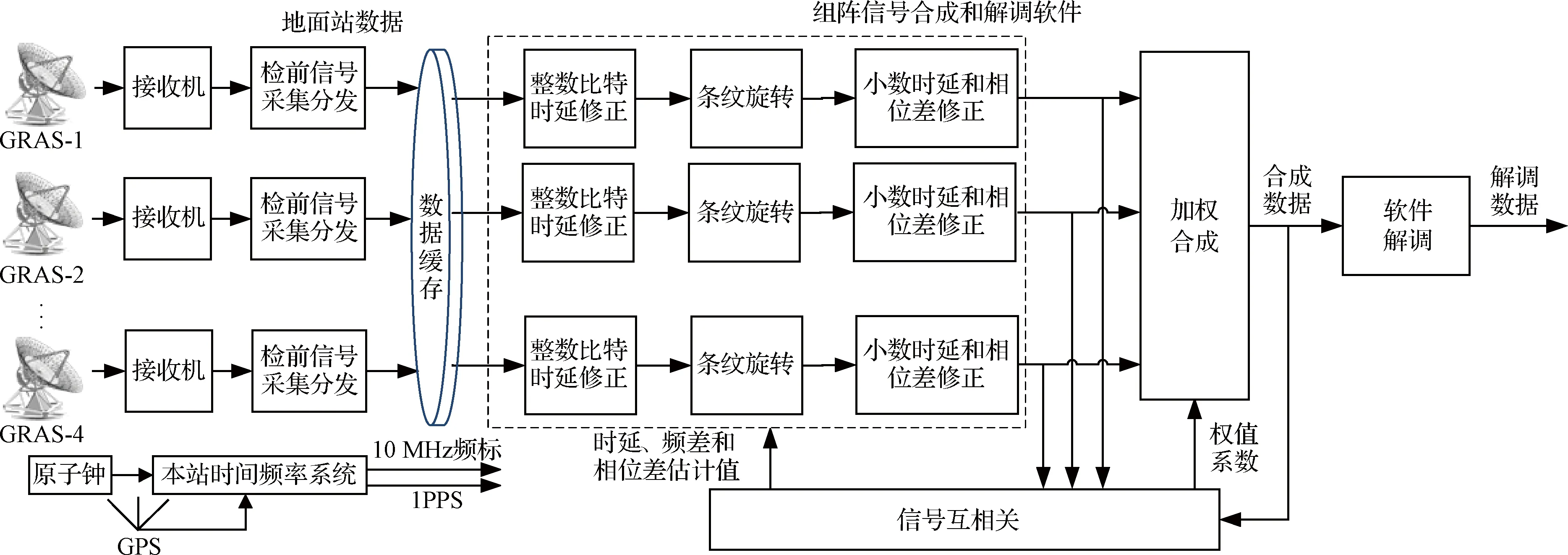
图1 天线阵组成及信号合成数据处理流程示意图Fig.1 Antenna array and the combining flow diagram
用于天线阵信号合成处理的基本方法主要有全频谱合成(FSC)、复符号合成(CSC)、符号流合成(SSC)、基带合成(BC)和载波组阵(CA)等。其中,复符号合成和基带合成适用于存在副载波的情况,载波组阵主要适用于本地组阵,符号流合成效率较低,全频谱合成方法具有更高的合成效率和更广泛的信号适用能力[2]。为此主要针对合成效率和信号适应能力最强的全频谱合成方法进行研究。
1.2 天线阵信号合成性能分析
假设每个天线对的残留相位误差呈高斯分布,以天线1为参考天线,则FSC合成损失可表示为[13]
(1)
式中:RFSC为FSC合成信号的实际信噪比,Rideal为无合成损失时的合成信号理论信噪比,Ri为天线i的信噪比,Cij为由于天线之间相位未对齐引起的减弱系数,且
Cij=E{exp[j(Δφi1-Δφj1)]}=
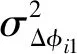
式中:Ri1为天线i的信号与参考天线1的互相关函数的信噪比,即
Ri1=2RiR1TB
式中:T为积分时间,B为信号带宽。
理论上信号信噪比越低,合成损耗越高,选择合成后的信号信噪比为解调门限时进行指标分析。由LDPC译码的Eb/N0≤0.5 dBHz(编码后)的门限要求,以及GRAS-1、2、3和4天线G/T值,计算合成信号达到解调门限时每面天线信号的信噪比。此时单路天线信噪比均低于解调门限,合成信号Eb/N0达到0.5 dBHz解调门限要求。经计算,不考虑大气相位扰动,在采用全频谱合成SIMUPLE互相关算法时,在码速率≥256 bps,频标频率稳定度≥2×10-11时,GRAS-1/2/3/4天线阵可以实现合成损失≤0.35 dB。一般条件下,铷种、氢钟等的短期稳定度均可满足这一条件,但考虑大气扰动和接收设备等因素对相位稳定性的影响,一般选用短稳精度较高的氢钟作为频率标准。在首次火星探测任务中,下行数据最低码速率为16 kbps,所以GRAS-1/2/3/4天线阵可以满足火星任务及后续其他深空探测任务的信号合成性能要求。
2 信号合成方法和处理流程
信号合成首先根据探测器轨道进行时延、频差的模型计算或基于信号的初步估计,进行信号时延和频差的粗修正;通过互相关实现时延、频差和相位差的精确估计和修正,然后进行信号的加权合成;合成后的信号通过软件解调实现下行数据的获取。
2.1 初始时延、频差和相位差快速估计方法
基于时延模型的初始时延和时延率计算,需要较高的探测器轨道和两站授时精度。在缺少精确先验知识的条件下,直接利用互相关方法进行时延、多普勒频差的估计,需要进行二维搜索,需要较大的计算量和较长的估计时间。为此提出一种基于科斯塔斯环载波跟踪的时延、多普勒频差和相位差的快速估计方法。在实际信号合成处理中,可以与由探测器轨道和天线位置的模型计算相结合,从而极大提高信号的互相关捕获效率和初始估计精度。
时延、多普勒频差和相位差快速估计示意图如图2所示。天线信号经采样后,利用科斯塔斯环实现载波相位的复现和跟踪;输出的同相信号经时延互相关实现两天线信号的时延估计,同时实现载波相位差π弧度的相位模糊估计。复现的载波相位经时延调整后实现两路载波相位的时间同步,然后经载波相位差分后获得载波相位的差值,通过频差和初始相位差估计模块实现频率差和相位差的估计,其中相位差还需要进行π或0弧度的相位补偿。频率差和初始相位差估计模块可采用经典的最小二乘估计方法实现频率差和相位差的估计。

图2 天线信号相位差、时延和频率差快速估计示意图Fig.2 The estimation flow diagram of signal phase difference, delay and frequency difference
与传统的估计方法相比,由于载波跟踪和时延互相关估计都只需要一维搜索,估计速度比传统的二维搜索的互相关方法快得多,同时不需要探测器位置、时延或时延率的先验知识。
2.1.1多普勒频率捕获
深空探测具有较大多普勒频率,对信号进行载波跟踪前需要先进行载波捕获。BPSK信号通常的载波恢复方式是通过平方处理去除信息调制,这种方式可以达到很高的频率分辨率。通过平方处理,完成载波恢复,然后进行傅里叶变换,通过计算幅度谱最大值对应的频率实现载波频率的估计。图3(a)给出了嫦娥3号下行信号的功率谱,图3(b)为平方谱,可以看出与功率谱相比平方谱具有很高的频率分辨率。
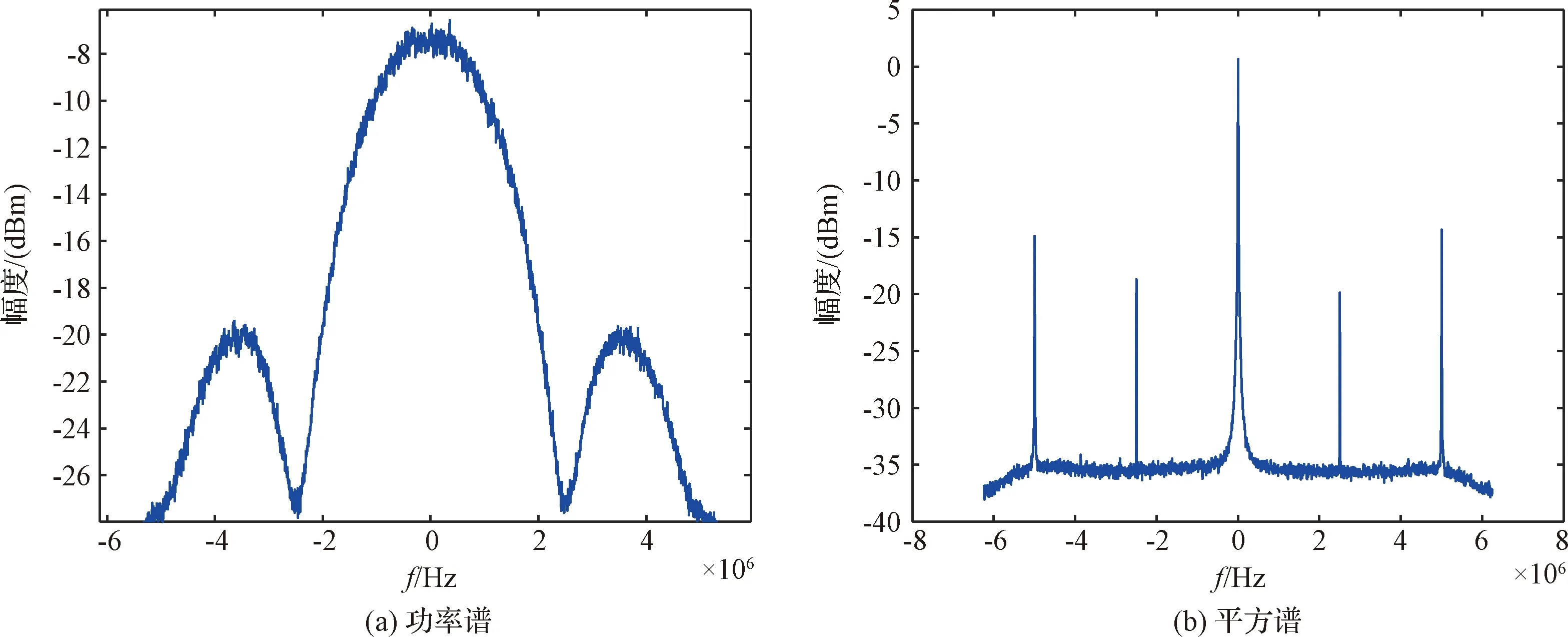
图3 嫦娥3号下行信号功率谱与平方谱Fig.3 The power spectrum and square spectrum of CE-3 downlink signal
由于平方运算的非线性,噪声自相乘以及噪声信号交叉项导致信噪比恶化,尤其是低信噪比条件下,将导致噪声方差急剧增大。在输入信噪比小于0 dB以后,随着信噪比降低,平方后的信噪比急剧恶化。在低信噪比情况,可以采用基于循环相关的载波频率估计方法。由于调制信号是周期平稳的,其不同谱分量之间具有相关性,而这一相关性是噪声所没有的,因此这种处理方式可以有效抑制噪声的干扰。
2.1.2基于软件科斯塔斯环的载波跟踪
科斯塔斯环载波跟踪模块结构示意图如图4所示,通过载波跟踪获得两路天线信号的同相信号,并分别获取两路天线信号的载波相位。

图4 基于软件科斯塔斯环的载波跟踪结构示意图Fig.4 The diagram of carrier tracking structure based on software Costas ring
软件科斯塔斯环由两个相正交的环路构成,每个环路包括第一乘法器、低通滤波器、第二乘法器、环路滤波器和数字控制振荡器(NCO),两路环路共用一个环路滤波器和NCO。NCO分别和两路互相正交的环路构成锁相环;NCO分别向两个环路提供互相正交的正弦载波和余弦载波,并分别输出至两个环路中的第一乘法器。
2.2 基于互相关的精确时延、频差和相位差估计
假设两路天线信号之间的时延、频差和相位差在短时间内近似为常数,则它们的最大似然估计可表示为[14]
(2)

x1(t)=A1a(t)exp[j(2πf1t+φ1)],x2(t)=A2a(t-τ0)exp[j(2πf2t+φ2)]
式中:A1和A2是信号幅度;a(t)是调制信号;τ0为信号时延;f1和f2分别为信号中心频率,由于多普勒频率影响,两者存在频差;φ1和φ2为信号初始相位。则式(2)可近似为
exp[-j(2πΔft+Δφ)]}dt
(3)
式中:Δf为信号多普勒频差估计值。上式的频域形式可表示为
exp[-j(2πτf+Δφ)]}df
(4)
在时延、多普勒频差和相位差经过粗修正后,由式(4)可以看出,互相关函数的相位谱与时延值和相位差存在线性关系,可以通过在频域下利用互相关函数的相位谱进行时延和相位差的最小二乘估计;由式(3)可以看出,多普勒频差和相位差与时域互相关相位存在线性关系,可以利用时域互相关函数进行频差和相位差的最小二乘估计。
如果来自各天线信号的信噪比(SNR)足够高,所有天线对都可进行很强的相关,则无需特殊处理,直接利用从相关获得的相位和延迟偏移来对齐信号即可。然而,当来自各天线信号的SNR较低时,通常必须采用其他方法来进行相位估计。用信号相关来确定对天线信号的幅度和相位进行修正的复加权值,主要存在SIMPLE、SUMPLE[15-16]、EIGEN[17-18]和LSFIT[19]等几种算法。在这些算法中,EIGEN和LSFIT计算量较大,SIMPLE和SUMPLE计算量较小;从合成效率和计算量来说SUMPLE算法具有最好的合成性能。在首次火星探测任务中将主要采用SIMPLE和SUMPLE互相关方法进行信号合成。
2.3 时延、频差和相位差补偿
2.3.1时延补偿
时延可以分为整数部分和小数部分,整数部分的对齐可以通过移动数字信号来实现。根据时延值和采样速率计算时延整数位数,通过改变数据对应的指针位置实现时延的整数位补偿。
时延值的小数部分小于一个采样周期,无法直接通过数字信号平移实现,一般采用时域滤波或插值、频域相位调整的方法实现。根据傅里叶变换的平移性质,将时延值小数部分的补偿通过频域的相位补偿实现,如下式所示[20]
X′(f)=X(f)exp(-j2πfτf)
(5)
式中:τf为小数部分时延。
2.3.2多普勒频差和相位差补偿
由于多普勒频移的不同,在进行相关时需要事先进行条纹旋转。由于传输介质和接收设备的影响,信号具有不同的初始相位。条纹旋转和相位补偿一般采用具有较好精度的时域补偿,并对信号波形影响最小。条纹旋转和相位差的时域补偿可表示为[21]
x′(t)=x(t)exp[-j(2πΔft+Δφ)]
(6)
式中:Δf和Δφ分别为信号间的多普勒频差和相位差。
3 天线组阵数据接收技术实验验证
针对嫦娥3号着陆器X频段2.5 Mbps的下行数传信号,利用密云站GRAS-1和昆明站GRAS-2天线进行了组阵实验,图5为GRAS-1和GRAS-2天线照片。天线信号经数传通道高频制冷接收机、光端机及光纤传输、下变频器和检前记录仪等设备实现嫦娥3号数据的采样和记录。其中,下变频器从站内时频系统输入10 MHz频标信号作为外频标,检前记录仪输入10 MHz频标和1PPS信号作为外频标和时间同步信号;时频系统采用氢原子钟作为输入频标。

图5 GRAS-1和GRAS-2天线Fig.5 The picture of GRAS-1 and GRAS-2 radio telescope
为检验低信噪比情况下的信号合成性能,通过将两天线指向逐步偏开信号源,进行了低信噪比接收的组阵实验。2015年4月7日至2016年4月23日,共进行了52天的组阵观测实验,单站观测数据量超过8TB。
3.1 符号流合成验证结果
利用2015年5月2日的观测数据,进行了符号流合成实验。合成流程为通过软件科斯塔斯环实现单路天线信号的载波锁定,然后通过同相信号的互相关计算实现时延和相位差估计,在解调判别前进行信号的时延和相位修正,最后进行信号合成和数据解调。数据采集的参数设置为,信号带宽10 MHz,采样频率12.5 Msps,I、Q正交采样,量化位数为16 bit。
GRAS-1和GRAS-2的信噪比分别为15.83 dB和14.31dB,合成后的信噪比为17.61 dB,合成损失0.53 dB,合成效率为88.5%。合成前后的星座图如图6所示,可以看出合成后的星座图更加趋于集中,分布的发散程度明显收敛。
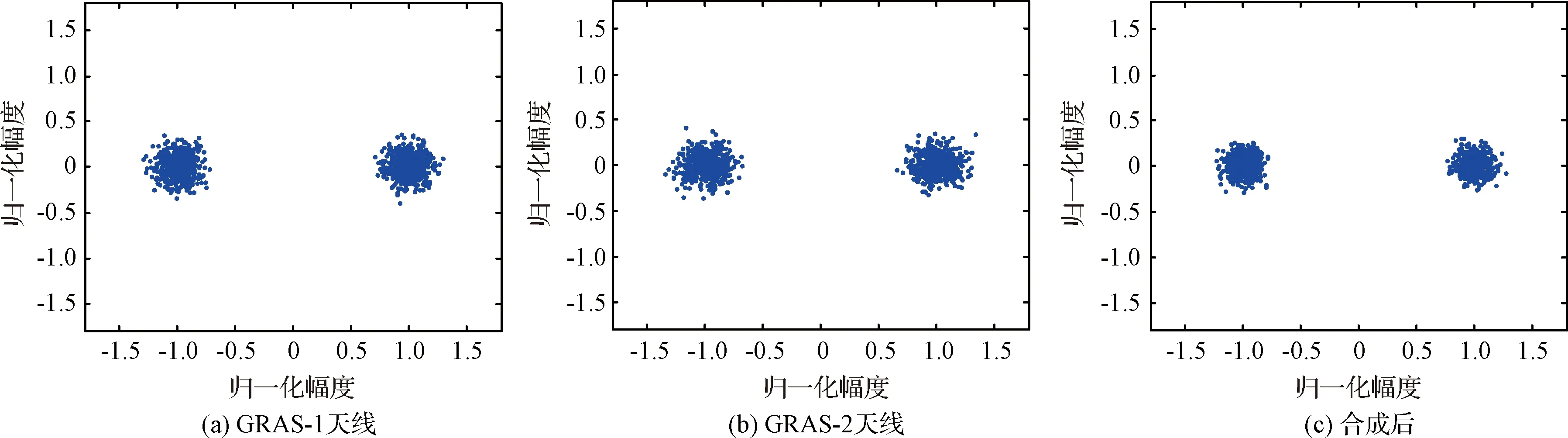
图6 合成前后星座图示意图Fig.6 Constellation before and after combining
3.2 全频谱合成验证结果
3.2.1时延、时延率和相位差估计与补偿实验
对2015年5月2日的组阵观测数据进行了初始时延、时延率和相位差的估计。图7(a)为存在时延残差的互相关系数示意图,图8(a)为存在多普勒频差的互相关干涉条纹。从互相关结果可以看出,在进行时延和频差精确修正前,相关系数和相关频谱的相位与理想的自相关谱存在一定的偏差。通过时延和时延率估计得到时延为5.0×10-7s,时延率为4.11×10-11s/s。将残余时延和频差进行修正,得互相关系数如图7(b)所示,互相关条纹如图8(b)所示。分数时延修正前后的互相关相位谱如图9(a)和9(b)所示。从互相关结果可以看出,互相关系数、条纹和相位谱与理想的自相关谱相吻合。
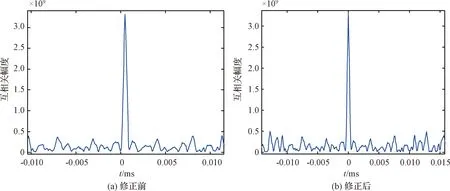
图7 分数时延修正前后的互相关系数Fig.7 Coefficient of cross-correlation before and after fractional delay correction
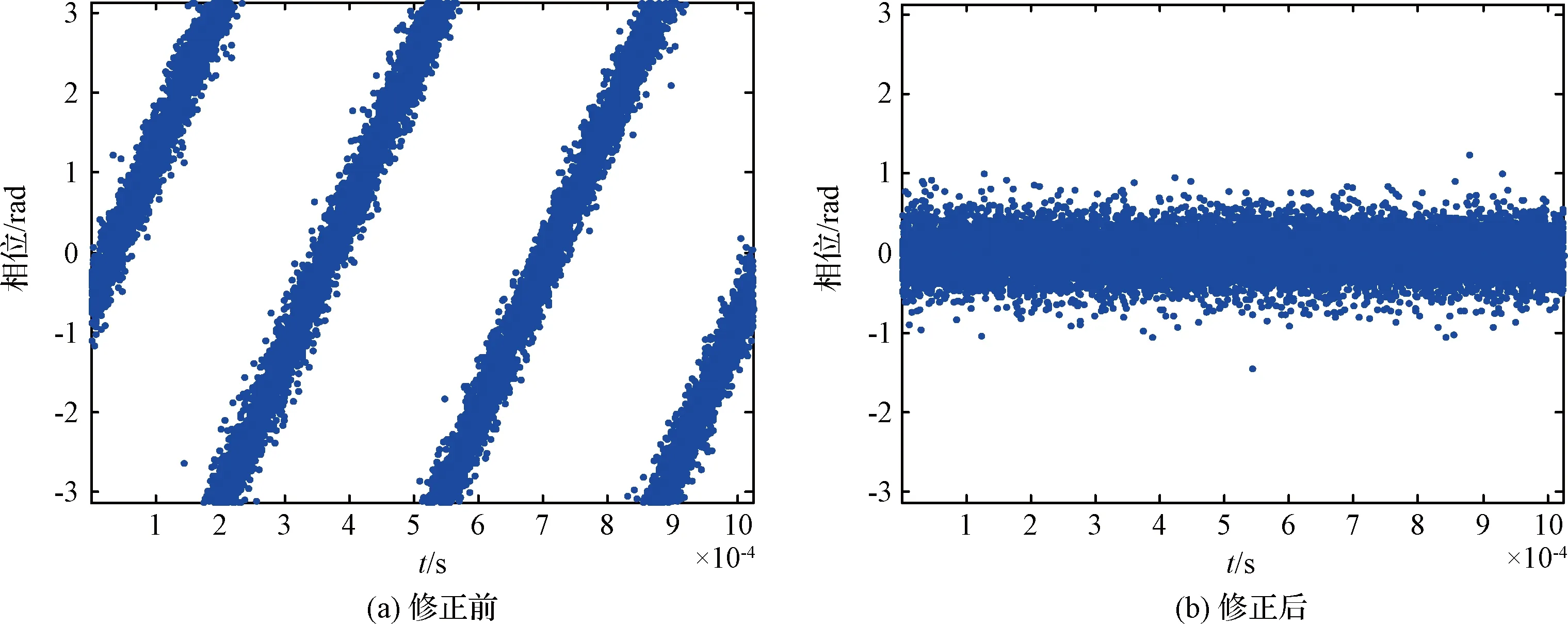
图8 条纹旋转前后的干涉条纹Fig.8 Interference fringes before and after phase rotation
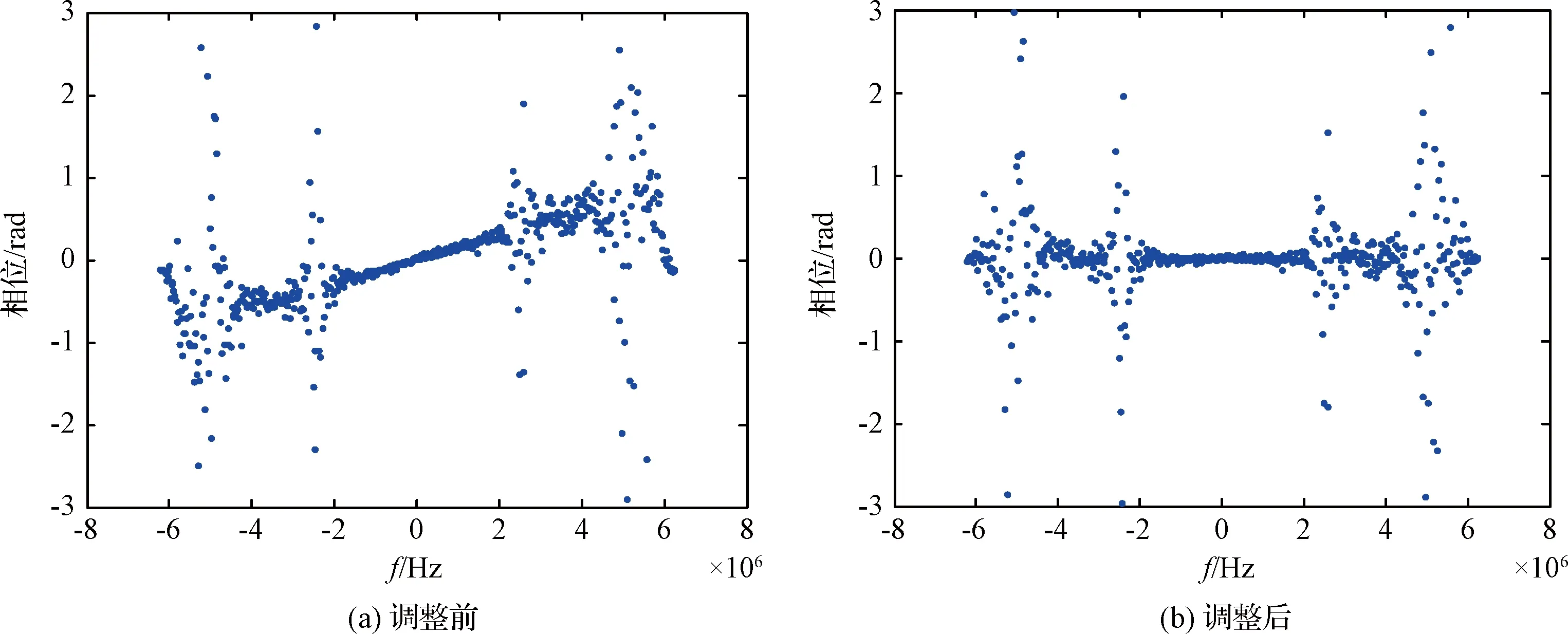
图9 分数时延调整前、后的互相关相位谱Fig.9 Cross-correlation phase spectrum before and after fractional delay correction
3.2.2全频谱信号合成实验
分别利用2015年5月2日、3日、5日、8日以及9月29日、2016年3月29日、2016年4月19日和2016年4月21日的观测数据,进行了低信噪比的全频谱合成实验。2015年9月29日的观测数据是逐步以等间隔角度(50 s)偏开天线俯仰,直至解调机失锁不能正常解调。2016年3月29日的观测数据是通过逐步偏开天线方位角度,使两天线的接收信号信噪比以3dB为间隔下降,直至解调机失锁不能正常解调。2016年4月19日和2016年4月21日的数据是单天线信噪比在0 dB附近以1 dB为间隔下降进行的观测。数据采集时的参数设置为:信号带宽10 MHz,采样频率12.5 Msps,I、Q采样,量化位数16 bit,频标采用外频标。
信号合成验证结果如表1所示,合成前后信噪比如图10所示,合成效率随信噪比变化曲线如图11所示。从实验结果可以看出,50 m天线信噪比从-15.23~17.43 dB,40 m天线从-14.09~15.40 dB,合成信号信噪比覆盖了-11.91 dB~18.86 dB的范围,合成损失最大为0.45 dB,合成效率不低于90.2%。图12(a)为合成前后的功率谱(2015年5月2日数据)示意图,图12(b)为合成前后信噪比随时间变化曲线;图13为合成前后解调判决前的信号波形示意图;从中可以看出合成前后的波形一致,且合成后的信号具有更高的信噪比。
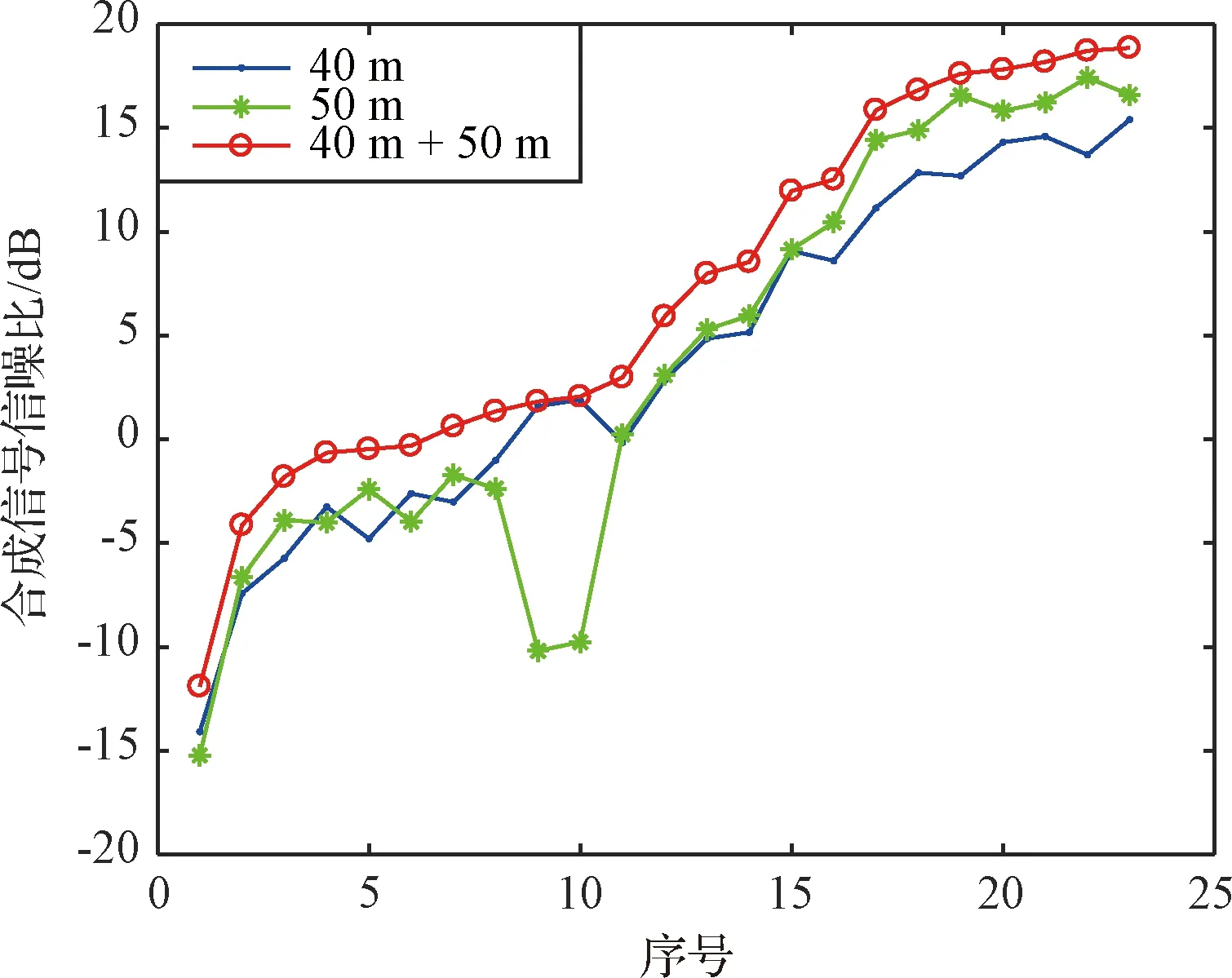
图10 合成前后信噪比示意图Fig.10 SNR before and after combining
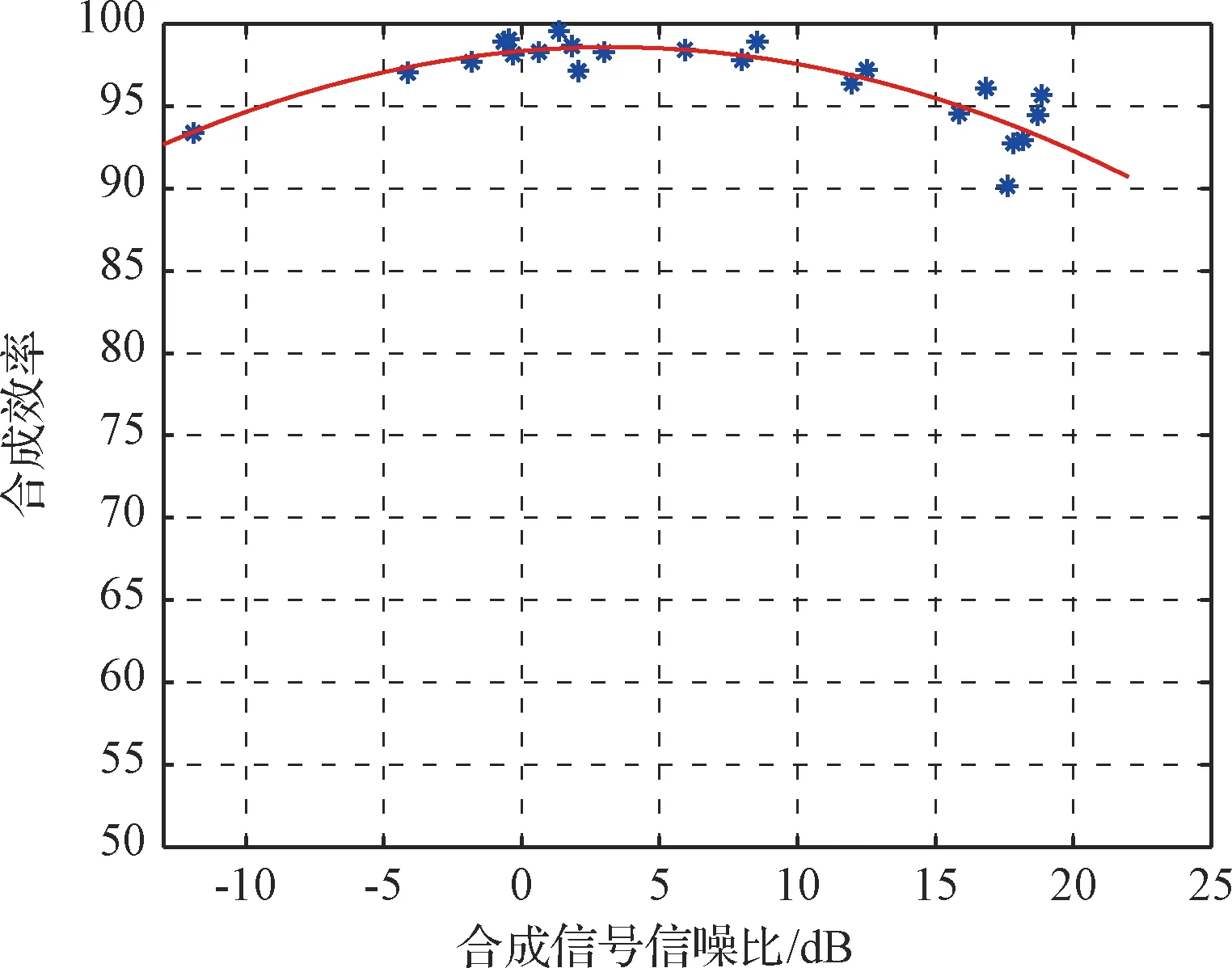
图11 合成效率随信噪比变化曲线Fig.11 Combining efficiency with SNR curve
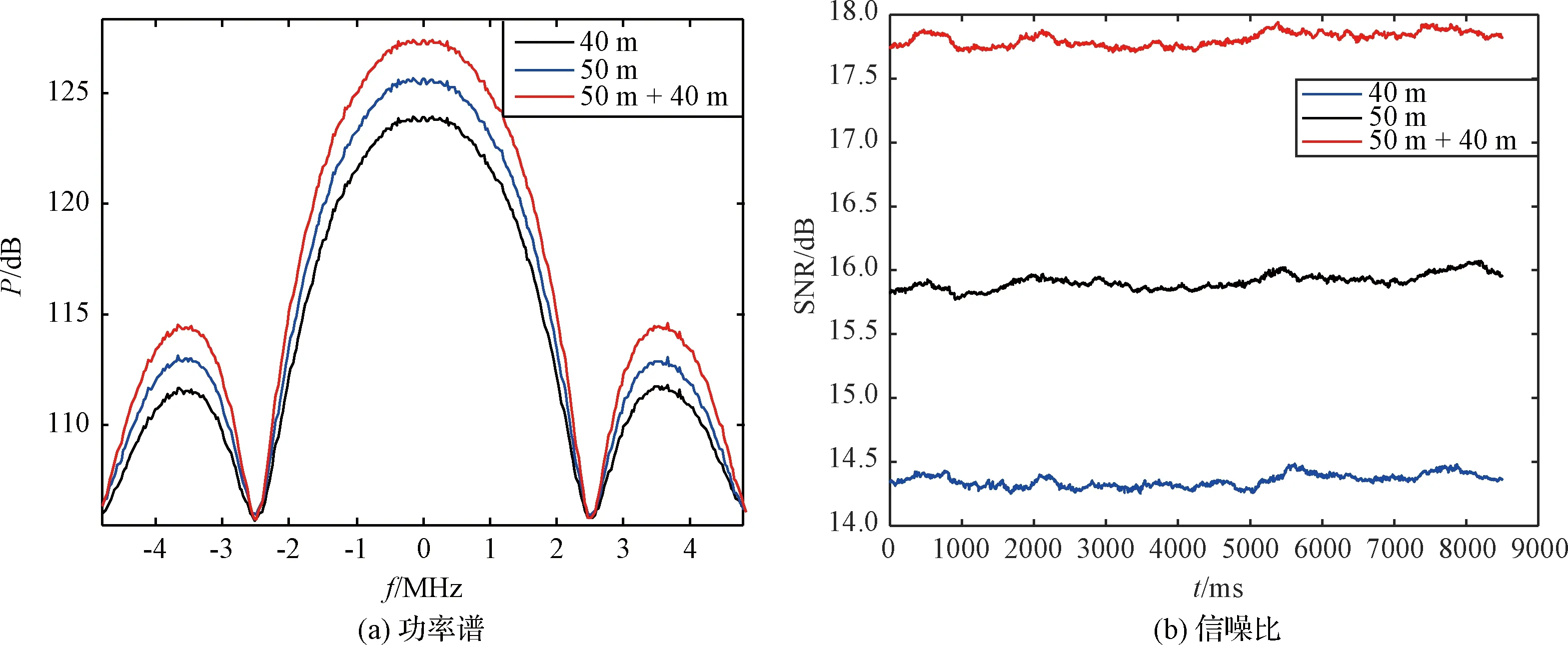
图12 合成前后的功率谱和信噪比随时间变化曲线Fig.12 Power spectrum and SNR curve before and after combining
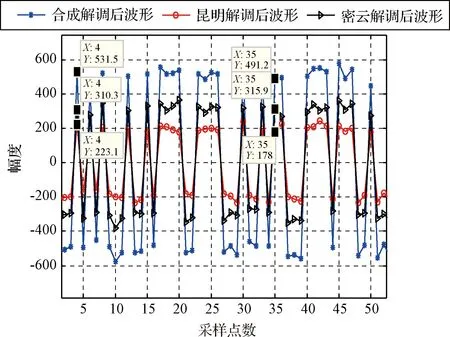
图13 解调判决前的信号波形Fig.13 Signal waveform before demodulation decision
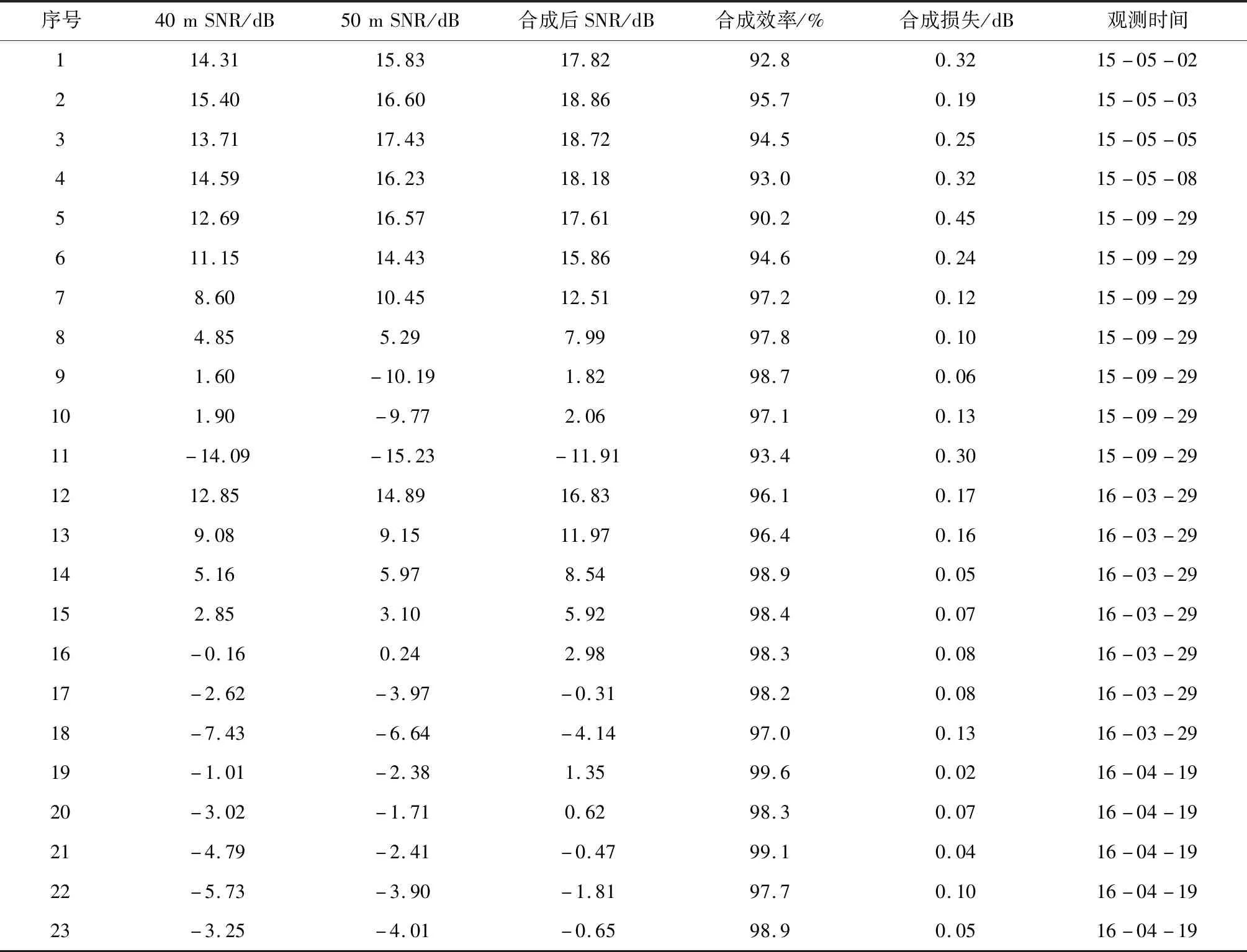
表1 合成验证结果(外频标)Table 1 The combining experiment results (External frequency standard)
2015年5月2日的数据选取的是与符号流合成检验实验相同时间的数据,符号流与全频谱合成效果如表2所示。从中可以看出全频谱的合成增益比符号流高0.21 dB,验证了全频谱合成具有更高的合成性能。

表2 符号流和全频谱合成效率对比Table 2 The combining efficiency comparison of SSC and FSC
为了验证频标误差对信号合成性能的影响,2016年4月21日的数据采用了内频标。图14给出了2016年4月19日和21日的数据合成损失对比情况。从中可以看出采用氢钟作为外频标的观测数据合成性能明显优于内频标数据,合成损失平均比内频标降低0.07 dB。
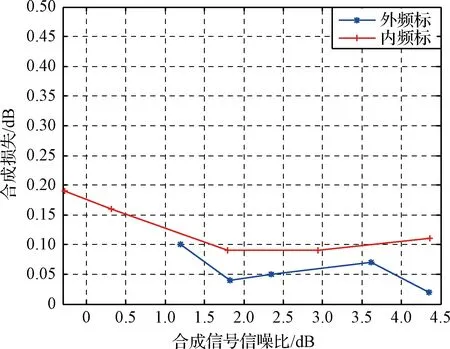
图14 内外频标合成损失对比Fig.14 Comparison of combining loss using internal and external frequency standard
3.2.3月面噪声对信号合成性能的影响

图15 月面噪声对信号合成损失的影响示意图Fig.15 Influence of Moon surface noise on combining loss
从图11中的合成效率变化曲线可以看出,在高信噪比时合成效率随着信噪比的降低而增大,在低信噪比时合成效率随信噪比降低而减小,这一现象不完全符合全频谱合成性能随信噪比降低而下降的规律。说明两站接收的噪声存在一定的相关性,并且随着天线逐步指向探测器,相关噪声也逐步增大。产生的主要原因是由于两天线接收的月面噪声存在相关性,Dewey对背景展源对信号合成的影响进行了详细分析[22]。当天线指向逐步偏离月面时,月面亮温度造成的影响也逐步减小。嫦娥1号微波辐射计的观测结果,月球白天7.8 GHz的表面亮温度为60 K~245 K,且赤道亮温最高,向两极逐渐降低[23]。另外,由于月面噪声的存在,一定程度也会影响探测器信号相位差的估计精度,在低信噪比时将会更加明显[24]。
图16给出了2015年9月29日的实验数据合成后噪声实际功率与理论噪声功率的差值、合成后信号实际功率与理论功率的差值和信号合成损耗等与合成后信噪比之间的关系,可以明显看出上述规律;在合成后信噪比为20.6 dB的高信噪比时,合成后噪声实际功率与理论噪声功率的差值达到0.44 dB,合成损失达到0.45 dB,高于低信噪比时的合成损失。
4 结 论
通过对天线组阵的关键技术,特别是涉及异地组阵的时延、时延率和相位差的估计与补偿,以及信号合成等关键技术的研究,提出了利用模型计算和搜索估计相结合的初时延和时延率快速估计方法。利用现有的密云站GRAS-1天线和昆明站GRAS-2天线,以嫦娥3号着陆器数传信号作为实验对象,开展了天线组阵与数据接收信号合成实验验证。
研究和实验结果表明,全频谱合成方法优于符号流合成方法,其合成损耗小于等于0.45dB,可用于我国火星探测任务天线组阵的信号合成;初始时延和时延率快速估计方法可提高广域组阵信号互相关的搜索效率;所确定的信号合成技术流程和数据处理方法可用于我国首次火星探测信号合成接收软硬件设备的研制和开发。
后续的研究中,将对月球、火星等展源干扰信号对信号合成性能的影响进行进一步分析研究,并对合成流程进行优化,以期进一步提高信号合成性能。

