基于多层卷积网络的圆弧快速检测算法设计

张智凡，于凤芹

(江南大学 物联网工程学院，江苏 无锡 214000)

0 引 言

图像处理技术在地理信息、建筑、电子、机械等领域中得到了广泛应用，特别是对工程图纸的理解与识别过程，更是极大地依赖于图像处理技术[1]。而在工程图纸理解与识别中，最主要的基础图元就是圆弧，因此对圆弧进行准确迅速的检测是工程图纸理解与识别领域的一个关键问题，也是工件尺寸测量领域的一个重要问题[2]。

圆弧检测的基础算法是霍夫变换算法。随机霍夫变换可以克服计算量大[3]、占用内存大、无法在线实时检测的缺点，但是由于随机抽样会产生很多无效点集，会增加搜索时间并且降低在复杂背景图像中的检测效率和精度[4]。概率霍夫变换可以解决前两种算法耗时的问题，在选择拟合点时采用了随机抽取的方式，并加入了计数器，当直线被拟合出的次数达到一定阈值时取出这条线并完成拟合，增加了检测实时性[5]。有学者在霍夫变换算法的基础上提出了一系列优化的圆弧检测算法，文献[6]通过找出可能位于圆外边界上与圆相切的线段，根据切线段估计圆心半径，得到候选圆集合并进行数据合并，对每一个候选圆进行跟踪检测来判断其为圆或弧。但该方法在匹配切线的过程中确定候选圆，易导致误检情况的发生。文献[7]提出了一种利用统一多尺度深卷积神经网络进行快速目标检测的方法，但是该方法的检测精度存在一定的影响范围，难以保证整体的高准确性。文献[8]利用确定的椭圆中心为匹配参考点逐行匹配圆弧特征点，然后利用改进的RANSAC算法排除误匹配对，但是计算量大，匹配成功率偏低。

针对现有方法中存在的误检率较高、检测效率低的问题，文中提出一种基于多层卷积网络的圆弧快速检测算法，以提高圆弧检测算法的计算效率与准确度。首先基于多层卷积网络进行圆弧信息的聚类存储，并将缺损比例在三分之一以下的圆弧排除，再对其他圆弧进行全局聚类。该过程减小了噪声和缺损圆弧的干扰，提高了圆弧检测效率。然后以圆弧的圆心所在区域为依据对圆心阈值区域进行重构，获取圆弧阈值区间。最后对阈值区间进行优化，并对圆弧进行拟合和去伪，实现圆弧的快速检测。

1 基于多层卷积网络的圆弧快速检测算法设计

1.1 圆弧检测原理

大量物体具有圆弧轮廓，可以通过检测圆弧来识别物体的存在，并可利用其实现产品质量评估、提高生产效率等。圆弧检测的基本原理是在对圆弧图像识别的基础上，对圆弧特征信息进行提取、储存、分析和判断，并优化霍夫变换算法，实现对圆弧的检测。

一般情况下，对圆弧图像的识别需借助机器视觉技术，其识别过程如图1所示。

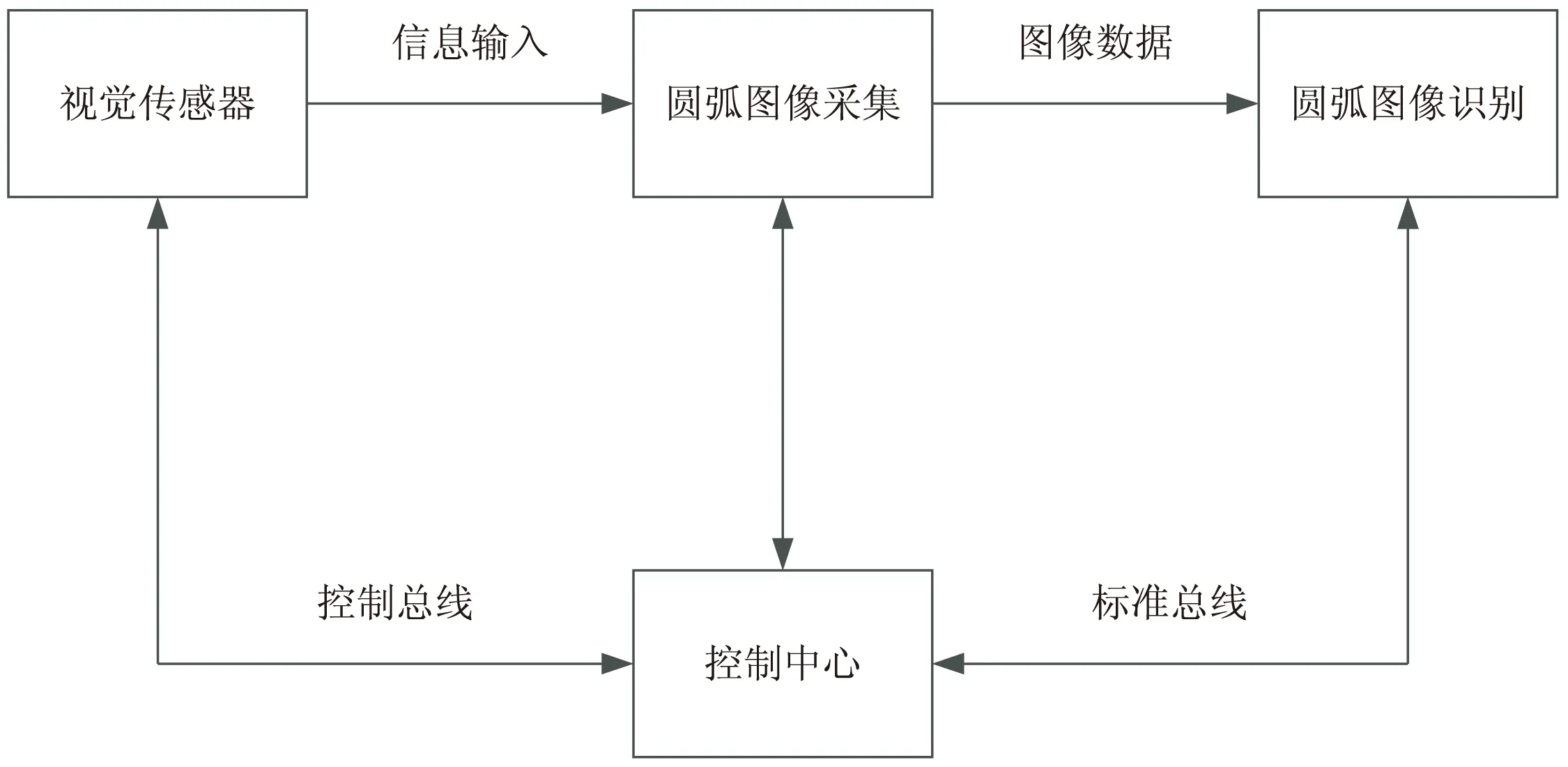
图1 基于机器视觉技术的圆弧图像识别过程

在此基础上，从机器视觉的识别结果中提取圆弧的特征信息，并将其中夹杂的噪声滤除，对目标图像的信息加强，再对其进行提取、储存、分析和判断，继而对基础的霍夫变换算法进行优化，完成对圆弧信息的检测。其中，霍夫变换算法是利用图像空间和霍夫参数空间的线-点对偶性，把图像检测过程由图像空间转换到参数空间中进行。

1.2 基于多层卷积网络的特征点提取及圆弧信息的聚类存储

首先利用多层卷积网络实现圆弧信息的聚类存储[9]。多层卷积网络是一种可用于进行图像特征识别的感知器模型，其中包括卷积层、Maxout层、池化层和全连接层。其中，卷积层用于提取特征，Maxout层利用Maxout激活函数实现信息筛选，池化层用于选择特征，全连接层用于分类。在多层卷积网络中，在两个及以上的卷积层后才会存在一个池化层，即卷积层串联。这是一种优化操作，即通过增加卷积层数来缩小卷积核的尺寸，从而减少网络参数，增加多层卷积层中的非线性操作，使多层卷积网络对特征信息的学习能力更强。

利用多层卷积网络对圆弧信息进行训练，从中提取圆弧的特征信息，并以此为依据对圆弧信息进行聚类存储[10]，具体步骤如下：

①利用卷积核扫描所输入的图像，逐个扫描图像中的所有像素点。在扫描过程中将最先找到的特征像素点记录为p，并自上而下对其进行初始化检测，规定其初始化值为0[11]。

②分别检测p上方位的右、中、左三个位置，当检测到对应位置的特征像素点后将其记录为q1，并在数组中储存q1的坐标位置，将其像素值初始化为0。对p左、右两方位的像素点进行检测，检测到像素点后对其进行标记并储存坐标点位置，检测不到像素点时则退出聚类[12]。

③分别检测p下方位的右、中、左三个位置，当检测到对应位置的像素点后将其记录为q2，并在数组中储存q2的坐标位置，将其像素值初始化为0。按照步骤②中的方法对q2的左、右两方位的像素点进行检测。

④分别对p左、右两个方位的像素点进行检测，将检测到的像素点分别记录为q3、q4，并在数组中存储q3、q4的坐标位置，将其像素值初始化为0。按照步骤②中的方法对q3、q4的8个方位的像素点进行检测。

⑤以方位标记为依据，当方位标记是上方位时，进行步骤②的操作，当方位标记是下方位时进行步骤③的操作，当方位标记是左右方位时进行步骤④的操作[13]。

不断重复上述步骤即可在卷积层中得到圆弧图像的特征信息，经过Maxout激活函数筛选得到特征图，然后在池化层池化这些特征。池化操作是为了进一步减少网络参数，防止多层卷积神经网络过拟合。然后在全连接层输出标记特征结果，如下所示：

(1)

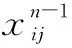
根据上述特征输出结果进行聚类及存储，其过程如下：

·随机选取k个特征像素点作为初始中心点，即共有k个类；

·计算其余特征像素点到这k个中心点的距离，从中选择距离最小的中心点；

·重新计算k类的质心作为新的中心点；

·迭代步骤2和3，直到达到最大的迭代次数，输出聚类中心集并在数组中存储。这样，通过聚类方向自带的惯性作用即可加速圆弧的检测，并且能够将数目较少的孤立像素点当做噪声信息直接过滤[14]。

1.3 圆弧全局聚类

完成圆弧信息的聚类存储后，对圆弧进行全局聚类，即把不相接的、一个椭圆中的圆弧划分至一处。将缺损比例在三分之一以下的圆弧排除，对其他圆弧进行全局聚类，聚类依据为包含像素点的具体数量。如图2所示，圆弧a1为待聚类的对象，首先对a1的搜索区域进行定义，对圆弧a1与搜索区域中的圆弧进行全局聚类。该搜索区域的定义为圆弧a1的弦J3、J4,切线τ1、τ2以及图像边界所构成的区域。接下来对搜索区域内能够与圆弧a1进行全局聚类的其他圆弧进行搜索：过圆弧a1的末端点与首端点作与J3、J4平行的直线，当该直线与切线τ1、τ2相交时可获得两个交点，当其他圆弧的首端点与末端点都位于搜索区域之内，即说明该圆弧位于圆弧a1的搜索区域内[15]。

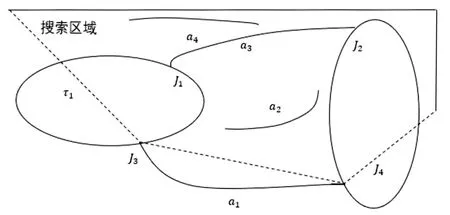
图2 圆弧搜索区域定义

利用弧中心、弦中心距离条件对圆弧是否属于同一椭圆进行确定：

(2)

‖Pm/2,1Pn/2,2‖>‖C2Pm/2,1‖

(3)

如图3所示，C1、C2、C3分别代表弦b1、b2、b3的中点;Pm/2,1、Pn/2,2、Ps/2,3分别代表圆弧a1、a2、a3的中点;m、n、s分别代表圆弧a1、a2、a3的点数，当下标不能整除时可进行四舍五入。通过式(2)、式(3)可排除搜索区域内不属于一个椭圆的圆弧。

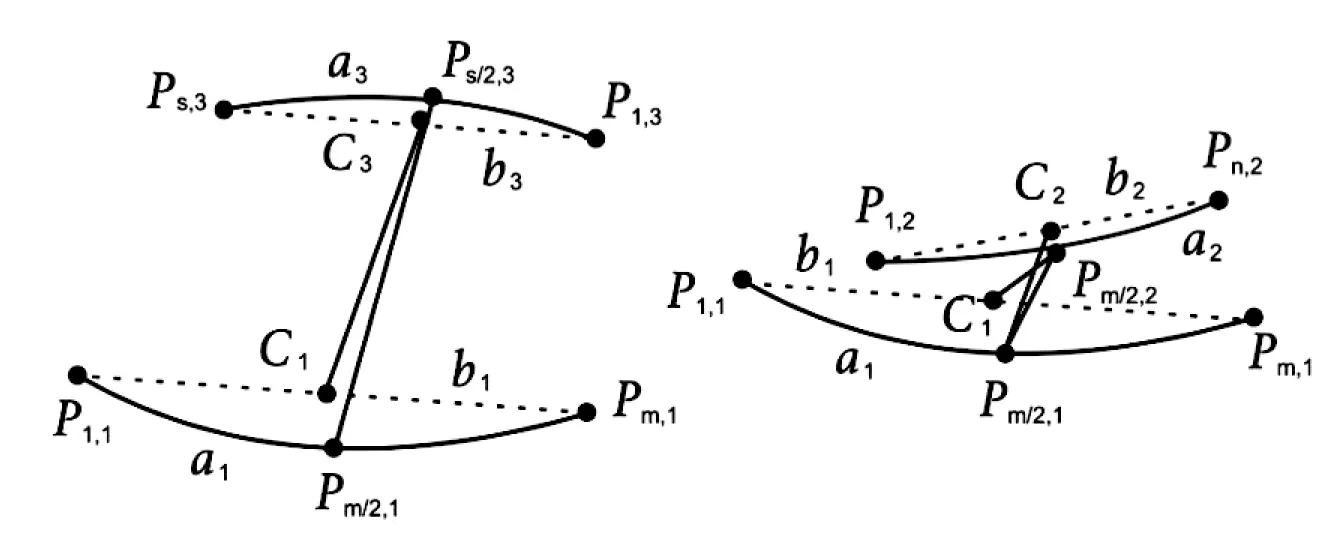
图3 去除圆弧a2

1.4 圆弧阈值区间的获取、优化

完成圆弧全局聚类后，对其进行阈值区间获取[16]。以圆弧的圆心所在区域为依据对圆心阈值区域进行重构：在数组中利用三弦比例对圆弧上最短的采样点间隔长度进行确定，并按照顺序获得n组采样点以对圆心分布区域进行计算，其中分布如图4所示。在计算时，每次都需要在参数空间中对对应的格子累加器进行加一操作。对参数空间中持有最大累加值的格子位置进行统计即可获得圆弧的圆心所在区域。对该区域的纵坐标与横坐标进行分布范围记录，以计算圆心区域的构筑边长，计算公式如下：

(4)

其中，L表示圆心区域的构筑边长；H表示横坐标分布范围的差值；V表示纵坐标分布范围的差值；Hu、Hb表示横坐分布范围的横纵坐标；Vu、Vb表示纵坐标。构筑以圆心为中心，边长为L的正方形区域即为圆弧的阈值区间。

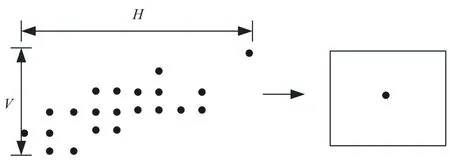
图4 阈值区间示意图

完成圆弧阈值区间获取后，需要对其阈值区间进行优化，并对圆弧进行拟合和去伪，以实现圆弧的快速检测[17]。其中阈值区间的优化策略如表1所示。

表1 阈值区间优化策略

而圆弧的拟合和去伪需要对候选弧对与圆弧的有向边界列进行提取，并利用最小二乘法对候选圆的参数(p,q,r1,r2,θ)进行计算。并对候选圆上是否存在边界像素进行判断：

(5)

当di的值不属于圆弧的阈值区间时，将候选圆排除。直到各个圆弧都找到对应的圆，完成圆弧的拟合和去伪，实现圆弧的快速检测。

1.5 基于多层卷积网络的圆弧快速检测算法步骤

基于多层卷积网络的圆弧快速检测算法的检测过程如图5所示。

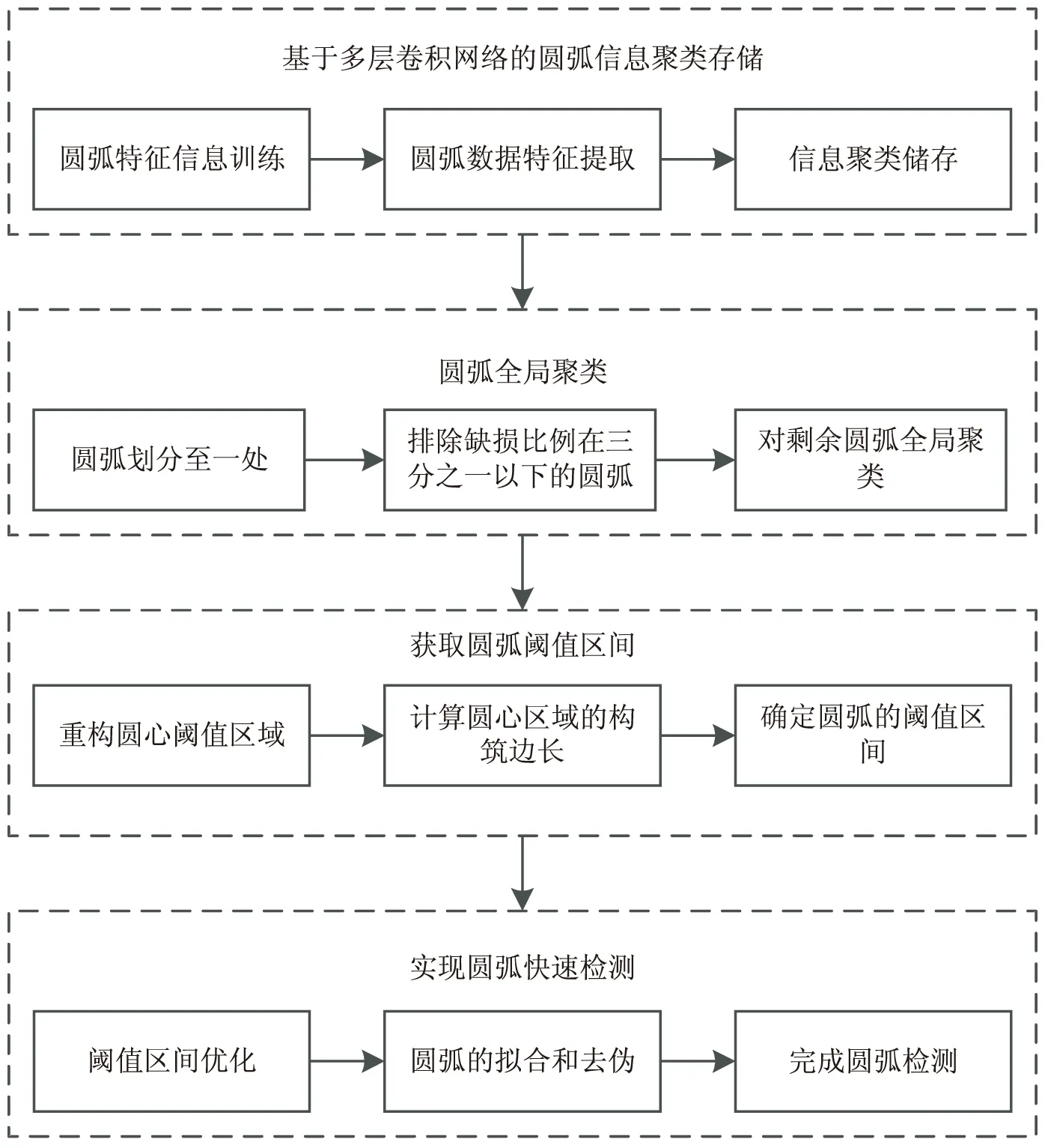
图5 基于多层卷积网络的圆弧快速检测过程示意图

根据图5可知，所设计的基于多层卷积网络的圆弧快速检测算法首先是借助于多层卷积网络实现了圆弧信息的聚类存储，然后利用圆弧聚类方向自带的惯性作用将数目较少的孤立像素点过滤掉，并对其他圆弧进行全局聚类。在此基础上重构圆心阈值区域，获取圆弧阈值区间，并对阈值区间进行优化，对圆弧进行拟合和去伪，完成对圆弧的快速检测。

2 仿真实验结果与分析

为了检测提出的基于多层卷积网络的圆弧快速检测算法的有效性，设计如下实验，将该方法与文献[6]中的基于切线段匹配的快速圆弧检测算法、文献[10]中的基于边界聚类的圆弧检测算法进行对比。

2.1 实验环境

算法运行的环境为MATLAB 8.0的程序开发环境、Windows 7的操作系统、3G DDRII的内存、2G双核处理器、Technology AMD Turion 的CPU。

在GREC2013测试集中对工件的拟合图片进行选取，图片尺寸为512×512，共6张，利用基于多层卷积网络的圆弧快速检测算法、基于切线段匹配的快速圆弧检测算法和基于边界聚类的圆弧检测算法对其中的圆弧进行检测，观察不同算法的误检情况和检测耗时，比较其性能的优劣。

2.2 实验结果与分析

(1)误检率对比。

利用基于多层卷积网络的圆弧快速检测算法、基于切线段匹配的快速圆弧检测算法和基于边界聚类的圆弧检测算法进行圆弧检测的识别结果如图6所示。

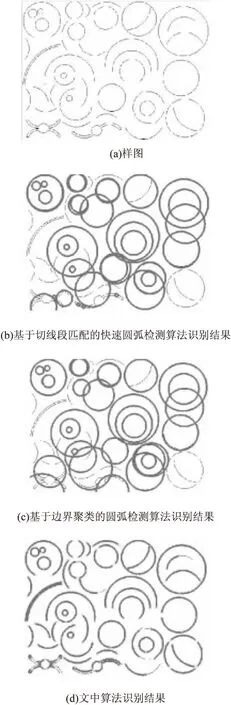
图6 不同算法的检测识别结果

分析图6可知，文中所提算法的检测结果明显要优于另外两种算法，检测结果与样图相符，且噪声较小、清晰度更高。

为进一步验证所提算法的准确性，对比不同圆弧检测算法的误检率，对比结果如表2所示。

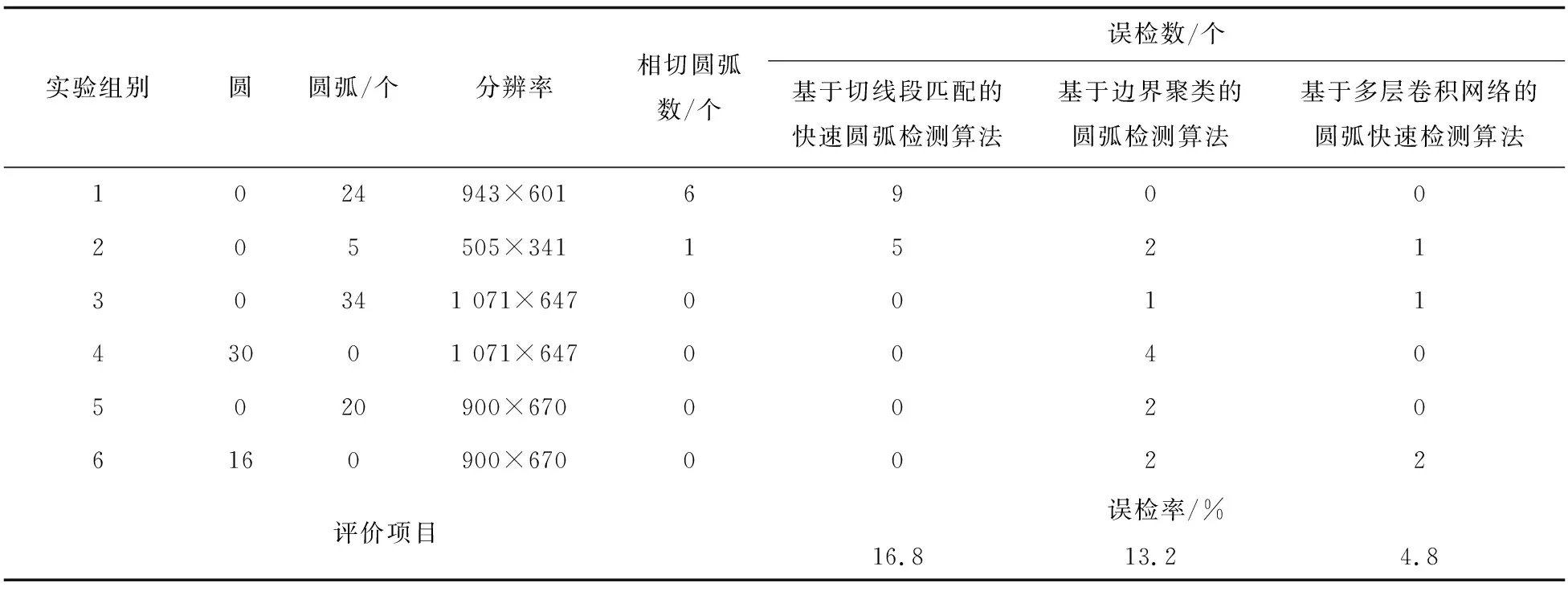
表2 误检率对比结果

根据表2中数据可知，基于切线段匹配的快速圆弧检测算法的误检率为16.8%，基于边界聚类的圆弧检测算法的误检率为13.2%，基于多层卷积网络的圆弧快速检测算法的误检率为4.8%。通过比较可知，所提圆弧检测算法的误检率在三种算法中最低，能够实现对圆弧的准确检测。

(2)检测精度对比。

在一个目标检测过程中，检测结果的质量可从召回率和精度两方面进行评价。召回率和精度成反比例关系，召回率越高则检测精度越低。因此为验证所提圆弧检测算法检测结果的精度，测试不同算法的召回率，得到对比结果如表3所示。

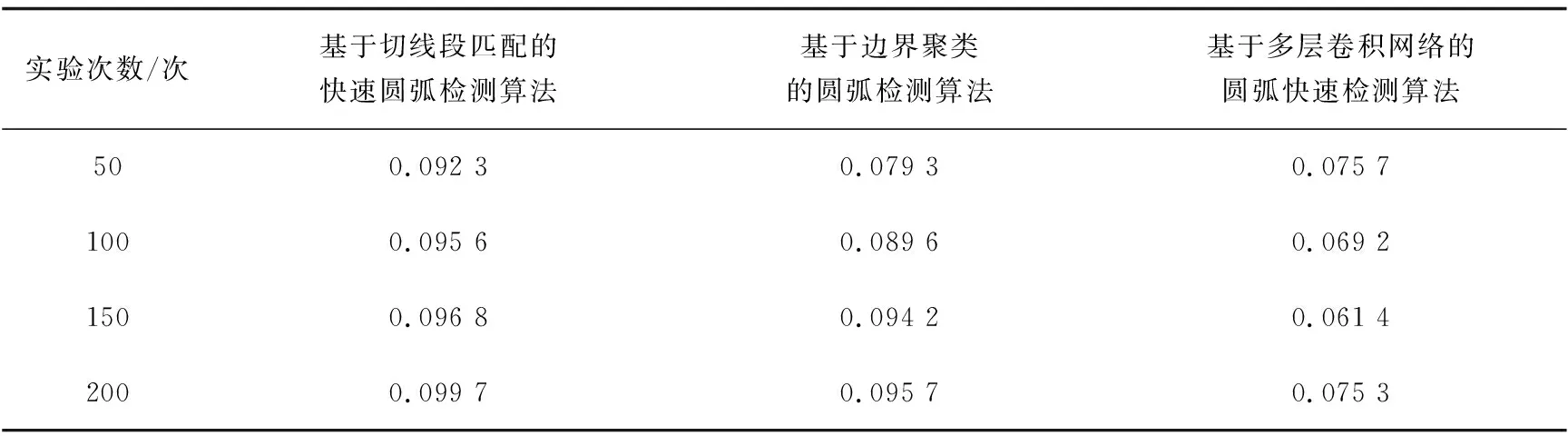
表3 不同圆弧检测算法的召回率对比 %

分析表3可知，随着迭代次数的增加，不同算法检测结果的采集召回率也在不断发生变化。基于边界聚类的圆弧检测算法召回率的变化幅度在三种算法中最大，但是召回率比基于切线段匹配的快速圆弧检测算法略小。所提算法的召回率在三种算法中始终最低，证明该算法的检测精度最高。

(3)检测效率对比。

为检验所提圆弧检测算法的检测效率，测试相同实验次数下不同算法的检测耗时，结果如图7所示。

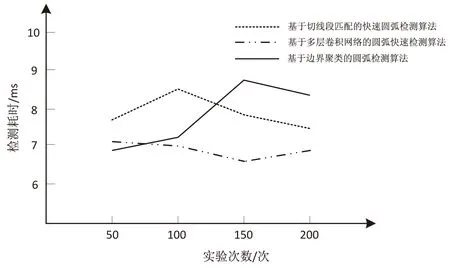
图7 不同圆弧检测算法检测耗时对比

分析图7可知，随着实验次数的不断增加，不同圆弧检测算法的检测耗时也相应发生变化。基于边界聚类的圆弧检测算法的检测耗时仅在最初时少于所提的基于多层卷积网络的圆弧快速检测算法，而基于切线段匹配的快速圆弧检测算法的检测耗时始终大于文中算法。对比结果表明，文中算法所用的检测时间最少。通过上述实验可知，所提圆弧检测算法的检测精度最高，因此可证明所提算法具有较高的检测效率。

3 结束语

基于多层卷积网络的圆弧快速检测算法通过圆弧信息聚类存储、圆弧全局聚类与获取圆弧阈值区间实现了圆弧快速检测，其检测速度高于传统圆弧检测算法，并且误检率远低于传统圆弧检测算法，实现了圆弧检测领域速度与效率的提升，对圆弧检测领域具有重大的意义。