缝合式C/SiC 复合材料非线性本构关系及断裂行为研究1)
曹明月 张 启 吴建国 葛敬冉 梁 军
(北京理工大学先进结构技术研究院,北京 100081)
(北京强度环境研究所可靠性与环境工程技术重点实验室,北京 100076)
引言
C/SiC 复合材料具有较高的比刚度、比强度及优良的高温性能,在航空航天等领域有广阔的应用前景[1-3].国内外学者针对C/SiC 复合材料的力学性能开展了广泛的试验研究[4-8],裂纹扩展进而引起的脆性断裂是其主要失效形式之一[9-10].C/SiC 复合材料服役于航空航天飞行器的发动机、机翼等多个部位,在材料的内部存在微小孔洞、微小裂纹等多种细观缺陷,在受到外来载荷的作用时,这些内部缺陷会进一步扩展形成宏观尺度上的裂纹,表现为基体/纤维开裂、界面脱粘等,最终可能会导致结构的破坏,极大地影响了材料的使用寿命.研究C/SiC 复合材料的断裂行为对改善材料性能有重要的意义,可以为结构设计和应用提供理论指导.
目前ABAQUS 中常用的模拟裂纹扩展的方法有节点释放技术[11-13]、内聚力单元法[14-16]和扩展有限元法[17-20]等.C/SiC 复合材料虽然是脆性材料,但却具有较好的韧性,外观表现出明显的非线性行为.单纯地使用ABAQUS 中的裂纹扩展方法不足以描述材料断裂失效前的非线性行为.建立材料的非线性损伤本构是描述其非线性力学行为的有效方法,目前针对C/SiC 类复合材料建立了多种本构方程[21-25].如Din等[21]基于PUCK 准则和热力学损伤演化定律开发了弹塑性损伤模型,可以描述开孔碳纤维增强聚合物层压板的非线性行为.Xie 等[22]提出了一个包含可变参数的塑性势函数,并基于Weibull 统计分布建立了损伤状态函数,所开发的本构模型能够计算3D 针刺C/C-SiC 复合材料在偏轴拉伸载荷以及剪切载荷下的力学响应.Li 等[23]引入标量型损伤变量,基于连续介质力学,提出了新的热力学势能函数,为C/SiC复合材料开发了一个弹塑性损伤本构,可以描述材料在循环载荷下的力学行为.Wei 等[24]基于PUCK 失效准则,引入两种剪切变形模式及缩放函数,开发了一个三维渐进损伤模型,可以描述拉伸载荷下大孔碳纤维增强聚合物板的3 种不同的破坏模式.杨正茂等[25]引入一组标量损伤变量,建立了陶瓷基复合材料含循环热冲击预损伤材料的损伤演化模型,可以描述陶瓷基复合材料在热机械载荷作用下的损伤演化特征.国内外学者在C/SiC 类复合材料非线性本构方程上取得了重要的成果,但大都参数确定复杂.针对缝合式C/SiC 复合材料可用于断裂计算的非线性本构方程还鲜有涉及.
本文为模拟缝合式C/SiC 复合材料单边切口梁和双悬臂梁的断裂行为,基于简单力学试验和CT 扫描结果,建立了宏观非线性损伤本构方程.在有限元软件ABAQUS 中,将非线性本构方程编写成UMAT子程序,应用到简单算例中,验证本构方程有效性.进而模拟缝合式C/SiC 复合材料单边切口梁和双悬臂梁断裂的力学响应,与试验结果进行对比.为缝合式C/SiC 复合材料的结构设计和进一步应用提供理论基础.
1 缝合式C/SiC 复合材料力学试验
1.1 基础力学试验
缝合式C/SiC 复合材料,在原有二维平纹编织C/SiC 复合材料的基础上,在厚度方向上引入了纱线缝合[26],采用CVI[27]工艺制备而成.其在不同的加载条件下表现出不同的力学特性,但基础载荷状况是拉伸、压缩、剪切.拉伸试验件参考标准ASTM C1275—2000.压缩试验件参考标准ASTM C1358—2005.剪切试验件参考标准ASTM C1292—2000(2005).每种工况做3 个试验件.
通过试验,获得了0◦正轴向试件的平均拉伸、压缩和剪切应力−应变曲线.由图1(a)可以看出缝合式C/SiC 复合材料从开始加载就表现出明显的非线性特征,模量随应变的增大而减小.图1(b)显示在压缩载荷下,材料表现出准脆性材料的力学行为.失效前应力−应变曲线表现为近线性,且压缩强度高于拉伸强度,反映出材料的损伤行为具有显著的拉压异性特征.由图1(c)可以看出,在剪切载荷下材料也表现出明显的非线性.C/SiC 材料内部存在大量微孔洞,在加载过程中,微细观损伤产生并累计,宏观表现为刚度退化和非弹性应变的累积,最终导致材料表现出非线性特征.
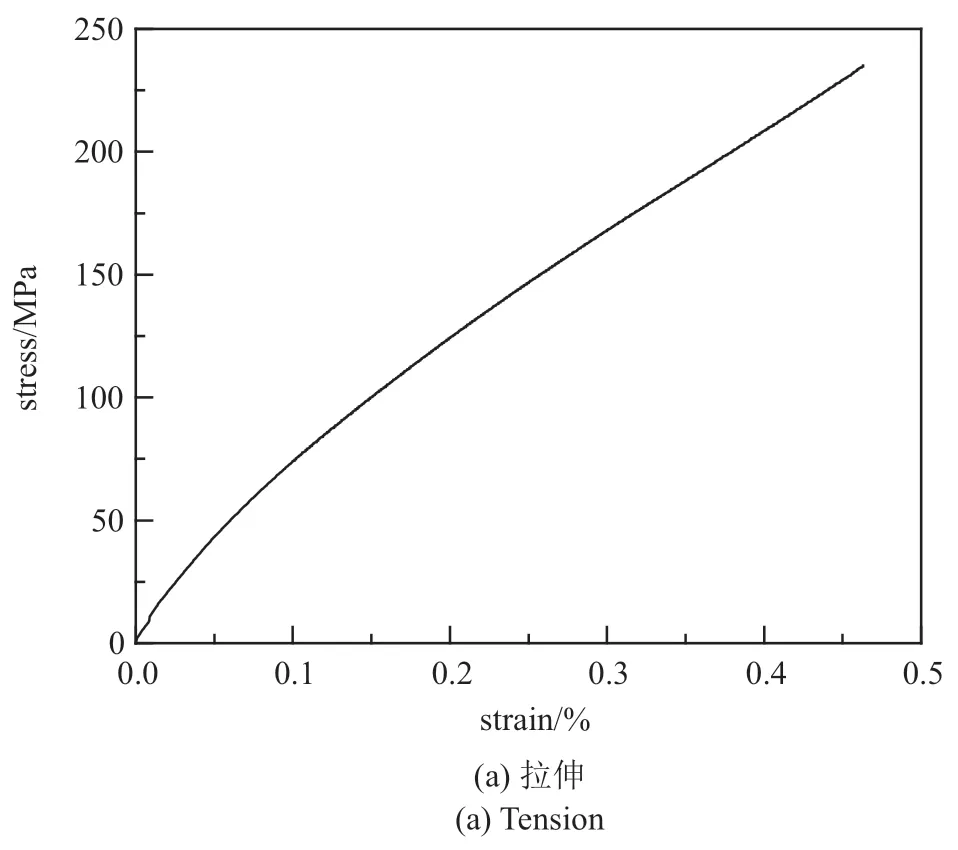
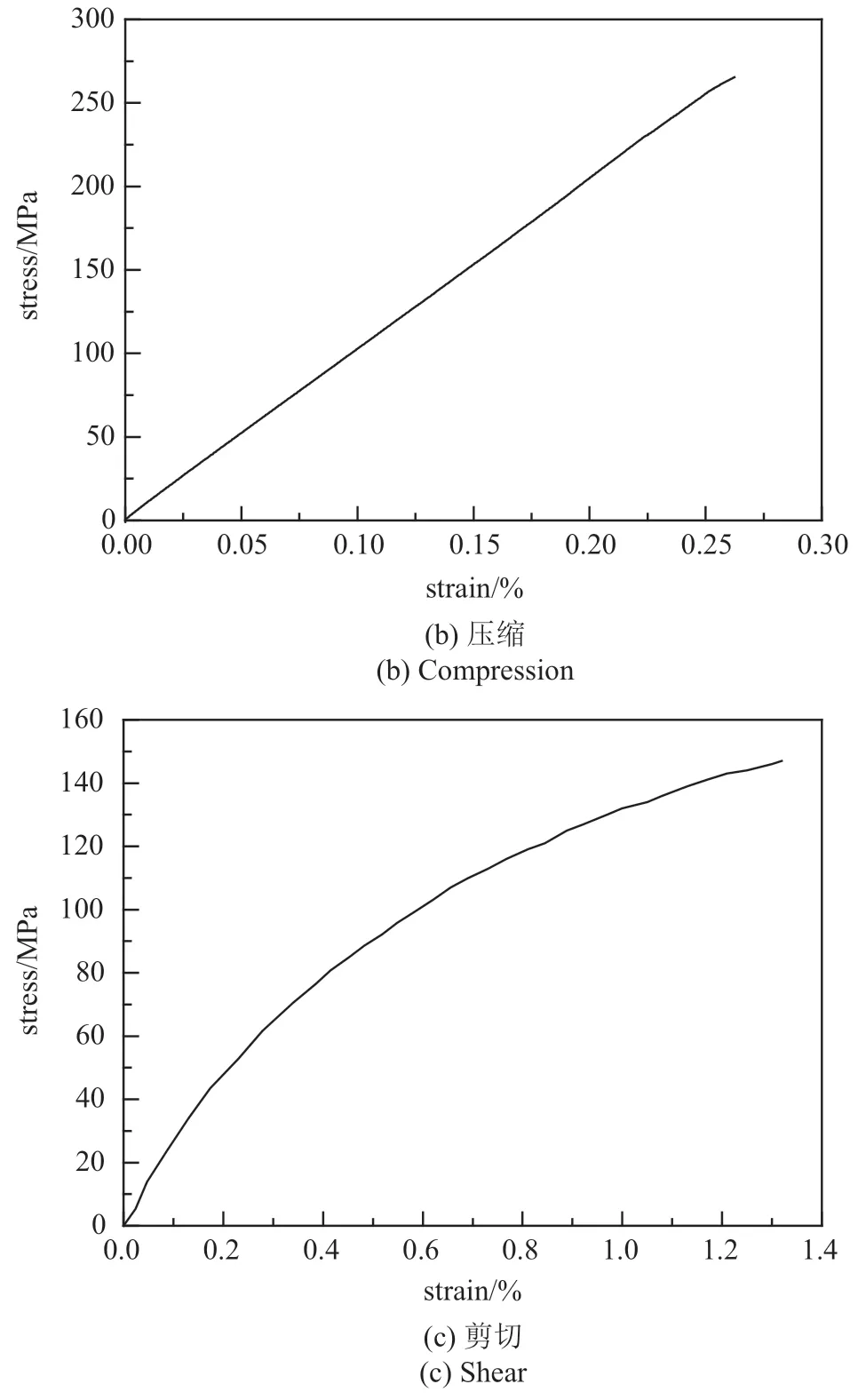
图1 基础力学试验曲线Fig.1 Experimental curve of basic mechanics
缝合式C/SiC 复合材料的细观结构包括纤维束、基体和初始缺陷.以拉伸为例,由图2 拉伸试件的CT扫描结果可以看出,基体中裂纹数量和缺陷面积远远大于纤维束中的裂纹数量和缺陷面积.这可能是由于材料承受拉伸载荷时,基体强度小于纤维束强度,基体所受应力先达到开裂应力,基体中缺陷萌生裂纹,随着拉伸载荷的不断增大,最终出现图2 中的纤维开裂和界面脱粘现象.在此过程中的微细观损伤的产生和累计是导致材料非线性的主要原因.

图2 拉伸应力下CT 扫描照片Fig.2 CT scan photos under tensile stress
1.2 单边切口梁试验
采用单边切口梁法 (SENB),对缝合式 C/SiC复合材料的面内断裂性能进行测试,测试标准参考ASTM E399-17.如图 3 所示,设计试样尺寸为30 mm×6 mm×3.5 mm,裂纹长度为3 mm,宽度为0.5 mm,实验加载速度为0.1 mm/min.共做3 个试验件.
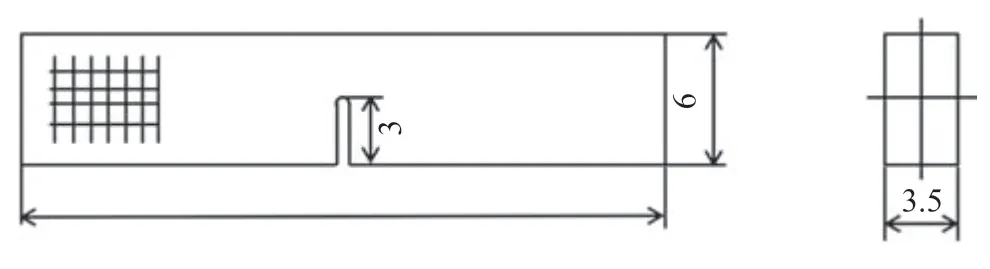
图3 单边切口梁(SENB)试件Fig.3 Single side notched beam(SENB)test piece
单边切口梁平均力−位移曲线如图4 所示,力−位移曲线初始阶段有上凸尾迹存在,这是由于夹具与试样件之间的滑移.之后曲线呈现近似线性变化.在接近最大载荷前,有一小段曲线表现出短暂的非线性,这可能是由于部分纤维断裂造成的.达到最大载荷之后,曲线呈现波动下降特征,这可能是由于纤维趋向于相对较小的聚集状态,有层次地发生断裂拔出.图4 中展示了单边切口梁试件破坏后的宏观形貌,材料在试验前后几何外观并没有发生明显的形变,未发现明显的裂纹扩展现象.
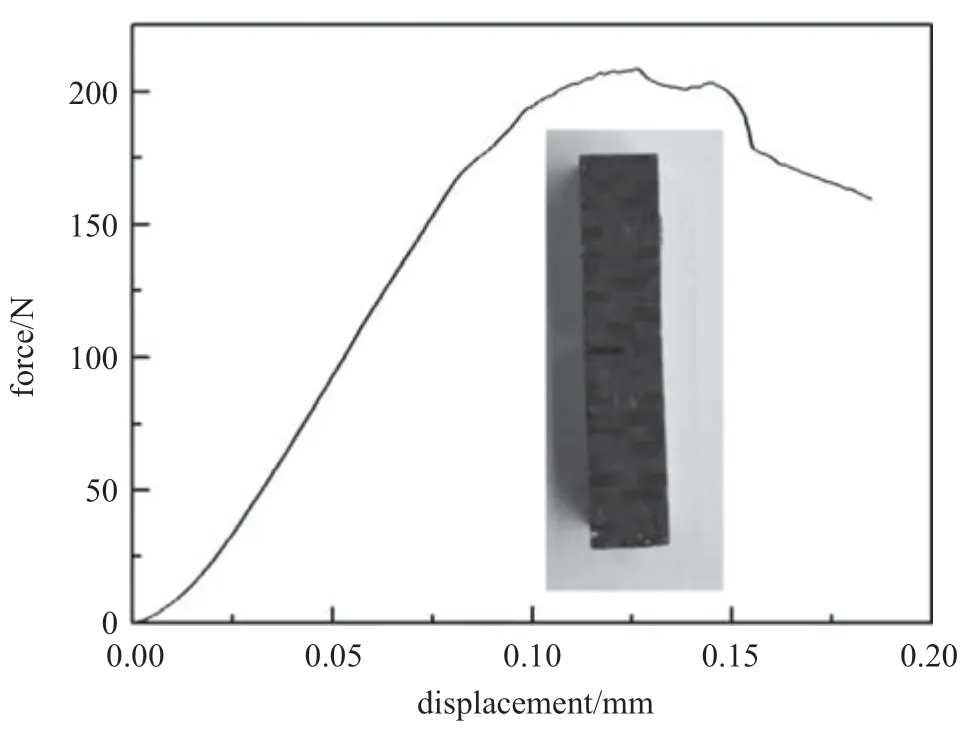
图4 单边切口梁力−位移曲线Fig.4 Force-displacement curve of single-sided notched beam
1.3 双悬臂梁试验
采用双悬臂梁试验,对缝合式C/SiC 复合材料的层间断裂性能进行测试,测试标准参考ASTM D5528.设计试样尺寸为170 mm×20 mm×6 mm,初始裂纹长度98 mm,缝宽为0.79 mm,如图5 所示.共做3 个试验件.
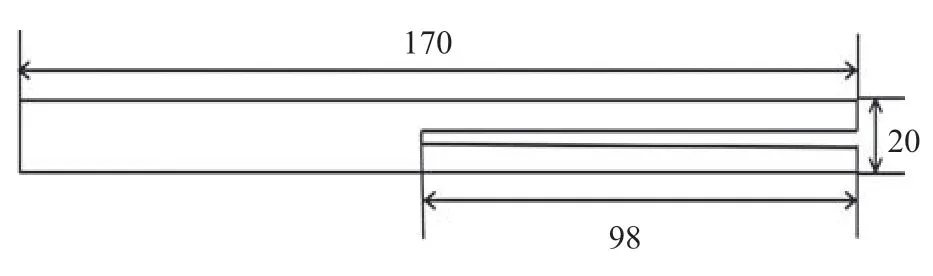
图5 双悬臂梁试件Fig.5 Double cantilever beam test piece
双悬臂梁平均力−位移曲线如图6 所示,由曲线可以看出材料在失效前表现出一定的非线性.在图中从左到右出现4 个突降点.第一个突降点是由加工问题导致,在试验件宽度中部产生了小面积的裂纹扩展;第二个突降点对应的是力的最大值,该时刻试验件边缘裂纹初次扩展;第三个突降点对应试验件边缘的裂纹第二次较大扩展;第四个突降点处,裂纹已经缓慢扩展至最大值,停止扩展,并开始逐渐弯曲破坏.图6 中展示了双悬臂梁试件破坏后的宏观形貌,可以看出层间裂纹扩展了较大距离.

图6 双悬臂梁力−位移曲线Fig.6 Force-displacement curve of double cantilever beam
2 宏观非线性损伤本构
缝合式C/SiC 复合材料在加载状态和卸载状态下有不同的应力−应变曲线.以沿材料主方向上的拉伸加卸载下的应力−应变曲线为例进行分析,忽略迟滞效应的影响,可以得到一个理论化的模型,如图7所示.
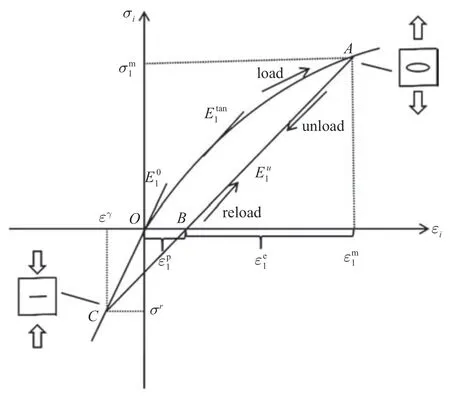
图7 拉伸加卸载材料的应力−应变曲线图[28]Fig.7 Stress-strain curve of materials under tension loading and unloading[28]
假设材料首先历经OA段承受拉伸载荷的过程,对应A点的应力和应变.图中表示材料主方向上(1 方向)的拉伸弹性模量,为拉伸加载条件下的切线模量,表示卸载(或重新加载至卸载点前)阶段的卸载模量.模型中假设C点(εr,σr)为“裂纹闭合点”,随着拉伸加载应力不断增大,由于部分残余应力释放,该裂纹闭合点的应力值会发生一定的变化.
从O点开始对材料进行加载,初始模量为,在拉伸载荷超过弹性极限后,由于材料中产生基体开裂、界面脱粘等微观损伤,材料的拉伸切线模量随加载应力的增大而不断减小,并形成非弹性应变.加载至A点后经历卸载过程,卸载路径近似沿A点至B点所在直线,卸载模量小于弹性模量.当拉伸应力向压缩应力状态转换后,由于基体微裂纹闭合等原因,卸载模量在较高的压缩应力水平下近似恢复到初始弹性模量,即表现出损伤钝化行为.假设压缩应力超过σr后,卸载模量完全恢复为初始弹性模量.重加载时应力−应变路径则沿C点至A点所在直线,过A点后再加载将产生新的拉伸损伤,切线模量和卸载模量继续减小,直至材料最终破坏.面内剪切加卸载条件下,材料的应力−应变曲线形态与拉伸试验结果类似,但是剪应力反向后不存在“裂纹闭合点”.
以上分析表明,材料在拉伸或剪切载荷下,加载历史对力学行为有很大影响.因此,本构模型中描述复合材料的应力−应变行为时,应把材料所经历的加载历史作为一个考虑点,并区分加载和卸载两种不同状态下的应力−应变关系.基于以上分析,本文参考二维C/SiC 复合材料的本构方程[28-30],建立了缝合式C/SiC 复合材料的非线性损伤本构方程.
2.1 非线性应力应变关系
缝合式C/SiC 复合材料的预制体为周期性平纹编织结构,可将其视为正交各向异性材料,其应力−应变关系为

其中,εi和σi(i=1,2,6)分别为材料主方向和剪切方向的应力和应变,依次为初始弹性模量、剪切模量、泊松比.S0为无损伤状态下的柔度矩阵.
在加载过程中,缝合式C/SiC 复合材料产生损伤,模量、泊松比等性质都会有所变化,但损伤后的材料仍可近似视为正交各向异性材料.由于数值非常小,可以近似视为常数,同时满足.据此对式(1)求逆,得到损伤后材料应力−应变关系的增量表达式

式中,t=,C为损伤后材料的刚度矩阵.E1,E2和G12为损伤后材料的拉伸模量和剪切模量,随着加载状态的改变而改变,可以描述材料的加卸载损伤状态.
由于缝合式C/SiC 复合材料卸载存在残余应变,表现出伪塑性行为;加载过程中材料模量逐渐减小.用函数[29]描述单调加载条件下材料的拉伸和剪切应力−应变关系
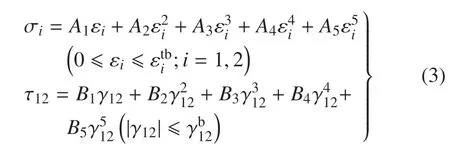
式中,Ai和Bi(i=1,2,...,5)为多项式函数的第i阶系数;为材料的拉伸断裂应变,为面内剪切断裂应变.
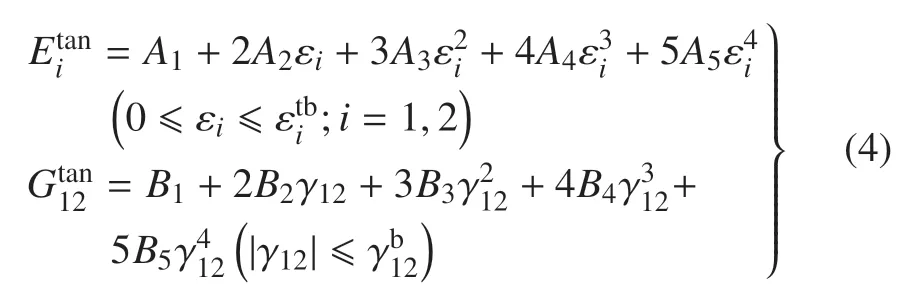
式中,A1和B1的物理意义即为材料的拉伸和剪切初始弹性模量.
材料压缩试验曲线中,应力−应变曲线表示为近线性,因此描述压缩状态下的应力−应变关系函数为


式中,A7,A6,y0和e0为逻辑函数的形状参数,由实验曲线拟合得到.σr为裂纹闭合点应力,为面内简单拉伸加载所达到的最大拉伸应变.当无加载历史(即=0)时,=A7.参数A7的物理意义为拉伸弹性模量.
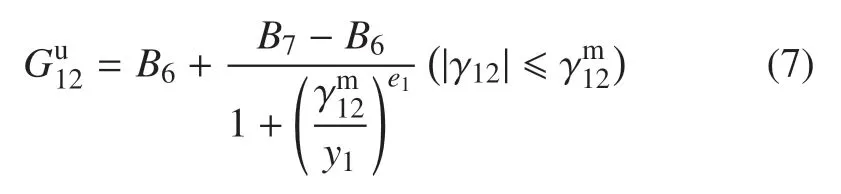
式中,B7,B6,y1和e1为形状参数,由实验曲线拟合得到.
目前国内外尚且没有统一的有关复合材料的失效准则,本文采用考虑材料拉压强度不等的Hoffman失效准则[31-32],其表达式如下
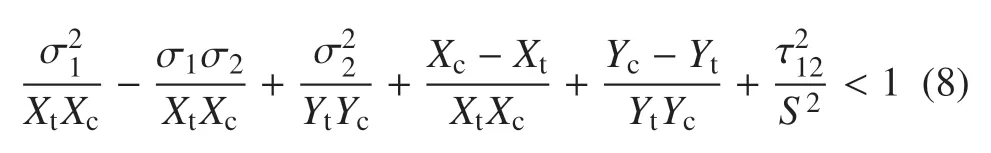
式中,Xt和Yt分别为1 方向和2 方向的拉伸强度,Xc和Yc非别为1 方向和2 方向的压缩强度,S为剪切强度.非线性本构方程中所使用的参数如表1 所示.
表1 中A6,A7,y0,e0,B6,B7,y1,e1这8 个和卸载相关的参数参考文献[5]的实验数据.
2.2 数值实现
将非线性损伤本构模型编写成用户材料子程序UMAT.为了更好地收敛,需要计算材料的雅克比矩阵D,即应力增量对应变增量的变化率.其定义如下

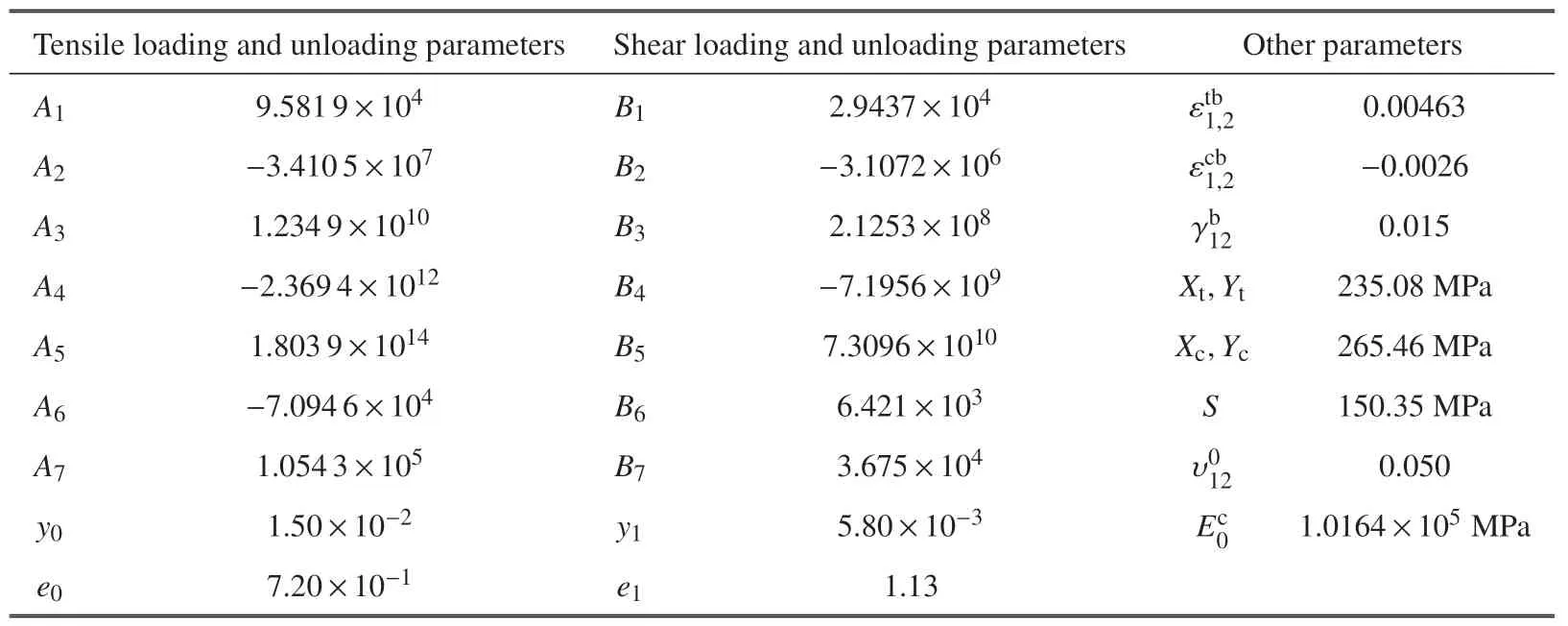
表1 缝合C/SiC 复合材料本构模型参数Table 1 Parameters of stitched C/SiC composites constitutive model
当增量步的步长足够小,即∆t→0 时,根据式(2),近似有
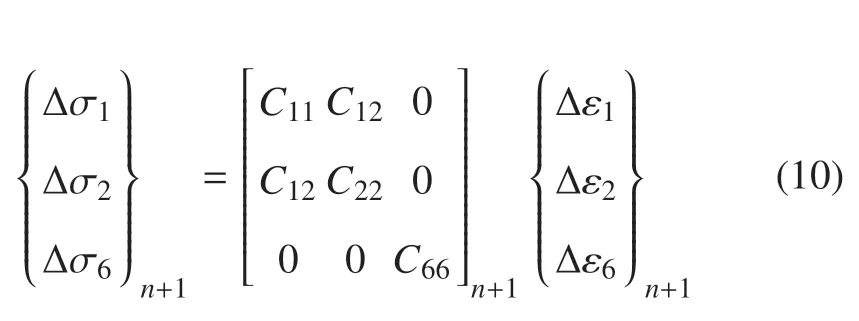
(1)读取n+1 步的应变张量εn+1=εn+∆εn+1;
(2)判断加卸载状态εi,n+1⇔,σi,n⇔σr;
(3)计算损伤模量E1,E2,G12;
(4)计算名义应力张量 {σi}n+1={σi}n+;
(5)计算雅可比矩阵D=;
(6)失效判断.
2.3 单个单元验证
在ABAQUS 中建立单个单元模型,单元类型选取4 节点减缩积分平面应力单元(CPS4R),结合UMAT 模拟简单加载条件下缝合式C/SiC 复合材料的力学响应,如图8 所示.由图8 可以看出,模拟结果与试验结果吻合良好.图8 中,压缩强度在达到破坏强度以前,先满足了UMAT 中使用的Hoffman 失效判据,所以试验压缩强度大于模拟压缩强度.剪切则与之相反,所以试验剪切强度小于模拟剪切强度.综上,本文建立的本构方程可以很好地描述缝合式C/SiC 复合材料的非线性.
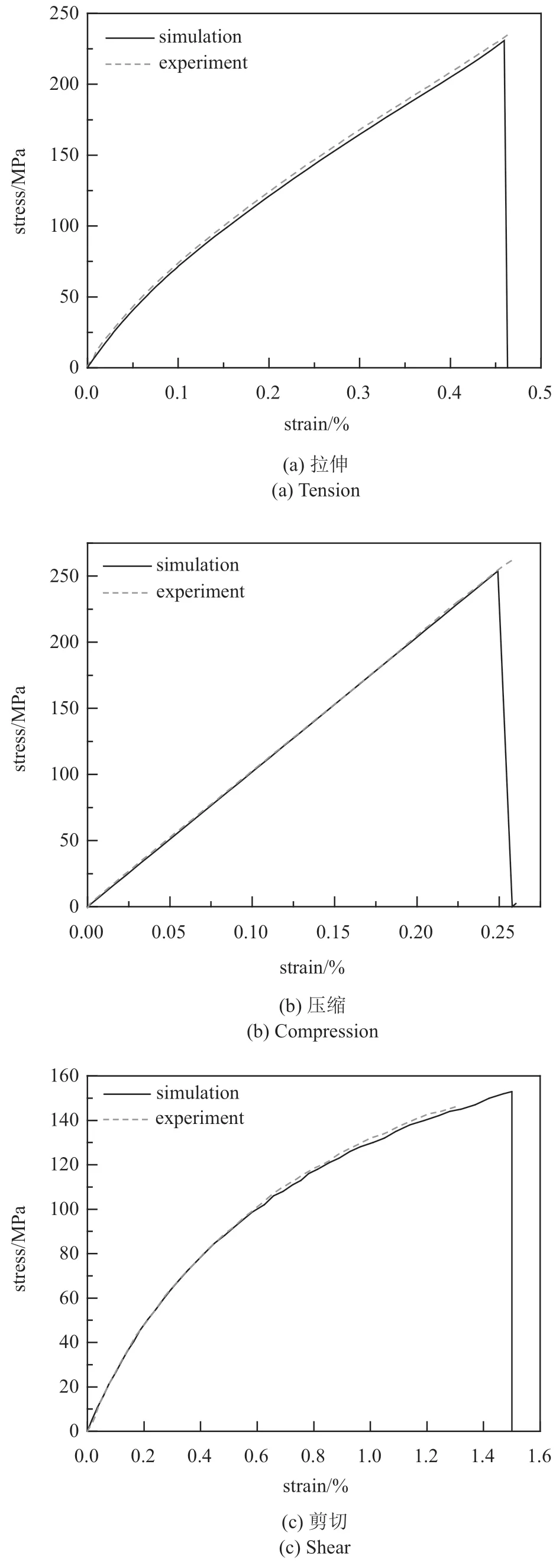
图8 简单加载下材料的应力−应变曲线对比图Fig.8 Comparison of stress-strain curves of materials under simple loading

图9 复杂应力下材料的应力−应变曲线图Fig.9 Stress-strain curve of materials under complex stress
同样,在ABAQUS 中建立单个单元模型,结合UMAT 模拟复杂应力状态下缝合式C/SiC 复合材料的力学响应,如图9 所示.由图9(a)和图9(b)可以看出,加载模量随应变增大而减小,卸载模量随应变的增大而减小,残余应变越来越大,材料具有明显的非线性特征,表现出伪塑性.由图9(c)可以看出,反向加载到一定程度时裂纹闭合,材料模量恢复成初始模量.当材料加载载荷达到相应的破坏强度时,刚度矩阵取接近于零的数值,模拟材料的破坏.基于以上分析,建立的非线性本构方程可以模拟重复使用下材料的力学行为,为缝合式C/SiC 复合材料结构的进一步应用提供借鉴.
3 缝合式C/SiC 复合材料断裂行为模拟
3.1 单边切口梁断裂行为模拟
依据1.2 节单边切口梁试件,建立如图10(a)所示的模型,单元类型为CPS4R,模型共有21 951 个网格,为验证网格无关性,同时计算了所示模型1/4,1/2,2 倍网格数量的模型,综合考虑计算效率和精度,选择了目前的模型.边界条件如图10(a)所示,两个支座和压头均为刚体,在刚体和单边切口梁之间建立面面接触,固定左右两个支座起支撑作用,上方的压头施加向下的位移载荷.并对裂纹周围的网格进行加密,以便更好地捕捉断裂行为.
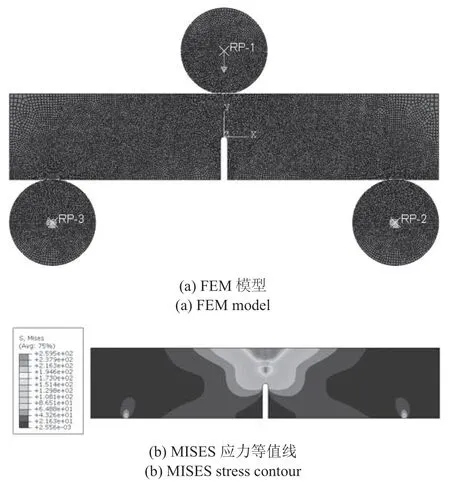
图10 单边切口梁模型Fig.10 Single-sided notched beam model
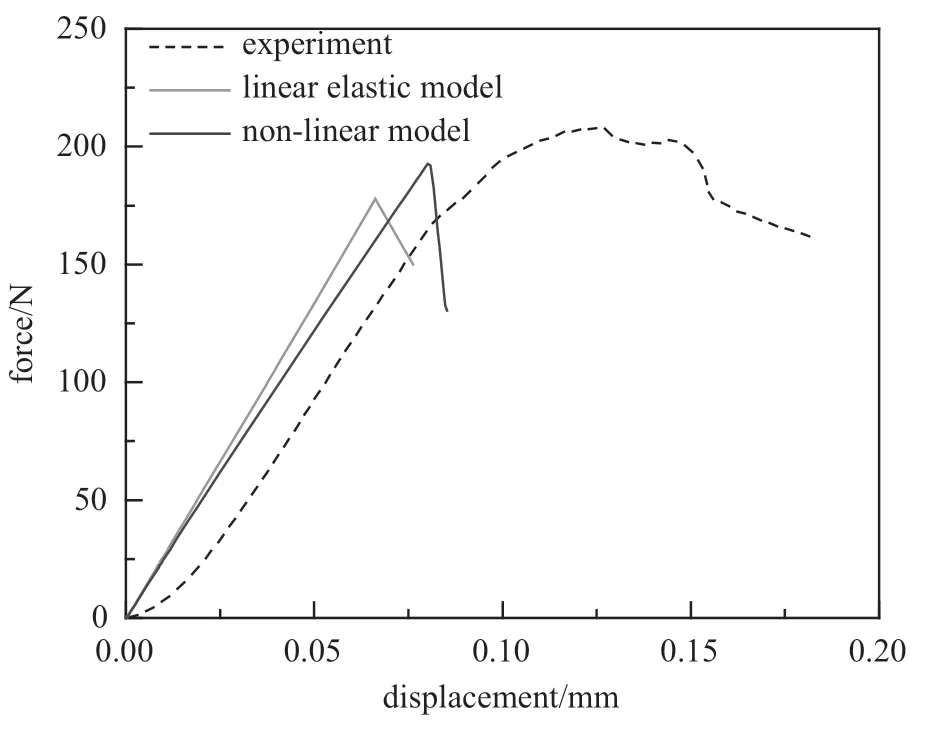
图11 单边切口梁模拟与实验结果对比图Fig.11 Comparison of simulation and experimental results of single-sided notched beam
结合第2 节所述宏观非线性本构的UMAT 子程序进行模拟,同时对比计算了线弹性本构下的单边切口梁断裂行为.使用非线性模型计算得到的单边切口梁MISES 应力云图如图10(b)所示,数值计算结果同试验结果对比如图11 所示.由图11 看出,强度点前,试验与模拟曲线接近平行却没有重合,是由于SENB 试验中,夹具与试样件之间滑移导致上凸尾迹,线弹性模型没有考虑材料的非线性行为,所以更加偏离试验曲线.强度点后,试验与模拟结果存在一定差异,是由于有限元模型对实际模型进行了简化,没有区分出纤维和基体,没有考虑缝合纱位置,而基体纤维相继失效和缝合纱位置对强度点后的试验曲线有较大的影响.由表2 可以看出,线弹性模型预测的失效载荷相对试验失效载荷误差为−14.625%,而非线性模型误差为−7.448%,线弹性模型的失效载荷误差是非线性模型的1.96 倍,非线性模型计算结果与实验结果较为接近.

表2 单边切口梁有限元与实验结果的比较Table 2 Comparison of finite element and experimental results of single-sided notched beam
3.2 双悬臂梁断裂行为模拟
依据1.3 节双悬臂梁试验,建立如图12(a)所示的模型,单元类型为CPS4R,模型共有17 590 个网格,为验证网格无关性,同时计算了所示模型1/4,1/2,2倍网格数量的模型,综合考虑计算效率和精度,选择了目前的模型.采用在左端固定,在裂缝上下两侧施加位移载荷的边界条件,如图12(a)所示.对裂纹周边的网格进行加密.

图12 双悬臂梁模型Fig.12 Double cantilever beam model
结合第2 节所述宏观非线性本构的UMAT 子程序进行模拟,同时对比计算了线弹性本构下的双悬臂梁断裂行为.使用非线性模型计算得到的双悬臂梁MISES 应力云图如图12(b)所示,数值计算结果同试验结果对比如图13 所示.由图13 看出,强度点前,非线性模型曲线与实验曲线较为接近,线弹性模型与实验曲线相差较大,是由于线弹性模型没有考虑材料的非线性行为.强度点后,试验与模拟结果存在一定差异,是由于有限元模型对实际模型进行了简化,没有区分出纤维和基体,没有考虑缝合纱的位置,而基体纤维相继失效和缝合纱位置对强度点后的试验曲线有较大的影响.由表3 可以看出,线弹性模型预测的失效载荷相对试验失效载荷误差为15.926%,而非线性模型误差为4.244%,线弹性模型的失效载荷误差是非线性模型的3.75 倍,非线性模型计算结果与实验结果较为接近.本文提出的计算模型可以较好地模拟缝合式C/SiC 复合材料的力−位移曲线.

图13 双悬臂梁模拟与试验结果对比图Fig.13 Comparison of simulation and test results of double cantilever beam

表3 双悬壁梁有限元与实验结果的比较Table 3 Comparison of finite element and experimental results of double cantilever beams
4 结论
(1)本文依据简单力学试验及CT 扫描结果,为缝合式C/SiC 复合材料建立了宏观非线性本构方程.本构方程中参数可以通过数量较少的简单加载及加卸载力学试验获得.本构方程可以区别加载、卸载、重加载三种状态,并考虑了反向加载过程中造成的裂纹闭合,可以描述缝合式C/SiC 复合材料在复杂应力状态下的力学行为.
(2)在ABAQUS 中,结合UMAT 模拟缝合式C/SiC 复合材料单边切口梁和双悬臂梁的断裂行为.与线弹性本构对比,非线性本构模拟结果与试验更加吻合.说明本文建立的非线性本构可以较好地预测缝合式C/SiC 复合材料单边切口梁和双悬臂梁的断裂行为.
(3)本文基于简单力学试验建立了缝合式C/SiC复合材料的宏观唯象本构方程,未区分纤维、基体和缺陷,在后续工作中将建立复合材料的细观模型,把孔隙作为单独的因素考虑,结合现有宏观模型,实现对C/SiC 复合材料的多尺度分析.

