柔性铰柔性杆机器人动力学建模、仿真和控制1)

方五益 郭 晛 黎 亮 章定国

(南京理工大学理学院,南京 210094)

引言

空间机械臂[1]是一种强耦合、高度非线性的复杂柔性多体系统.而关节柔性和臂杆柔性的客观存在是引起空间机械臂振动的根本原因,因此柔性铰柔性杆机器人的研究具有实际工程意义.

对于柔性杆件的研究,Likins[2]用混合坐标法建立柔性多体动力学零次近似刚柔耦合模型.Book[3]采用假设模态法表示杆件的弹性变形,借助于齐次变换矩阵,推导出递推形式的多杆柔性机械臂系统的拉格朗日动力学方程.章定国[4]在Book 的研究基础上,考虑了杆件的扭转效应,优化了递推过程,并给出了仿真算例.洪嘉振等[5]从连续介质力学的基本原理出发,建立了一次近似刚柔耦合动力学模型,并通过实验验证其正确性.文献[6～9]运用一次近似刚柔耦合模型对柔性梁进行了相关研究.陈思佳等[10]保留一次近似耦合模型中耦合变形量的高阶项,建立了更精确的高次刚柔耦合动力学模型.最近几年,吴吉等[11]用绝对节点坐标法研究了带集中质量的旋转柔性曲梁动力学特性.范纪华等[12]用绝对节点坐标法对柔性单摆的动力学问题进行研究.另外,范纪华等[13]对旋转中心刚体−功能梯度材料梁刚柔热耦合动力学特性进行了研究.

关于柔性关节的研究,Spong[14]将柔性关节简化为线性扭转弹簧模型.Bridges 等[15]考虑了摩擦、柔性非线性和运动误差等,提出了更精确的关节模型.周胜丰等[16]用Kane 方法推导出柔性多杆多铰机器人动力学方程,通过仿真算例说明铰的柔性不可忽略.刘俊[17]用递推拉格朗日方法推导出柔性多杆多铰机器人刚柔耦合动力学方程,方程中还考虑了铰的质量效应和扭转变形.范纪华等[18]研究了关节柔性对机器人动力学的影响.Xi 等[19]建立了由单根柔性杆和单个柔性铰组成的全柔机器人的动力学模型,且研究了柔性杆与柔性铰之间的耦合关系.边枢宇[20]基于Kane 法建立了多杆全柔机器人的动力学方程,并通过单杆全柔机器人的仿真算例说明杆柔性与关节柔性对机器人动力学响应的影响.Al-Bedoor 等[21]建立了末端带有载荷的单杆全柔机器人的动力学模型.Zhang 等[22]建立了多个柔性杆和柔性铰并存的空间全柔机器人的动力学模型,模型中考虑了柔性杆件的弯曲、扭转和拉伸变形.Qian 等[23]详细推导了空间全柔机器人的动力学模型,并开发了多杆机械臂的通用软件包.陈思佳等[24]推导了带杆端集中质量的柔性单杆单铰机器人高次刚柔耦合动力学方程,并进行了仿真分析.

为保证复杂系统的动力学方程得以高效高精度的求解,诸多学者们对于柔性多体系统动力学的数值积分方法也进行了相关研究.如芮筱亭等[25]对柔性多体系统动力学建模理论和数值求解方法都进行了研究.郭晛等[26]对柔性多体系统动力学的数值积分方法进行了研究.

对于空间机械臂动力学控制的研究,与逆动力学求解息息相关.Guaraci[27]详细介绍并讨论了欠驱动机械臂前馈控制的逆动力学方法.Krzysztf[28]提出了一种基于逆动力学的柔性铰机器人的非线性反馈控制方法.Jankowski[29]使用柔性铰机器人动力学模型,提出了一种基于逆动力学的离散控制方法.

以上关于柔性铰机器人的研究,暂未考虑铰阻尼的存在.在太空中,空间机械臂发生振动后,需要很长时间才能恢复到稳定的状态.此时铰阻尼的存在可使系统快速稳定下来,因此铰阻尼的研究具有工程意义.本文采用递推拉格朗日方法,推导出考虑铰阻尼的柔性机器人刚柔耦合动力学方程,研究铰的柔性对机器人动力学响应和动力学控制的影响,以期为柔性机器人的减振与控制提供参考.

1 柔性铰柔性杆机器人的动力学建模

1.1 柔性铰柔性杆机器人的物理模型

柔性铰柔性杆机器人是由n个铰和n根杆件组成的空间链式多体系统,如图1 所示.

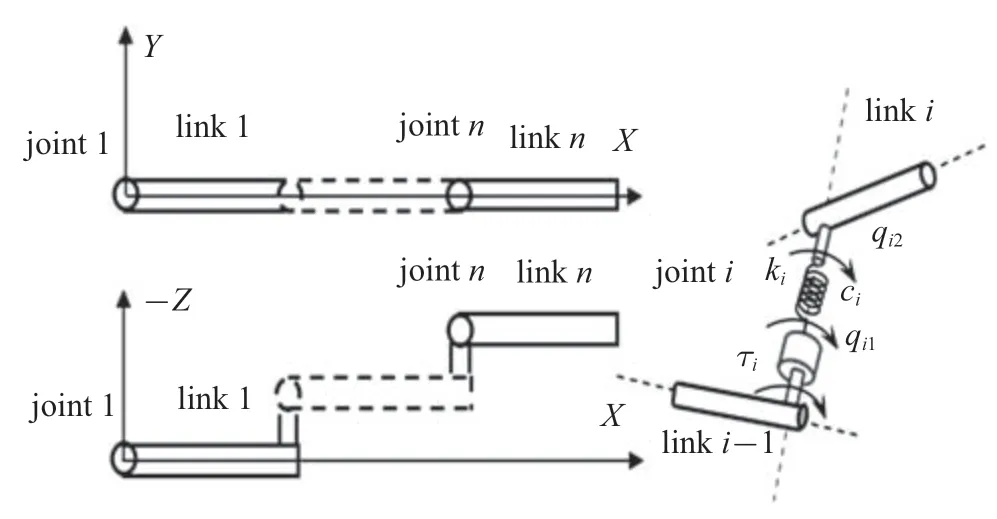
图1 柔性铰柔性杆机器人Fig.1 The robot with flexible joints and flexible links

柔性杆模型基于Euler-Bernoulli 梁,变形处于线弹性阶段.模型中考虑了杆件拉压、弯曲变形和扭转变形.柔性铰模型基于Spong 的柔性关节简化模型,将柔性铰看成线性扭转弹簧,并考虑铰阻尼的存在.τi为铰i的驱动力矩,ki为铰i扭转刚度系数,ci为铰i阻尼系数,qi1为铰i驱动装置的角位移,qi2为铰i传到杆件i的角位移.qi2−qi1为铰柔性引起的扭转变形.

1.2 柔性机器人的运动学描述

在建模过程中,引入齐次坐标和齐次变换矩阵来描述杆件的位置和姿态.为清楚表示各坐标系之间的转换关系,在i杆的近端和远端各建立两个正交坐标系:坐标系(XbYbZb)i固定在i杆的近端,沿Xb沿杆件i未变形时的中性轴;坐标系(XdYdZd)i固定在i杆的远端,在杆i未变形时,(XdYdZd)i看作是(XbYbZb)i沿杆件i的轴线方向平移杆件i的长度Li而成;坐标系(HxHyHz)i固定在i杆件的远端,z轴沿着关节的转轴;坐标系固定在杆件i的近端,铰i未动时,与(HxHyHz)i−1重合.可见,坐标系(XdYdZd)i与坐标系(HxHyHz)i之间的4×4齐次变换矩阵dHi是一个常数阵,坐标系(HxHyHz)i与(XbYbZb)i之间的变换矩阵Hbi也是一个常数阵,与(HxHyHz)i−1之间的变换矩阵只是铰i铰变量qi2的函数.

定义铰i的变换矩阵为Ai,即从坐标系(Xd Yd Zd)i−1到坐标系(Xb Yb Zb)i的变换矩阵,则

定义Ei是杆件i的变形变换矩阵,即从坐标系(XbYbZb)i到杆件i变形后的坐标系(XdYdZd)i的变换矩阵.由于杆件i的变形是基于小变形假设,故Ei可近似表达为

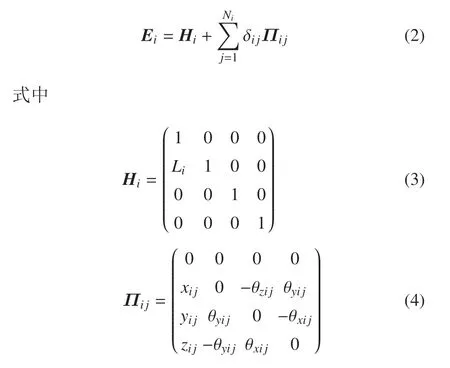
其中,xij,yij,zij分别是杆件i的第j变形线位移模态在坐标系(XbYbZb)i的三轴上的分量;θxij,θyij,θzij分别是杆件i的第j变形角位移模态在坐标系(XbYbZb)i的三轴上的分量;δij是杆件i的第j个模态坐标;Ni是杆件i的模态数.

令Wi是基座坐标系(XbYbZb)0到(XbYbZb)i之间的齐次变换矩阵,则

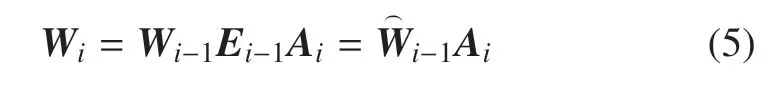
采用假设模态法描述杆件的变形,考虑由杆件横向变形引起的纵向耦合变形.杆i上某点P(η,0,0)变形后在连体坐标系中的齐次坐标ihi为

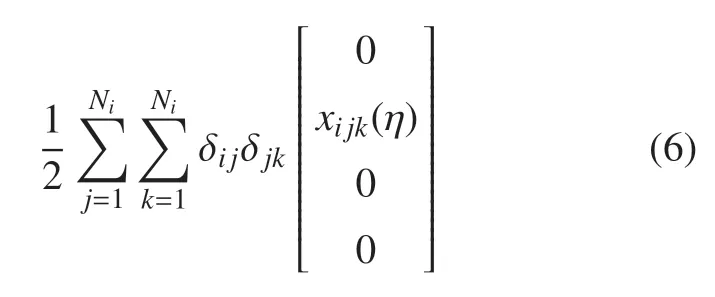
式中,xijk(η)是采用非线性应变场产生的高阶耦合项,与传统零次动力学模型不同,考虑了该项的高次刚柔耦合动力学模型能够捕捉到大范围运动与变形的相互影响,所得结果更加精确.xijk(η)可表示为

该点在基座坐标系中的齐次坐标hi可以表示为

将hi对时间求导,可以得到该点的速度为

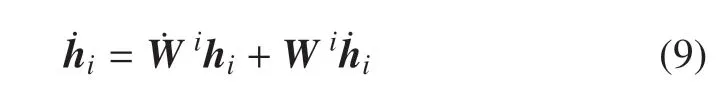
1.3 系统的动能和势能

系统的动能包括杆的动能和铰的动能.杆i的动能可表示为

上式中,Li为杆i长度,µi为柔性杆单位长度质量,Tr(·)表示对括号中的矩阵求迹,Jxi为杆i绕xi轴单位长度转动惯量,θxi为杆i绕xi轴扭转角.式(10)中,右边的第一项为杆件大范围运动、纵向拉压变形运动和横向弯曲变形运动引起的动能,第二项为杆件扭转变形运动引起的动能.其中,θxi可表示为

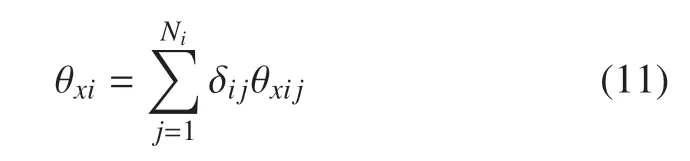
柔性铰i的动能分为平动动能和转动动能.对于平动动能,把铰i看作杆i靠近铰i端的集中质量计入杆的动能.而柔性铰i的转动动能可表示为

式中,Jri为铰i转动惯量,φi是转子的角位移,经过齿轮变速后输出角位移qi1到柔性铰上,因此qi1=φi/ni,其中ni为齿轮传动比.于是式(12)可表示为

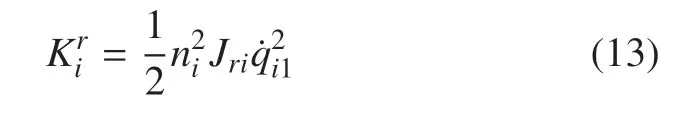
综上,系统的总动能为

系统的势能包括柔性杆和柔性铰的弹性变形势能以及它们的重力势能.柔性杆i的弹性势能包括拉压变形势能、弯曲变形势能、扭转变形势能

其中,Ei是杆i的杨氏模量,Gi是杆i的剪切模量,Axi是杆i的横截面积,Ixi是杆i横截面关于中性轴的极面积惯性矩,Iyi和Izi是杆i横截面关于yi和zi轴的面积惯性矩,θyi和θzi为杆i绕yi和zi轴转角.θxi如式(11)所示,θyi,θzi可表示为

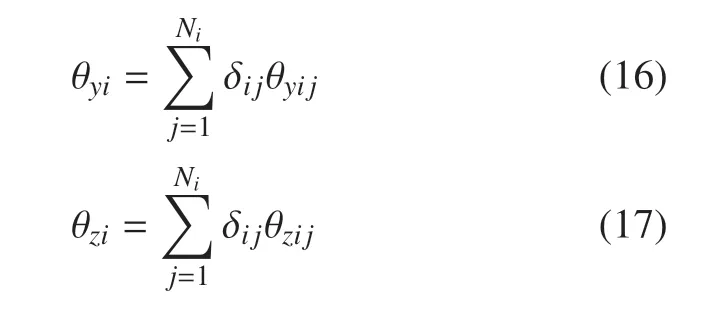
xi为杆件i的拉压变形,可表示为

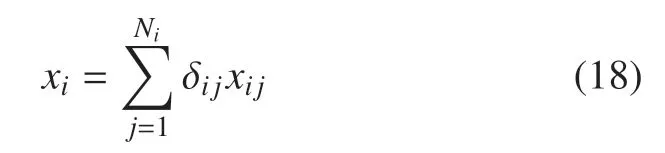
柔性铰i的弹性势能为

系统的弹性势能为

系统的重力势能为

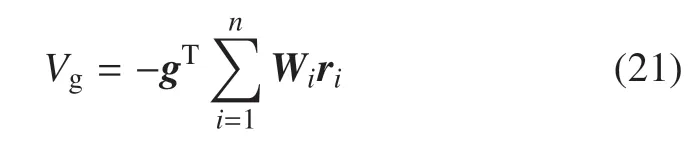
其中,g为重力加速度阵,ri为杆i质心位置矩阵,其具体形式见参考文献[23].于是系统的总势能为

1.4 系统的动力学方程

取广义坐标

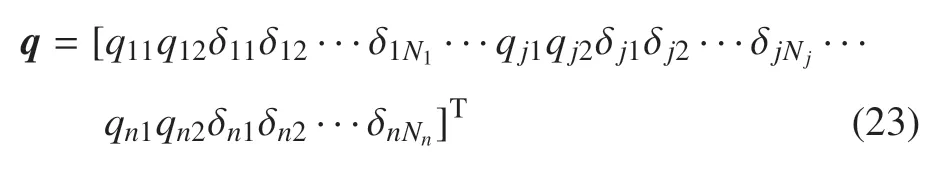
将系统的动能(14)和势能(22)代入到第二类拉格朗日方程

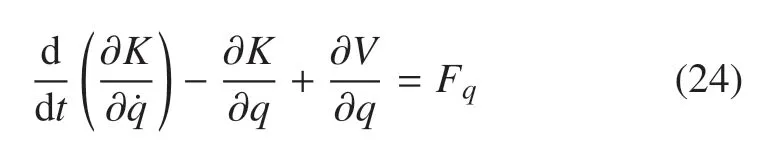
得到系统的动力学方程组为

以上得到的方程为考虑铰阻尼的柔性杆柔性铰机器人刚柔耦合动力学方程,其中的相关变量可以参看文献[6-7,17,23].双下划线部分为考虑铰阻尼时产生项,该项会使系统的动力学响应衰减.以上方程最终可整理成如下矩阵形式

其中,J为广义质量矩阵,R为广义力矩阵.

2 柔性铰柔性杆机器人的动力学仿真

2.1 验证算例

使用文献[17]中由两个柔性杆和两个柔性铰组成的空间机器人模型,如图2 所示.杆件1 与杆件2 之间的间距为d=0.475 m,由于此间距的存在,杆件1 会发生扭转变形.考虑铰质量产生的项为=5 kg·m2.杆件1 初始角度为π/4,系统在重力作用下运动.取与文献[17]中相同的模型参数,如表1 所示.

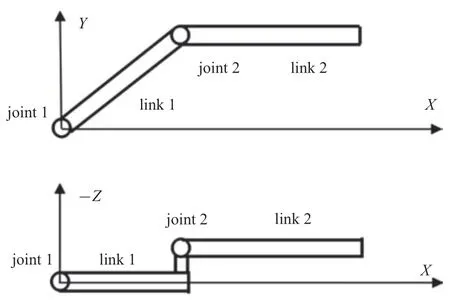
图2 柔性二连杆机器人Fig.2 The flexible robot with two joints and two links

表1 柔性机器人杆件参数Table 1 The parameters of the flexible robot

将本文不考虑铰阻尼时(即双下划线项为零时)杆1 的扭转变形与参考文献[17]中杆1 的扭转变形进行对比,如图3 所示.本文结果与文献[17]中结果一致,验证了本文建模和程序的正确性.

2.2 柔性单铰单杆机器人动力学仿真

图3 结果对比Fig.3 The comparison of results from the present model with those from Ref.[17]

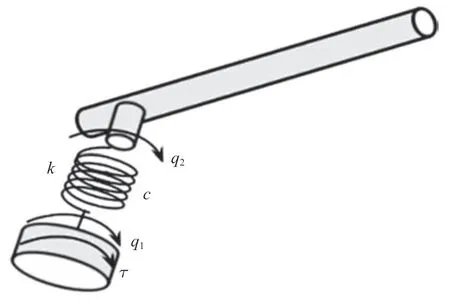
图4 柔性单铰单杆模型Fig.4 The flexible robot with single joint and single link

柔性单铰单杆机器人模型如图4 所示.柔性杆长度L=1.8 m,杆密度ρ=2.766×103kg/m3,杆的横截面积S=2.5×10−4m2,杆截面惯性矩I=1.302 1×10−10m4,杆的弹性模量E=6.9×1010N/m2,驱动转子齿轮的传动比ni=10,驱动转子的转动惯量Jr=7.0×10−3kg·m2.q1为驱动转子传到铰上的角位移,q2为铰传到杆件的角位移.驱动力矩为τ,铰的刚度系数为k,铰的阻尼系数为c.由于铰柔性的存在,铰存在扭转变形,驱动转子上的驱动转角q1并不等于杆件的实际转角q2.

输入的驱动力矩为

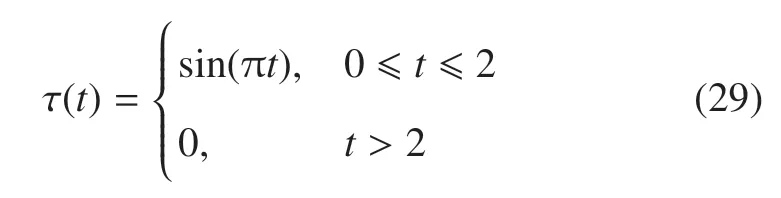
该驱动力矩的大小为一个周期的正弦函数,故对于刚性铰刚性杆机器人,在所给力矩作用下,机器人从静止开始转动,先加速后减速最终回到静止状态.

2.2.1 铰刚度对机器人动力学响应的影响

为了探究铰刚度对柔性机器人动力学响应的影响,对不考虑铰阻尼时不同铰刚度的情况进行仿真分析.图5 为不同铰刚度时铰的驱动转角.图6 为不同铰刚度时铰的实际转角.图7 为不同铰刚度时驱动转角与实际转角的差值.

图5 铰的驱动转角Fig.5 The driving angular displacements of the joint

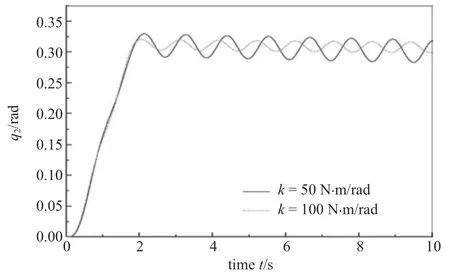
图6 铰的实际转角Fig.6 The actual angular displacements of the joint

图7 驱动转角与实际转角的差Fig.7 The difference between the driving angles and the actuating angles

在刚性铰情况下驱动转角q1和实际转角q2相等,而在柔性铰情况下,铰存在扭转变形,驱动转角q1和实际转角q2不相等.铰的刚度越大,驱动转角q1和实际转角q2越接近.随着铰刚度的增大,驱动转角q1和实际转角q2的振动幅值变小,振动频率变大.故可调节铰的刚度系数的大小来实现柔性机器人的减震和控制.

2.2.2 铰阻尼对机器人动力学响应的影响

为了探究铰阻尼对柔性机器人动力学响应的影响,对相同铰刚度时不同铰阻尼的系统进行仿真分析.将柔性铰的刚度取k=50 N·m/rad.图8 为不同铰阻尼时铰的驱动转角.图9 为不同铰阻尼时铰的实际转角.图10 为不同铰阻尼时铰驱动转角与实际转角的差值.

图8 铰的驱动转角Fig.8 The driving angles of joint

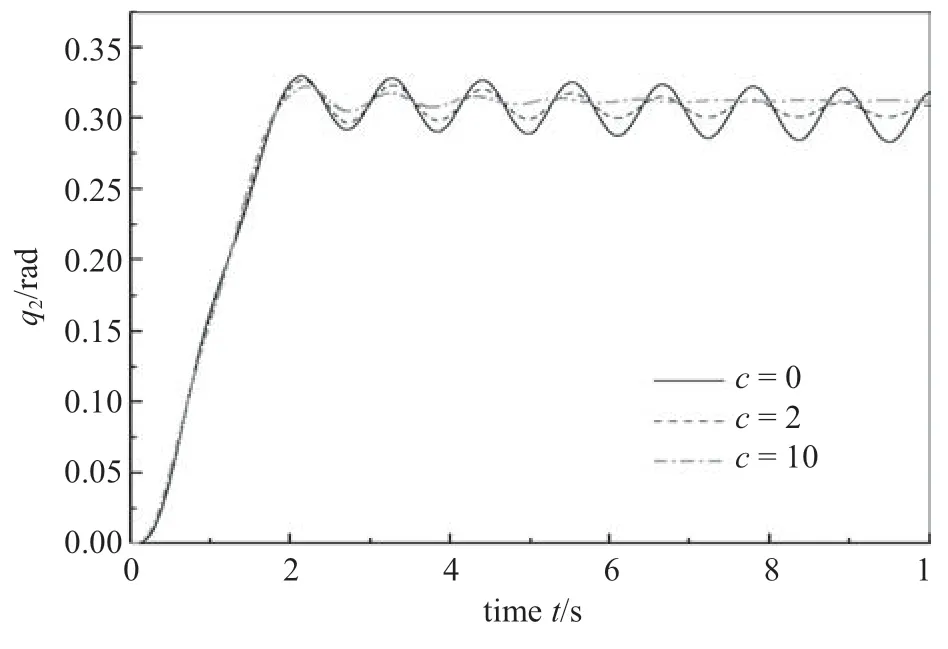
图9 铰的实际转角Fig.9 The actuating angles of joint

图10 驱动转角与实际转角的差Fig.10 The difference between the driving angles and the actuating angles

不考虑铰阻尼时,驱动转角q1、实际转角q2、会一直振动下去.铰阻尼的存在,会使驱动转角q1、实际转角q2的振动衰减.且铰阻尼越大,驱动转角q1、实际转角q2衰减越快.故可调节铰阻尼系数的大小来实现柔性机器人的减振和控制.

3 铰柔性对机器人动力学控制的影响

机器人控制属于动力学逆问题,即已知系统轨迹对应的位移、速度和加速度求解所需关节力或力矩.在系统动力学方程中,广义力可分为与控制有关的广义力和包含了重力、离心力等与控制无关的其他部分的广义力.其中,控制广义力作为控制变量,对机器人运动实施跟踪控制.这里,控制广义力可以是作动器驱动力、阻尼力、弹簧力或者它们的线性组合.为求解此控制变量,首先需要建立系统无控制时的动力学方程,通过在此动力学方程中添加机器人末端运动所需要的约束方程,建立机器人系统带有约束方程的动力学微分代数方程.其次,按照相关控制要求,释放一定数量的控制变量,在此情况下求解微分代数形式的动力学方程,获得满足运动需求的系统运动参数.最后由求解得到的运动参数,通过逆动力学求解得到所需要的控制变量,以此控制变量为前馈输入,再通过反馈控制方法(如PID 方法)施加到系统上,便可使系统完成指定的运动.

以图11 所示机械臂为例,系统由3 根刚性杆和3 个转动铰组成.系统参数为:Li=7.11 m,ρiSi=44.287 kg/m,=5 kg·m2,i=1,2,3.使三连杆末端执行器做如下圆周运动

式中r=5 m,ω=0.314 rad/s,β=−π/2.

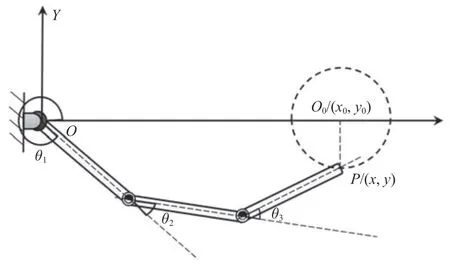
图11 三连杆机械臂Fig.11 Three-link robot

在刚性铰情况下,经过逆动力学求解得到机械臂3 个铰上所需施加的驱动力矩如图12 所示,此刚性铰系统的运动位形如图13 所示.

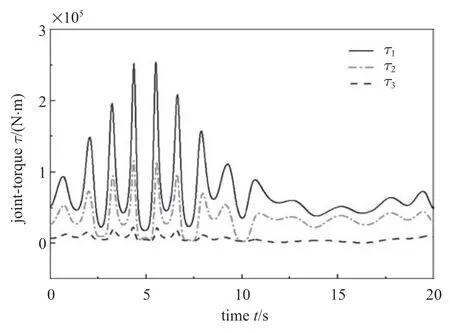
图12 关节力矩Fig.12 The joint-torques

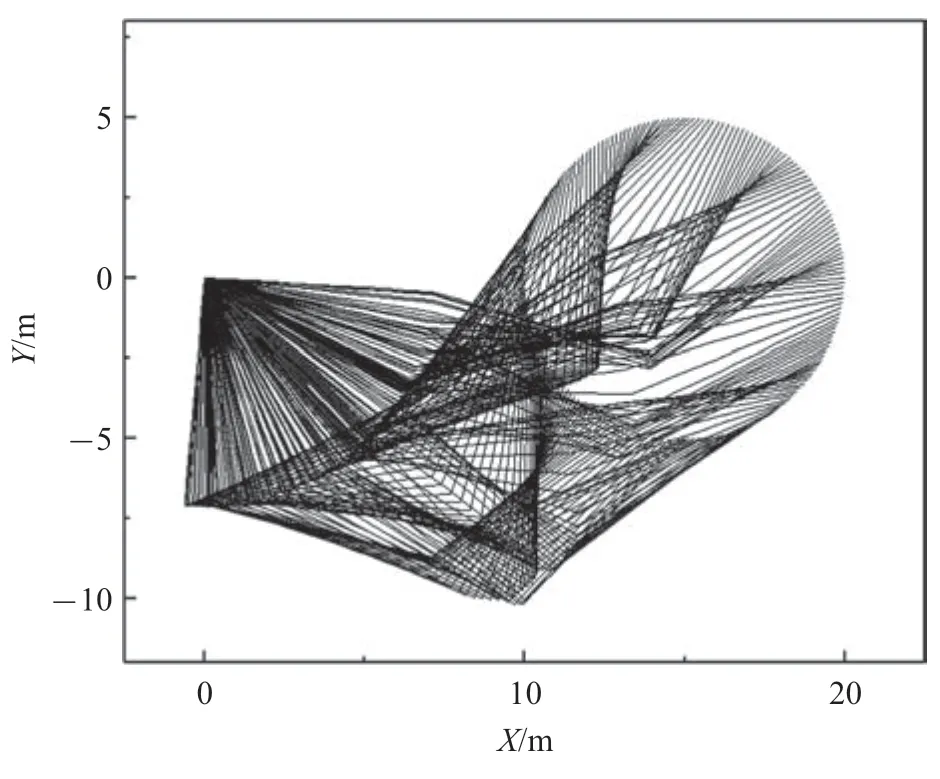
图13 三连杆机械臂的位形Fig.13 The configuration of the 3-link system

将图12 中刚性铰情况下求得的驱动力矩施加到柔性铰系统时,得到柔性铰系统末端执行器的运动轨迹如图14 所示.此时,柔性铰的刚度取k1=k2=k3=1330 N·m/rad.

图14 末端执行器运动轨迹Fig.14 The movement of end-effector

由图14 可见,杆末端轨迹为不规则运动,与指定圆周运动差别巨大.因此在机器人动力学控制时,铰的柔性不可忽略,需要对柔性铰系统进行研究.对柔性铰系统进行动力学逆问题求解得到的3 个铰上所需施加的驱动力矩如图15 所示.

图15 关节力矩Fig.15 The joint-torques

由图12 和图15 可见,完成相同指定运动,柔性铰情况下所需的驱动力矩小于刚性铰情况下所需的驱动力矩.将图15 力矩施加在柔性铰系统上,得到柔性铰的三连杆机械臂运动的位形与图13 一样.

4 结论

本文对考虑铰阻尼的柔性铰柔性杆机器人进行动力学建模,推导出包含杆扭转变形、铰质量效应的刚柔耦合动力学方程.并对两个具体模型进行仿真,得到以下结论:

(1)随着柔性铰刚度的增大,柔性铰柔性杆机器人的动力学响应幅值减小.

(2)铰阻尼的存在,会使系统的振动衰减.随着柔性铰阻尼的增大,柔性铰柔性杆机器人的动力学响应衰减变快.

(3)在机器人动力学控制时,铰的柔性不可忽略.