重复使用火箭着陆结构稳定性分析1)
袁 晗 王小军 张宏剑 石玉红 张 希 章 凌
(北京宇航系统工程研究所,北京 100076)
(中国运载火箭技术研究院,北京 100076)
引言
运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一.因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义.余梦伦[1]指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性.美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2].美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达3~4 亿美元[3].美国的太空探索技术公司(SpaceX)的猎鹰9 号(Falcon-9)火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于2017 年成功实现了回收的火箭一子级的重复使用[4],实现一子级重复使用后,其单次发射费用从6120 万美元降低至4280 万美元[5].猎鹰9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6].
猎鹰9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3].最早的垂直起降验证机为1993 年麦道公司(McDonnell-Douglas)研发的三角快帆(Delta Clipper)验证机[7],对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证.欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8].我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少.夏元明等[9]对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考.聂宏等[10-11]对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响.杨文淼等[12]针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险.毕春莹等[13]设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用Matlab 进行了编程建模和利用Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似.
火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作.目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度.美国关于月球着陆器着陆稳定性的研究集中于20 世纪60 年代至70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14-15],提出四条腿在稳定性与重量上为最优的方案[16].2000 年Doiron 等[17]总结了阿波罗计划时期关于月球着陆器软着陆过程的研究.国内关于月球着陆器着陆稳定性的研究是21 世纪以来伴随“嫦娥”探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18],采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19],并采用动力学试验对仿真分析结果进行验证[20],能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能.聂宏[21-22]采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究.邓宗全等[23-25]采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中.卿启湘等[26]对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为22.5◦时着陆稳定性最为恶劣.
基于能量的方法具有简洁、对精细化的动力学模型依赖较少的优点,但是其结论较为保守,尤其是能量法将触地时所有动能均视为翻倒能,但动力学仿真表明,当着陆腿中含有塑性缓冲吸能材料时,着陆时竖直方向速度的大小对不翻倒对应的参数边界的影响较小[13].基于动力学仿真的方法及实验的方法结论更为准确,但是其分析过程对精细化的动力学模型较为依赖,而在重复使用火箭的方案设计初期确定着陆腿的几何参数时,由于对象尚未确定,往往难以建立精细的动力学模型,所以难以采用动力学仿真或实验的方法.火箭着陆问题为含摩擦的多点碰撞问题,基于广义碰撞定律(generalized impact law)的运动学研究可以在方案设计初期,对着陆稳定性分析提供借鉴.目前基于运动学方法对着陆器着陆稳定性的研究较少,Brogliato 等[27]曾将广义碰撞定律应用于Rocking Block 问题,讨论了黏滞和无摩擦状态下二维Rocking Block 问题中碰撞后速度的取值范围.
Rocking Block 问题首先由Housner[28]在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具等的晃动问题时提出.该问题研究放置于平台上受到平台单边约束的物体(称为浮放物体)在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞.对二维的Rocking Block 问题,碰撞通常采用两点碰撞模型[27-36]或线碰撞模型[37].Shenton 等[29-30]分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31]对长细比为1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维Rocking Block 问题进行了实验研究,观察到了Free Rocking 和Half Rocking 两种运动模式;王琪等[32-35]对含摩擦碰撞中黏滞--滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36]采用一种处理含摩擦多点碰撞问题的方法(LZB 法[38-39])对Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数.张宏剑等[37]将LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性.
本文采用广义碰撞定律,根据单边约束条件和碰撞中的机械能损失,对平面运动着陆模式下火箭与平台碰撞中广义恢复系数的值域进行了探讨.本文首先对火箭和平台建立刚体平面运动模型,将该种着陆模式下空间的四点碰撞问题简化为平面的两点碰撞问题,然后根据动力学方程和单边约束条件,给出了广义恢复系数的值域,然后讨论了黏滞、光滑和滑动摩擦条件下,Free Rocking 和Half Rocking 两种碰撞后运动模式广义运动学恢复系数的值域,对于箭体与着陆平台完全非弹性碰撞的情况,给出了由其几何构型所决定的广义运动学恢复系数,最终提出了一种基于广义碰撞定律的着陆稳定性判别方法,简称GKILSC 法(generalized impact law based stable criterion method).
1 系统动力学模型
对于重复使用运载火箭的着陆过程,依据四条着陆腿是否存在同时落地,可以分为4,2-2,1-2-1,1-1-1-1 共4 种着陆模式,其中4 模式表示4 条着陆腿同时落地;2-2 模式表示先有两条腿同时落地,再有两条腿同时落地;1-2-1 模式表示先有1 条腿落地,然后两条腿同时着地,最后再有1 条腿落地,这里考虑了着陆腿的形变导致着陆过程中4 条腿的着陆点不恒共面;1-1-1-1 模式表示4 条腿不同时依次落地;其中2-2 模式和1-2-1 模式均为平面运动着陆模式,有研究通过三维动力学仿真表明,2-2 模式较1-2-1 模式的稳定性更差[25].本文将针对2-2 模式,基于刚体动力学研究其着陆的稳定性.
如图1 所示,在2-2 着陆模式下,形如太空探索技术公司的猎鹰9 号火箭的倒三角式着陆腿(a)和型如蓝色起源太空公司的新谢泼德火箭的平行四边形式着陆腿(b)均可简化为图1 中部所示的平面动力学模型,在采用刚体动力学分析时,两种模型可进一步简化为(c)所示的刚体平面运动的通用等效模型.其质心C距离着陆腿底部的轴向距离为h,着陆腿跨距为2b,质量为m,绕过质心且垂直于运动平面的轴的转动惯量为Jc.

图1 2-2 着陆模式的通用等效模型Fig.1 Universal equivalent model of 2-2 landing mode
1.1 着陆过程动力学模型
箭体与着陆平台的动力学模型如图2 所示,其质心水平坐标为xc,质心距着陆平台高度为yc,箭体倾角为θ,取描述系统的广义坐标q=,1 点、2 点与着陆平台的距离分别为δ1(q),δ2(q).

图2 运载火箭着陆的动力学模型Fig.2 Dynamics model of RLV landing
则箭体受到单边约束

箭体可能在1 点和2 点受到约束面的作用力,设1 和2 两点处的支撑力为Fn,1和Fn,2,摩擦力为Ff,1和Ff,2,则系统的动力学方程为

同时约束面作用力Fn,1和Fn,2与δ1和δ2满足线性互补条件[32-35]

1.2 切向力模型
诸多研究人员对碰撞中的摩擦现象提出了多种摩擦模型,例如库伦摩擦模型、库伦摩擦+黏性摩擦模型、Stribeck 摩擦模型等[40],本文采用经典库伦干摩擦模型,其摩擦力Ff,i为
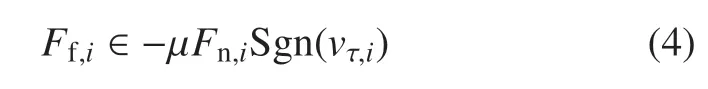
其中,Fn,i为该点支撑力;µ为摩擦系数;vτ,i为碰撞两点切向的相对速度;Sgn(·)为集值函数[35].
对于碰撞过程中的切向冲量Iτ,i=,在这里对碰撞过程中引入假设.
假设1:若碰撞结束后vτ,i(t+)≠0,则在碰撞过程中vτ,i不连续为0,且碰撞过程中始终有

得切向冲量与法向冲量满足

在碰撞过程中切向可能存在黏滞--滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞--滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32-35,38-39,41-42].但在库伦干摩擦模型下恒有≤µIn,i,且在碰撞过程中vτ,i方向不切换的情况下,该不等式取等号.
2 基于广义碰撞定律的分析
2.1 广义碰撞定律
对于受到l个单边约束的n维Lagrange 系统,该系统的广义坐标为q,每个单边约束为φi(q)≥0,1 ≤i≤l,同时系统具有对称正定的广义质量矩阵M(q).同时在该空间下对任意向量ν1,ν2定义内积,则可定义每个单边约束的单位法向量

若这l个单边约束互相独立,则在该Lagrange 系统中共有l个约束面的法向量,且线性无关.同时可找到n−l个单位向量tj,满足正交性=0 和单位性=δij.则可构造一组该Lagrange 系统的基向量{n1,n2,···,nl,t1,t2,···,tn−l},对于该系统中的任意状态p,可由该组基表出p=c1n1+c2n2+··· +clnl+d1t1+d2t2+··· +dn−ltn−l,其中c1,c2,···,cl≥0,即该Lagrange 系统为n维空间的一个广义锥面.定义原坐标到的坐标变换矩阵=(n1,n2,···,nl,t1,t2,···,tn−l)T,进一步定义广义法向速度、广义切向速度

当约束面无摩擦时约束面无法提供切向力,设第i个单边约束的法向约束力为Fn,i,其虚功为δWi=Fn,iδφi(q),进一步得系统受到的约束力的虚功δW=和广义力.其中为一个n×l维的矩阵,此外系统受到广义常规力,如重力等.则广义坐标下系统的动力学方程为.在t时刻系统发生碰撞,表示碰撞开始时刻,t+表示碰撞结束时刻,则碰撞过程中有

在碰撞过程中,引入以下两个假设[38-39]:
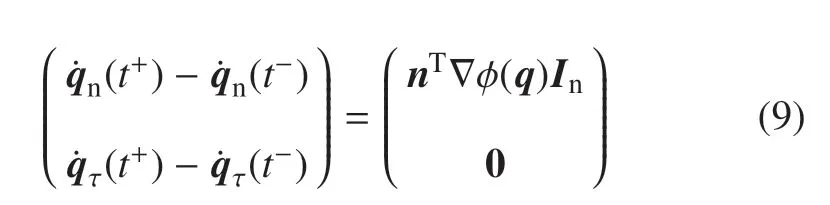
其中n=(n1,n2,···,nl)T,即n为的前l行.
对于含摩擦的碰撞,可定义一个切向恢复系数矩阵ετ,其元素eτ,ii=,即为碰撞前后速度之比.则其广义碰撞定律为

系统无摩擦时其切向恢复系ετ=−In−l,这里In−l表示n−l维单位矩阵.
2.2 一般情况碰撞后速度分析
对于上述运载火箭着陆问题,由式(2)得
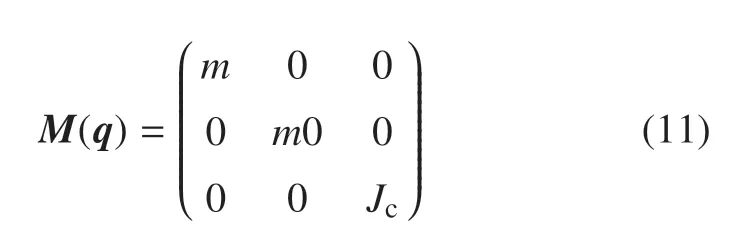
约束方程为式(1),即φ1(q)=δ1(q)≥0,φ2(q)=δ2(q)≥0,由式(6)得正交化的单位向量
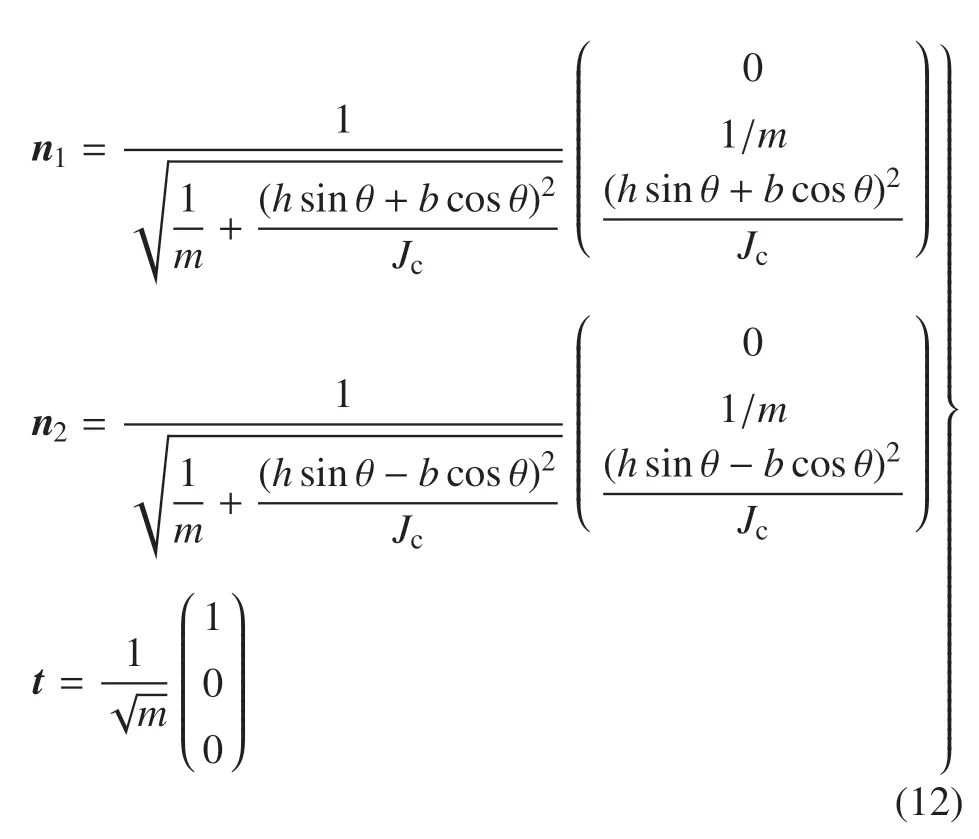
由式(7)、式(11)和 式(12)得
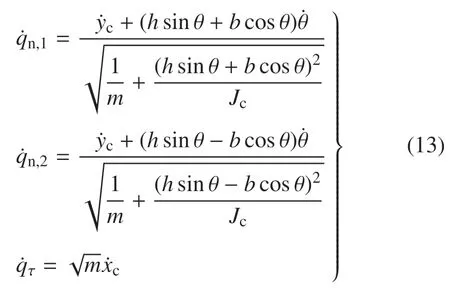
由式(10)得

在运动平面内,考察2 点与地面碰撞后保持与地面接触qn,2=0,=0,1 点悬空且<0,如图3 左侧所示.
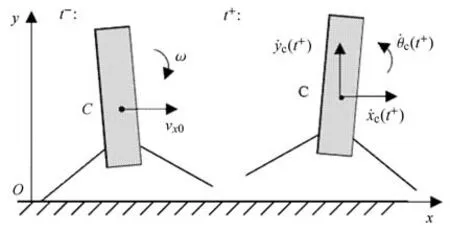
图3 箭体与平台的两点碰撞过程Fig.3 Impact procedure between rocket and platform
在t时刻1 点与地面发生碰撞,即qn,1(t)=0,θ(t)=0,则在t时刻箭体与地面发生多点碰撞,在空间中为四条着陆腿与地面的四点碰撞,在简化的平面运动模型中为两点碰撞,碰撞后运动如图3 右侧所示.碰撞前的速度为
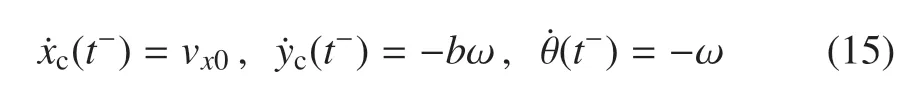
由式(13)得碰撞前的广义速度
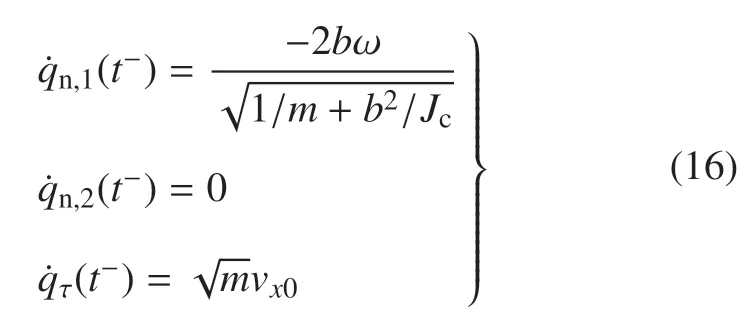
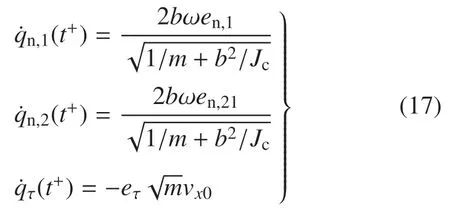
由式(13)和式(17)得碰撞后箭体的速度
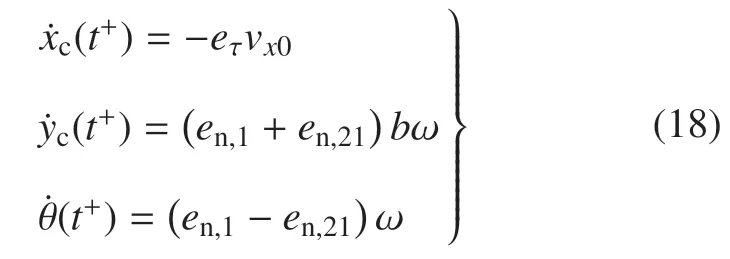
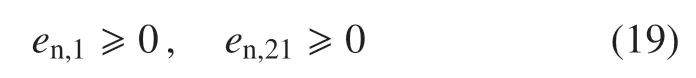
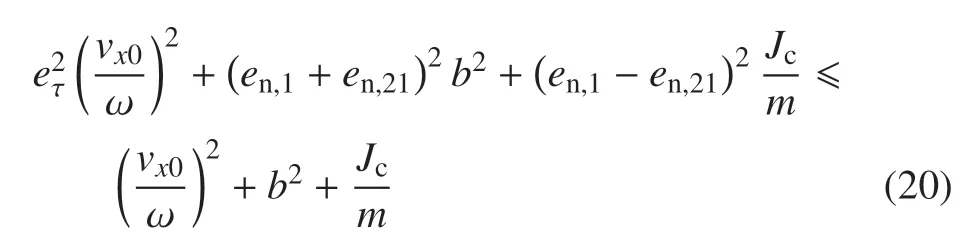
根据动量定理和相对质心的动量矩定理得
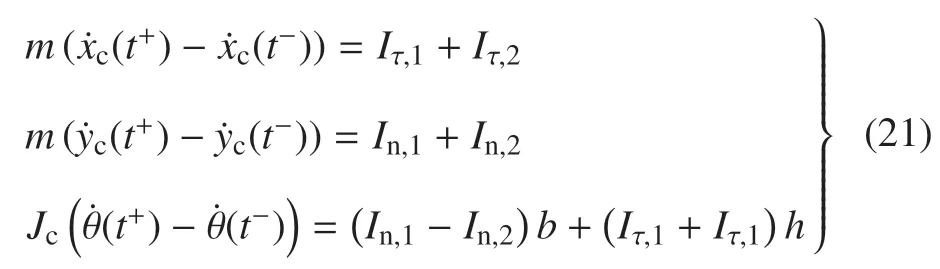
由于在碰撞中Iτ,1与Iτ,2方向相同、作用在同一条直线上,且vτ,1=vτ,2,故Iτ,1与Iτ,2对箭体的影响为耦合的,令Iτ=Iτ,1+Iτ,2,由式(15)、式(18)、式(21),得到3 个冲量
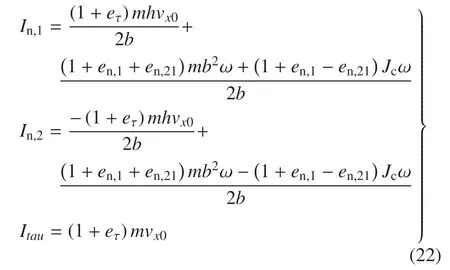
单边约束要求In,1≥0,In,2≥0,得不等式
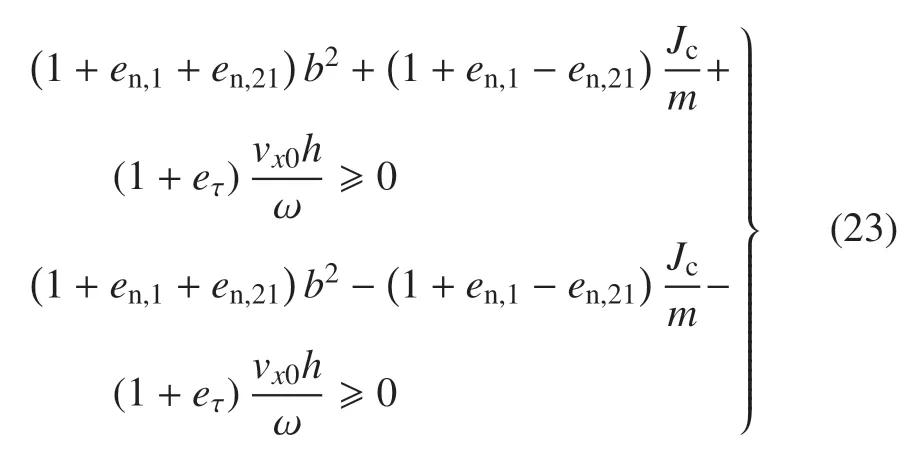
摩擦冲量如式(5)所示,由于碰撞时刻θ(t)=0,令vτ(t)=vτ,1(t)=vτ,2(t),有
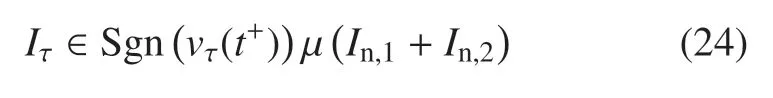
由式(15)、式(18)得碰撞前后接触点的切向速度
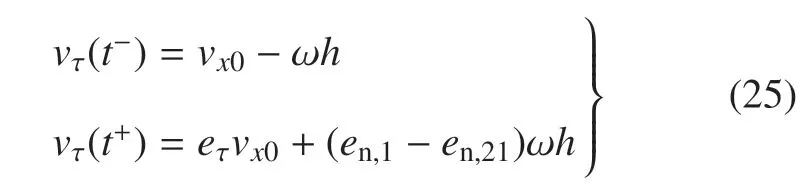
若碰撞过程为滑动摩擦,即vτ(t+)≠0,切向恢复系数
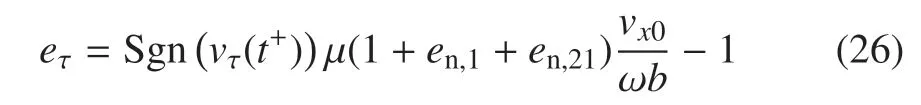
同时vτ(t+)≠ 0 对µ 的上限有约束,按照vτ(t+)>0 和vτ(t+)<0 两种情况进行讨论.
当vτ(t+)>0,由式(25)、式(21)、式(24)得碰撞后接触点的切向速度vτ(t+)=vx0−µ(1+en,1+en,21)ωb+(en,1−en,21)ωh>0,即要求µ满足

当vτ(t+)<0,同理可得vτ(t+)=vx0+µ(1+en,1+en,21)ωb+(en,1−en,21)ωh<0,即要求µ满足

若为静摩擦,碰撞后箭体与地面相对滑移速度为0,则有vτ(t+)=0,由式(25)得几何约束
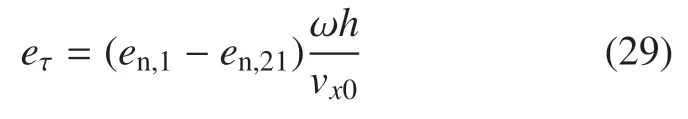
又由于vτ(t+)=0,则Sgn(vτ(t+))2 [−1,1].将式(24)、式(29)代入式(22),得恢复系数en,1,en,21与µ间需满足的关系

总结,广义运动学恢复系数需满足如下条件:
(1)碰撞过程中的机械能损失条件式(20);
(2)运动的单边约束条件式(19);
(3)法向冲量的单边约束条件式(23);
(4)摩擦条件,对于滑动摩擦,其切向恢复系数满足式(26),同时µ需满足要求式(27)、式(28);对于静摩擦,需满足式(29)和式(30).
3 典型运动模式分析
上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27-31,35].若碰撞后1 点与平台保持接触,即en,1=0,en,21≥0,该运动模式称为Free Rocking;若碰撞后2 点与平台保持接触,即en,1≥ 0,en,21=0,该运动模式称为Half Rocking.两种运动模式如图4 所示.下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰撞后黏滞、碰撞前后保持滑动摩擦4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件.
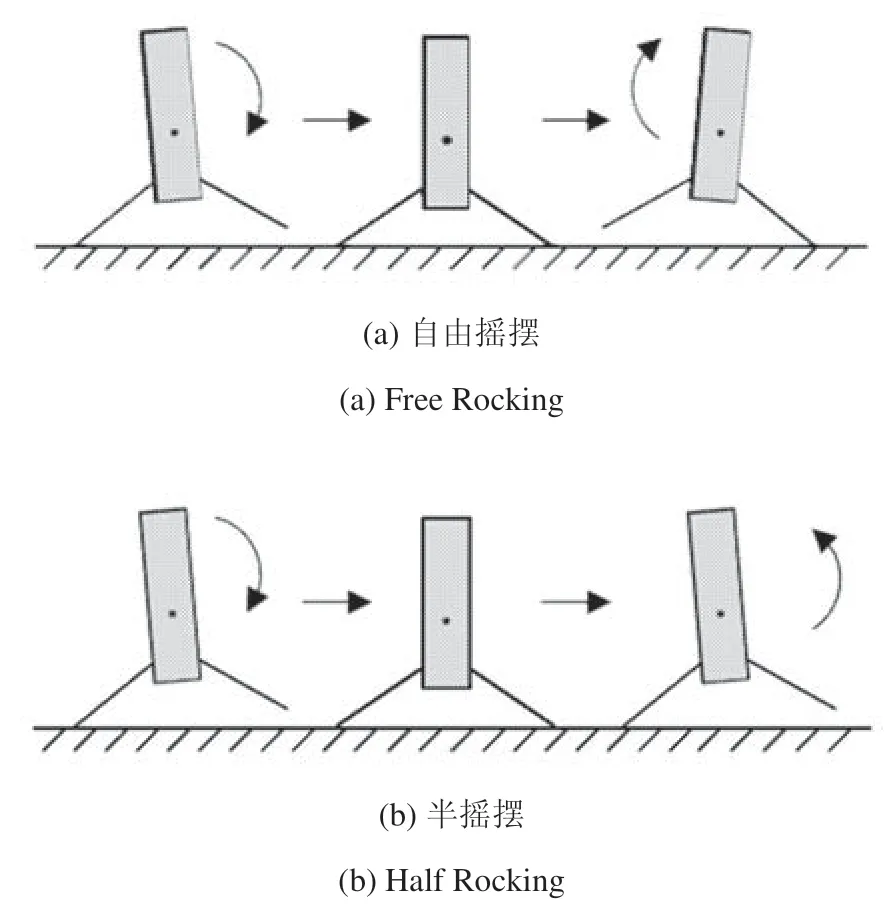
图4 两种典型运动模式Fig.4 The two typical motion
3.1 Free Rocking 模式,碰撞前后保持黏滞
由于碰撞前后均为黏滞状态vτ(t−)=vτ(t+)=0,摩擦为静摩擦,由式(25)得eτ=−en,21.
由式(19)碰撞后单边运动约束和式(20)机械能约束、式(23)冲量的单边约束条件、式(30)静摩擦条件得

3.2 Free Rocking 模式,无摩擦
无摩擦时认为保持滑动且µ=0,Iτ=0,由式(19)和式(20)、式(23)、式(26)得
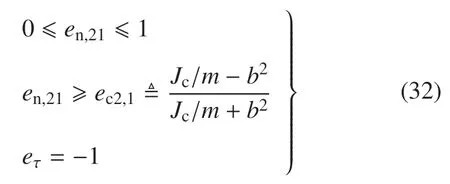
综上所述有en,212[max(0,ec2,1),1].若ec2,1>0,即b2 由于碰撞后为黏滞状态,故摩擦为静摩擦,且有vτ(t+)=0,由式(25)、式(19)和式(20)、式(23)、式(30)得 对于滑动摩擦,需要考虑vτ(t+)正负两种情况. 当vτ(t+)>0,由式(19)和式(20)、式(23)及vτ(t+)>0 的条件式(26)、式(27)得 需证明ec4,1≤ec4,2且ec4,2≥ 0 恒成立.由式(34)可知vx0>en,21ωh+µ(1+en,21)ωb,进一步得 即恒有ec4,1 由式(34)可知µc4,1≤vx0/ωb≤µc4,2.故≤µc4,1均有µc4,1<µc4,2. 当vτ(t+)<0,同理可得 同时,可证恒有ec4,3 由于碰撞前后均为黏滞状态,故摩擦为静摩擦,且有vτ(t−)=vτ(t+)=0,由式(19)和式(20)、式(23)、式(25)、式(30)得 由式(36)的第2 式可知,Half Rocking 模式仅跨距较大时可能发生. 无摩擦时认为保持滑动且µ=0,Iτ=0,由式(19)和式(20)、式(23)、式(26)得 与3.5 结论相似,由式(37)的第2 式可知,Half Rocking 模式仅在跨距较大时才可能发生. 由于碰撞后为黏滞状态vτ(t+)=0,故摩擦为静摩擦,由式(19)和式(20)、式(23)、式(25)、式(30)得 与3.5 节碰撞中保持黏滞相比,若碰撞前向左侧滑动vx0−ωh<0,Half Rocking 运动模式对跨距的要求更低;若碰撞前向右侧滑动vx0−ωh>0,Half Rocking 运动模式对跨距的要求更高. 对于滑动摩擦,需要考虑vτ(t+)正负两种情况. 当vτ(t+)>0,由式(19)和式(20)、式(23)、式(26)、式(27)得 需证明ec8,1≥0 恒成立.由µ<µc8,1得vx0/ωh>(1+en,1)µb/h−en,1,进一步得 由en,1≥0 可证不等式右侧≥0,则ec8,1≥0.故有. 当vτ(t+)<0,同理可得 同时可证恒有ec8,2≥0,此. 由上述分析可知,在Half Rocking 运动中单边约束式(23)将简化为几何约束,且该种运动模式仅在跨距较大时才可能发生. 表1 2 种典型运动模式运动学恢复系数的值域和必要条件Table 1 The kinematic restitution coefficient and necessary condition of 2 typical behavior 表1 2 种典型运动模式运动学恢复系数的值域和必要条件(续)Table 1 The kinematic restitution coefficient and necessary condition of 2 typical behavior(continued) 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9,12,18-23,26]、油液缓冲器[11,13]或混合缓冲器[10],使得箭体与地面的碰撞接近完全非弹性碰撞.对于完全非弹性碰撞,碰撞后的运动模式为Free Rocking 或在纵向静止[27],即碰撞后其en,1=0,en,21为3.1~3.4en,21中的下界.下面将从3.1~3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. 当µ较大、碰撞时水平速度vx0绝对值较小,碰撞后可出现黏滞状态,即vτ(t+)=0.当vx0沿负向增大,则会出现vτ(t+)<0 的运动状态,即在图2 所示的坐标系下,接触点向左滑动;反之当vx0沿正向增大,则vτ(t+)>0 接触点向右滑动,接下来分别讨论3 种运动状态及其临界情况. 对碰撞后接触点向左滑动和黏滞的临界情况,µ与速度需满足式(41),定义此时的临界速度比(vx0/ωh)ch1如式(42),其中ec4,3由式(35)给出 若vx0/ωh<(vx0/ωh)ch1,运动状态为碰撞后接触点向左滑动,en,21=ec4,3,eτ由式(35)给出.对碰撞后接触点黏滞与向右滑动的临界情况,µ与速度需满足式(43),临界速度比(vx0/ωh)ch2如式(44) 若vx0/ωh>(vx0/ωh)ch2,运动状态为碰撞后接触点向右滑动,en,21=ec4,1,eτ由式(34)给出. 若(vx0/ωh)ch1≤vx0/ωh≤ (vx0/ωh)ch2,运动状态为碰撞后黏滞,en,21=ec3,1,eτ由式(33)给出.由ec3,1,ec4,1,ec4,3的表达式可知ec4,3≤ec3,1≤ec4,1,即ec4,3和ec4,1分别为en,21的下界和上界. 3.1 中所分析的箭体与平台碰撞前后接触点均保持黏滞所示的运动状态,为当(vx0/ωh)ch2≥1 时,3.3 所分析的碰撞后黏滞的运动状态在vx0/ωh=1 时的特殊情况;3.2 所分析的无摩擦的运动状态,为当µ=0 时,3.4 滑动摩擦的特殊情况. 根据上述分析,考虑单边运动约束en,21≥0,en,21与碰撞前速度比vx0/ωh的关系可总结如表2. 表2 完全非弹性碰撞中运动学恢复系数Table 2 Kinematic restitution coefficient in completely inelastic collision 由式(34)可知,当µh≥b时ec4,1>1,即在向右滑动时碰撞后角速度增大,即虽然碰撞后总机械能降低,但是在摩擦的作用下,使得箭体的角速度增大,进而增大了箭体翻倒的可能,该种情况仅可能发生在摩擦冲量向左时.由式(35)可知恒有ec4,3<1,即当运动状态为箭体与平台碰撞后向左滑动时,碰撞后箭体的角速度必然降低. 本文虽然没有对碰撞过程中接触点黏滞--滑移的状态切换过程进行判断,但在经典库伦干摩擦模型描述摩擦力的前提下≤µIn,i恒成立,由上述分析可知,结论ec4,3≤en,21≤ec4,1及ec4,3,ec4,1的取值与碰撞过程中对黏滞-滑移状态的判断方法无关,仅影响(vx0/ωh)ch2和ec3,1的取值.若对上述切换过程进行动态判断,当0 可见vx0/ω 较小,甚至为负,更有利于着陆稳定,由于,故在图3 所示的坐标系下同号更有利于着陆稳定. 表3 碰撞后停止的必要条件Table 3 Necessary condition of motionless after impact 本节讨论当1 点接触平台且˙θ<0 时,箭体是否向右侧翻倒的问题.在碰撞结束到翻倒过程中,1 点与地面保持接触,接触状态可能为黏滞、保持滑动、先滑动后黏滞,同时滑动需考虑两个方向.本节基于能量法提出一种考虑摩擦的不翻倒的判断方法.首先,不翻倒的充分条件为其的动能小于翻倒所需的重力势能,如式(45).这里为讨论方便,动能和和重力势能均除以质量 为便于分析,设一直线平移坐标系P系(非惯性系),其y轴固连于质心,x轴与大地坐标系重合,如图5 所示.在该系中质心水平速度=0,箭体受过质心的重力、惯性力FI,过1 点的支撑力Fn,1、摩擦力Ff,1,翻倒过程中仅重力和Ff,1做功. 图5 直线平移坐标系Fig.5 Straight-line translation coordinate 若不考虑摩擦,Ff,1=0,不翻倒的条件为 定义摩擦角ϕµ=arctan(µ).当>0 且翻倒过程中1 点相对着陆平台始终向右滑动,Ff,1<0,在P系中摩擦力做正功,且若箭体质心与1 点连线与竖直方向夹角αc1<ϕµ便会翻倒.当αc1>ϕµ箭体质心加速度具有向下的分量,则Fn,1≤mg,故翻倒过程中≤µmg.在P系中考察箭体从θ=0 转动到跨过摩擦角的过程,若初始动能和摩擦力做功小于重力势能变化,则不会翻倒,不翻倒的条件为 式(45)~式(47)为不翻倒的充分条件,定义翻倒能量Efall和无量纲的稳定系数γstable,不翻倒需满足式(48),静止时γstable=1. 第三章的分析均为分析火箭以2-2 模式着陆时箭体与着陆平台的第二次碰撞,在本节中将考虑在2-2 着陆模式下箭体与着陆平台的第一次和第二次碰撞,以碰撞后不翻倒为稳定条件给出一种小姿态角下着陆稳定性判别方法,碰撞均视为完全非弹性碰撞,其碰撞过程如图6 所示,坐标系与图2 一致,其中表示第j次碰撞中i点的法向冲量. 图6 箭体着陆碰撞过程Fig.6 Landing impact procedure of the rocket 首先假定第一次碰撞保持黏滞,碰撞时的切向冲量与法向冲量为 在前期设计时,在小姿态角着陆情况下难以判断第一次碰撞发生在1 点还是2 点,故应考虑两种情况并取不利的情况作为着陆速度的限制. 该法为即为GKILSC 法. 以文献[10]中采用的四腿式火箭垂直着陆原理样机为例,考察完全非弹性碰撞下火箭的着陆过程.该样机在2-2 着陆模式下b=3.43 m,着陆腿展开后质心高度h=7.27 m,着陆体总质量m=5400 kg,其中着陆腿重200 kg,µ=0.3,绕质心转动惯量Jc=1.354×105kg·m2.由式(42)、式(44)得 对于上述参数,由表2 得en,21与vx0/ωh的关系如图7 所示.对其跨距进行调整,分析跨距对恢复系数ec4,3,ec4,1及其对应的临界速度比(vx0/ωh)ch1,(vx0/ωh)ch2影响,半跨距b取2~6 m,由于着陆腿质量仅为200 kg,故可近似忽略跨距变化对转动惯量的影响,结果如图8 所示.对µ进行调整,分析µ对恢复系数ec4,1,ec4,3及其对应的临界速度比影响,同样保持其他参数与文献[10]一致,µ取0 到0.8,结果如图9 所示. 图7 恢复系数与速度比Fig.7 Restitution coefficient and speed ratio 由图8(a)可见ec4,1,ec4,3均随跨距增大而减小,即随跨距增大着陆过程更稳定.由于,故当ec4,3≤ 0 时表示当vx0/ωh小于某个临界速度比时en,21=0,即箭体停止摇晃.当ec4,1≤ 0 时表示无论何种速度比碰撞后均停止摇晃.由图8(b)可见两个临界速度比均随跨距增大而减小,说明随跨距增大,发生碰撞后向右滑动对速度比的要求降低,发生碰撞后向左滑动对速度比要求升高.同时,在同样的vx0/ωh下,en,21随着b的增大而减小,直到en,21=0. 图8 着陆腿跨距的影响Fig.8 Result of leg span 由图9(a)可见,µ=0 时ec4,1=ec4,3=0.361 3,即ec2,1.随着µ增大,ec4,3和(vx0/ωh)ch1减小,ec4,1和(vx0/ωh)ch2增大,即摩擦力对转动角速度的影响增大,在摩擦较大的情况下应尽量使得着陆前与同号.由图9(b)可见随着µ增大,发生碰撞后黏滞的可能性增大. 采用上述稳定性判别方法对上述模型计算其着陆的速度容许范围,即γstable=0 对应的着陆速度.不同下落速度的速度容许范围见图9(a);取不同跨距,=−3 m/s,其他参数不变,速度容许范围见图9(b);取不同的摩擦系数,=−3 m/s,其他参数不变,速度容许范围见图9(c). 图9 摩擦系数的影响Fig.9 Result of friction coefficient 在小姿态角着陆时需要考虑第一次碰撞发生在1 点或2 点两种情况并分别计算其γstable并对二者取不利情况,即取两种情况γstable的较小值.则对任意着陆速度在着陆稳定分析中其γstable与对应的γstable相等,可见图9 所示的稳定速度边界也具有这种对称性.由图9(a)可见,在图2 所建立的坐标系下着陆前角速度与切向速度同号时着陆更稳定,竖直下降速度对稳定性的影响较为复杂,但稳定区间差别较小,与动力学仿真的结论相似[12].同时=−5 m/s 与−1 m/s 和−3 m/s 两种速度在角速度与切向速度同号且较大时速度容许范围边界的趋势不同,是由于其翻倒模式不同.以>0 为例,=−5 m/s 时其翻倒模式为首先在1 点发生碰撞后再发生第二次碰撞,随后绕2 点翻倒;而=−1 m/s 或−3 m/s 时其翻倒模式为在2 点发生碰撞后绕2 点翻倒,不发生第二次碰撞.对于图9(b)b=2 m 时,且较大时翻倒模式与图9(a)=−5 m/s 时相同,同时由图9(b)可见随着陆腿跨距增大稳定性增强.由图9(c)可见随着µ增大在较大、较小时着陆更稳定,在较小、较大时着陆更不稳定,考虑到垂直着陆时水平速度通常较小,故µ增大有利于着陆稳定.若干算例对应的容许速度范围的边界沿水平轴无限延伸,此时为判据式(47)所示的情况,即始终保持滑动也不会翻倒. 图10 参数对速度容许范围的影响Fig.10 Admissible speed domain in different parameters 图10 参数对速度容许范围的影响(续)Fig.10 Admissible speed domain in different parameters(continued) 图11 能量法与本文方法速度容许范围的对比Fig.11 Admissible domain of speed comparison between Energy method and GKILSC method 本文基于广义碰撞定律,对重复使用运载火箭在2-2 着陆模式下的着陆稳定性问题进行了研究,本文首先将该种着陆模式下火箭与平台的碰撞简化为平面运动两点碰撞问题,采用单边约束条件刻画竖直方向上的速度和冲量,采用经典库伦干摩擦模型刻画切向冲量.同时考虑机械能的约束,给出了该着陆模式下火箭与平台发生多点碰撞后速度的值域. 对于浮放物体实验中观测到的Free Rocking 和Half Rocking 碰撞后两种运动模式,分别考虑了滑动摩擦和静摩擦状态下,给出了碰撞过程中恢复系数的值域.最后基于实际工程中碰撞为接近完全非弹性碰撞的情况,给出了碰撞后切向速度和角速度与碰撞前切向速度和角速度的表达式,并提出了一种着陆稳定性的判别方法,该法形式较为简单,通过近似和简化避免了积分过程,适用于前期着陆稳定性估计.随后通过算例分析了着陆腿跨距、摩擦系数对第二次碰撞中的广义运动学恢复系数和着陆稳定的速度容许范围的影响,以及不同竖直速度、着陆腿跨距、摩擦系数在水平速度--角速度剖面上对应的稳定要求的速度容许范围. 结论表明:稳定性随着着陆腿跨距增大而提高,摩擦系数越大稳定性受水平速度的影响越大,在水平速度的较小时稳定性随着摩擦系数增大而提高,竖直速度对稳定性的影响较小.在图2 所建立的坐标系下,角速度与切向速度同号时,着陆稳定性更好;当角速度与切向速度异号时,第二次碰撞过程中存在摩擦冲量使得箭体转动速度增大的风险,使得稳定性降低. 本文对碰撞过程中摩擦的分析为基于冲量的,没有对接触碰撞过程中接触点的黏滞--滑移的状态切换过程进行判断.但由于着陆过程中的最不利工况出现在碰撞后向左或向右滑动,且由4.1 的分析可知本文的假设更为保守,故本文的研究工作适用于实际工程的运载火箭着陆稳定性分析,可用于指导工程设计.3.3 Free Rocking 模式,碰撞前滑动、碰撞后黏滞

3.4 Free Rocking 模式,碰撞前后保持滑动摩擦
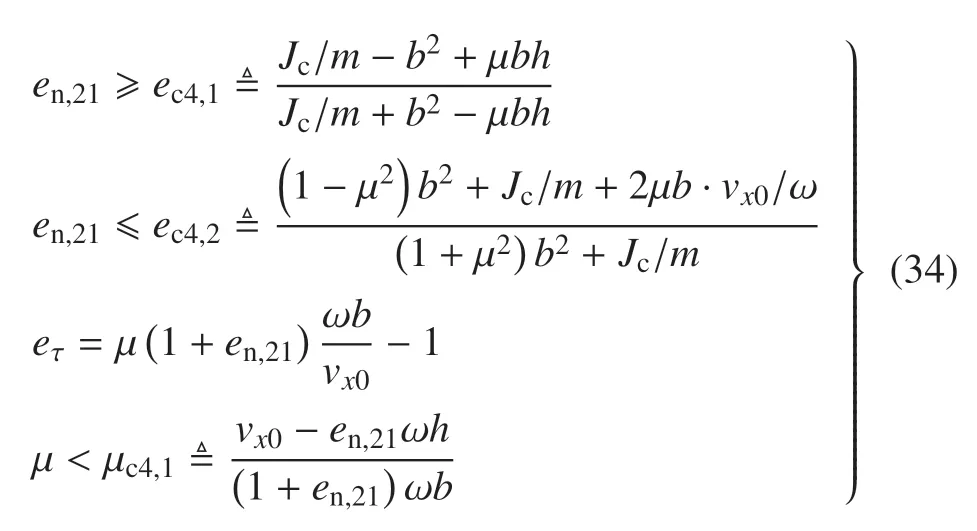
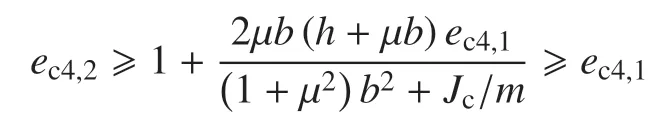


3.5 Half Rocking 模式,碰撞前后保持黏滞

3.6 Half Rocking 模式,无摩擦状态

3.7 Half Rocking 模式,碰撞前滑动、碰撞后黏滞
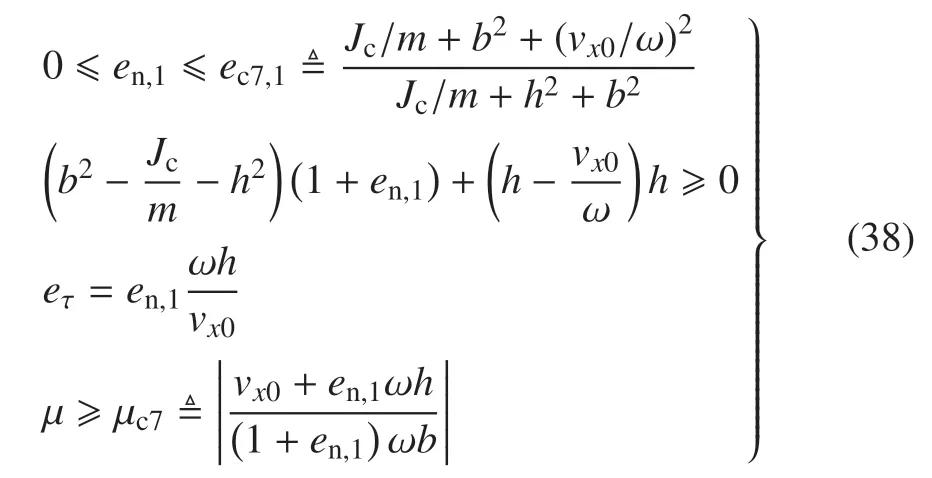
3.8 Half Rocking 模式,碰撞前后保持滑动摩擦

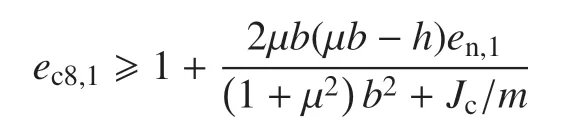
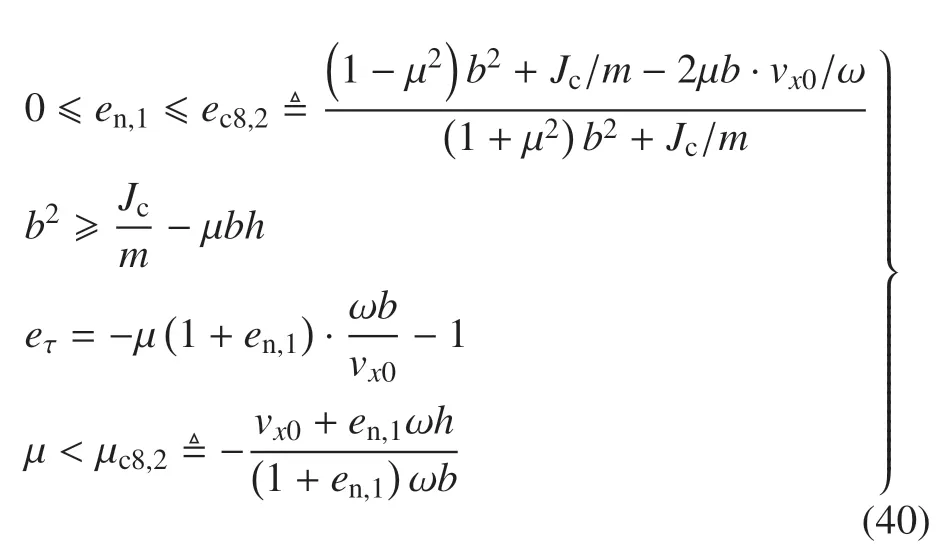


4 基于完全非弹性碰撞假设的箭体着陆
4.1 不同速度组合下的运动学恢复系数

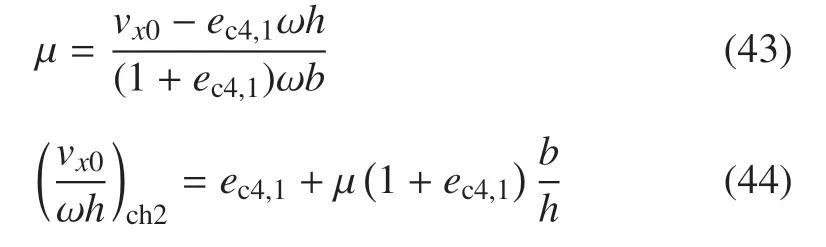
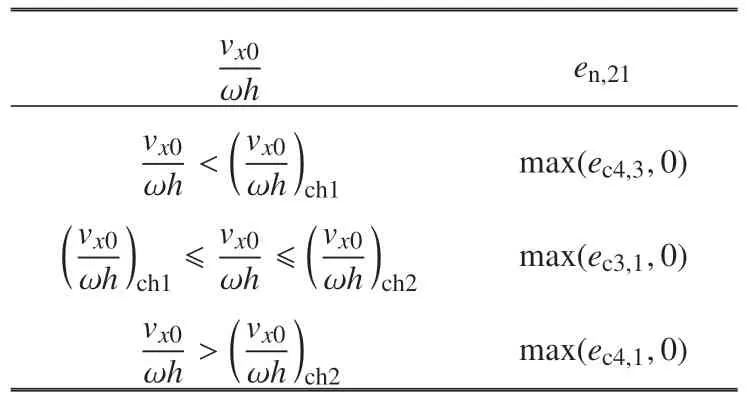

4.2 翻倒评价准则
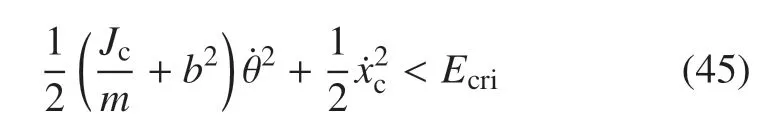
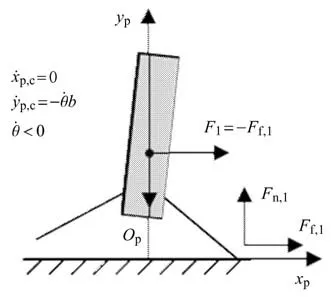

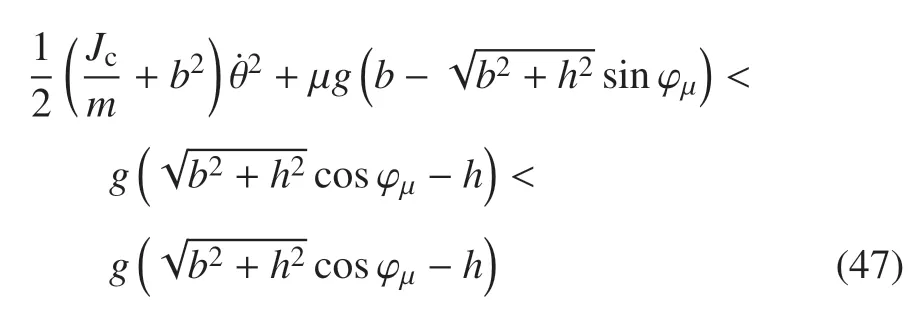
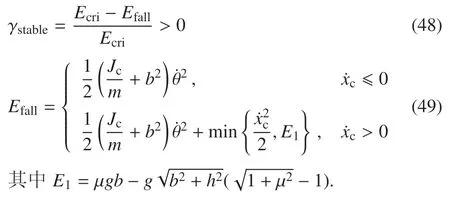
4.3 静止平台着陆稳定性判别方法
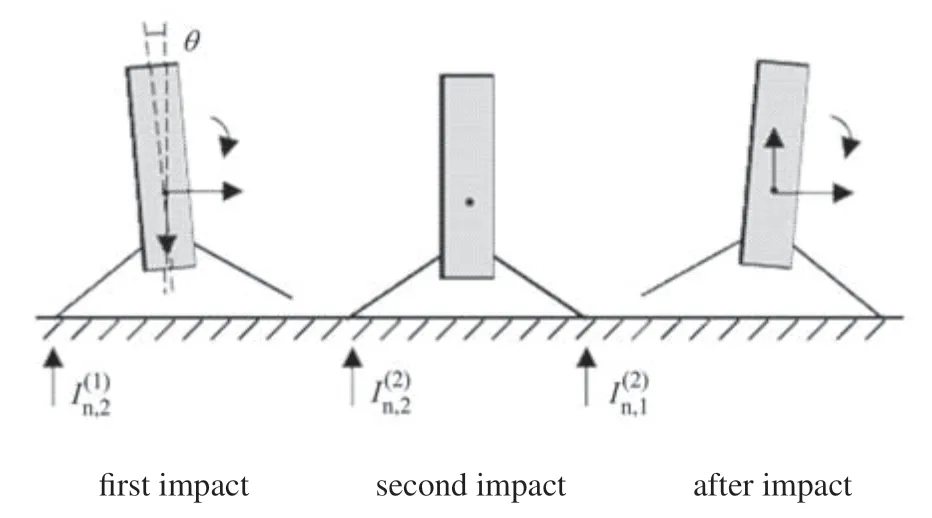
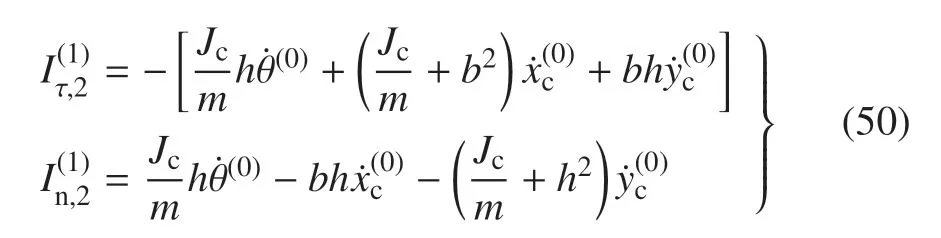

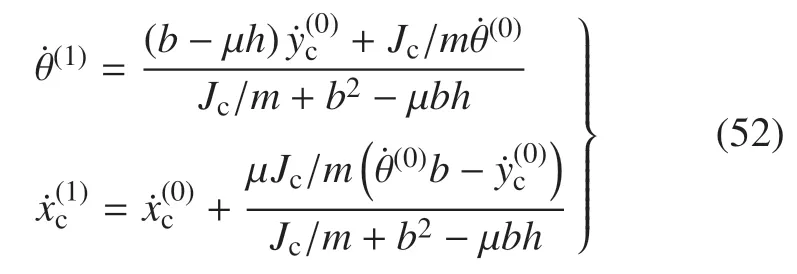

5 算例



6 结论

