机械臂臂杆刚度主动控制下的末端振动特性研究1)
张玉玲 谷勇霞 赵杰亮 阎绍泽
(清华大学摩擦学国家重点实验室,北京 100084)
(北京工商大学材料与机械工程学院,北京 100048)
引言
随着航天技术的发展,空间机械臂成为辅助甚至代替人类从事各种太空作业的重要在轨服务工具[1].空间机械臂具有质量轻、工作半径大、高负载能力等特征,在运动过程中会因臂杆柔性引发结构变形和弹性振动,降低机械臂末端的定位精度和运动稳定性,成为机械臂研究中的突出问题[2-3].
早期国内外学者为了解决柔性机械臂的弹性振动问题对机械臂的动力学建模、控制策略及实验方面进行了大量的研究,理论模型不断得到完善,控制策略也趋于智能化,极大地提高了机械臂动力学特性的分析精度.目前主要结合模态分析法等离散化方法等[4]和经典建模方法建立理论模型,然后采用PD 控制、鲁棒控制、奇异摄动等经典控制方法及神经网络控制、模糊控制等智能控制方法抑制振动及轨迹跟踪[5-12].Yang 等[13]结合假设模态法和Lagrange 方程建立了空间机械臂系统的动力学模型,并通过复合滑模控制方法对轨迹进行振动抑制.Pisculli 等[14]采用有限元法和Newton-Euler 及Euler-Lagrange 的混合方程相结合建立了柔性空间机械臂系统的动力学模型,并采用反应零空间和雅可比矩阵转置控制策略相结合对机械臂系统进行控制.Gao 等[15]利用假设模态法建立了两连杆柔性机械臂的N维离散化模型,并基于全状态反馈控制和输出反馈控制实现了轨迹跟踪和振动抑制.虽然这些控制算法相对成熟,但其依赖于模型的准确程度,较为复杂.由于抗弯刚度、结构阻尼是柔性机械臂的两个主要结构参数,尤其影响弹性振动的响应,因此将结构振动控制方法用于机械臂的振动抑制研究具有重要意义.
结构振动控制方法有被动控制、半主动控制和主动控制三种,其中被动控制和主动控制因外部能源问题而应用受到限制[16].半主动控制仅需较少的能量来调节结构的刚度、阻尼等参数,通过结构的振动能量产生控制力,其控制效果明显优于被动控制,接近主动控制[17].半主动控制主要包括主动刚度控制和主动阻尼控制,刚度主动控制是结构振动控制方法中半主动振动控制技术的常用方法[18-20].目前主动刚度控制在航空航天、微电子机械等技术领域得到一定程度的应用,Lew 等[21]针对地震环境中的结构振动抑制问题,提出了一种结构自适应控制方法,并通过仿真验证了方法的有效性.Li 等[22]提出了一种考虑非线性磁流变阻尼器模型的结构振动半主动控制方法,并采用模糊系统对模型进行逼近,通过控制器对抖振现象进行了控制.Mevada 等[23]研究了被动刚度阻尼器和半主动刚度阻尼器的扭转耦合建筑的地震响应,结果表明半主动刚度阻尼器减小位移和加速度的效果要明显优于被动刚度阻尼器.部分学者对建筑结构层间的主动控制力特征进行研究,研究表明主动控制力除了阻尼项外,主要体现了负刚度控制特性,进而出现了负刚度控制方法[24].汪志昊等[25]对结构振动的负刚度控制进行了详细的研究,为负刚度控制在实际工程中的应用奠定了基础.龚微等[26]基于Benchmark 隔振模型,提出了一种磁流变阻尼器的负刚度智能隔振控制策略,仿真结果表明负刚度控制集合了主动和半主动控制的优点,有效降低地震时隔震层的位移.之后,随着变刚度主动控制算法的不断优化,刚度主动控制得到了广泛应用,耿士能等[27]为避免机械臂碰撞过程中产生冲击与破坏,设计了一种利用温控记忆合金改变关节内摩擦力的变刚度方法,实验结果表明该连续型机械臂具有良好的运动控制精度和刚度调节能力.Petit 等[28]提出了一种多关节变刚度机器人跟踪控制的后退方法,通过对变刚度关节和多关节变刚度机器人进行仿真和测量验证了该方法的有效性.Lin 等[29]提出了采用变刚度的调谐质量阻尼器进行振动控制,数值结果表明该控制方法能够自动避免失调影响并有效抑制振动.
本文根据半主动控制中的变刚度主动控制的设计思想,通过改变机械臂臂杆的轴向受力状况来主动改变机械臂的刚度,进而达到振动抑制的目的,因此文中将该方法称为“臂杆刚度主动控制”方法.在此基础上,采用变形耦合法来计算机械臂的非线性变形,并结合假设模态法和拉格朗日方程建立了臂杆的动力学模型;进而设计了基于臂杆刚度主动控制方法的单自由度实验台,分析了机械臂在不同预紧力下末端的振动特性,结合仿真和实验结果验证了方法的有效性;最后采用响应面法和基于内部映射牛顿法的子空间置信域法优化算法对预紧力进行了优化分析.该研究可为机械臂的精细动力学建模和振动控制提供一定的参考.
1 基于臂杆刚度主动控制的机械臂动力学建模
1.1 臂杆刚度主动控制方法
空间机械臂因臂杆柔性在运动过程中产生的弹性变形与机械臂大范围刚性运动的耦合效应会导致机械臂在其弹性变形中的振动频率不一致,即产生刚化效应.另外,机械臂在旋转运动过程中会受到离心力的作用,轴向的较大变形引起刚度减小,即产生软化效应[30].刚化效应和软化效应相互作用,使机械臂在运动过程中的刚度发生变化,影响其动力学响应.
根据上述机械臂刚度变化效应产生的原理和结构振动控制中的刚度主动控制方法的设计思路,文中提出的臂杆刚度主动控制方法结构示意图如图1 所示.在管状机械臂的臂杆中置一弹性绳索,其两端分别连接拉力传感器与螺栓,拉力传感器用于测量绳索拉力大小,用螺母拧上螺栓以拉紧绳索,通过调节螺栓来调节臂杆受力进而调节臂杆刚度来抑制机械臂运动过程中产生的弹性振动.

图1 机械臂臂杆刚化调节结构图Fig.1 The structure of manipulator arm stiffening adjustment
为建立图1 中机械臂的变刚度动力学模型,将其简化为图2 所示的平面管状悬臂梁模型,虚线为变形前的机械臂,实线为变形后的机械臂.假设机械臂在运动过程中绳索与机械臂始终不接触,因此可将绳索对机械臂的作用力简化为一作用于机械臂末端面的集中力F.另外,机械臂的关节处作用有驱动力矩τ;l0,D0和δ 分别为变形前机械臂的长度、外径和厚度尺寸.为验证臂杆刚度主动控制的效果,在运动过程中同时考虑臂杆的纵向(轴向)变形和横向(径向)变形以及横向变形引起轴向变形的二次耦合效应.

图2 机械臂臂杆刚度主动控制的简化模型Fig.2 The simplified model for active control of manipulator arm stiffness
1.2 臂杆结构参数分析
将臂杆刚度主动控制下的机械臂运动过程进行受力分析,如图3 所示.以机械臂关节端为坐标原点分别建立惯性坐标系OXY和随动坐标系Oxy.机械臂在平面内运动产生刚性转角为θ,F1和F2分别为绳索作用于机械臂末端面的集中力在惯性坐标系中的投影.
设在动坐标系中机械臂上x处任一点P变形前的坐标向量为u0,总变形位移为u,纵向和横向总变形量分别为ux和uv,则

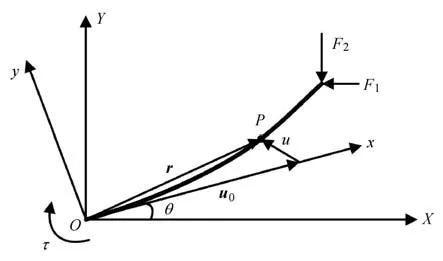
图3 机械臂运动过程中的受力分析图Fig.3 The force analysis during the movement of the manipulator
根据弹性梁的变形理论,考虑完全几何非线性变形,臂杆上P点的纵向和横向变形位移分别为[31]
式中,v1和v2分别为臂杆纵向振动和横向弯曲振动产生的变形;eij为耦合形函数,其表达式为eij=,ϕi(x)和ϕj(x)为臂杆横向弯曲振动的模态函数,qi(t)和qj(t)为与模态函数对应的模态坐标,ε 为积分变量.令vc=,vc为考虑横向弯曲变形引起轴向变形的二次耦合变形量.由此可得
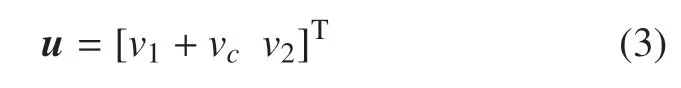
根据臂杆轴向变形和径向变形的关系,可计算得到臂杆变形后的外径D为

机械臂为管状构形,为了保证臂杆结构强度和稳定性要求,臂杆厚度与臂杆外径一般成正比关系

式中,kδ为机械臂截面厚度与外径的比例系数.
结合式(4)和式(5)可计算出变形后臂杆的横截面面积和惯性矩分别为

由式(6)和式(7)可知,机械臂在运动过程中的横截面面积和惯性矩发生变化,引起机械臂在运动过程中的臂杆刚度不断发生变化.
1.3 臂杆动力学模型
如图3 所示,r为臂杆上点P在惯性坐标系OXY中的位置向量,则

式中,r0为点P在动坐标系中的位置向量,分别为动坐标系中u0和u在惯性坐标系中的表示.N为从动坐标系Oxy到惯性坐标系OXY的旋转变换矩阵,即

由规范理论的基本思想,可得如下基本的运动学关系
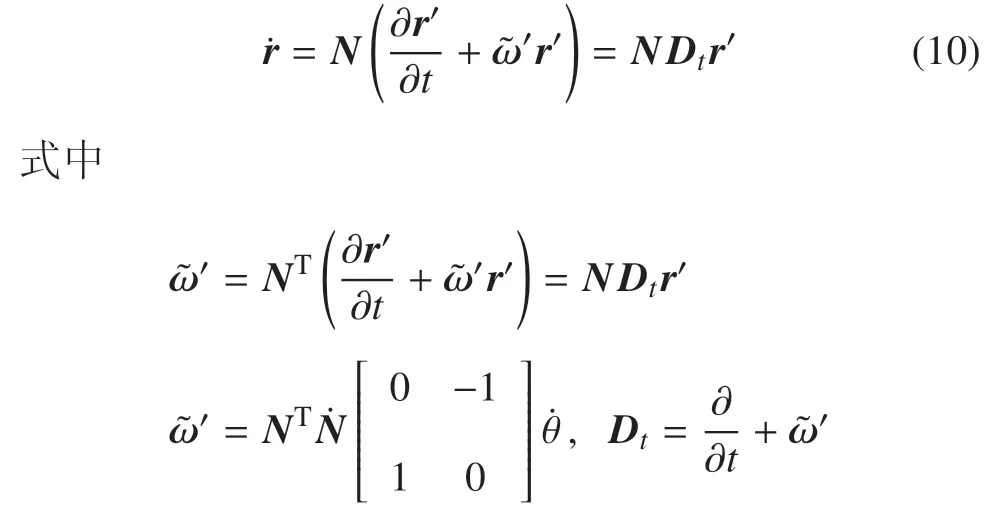
由此可计算出
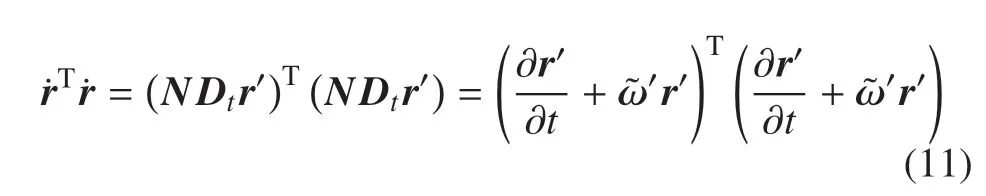
结合式(1)、式(3)及式(8)并考虑,可将上式表示为

基于假设模态法,采用前两阶模态对臂杆的弹性振动进行近似描述,则机械臂的纵向振动和向弯曲振动可表示为
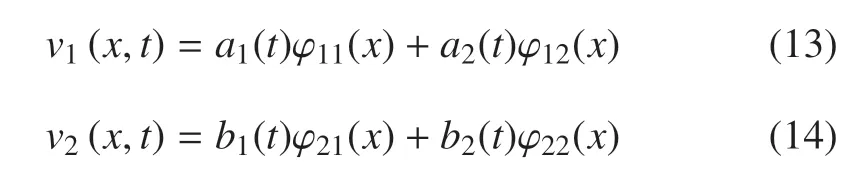
式中,ϕ1i(x)和ϕ2i(x)(i=1,2)分别为机械臂纵向振动和横向弯曲振动的模态函数,ai和bi(i=1,2)分别为与模态函数对应的模态坐标.通过查阅资料可得悬臂梁的前两阶纵向振动和横向弯曲振动模态函数表达式[32]
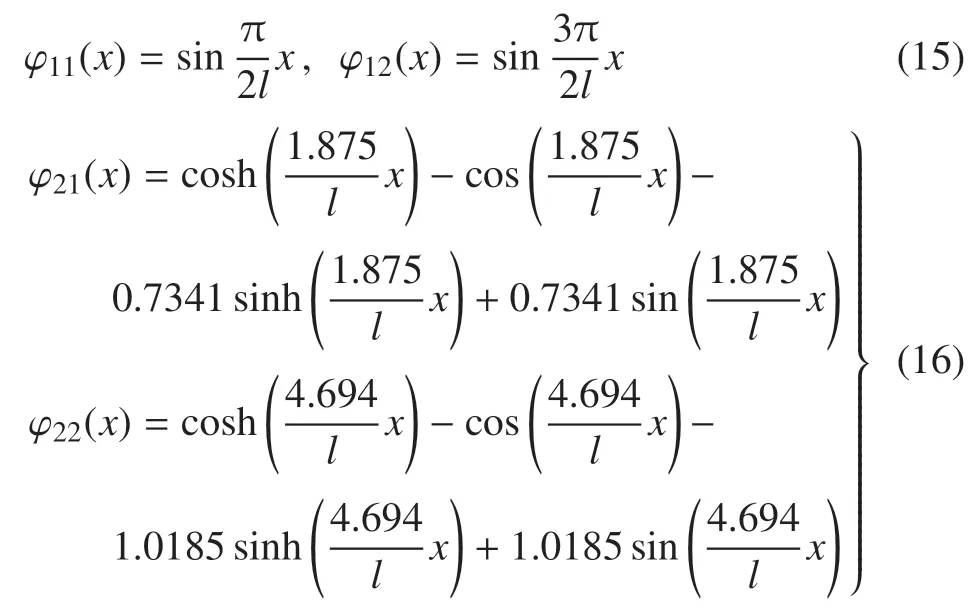
将式(13)~式(16)代入式(12)可得其离散化后的表达式,进而得到机械臂的动能为
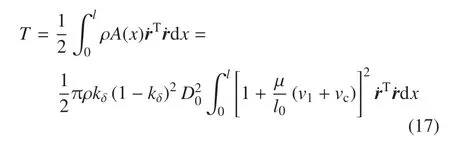
式中,ρ 和µ分别为臂杆的密度和泊松比.由式(17)可知,机械臂系统的动能不仅取决于其刚性运动,还与运动过程中产生的弹性变形密切相关.
机械臂在运动过程中的势能包括弹性势能和重力势能,其中弹性势能包括纵向振动和横向弯曲振动两部分变形能,总弹性势能表达式为
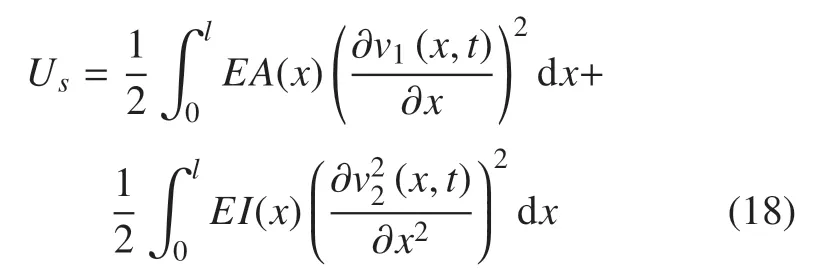
将式(6)和式(7)及弹性变形的离散化表达式(13)和式(14)代入式(18),并取系统的广义坐标为q=[θa1a2b1b2]T,总弹性势能可表示为
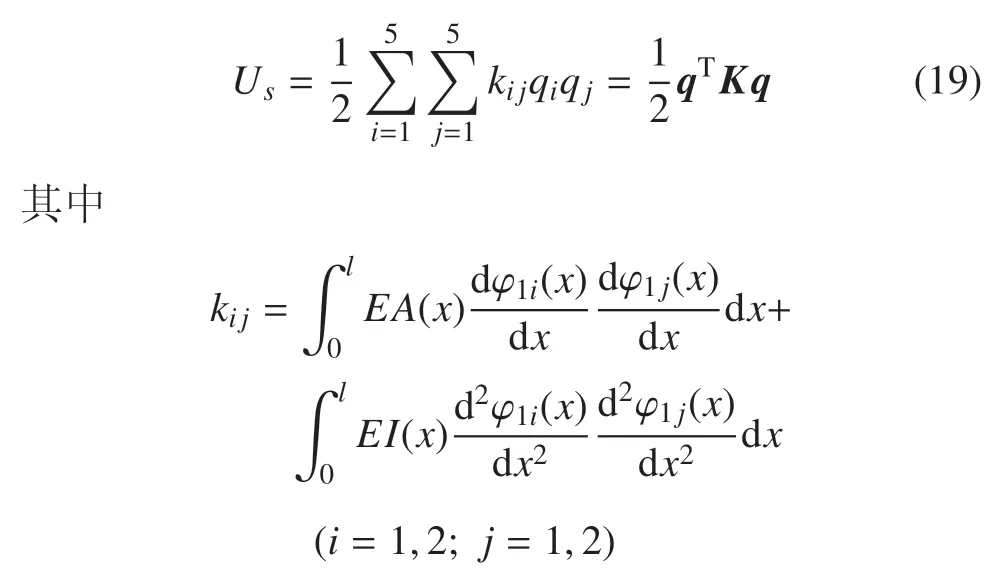
式中,E为臂杆的弹性模量,K为广义刚度矩阵.由刚度矩阵的表达式可知,刚度项中存在纵向变形和横向弯曲变形之间的耦合,且机械臂运动过程中结构参数随臂杆受力发生变化,导致臂杆刚度不断发生变化.同样分析可得重力势能的表达式为
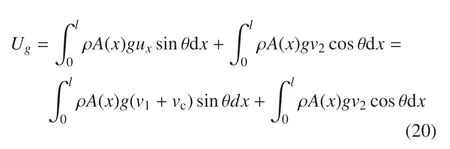
整个机械臂系统所受非保守外力包括关节驱动力矩τ,绳索作用于机械臂末端面的集中力F,根据虚功原理可求得相应于外力的广义力为
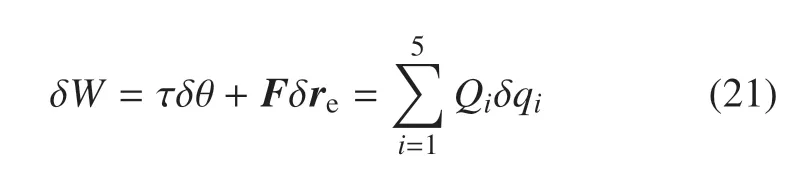
式中,re为机械臂末端点在惯性坐标系中的位置矢量.机械臂末端处变形前位置矢量为uoe=[l00]T,变形总位移为ue=[v1e+vcev2e]T,v1e,vce,v2e分别为机械臂末端处的相应变形量.由此re可表示

设弹性绳索的刚度为k,调节螺栓的移动距离为∆x.由于机械臂在运动过程中绳索与臂杆始终不接触,则绳索作用于机械臂末端面的集中力可表示为

若机械臂末端横向弯曲变形的截面转角为α,则由小变形假设可得到如下近似结果
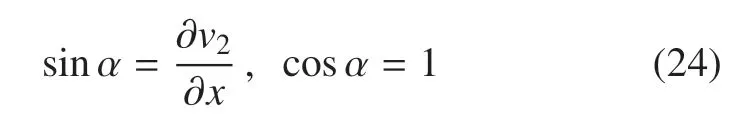
由此可得绳索作用于机械臂末端面的轴向和径向分力大小分别为

将式(22)和式(23)代入式(21)可求得与广义坐标qi对应的广义力大小Qi(i=1,2,···,5).
根据第二类Lagrange 方程

式中,QF=−Kq+Q,Q为上述求得的作用于机械臂上,除变形引起的弹性力以外的全部主动力对应的广义力列阵,−Kq为弹性力对应的广义力.q=[θa1a2b1b2]T为广义坐标列阵,为广义速度列阵.将式(17)、式(19)及式(20)代入式(26)可得机械臂的臂杆变刚度动力学模型为
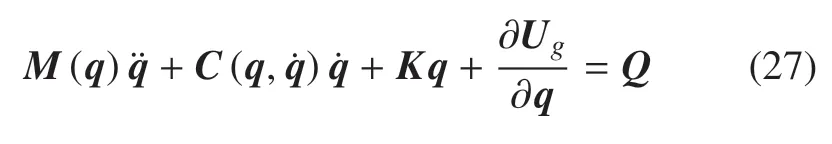
式中,M(q)为5×5 的对称、正定质量矩阵,为包含科氏力、离心力的5 阶列向量,Q为广义力组成的5 阶列向量,M(q),,K(q)均存在纵向变形与横向弯曲变形的耦合项.由此可知,机械臂臂杆的变刚度动力学模型呈现出较强的非线性、强耦合和时变特性.
2 预紧力对机械臂末端振动特性的影响
为了研究机械臂在不同绳索预紧力下的振动特性,对式(27)臂杆的变刚度模型进行了数值仿真求解.系统的结构参数设置如下:l0=0.6 m,D0=0.038 m,kδ=4/38;机械臂的材料参数设置如下:ρ=2.9×103kg/m3,E=68.9 GPa,泊松比µ=0.33;重力加速度为g=9.8 m/s2,机械臂关节的驱动力矩为τ(t)=0.1 sin(2πt)+0.5.仿真初始条件为:q=[0 0 0 0 0]T,˙q=[0 0 0 0 0]T.设置仿真时间为1 s,分别对预紧力为0,10 N,20 N 及30 N 下机械臂末端的振动特性进行了分析,其中预紧力为0 和20 N 时X方向和Y方向加速度曲线及其频谱分别如图4~图7 所示.

图4 预紧力为0 时机械臂末端X 方向加速度及频谱图Fig.4 The X-direction acceleration and spectrum of manipulator end without preloading force
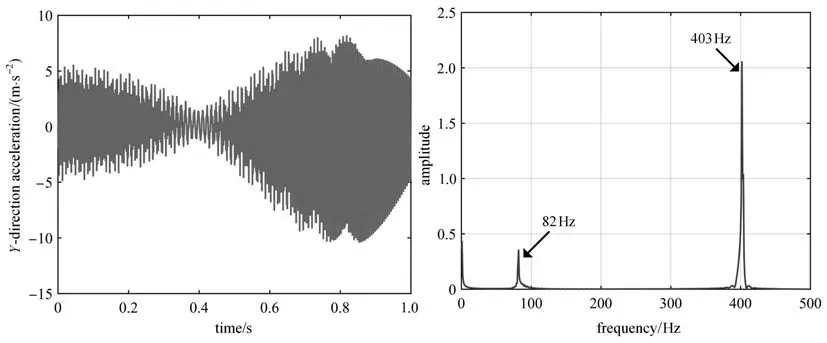
图5 预紧力为0 时机械臂末端Y 方向加速度及频谱图Fig.5 The Y-direction acceleration and spectrum of manipulator end without preloading force
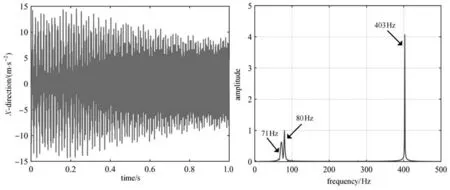
图6 预紧力为20 N 时机械臂末端X 方向加速度及频谱图Fig.6 The X-direction acceleration and spectrum of manipulator end with 20 N preloading force

图7 预紧力为20 N 时机械臂末端Y 方向加速度及频谱图Fig.7 The Y-direction acceleration and spectrum of manipulator end with 20 N preloading force
根据图4 和图5 可知,预紧力为0 时,机械臂末端X方向的加速度振动范围为−15 m/s2~15 m/s2,而Y方向的加速度振动范围为−10 m/s2~8 m/s2,且两个方向的振动能量分别主要集中在82 Hz,403 Hz 两个频率处.由图6 和图7 可知,预紧力为20 N 时,机械臂末端X方向的加速度振动范围为−15 m/s2~15 m/s2,而Y方向的加速度振动范围为−5 m/s2~5 m/s2,两个方向的振动能量分别主要集中在72 Hz,80 Hz,403 Hz 三个频率处.由此可知,随着预紧力的增大,臂杆的低阶频率略微减小,X方向的振动范围影响较小,而Y方向的振动范围明显减小.因此将不同预紧力下Y方向加速度频谱进行对比分析,结果如表1 所示.
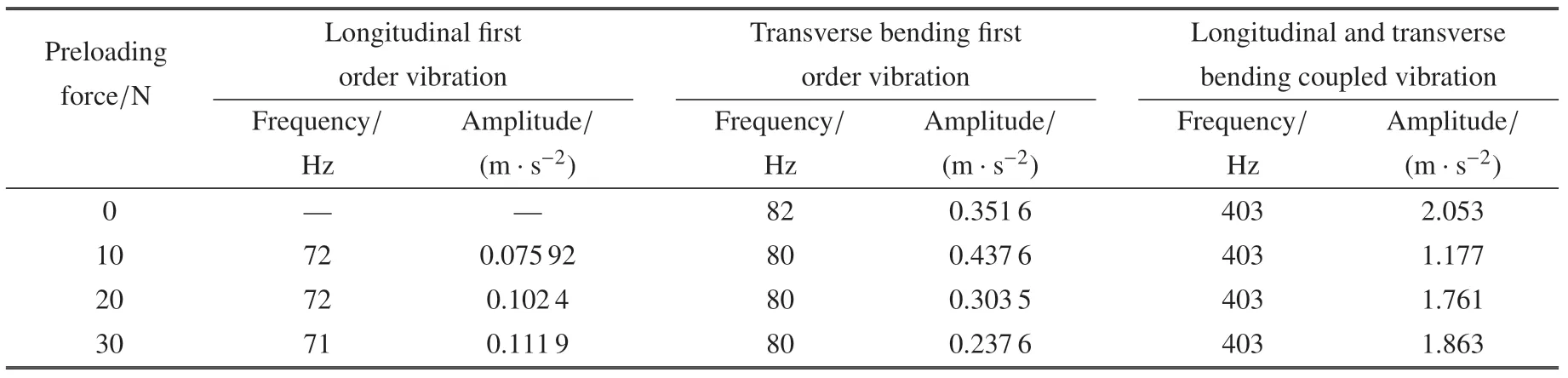
表1 不同预紧力下Y 方向加速度的振动频率及其相应的幅值Table 1 The vibration frequency and corresponding amplitude of Y-direction acceleration under different preloading force
由表1 可知,预紧力存在时,低阶振动频率略微减小,高阶振动频率不变.另外,随着预紧力的增加,纵向一阶振动及纵向和横向弯曲耦合振动的幅值略微增大,而横向弯曲一阶振动略微减小.由于系统的振动能量主要取决于系统的低频振动,而Y方向的振动主要为横向弯曲一阶振动,因此文中提出的基于臂杆刚度主动控制的方法在一定条件下可以抑制机械臂的弹性振动.
3 机械臂臂杆刚度主动控制下的末端振动测试
3.1 机械臂实验台设计
为验证臂杆刚度主动控制对机械臂弹性振动的抑制效果,本文设计了一种平面单自由度机械臂实验台,如图8 所示.该实验台主要包括基座和机械臂主体结构两大部分,其中基座具有90◦的安装可调功能;机械臂的主体结构是臂杆刚化调节机构,主要含有机械臂臂杆、绳索、调节螺栓和加速度传感器等,其调节原理如图1 所示.在机械臂运动过程中,通过调节臂杆内绳索的预紧力来改变机械臂的受力状况,并采用拉力传感器和加速度传感器对绳索预紧力和机械臂末端加速度信号进行实时测量.加速度传感器输入INV-8 多功能抗混滤波放大器中,经过电荷放大器的放大作用将采集到的电信号放大,通过INV3060F 智能信号采集分析仪采集.拉力传感器选用蚌埠金力公司的JL-L 型号,线性度为0.1%,分辨率为2000;加速度传感器选用美国Dytran 公司的压电加速度传感器3056 C,测量频率范围为0~5000 Hz,重量为10 g,灵敏度为15 pC/g,最大加速度可达600 g pk,二者均满足机械臂的测量要求.机械臂关节采用直流伺服电机驱动与谐波减速器传动的形式,臂杆采用铝合金型材,其意义在于研究经济型低刚度材料的刚化问题,以便利用廉价低刚度材料取代目前所应用的昂贵高刚度材料.

图8 机械臂实验装置图Fig.8 The experimental device of manipulator
3.2 机械臂末端振动特性分析
实验过程中保持电机以400 r/min 的转速稳定运行,通过调节绳索预紧力,使臂杆受力分别为0,10 N,20 N,30 N,40 N,50 N,60 N,70 N,测 量 上述8 组绳索预紧力条件下机械臂的振动情况,可得不同预紧力下机械臂末端的加速度信号及其频谱图如图9 所示.

图9 不同预紧力下机械臂末端的加速度响应及其频谱图Fig.9 The acceleration and spectrum of manipulator end under different preloading force
由图9 可知,在不同预紧力作用下,机械臂末端产生剧烈振荡,且加速度信号的振动能量主要集中在0~100 Hz 之间,其中在频率分别为5.8 Hz,16.7 Hz,25Hz 及100 Hz 附近出现4条比较明显的频谱.根据电机的转速计算出其工频为6.67 Hz,而5.8 Hz,16.7 Hz,25 Hz 三种频率与电机工频的倍频接近,且由于机械臂系统各部件运动状况复杂,臂杆刚度随绳索预紧力的变化而发生变化,导致机械臂系统的频率发生变化,因此推测上述3 种频率是由电机工频的倍频引起的.另外,机械臂在各种预紧力下在100 Hz 处都出现幅值突变,而谐波减速的减速比为100,故该频率是谐波减速器与外界激励产生了共振.由以上可知,预紧力的存在对臂杆刚度影响较小,但可以使机械臂末端的振动得到一定的衰减.不同预紧力下机械臂末端振动幅值变化范围如表2 和图10 所示.

表2 不同预紧力情况下臂杆末端振动幅值的变化范围Table 2 The range of vibration amplitude of manipulator end under different preloading force

图10 机械臂末端振动幅值随预紧力的变化曲线Fig.10 The curve of vibration amplitude of manipulator end with preloading force
结合表2 和图10 可知,随着绳索预紧力的增加,机械臂的振动幅值变化范围呈现收拢趋势,且上限幅值和下限幅值的大小几乎都随着预紧力增加而减小.说明文中提出的臂杆刚度主动控制方法在一定条件下可以有效抑制机械臂末端的弹性振动.
4 预紧力的优化分析
绳索预紧力越大,会导致机械臂存在较大内应力,影响其结构性能,而实际机械臂在不同工况下需要满足不同的功能要求和精度要求,因此需要选择既满足精度要求又保证结构性能要求的预紧力,而不是无限增大预紧力.为了获取预紧力与机械臂末端振动响应的关系,采用响应面法来近似表示系统的极限状态函数[33].为反映机械臂末端的振动剧烈程度,选择臂杆末端的振动幅值范围来表示性能函数,即

式中,φ 为极限状态函数,u和d分别上限幅值和下限幅值.为准确获得极限状态函数,采用二次多项式来近似表示性能函数,即
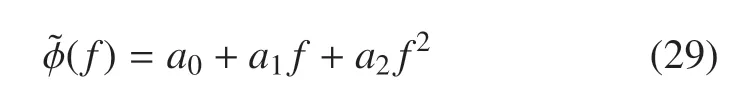
式中,f为预紧力的大小,a=(a0,a1,a2)T为回归系数的矢量.
结合表2 不同预紧力下机械臂末端振动的上限幅值和下限幅值,可得响应面函数的设计点和响应点如表3 所示.
根据式(29)所示的响应面函数和表3所示的设计点及响应值,可以求得回归系数a,并由此可得响应面函数为
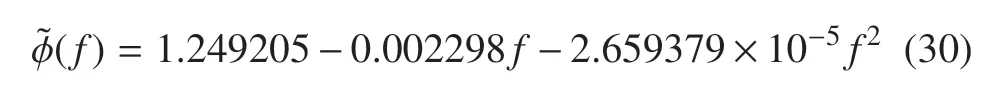
基于内部映射牛顿法(interior-reflective Newton method)的子空间置信域法(subspace trust-region)优化算法对式(30)的响应面函数进行寻优处理,将预紧力作为设计变量,机械臂末端振动最小化作为目标函数,建立数学模型为
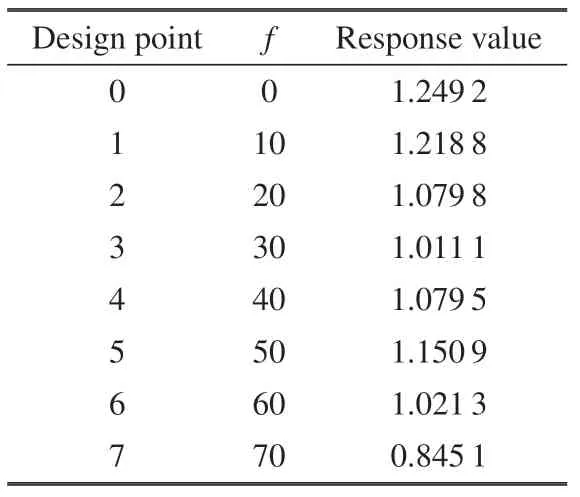
表3 响应面函数的设计点和响应值Table 3 Design points and response values of the response surface function

根据式(31)获得的最优预紧力的大小为70 N,如图11 所示.说明在本文实验条件下,预紧力为70 N 时,机械臂末端的振动得到最大衰减,可以获得较高的末端精度.

图11 预紧力与响应值关系曲线Fig.11 The curve of preloading forces and response values
5 结论
为抑制机械臂在运动过程中因臂杆柔性引发的结构变形和弹性振动,本文提出了臂杆刚度主动控制方法.采用变形耦合法研究了机械臂运动过程中臂杆径向弯曲变形对轴向变形的影响,并基于假设模态法对柔性机械臂进行离散化描述,结合Lagrange 方程建立了臂杆的变刚度动力学模型.在此基础上,设计了基于臂杆刚度主动控制方法的单自由度实验台,通过调节臂杆内绳索预紧力来调节臂杆刚度,研究了机械臂在不同预紧力下末端的振动特性.实验和仿真结果表明,随着预紧力的增加,本文提出的基于臂杆刚度主动控制的方法可以有效抑制机械臂末端的振动,提高机械臂的运动稳定性和末端定位精度.采用响应面法建立了机械臂末端的振动响应与预紧力的关系,并基于内部映射牛顿法的子空间置信域法优化算法得到了响应面内的最优预紧力.该研究可为机械臂的精细动力学建模提供一定的理论参考,并为研究经济型低刚度材料的刚化问题提供了方向,以利用廉价低刚度材料取代目前所应用的昂贵高刚度材料.

