基于FPGA的动态脉宽调制研究

刘永峰，迟耀丹，赵 阳，王立光，吴博琦

吉林建筑大学 电气与计算机学院,长春 130118

0 引言

交流电机在工业和民用行业中都是最主要的拖动设备,电机通常需要进行调速以满足不同产品需求和用户需求.随着科技发展,电机调速方式经历了机械式有级调速、电气与机械配合的有级调速和变频调速三个阶段[1],而且随着需求不断升级,前两种方式已经不能满足复杂的产品需求,变频调速方式成为更多用户的选择.自20世纪80年代起变频器实现商业化,变频调速技术从模拟控制、数模混合控制,逐渐发展到数字控制,变频技术不仅使驱动变得交流化,而且是呈现数字化、高频化以及智能化[2]的发展趋势.

1985年Ross Freeman发明了现场可编程门阵列(Field programmable gate array,英文缩写为FPGA),既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点,逐渐成为各种定制芯片的替代品[3].FPGA技术的开发本质是逻辑电路的实现,在一些高灵活性、高性能、定制化程度高的场合,是设计者的最优选择.FPGA相比于其他芯片的最大特点是灵活性和并行性,灵活性在于产品升级不仅限于产品设计阶段,整个生命周期内都可以进行更新升级,并行运算能力表明完成相同的控制流程,FPGA处理时间更短,有更好的实时性.

1 脉冲宽度调制技术

脉冲宽度调制(Pulse width modulation,英文缩写为PWM)技术是逆变系统中的关键技术,其本质在于优化开关函数,使得逆变器按一定规律输出电压[4],脉宽调制方式对电机的调速性能有着决定性影响.自德国学者A-Schonung提出脉宽调制变频思想以来,已经发展出了几十种脉宽调制技术[5].正弦脉宽调制(Sinusoidal pulse width modulation,英文缩写为SPWM)是目前最成熟的调制方法,以高频三角波作为载波,与期望波形同频的正弦波作为调制波,由调制波与载波相交点确定逆变器开关器件的导通时刻,根据面积相等原则,获得等幅不等宽的等效矩形波.

与SPWM不同,空间矢量脉宽调制(Space vector pulse width modulation,英文缩写为SVPWM)是针对交流电动机变频驱动提出的脉宽调制方法,从三相输出电压整体效果出发,通过改变逆变器开关器件通断状态使实际磁通逼近理想圆形电机气隙磁通轨迹,其基本原理是:用若干个开关电压矢量去逼近某一时刻的空间电压矢量[6].

与SPWM相比,SVPWM技术能有效减少绕组电流谐波成分,降低电机转动脉冲,转子旋转磁场更接近圆形,是一种理想的脉宽调制方法.近年来,FPGA为电机调速系统数字化提供了新的实现方式,当前大多数控制系统选择FPGA与数字信号处理(Digital signal processing,英文缩写为DSP)结合控制的方式,这种方式在高速通讯过程中会不可避免的出现时序混乱、电磁干扰等问题.

本文研究基于FPGA的空间矢量脉宽调制方法,可有效解决上述问题,输出理想PWM波形,实现交流电机调速功能.

2 空间矢量脉宽调制(SVPWM)调制原理

空间矢量脉宽调制主要思想在于通过不同逆变器空间电压矢量的切换以获得恒定圆形磁场[7],通过三相逆变器开关状态的切换,产生PWM波,使逆变器输出的电流波形尽可能接近理想正弦波.图1为三相桥式逆变器与永磁同步电机的连接图,三相逆变器输出相电压分别为UA,UB,UC,定义其空间电压矢量为UA(t),UB(t),UC(t),方向在各自的轴线上,大小随时间按正弦规律变化,时间相位上相差120°.三相电压空间矢量的合成矢量U(t)的表达式如下:

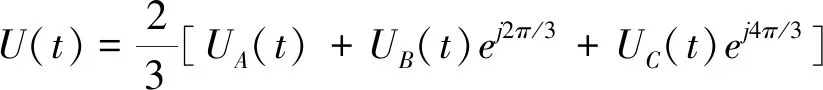
(1)

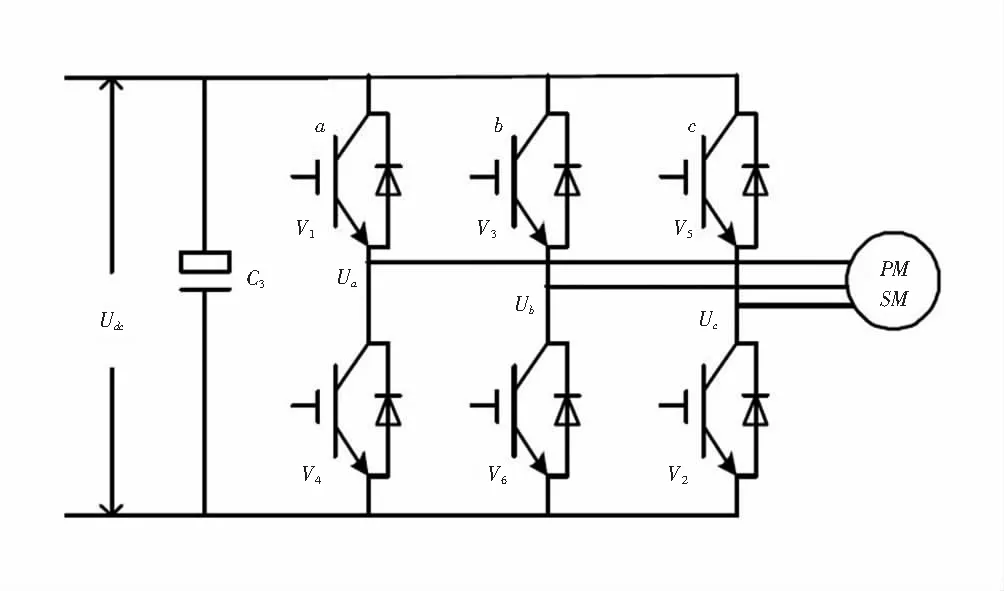
图1 逆变电路Fig.1 Inverter circuit

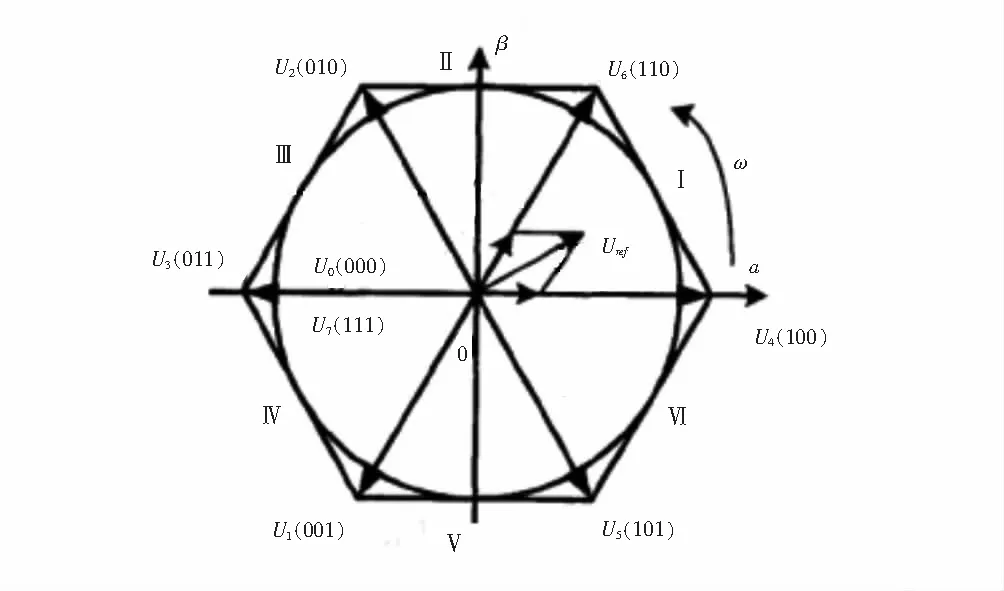
图2 电压矢量分布Fig.2 Voltage vector distribution

如图1所示,Udc为直流母线电压,以A相为例,SA=1时,UA(t)=Udc,Ua,Ub,Uc为逆变器输出端相电压,V1～V6为逆变器三相桥臂的开关器件.三相桥式逆变器上桥臂与下桥臂开关器件状态互补,定义Sx=1,Sx=0(x=a,b,c)为各相上桥臂开关器件的通、断状态,用(Sa,Sb,Sc)表示逆变器的8种开关状态,对应8个电压矢量,其中6个有效电压矢量(001),(010),(011),(100),(101)和(110),2个零矢量(000)和(111),输出电压可用式(2)计算:

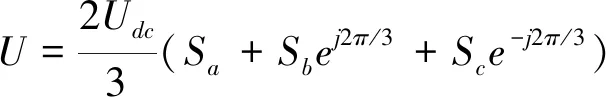
(2)

如图2所示，6个等幅非零矢量和2个零矢量将空间分为6个扇区,扇区内的任意电压可由相位依次相差60°的基本电压矢量合成,2个零矢量位于扇区中心,非零矢量模值为:

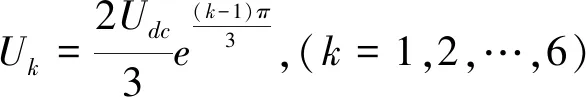
(3)

逆变器参考电压矢量Uref由其所处扇区相邻基本电压矢量和零矢量合成,在一个PWM周期Ts内,根据伏秒平衡原理[8]有:

TSUref=TkUk+Tk+1Uk+1+T0U0+T7U7

(4)

TS=Tk+Tk+1+T0+T7

(5)

式中,Uk,Uk+1表示扇区相邻电压矢量;U0，U7为零矢量;Tk,Tk+1,T0和T7为对应电压矢量作用时间.在SVPWM调制方案中,适当使用零矢量可减少开关动作次数,做到跨越相邻扇区只需要调整一相开关状态,大幅度减少开关损耗,零矢量动作时间的平均分配有效降低了PWM的谐波分量.整理式(4)有:

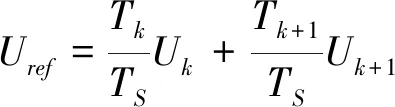
(6)

对于任意Uref在α,β坐标系中均可被分解为Uα和Uβ,即Uref=(Uα+jUβ),结合式(3)、式(6)可得相邻电压矢量作用时间,公式如下:

(7)

Tk,Tk+1的取值只有3种情况：

令：

零矢量作用时间为：

T0=T7=1/2(TS-Tk-TK+1)

3 Matlab/Simulink仿真实现

本文基于Matlab/Simulink平台进行SVPWM算法仿真实验,如图3所示，SVPWM算法仿真由Clarke变换、扇区判断、电压矢量作用时间和开关切换时刻等模块组成,通过波形发生器模块产生的同频等幅相位相差120°三相交流电经过坐标变换和计算后与PWM载波进行比较,输出PWM波形.

仿真电路输出的 PWM 控制信号波形如图 4 ～ 图 5所示,通过 Matlab/Simulink 平台对控制系统进行的仿真实现表明,三相逆变器的SVPWM算法对在调速方面的适用性和正确性,值得注意的是6路PWM波中每一相的两路PWM波形彼此互补如同一时刻PWM 1和PWM 2波形电平正好相反.

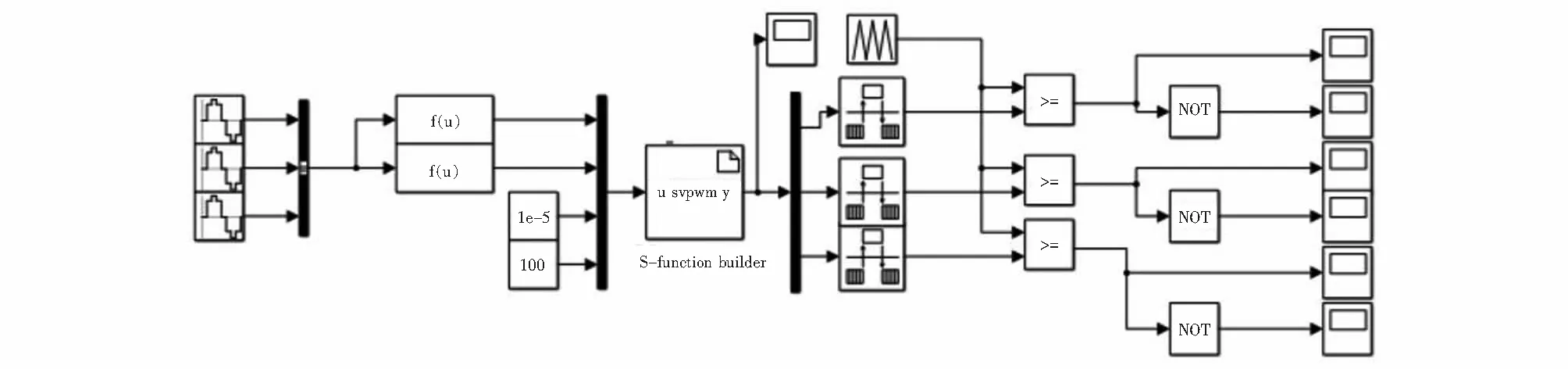
图3 SVPWM算法仿真图Fig.3 Simulation diagram of SVPWM algorithm

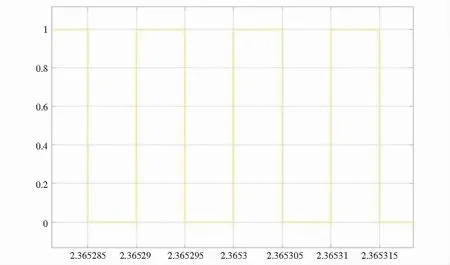
图4 PWM 1输出波形Fig.4 PWM 1 output waveform

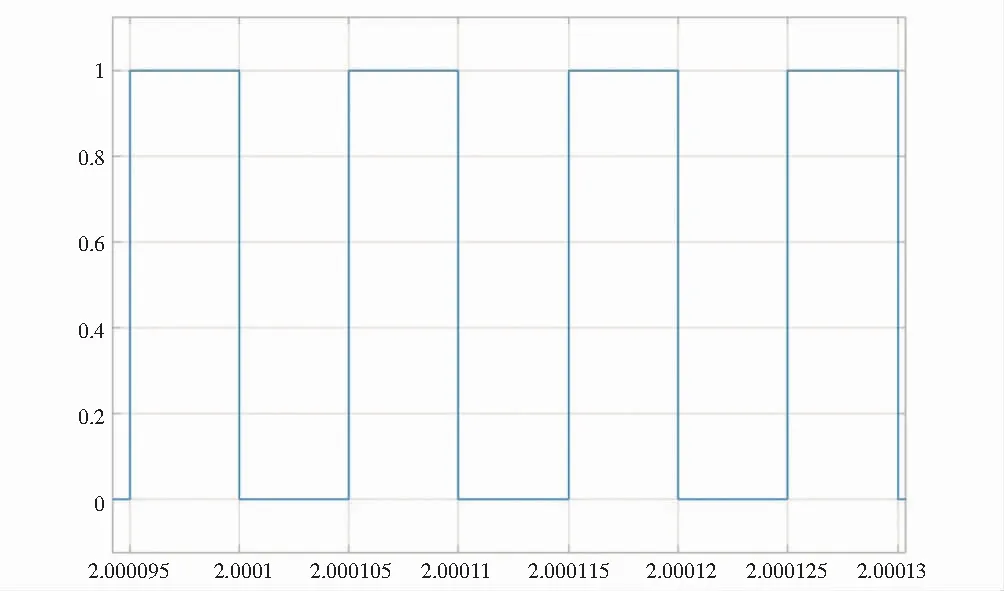
图5 PWM 2输出波形Fig.5 PWM 2 output waveform

4 基于FPGA的SVPWM实现

SVPWM技术本质上是通过控制逆变器6个开关器件的通断输出可调PWM波形,控制算法较复杂,控制系统对控制器的处理能力有较高要求.本文采用Xilinx公司的Spartan - 6芯片作为数字控制器,Spartan系列是Xilinx公司推出的低成本高容量FPGA,内部采用双寄存器和具有AES和Device DNA保护的加强IP[9],FPGA展现出的可重构、可并行运算能力受到设计者的青睐,成为众多设计者的首选.本文基于Xilinx公司的FPGA芯片在ISE 14.7环境下编程,采用模块化编程方法实现SVPWM算法,分为三相电压坐标变换、参考电压矢量扇区判断、电压矢量作用时间计算和逆变器开关切换时间计算四个模块完成脉宽调制任务.

图6 FPGA实现SVPWM总体框图Fig.6 FPGA implementation of SVPWM block diagram

4.1 Clarke坐标变换

三相交流电经Clarke变换后将三相电压Ua,Ub,Uc在(a,b,c)坐标系中的变化转化到两相(α,β)坐标系中,用Uα,Uβ表示.

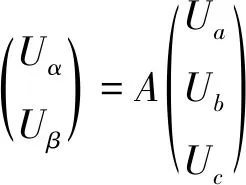
Ua=Uα

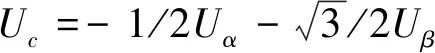
(8)

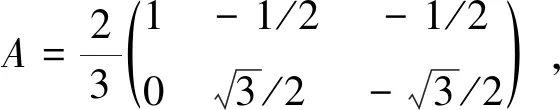
4.2 扇区判断

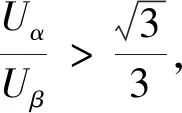
表1 扇区-P值对照Table 1 Sector-P value comparison

简化后的扇区判断方式使系统在运算量会运算速度方面有明显改善.

4.3 相邻电压矢量作用时间

由于基本电压矢量模值恒定,逆变器输出矢量电压的改变取决于电压矢量作用时间,根据式(7)可计算出在各扇区内相邻电压矢量作用时间如表2所示.

表2 相邻电压矢量作用时间Table 2 Action time of adjacent voltage vectors

SVPWM调制模式下,最大空间电压合成矢量的运行轨迹为图2扇区六边形内切圆,零矢量作用时间为零时Uref模值最大,当Tk+Tk+1>TS,表明合成电压矢量发生过调,为避免波形失真,本文采取比例缩小算法进行调制处理,设Tk′,Tk+1′为Tk,Tk+1调整后使输出波形不失真的值,满足如下关系:

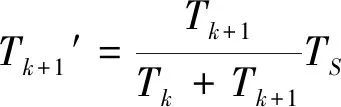
(9)

经式(9)变换等比例缩短有效电压矢量作用时间,使合成电压矢量回归到理想轨迹.

4.4 开关状态切换时间

直接数字式频率合成器(DDS)是一种常见的波形发生方式,占用资源少,硬件语言简单,改变参数设置可以方便地获得常见的正弦波、方波和三角波[10].本设计PWM载波由DDS产生,三角波波形产生代码如下:

reg[15:0] tcnt;

reg[8:0] tringle_tmp;

reg[7:0] tringle_wave;

always@(posedge clk or negedge rst_n)

if(!Rst_n) tcnt<=16’d0;

else if(tcnt<16’d48827) tcnt<=tcnt+1’b1;

else tcnt<=16’d0;

always@(posedge clk or negedge rst_n)

if(!rst_n) triangle_tmp<=9’d0;

elseif(tcnt==16’d48827) triangle_tmp<=triangle_tmp+1’b1’

always@(posedge clk or negedge rst_n)

if(!rst_n) triangle_wave<=8’d0;

else if(triangle_tmp<9’d256) triangle_wave<= triangle_tmp[7:0];

else triangle_wave<=～triangle_tmp[7:0];

逆变器开关导通时刻计算公式如下:

Ta=(TS-Tk-Tk+1)/4

Tb=Ta+Tk/2

Tc=Tb+Tk+1/2

(10)

Ta,Tb,Tc为开关管导通时刻,与导通时间赋值方式类似,根据不同扇区进行分配,定义Taon,Tbon,Tcon为采样周期内每一相触发时刻,不同扇区内A,B,C三相开关导通时刻按表3进行赋值.

表3 开关切换时间赋值Table 3 Switching time assignment of the switch

将Taon,Tbon,Tcon分别存入FPGA的3个寄存器单元中.电压矢量在每个载波周期内逆时针旋转一个固定角度,旋转角度大小由载波频率和PWM频率共同决定,基本电压矢量作用时间在每个载波周期重新计算并合成空间电压矢量,通过不断合成新矢量的方式,期望电压矢量依次经过各扇区,逆变器输出理想电压波形.为避免载波与调制波多次相交产生窄波,规定三角波上升或下降过程只有第一次相交时改变调整PWM波形的电平,其余时间保持相应电平.

5 结语

本文详细阐述了SVPWM调制原理,提出一种基于FPGA动态脉宽调制方法,从系统性能角度分析基于FPGA实现SVPWM调制算法的优势,并进行Matlab/Simulink仿真实验.结果显示,SVPWM调制模式下逆变器输出最大不失真电压矢量模值约为0.58Udc,比传统SPWM调制方式在电压利用率方面高出约15.5 %.基于FPGA的SVPWM调制方式使得全数字交流变频调速系统开发灵活、硬件利用率更高、算法实现更加清晰,卓越的并行运算能力缩短了系统数据处理时间,提高系统的控制能力,FPGA的现场可编程能力,在有效提升控制系统性能的同时降低了系统二次开发成本,保证系统具有良好的可维护性.