基于Adams建模的风电机组齿轮箱故障特征提取*

安志龙 马 丽 董唯光

（1.陕西铁路工程职业技术学院 渭南 714000）（2.兰州交通大学 兰州 730070）

1 引言

风电机组中齿轮箱的主要作用是传递扭矩和增速，它是风电机组中的关键部件。然而，风力发电机组工作在室外恶劣环境中，由于载荷和风速的突变，风机极易出现故障。据统计，增速齿轮箱在整个传动系统中发生故障的概率最高，研究适合风电机组特点的在线故障监测和故障诊断方法是目前亟需解决的问题之一［1～3］。

目前，国内关于风电机组齿轮箱的故障诊断研究方兴未艾，文献［3］通过在刚体动力学模型中引入柔性体，进而对行星齿轮进行刚柔耦合仿真，分析了断齿故障特征和对应的故障频率。文献［4］以SIMPACK多动力学仿真平台，结合ANSYS有限元分析和GH Bladed载荷计算软件，建立风电齿轮箱传动系统全柔性体模型，得到了系统固有频率、能量分布图、速度加速度等振动信号。文献［5］研究兆瓦级水平轴风电机组传动系统，并基于多体系统和集中参数法建立了精细的风机传动系统动力学模型，为模拟风电传动系统的优化设计提供了理论依据。文献［6］建立两级行星轮加一级平行轴传动的齿轮箱虚拟样机模型，通过ADAMS动力学分析软件，分析齿轮啮合力在传动过程中的变化规律。文献［7］基于流形学习算法提出一种早期故障预警方法，该方法结合完全总体经验模态分解和改进快速独立成分分析盲源分离技术，提取了风电机组的早期故障敏感特征。文献［8］通过EMD分解故障振动信号，为获取高维特征向量进行熵值构造，利用正交领域保持嵌入进行特征降维，最后用隐Markov实现旋转机械的故障识别。文献［9］提出一种基于流形学习的风电机组齿轮箱故障诊断模型，ADAMS对齿轮箱建模并分析正常与故障状态下的振动信号，通过流形学习算法降维并实现齿轮箱的故障诊断。行星齿轮传动普遍用于机械传动的各领域中，主要原因是其结构紧凑、传动平稳和传动比大等优点。齿轮箱内齿轮的主要故障形式有轮齿断齿和齿面点蚀、剥落、磨损等；轴承的故障主要表现为轴不对中和滚珠磨损、点蚀、破损等［9～10］。

文献［12］在Adams/Vibration模块中建立发电机悬置系统动力学模型，并求解固有频率和模态能量。文献［13］通过多体动力学仿真平台建立了齿轮箱传动系统仿真模型，分析了系统的固有频率及各频率下的角加速度振动信号。上述文献仿真过程均未体现故障建模及仿真，因此本文分别建立正常和故障下的齿轮箱仿真模型，为齿轮箱故障诊断分析提供了依据。通过UG软件创建了完全参数化的风电机组齿轮箱三维实体模型，其参照1.5MW风电机组参数，建立结构为两级行星轮加一级平行轴的齿轮箱模型。在Adams中导入所建模型，为了得到风电机组齿轮箱虚拟样机模型，需要添加固定副、旋转副、接触副和构件属性信息。在Adams中对齿轮箱进行故障建模及分析，提取齿轮箱在正常、断齿、轴不对中三种情况下的振动信号，并用EMD方法将其分解成若干个平稳的本征模态函数IMF，实现风电机组齿轮箱的故障特征提取。

2 风电机组齿轮箱建模及仿真分析

2.1 风电机组齿轮箱建模

文章建立了1.5MW风电机组齿轮箱两级行星轮加一级平行轴结构的仿真模型，如图1所示，其中上图为带壳的齿轮箱整体模型，下图为隐藏齿轮箱外壳后结构为两级行星轮加一级平行轴的齿轮传动模型。其传动路线：1）低速级：主传动轴→行星架→行星轮→太阳轮→2）中速级：行星架→行星轮→太阳轮→3）高速级：主动大齿轮→从动小齿轮［9］。依据1.5MW风电机组齿轮箱的建模参数，如表1所示，在UG中创建齿轮箱三维实体模型，并以扩展名为.x_t的格式导入Adams，完成风电机组齿轮箱虚拟样机模型的建立。根据风电机组实际运行状况添加三种约束副（maker）并各自命名：1）旋转副：主轴+固定地、太阳轮+固定地、行星轮+行星架、输出级齿轮+固定地；2）接触副：各行星轮+太阳轮、各行星轮+内齿圈、输出级主动轮+从动轮；3）固定副：主轴+低速级行星架、低速级太阳轮+中间级行星架、内齿圈+固定地。

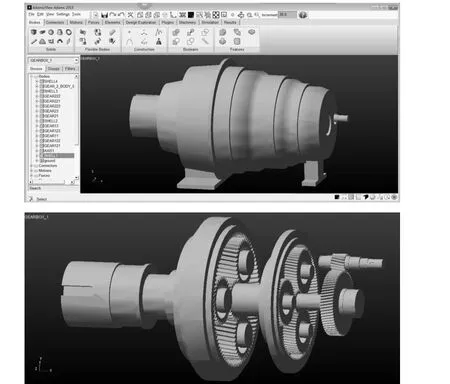
图1 风电机组齿轮箱仿真模型

2.2 齿轮箱仿真分析

为模拟齿轮箱正常运行，对齿轮箱虚拟样机模型输入轴施加恒转速135°/s，得到输入轴角速度曲线如图2所示，输出轴角速度曲线如图3所示，低速级太阳轮角加速度曲线如图4所示，中速级角加速度曲线如图5所示。

从图2可以看出齿轮箱在运行0.2s后，输入轴角速度曲线可达到稳定值135°/s。图3可以看出齿轮箱在运行2.4s后，输出轴角速度曲线能够趋于稳定值，说明该齿轮箱虚拟样机模型运行效果良好，所建模型具有可行性与研究性。从图4和图5可以看出齿轮箱运行初期，两级太阳轮角加速度时域波形的随机信号特征较明显；当运行稳定后，曲线波动逐渐平稳，幅度变换逐渐趋于均匀，表明该模型运行状态稳定。我们已知，在输入轴加以稳定的转速，模型输出部分也应能达到稳定值，所以从输入轴角速度曲线和输出轴角速度曲线验证了该模型的准确性。

表1 风电机组齿轮箱建模参数

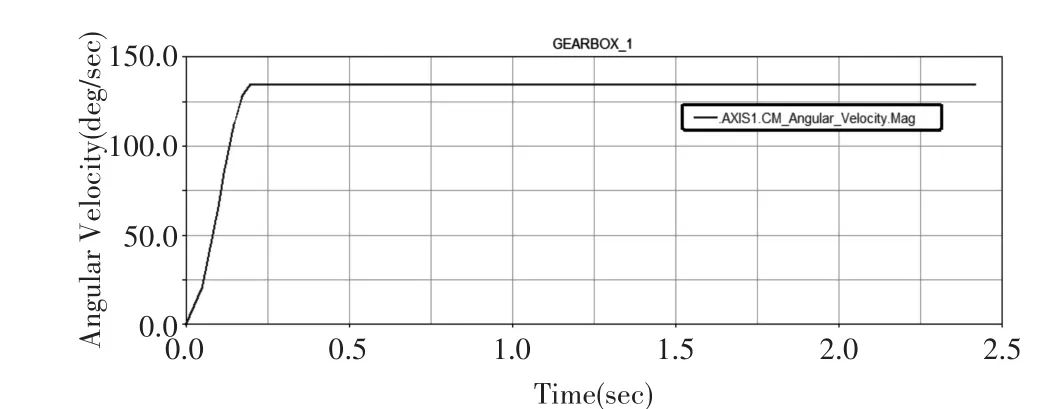
图2 输入轴角速度曲线

图3 输出轴角速度曲线

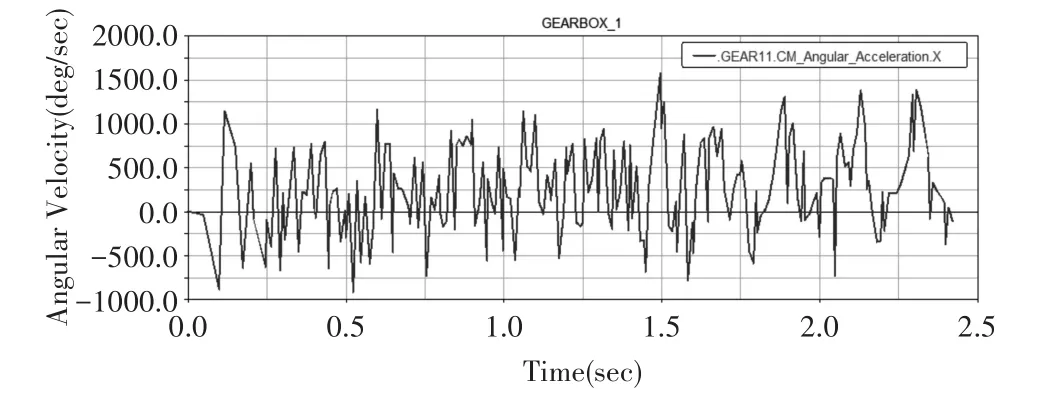
图4 低速级太阳轮角加速度曲线

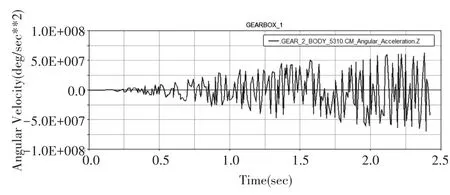
图5 中速级太阳轮角加速度曲线

3 风电机组齿轮箱故障仿真建模

3.1 断齿故障

为了模拟齿轮箱断齿故障，在Adams中通过模型修改功能对正常状态下的两级行星轮加一级平行轴齿轮箱进行断齿修改，为高速级从动小齿轮建立轻微断齿和严重断齿故障的仿真建模，其中轻微齿模型如图6所示，严重断齿模型如图7所示。

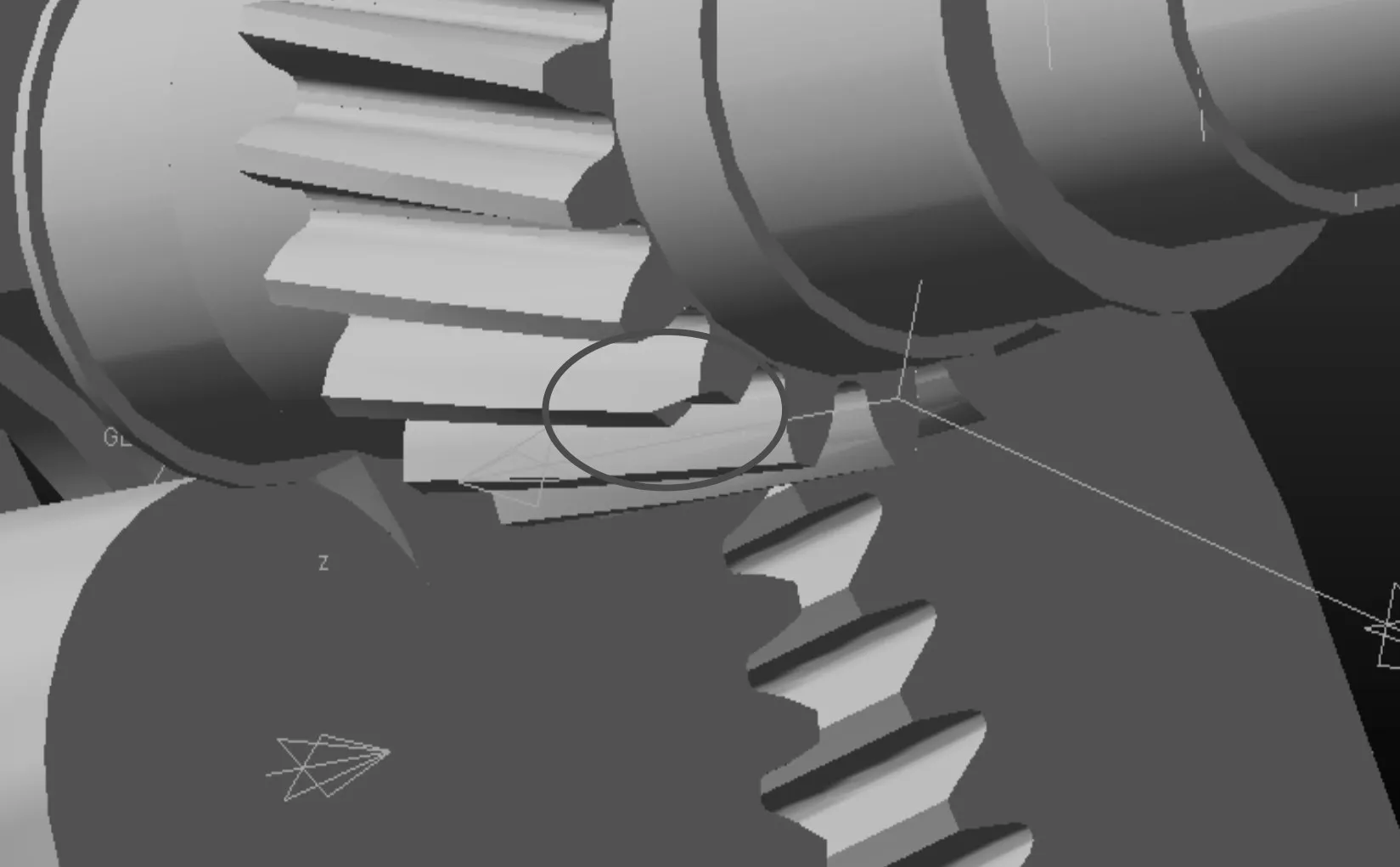
图6 齿轮箱轻微断齿模型

图7 齿轮箱严重断齿模型

3.2 轴不对中故障

当齿轮箱发生轴不对中故障时，选取轴心分别偏离几何中心1mm和0.5mm的故障进行模拟。为了验证轴不对中故障的发生，将单位正弦激励分别施加在正常模型和故障模型的输入端X轴方向，得到输出轴分别在X，Y，Z三方向的加速度频率响应曲线，如图8、图9所示。对于正常的齿轮箱，当正弦激励施加在输入端X轴方向时，其加速度频率响应变化：X轴响应不变，Z、Y轴发生变化；对于故障的齿轮箱，当正弦激励施加在输入端X轴方向时，其加速度频率响应变化：X、Y轴方向均呈增大趋势，Z轴方向，以100Hz为界限，先增大，后稳定。通过比较1mm和0.5mm两种程度故障，发现输出轴加速度频率响应随不对中程度的增大而增大。

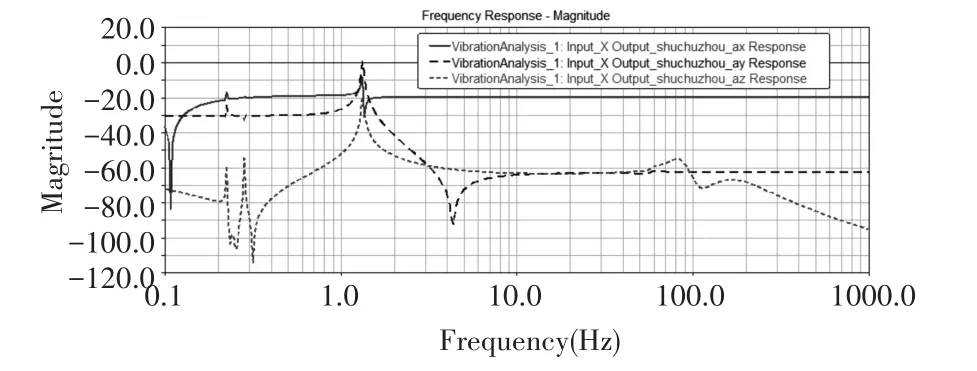
图8 正常情况下X轴方向给激励时输出轴加速度响应曲线

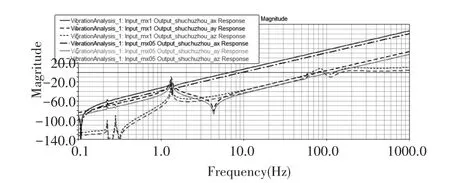
图9 轴不对中情况下X轴方向给激励时输出轴加速度响应曲线

4 风电机组齿轮箱故障特征提取

在分析处理非线性、非平稳信号时，经验模态分解（Empirical Mode Decomposition，EMD）方法有独到之处。该方法的基本原理是通过分析复杂信号本身所具有的不同特征尺度或不同波动趋势，将信号按照这些尺度或趋势的特点层层逐级分解，实现复杂信号的平稳化处理［14］。使用若干个平稳的本征模态函数（Intrinsic Mode Function，IMF）来表达一个复杂非平稳的信号，而各IMF分量都具有原始信号的不同局部特征。那么，现在的关键问题是如何确定分解得到的分量就是我们所求的本征模态函数IMF？Norden E.Huang博士解答了这个问题：

1）分解所得各分量的极大值点和极小值点的数目与过零点的数目相等或者最多仅相差一个［14～15］；

2）各分量中由局部极大值点勾勒出的上包络线与局部极小值点勾勒出的下包络线的平均值为零［14～15］。

满足以上两个条件的分量就是我们所求的IMF分量。因为原信号的不同时间尺度特征或不同波动趋势主要是由各个极值点之间的间隔来表现的，所以EMD分解得到的本征模态函数IMF务须满足上述的两个条件［16］。现假设我们要分析的信号是x(t)，EMD分解步骤如下。

首先，通过对信号x(t)的极值点序列进行三次样条函数插值，得到上包络线u1(t)和下包络线v1(t)，假设包络线均值为m1(t)，则m1(t)表示为

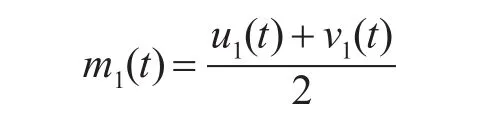
然后，用原信号x(t)减去包络均值m1(t)，假设所得新序列为h1(t)，表示如下：

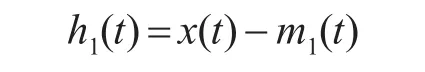
根据IMF必须满足的两个条件，判断新序列h1(t)是否满足。若满足，则记h1(t)为第一个IMF分量，若不满足，则重复上述过程，得到h1(t)的包络均值m11(t)，如下：

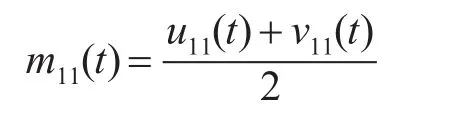
用h1(t)减去包络均值m11(t)，得到新序列h11(t)，如下：

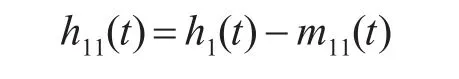
根据IMF必须满足的两个条件，判断新序列h11(t)是否满足。若满足，则记h11(t)为第一个IMF分量，若不满足，则再次重复上述过程，重复k次，直到得到一个满足条件的序列为h1k(t)：

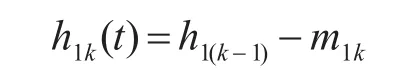
那么，我们所要求解的第一个本征模态函数IMF就为h1k(t)，记为c1(t)=h1k(t)。

从原信号x(t)中分解出c1(t)，残余信号表示为r1(t)，即：

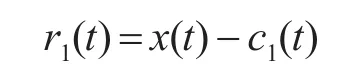
将r1(t)作为新的原始信号，重复以上过程，直到得到c2(t)，从中分解c2(t)，得到新的残余信号r2(t)，再次重复上述过程，直至最后得到一个单调的残余项rn(t)。此时，原信号就x(t)被分解成n个本征模态函数c1(t)，…，c1(t)和一个残余项之和，其表示如下：

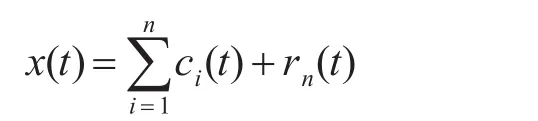
式中ci(t)表示原信号x(t)的第i个本征模态函数IMF，分解出x(t)从高频到低频不同频段的分量；rn(t)表示信号x(t)的最终趋势。那么，EMD分解得到各IMF分量的过程如图10所示。

因此，任何一个信号x(t)都可以分解成n个本征模态函数和一个残余分量之和，各个本征模态函数IMF1，IMF2，…，IMF n分别表示信号x（t）从高频到低频的不同成分，每个频段所包含的的频率成分各不相同，残余分量r表示信号的平均趋势。

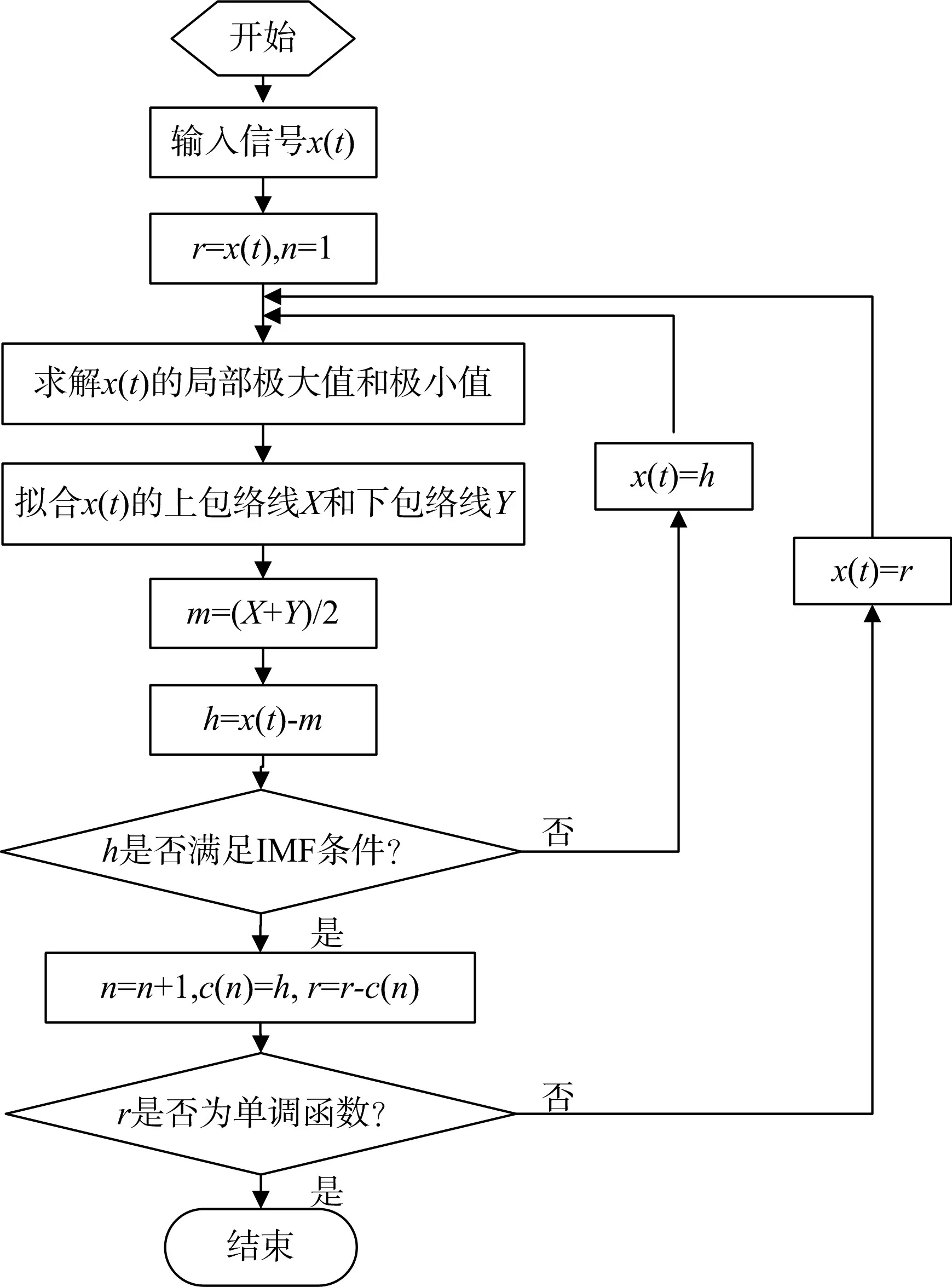
图10 EMD分解流程图

本文提取风电机组齿轮箱虚拟样机模型在正常、断齿、轴不对中状态下的振动信号，并用EMD方法对三种振动信号进行分解，得到了若干个平稳的本征模态分量IMF，各个IMF分量包含了不同的时间尺度信息，分别提取前8个IMF分量进行分析。如图11、图12、图13所示。

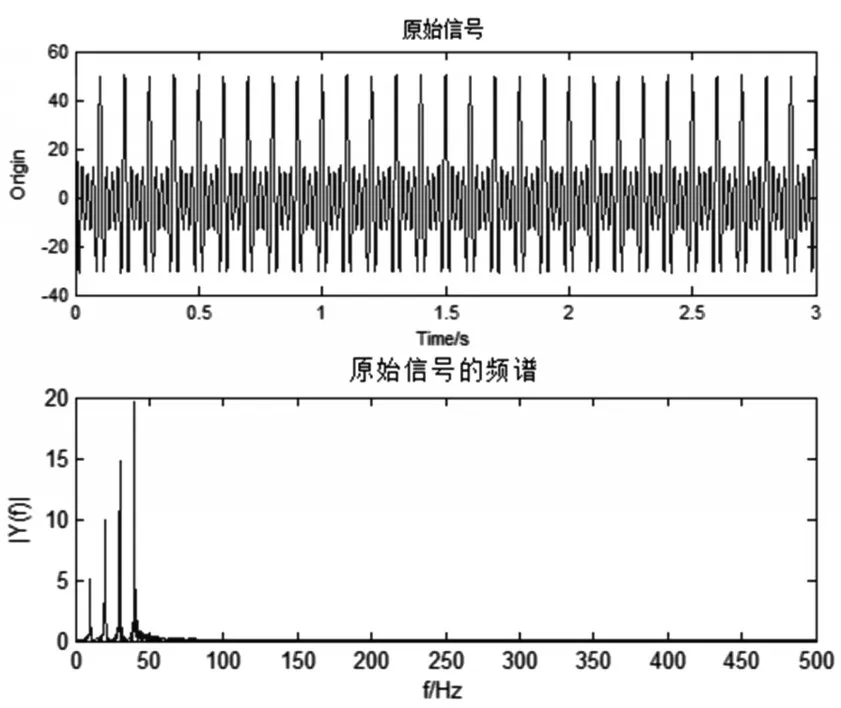
图11 齿轮箱正常信号EMD分解图

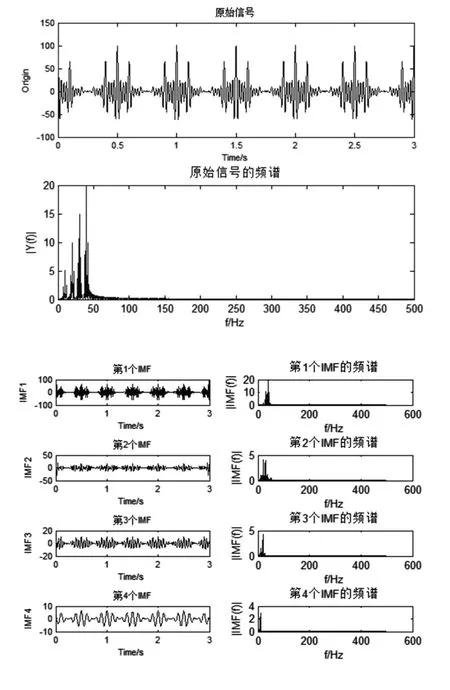
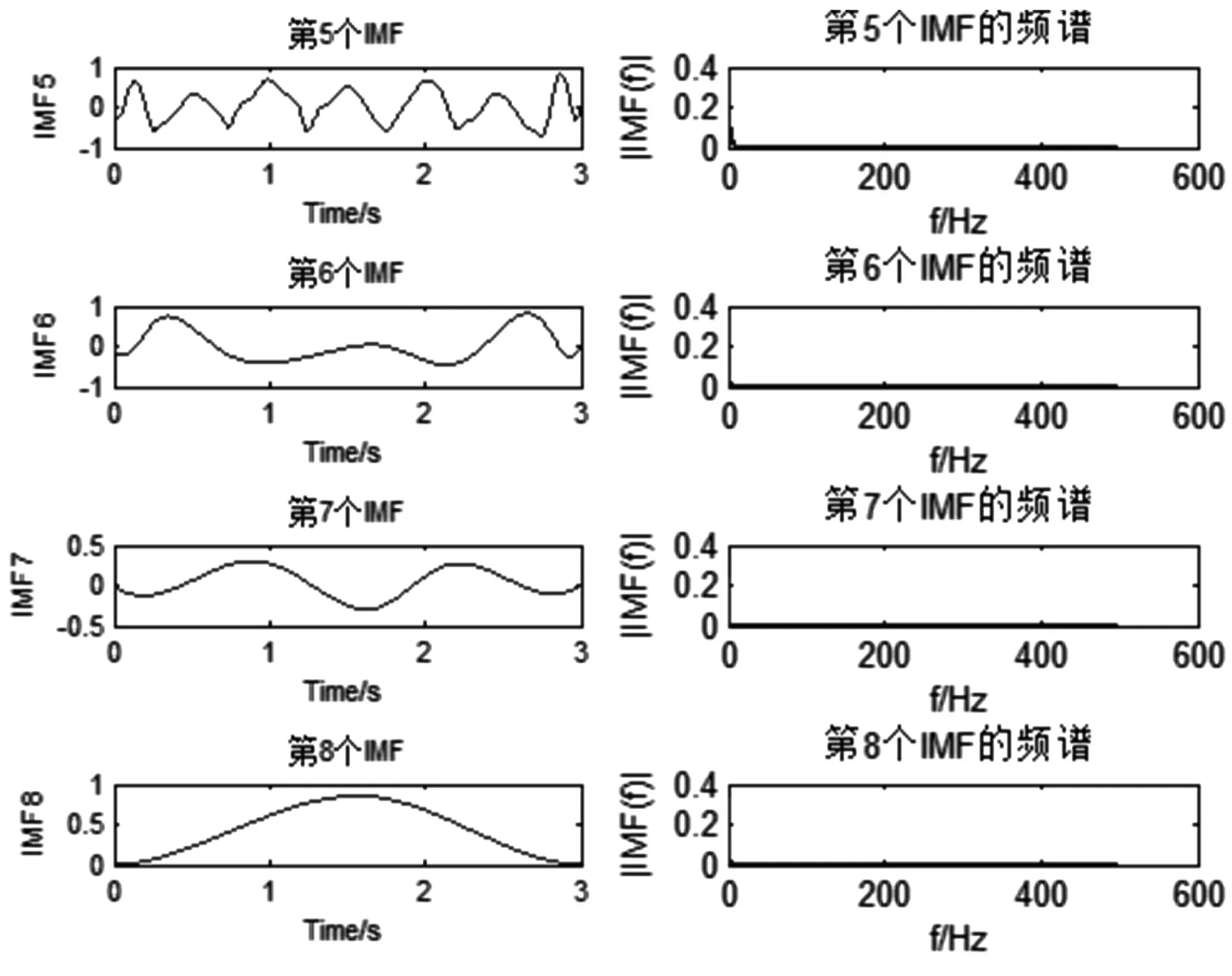
图12 齿轮箱断齿信号EMD分解图

图13 齿轮箱轴不对中信号EMD分解图

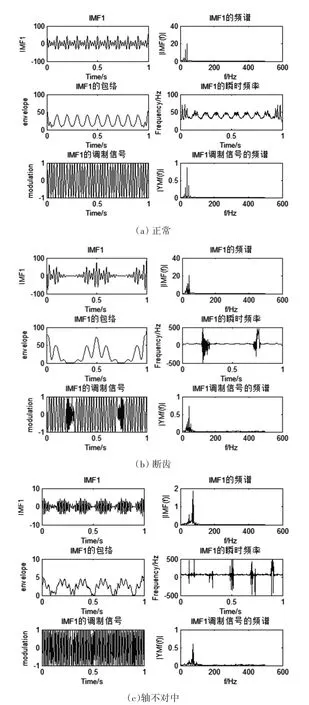
图14 三种状态下IMF1的Hilbert变换

通过与正常齿轮箱振动信号的比较可以看出，齿轮箱发生故障时振动信号出现高频突变，EMD方法将第1个IMF分量作为故障突变分解出来。为了突显故障引起的周期性冲击成分，对齿轮箱在正常、断齿、轴不对中三种状态下分解得到的IMF1分量进行Hilbert变换。经Hilbert变换后，故障造成的幅值变化引起信号包络的改变，使信号包络包含故障信息，因此通过幅值包络就能够反映故障状态。如图14所示，三种信号波形及其幅值包络差异明显：1）正常的齿轮箱，IMF1的包络图呈现周期性变化，幅值包络大小均匀，无任何突变现象；2）故障的齿轮箱，IMF1的包络图分别出现各种周期性突变的现象，故障特征明显。

5 结语

由于风力发电机组工作环境恶劣、工况复杂，风机齿轮箱振动信号受噪声干扰，难以判断真实有效的故障特征信号，因此，提出一种基于Adams建模的风电机组齿轮箱故障特征提取法。该方法在Adams中建立了风电机组齿轮箱的虚拟样机模型，首先通过给一恒定转速分析输入输出轴角速度曲线验证了模型的正确性，然后建立断齿、轴不对中状态下的齿轮箱模型。最后通过EMD方法分解振动信号得到包含不同故障频率信息的IMF分量，通过Hilbert变换使正常状态与故障状态的区分更加明显，实现了齿轮箱的故障特征提取，为风电机组齿轮箱故障诊断提供可靠依据。