最大最小偏差的多属性群决策方法*

张晓慧 冯 源 曹月静

（太原师范学院数学系 晋中 030619）

1 引言

多属性群决策理论是研究关于离散的有限个方案的决策问题，是系统科学、经济、管理社会学等领域研究的热点问题，其目标是对方案进行排序，并最终根据序关系选择最优方案［1］。文献［2］中提到，其中si表示第i个方案的综合评价值，wk表示第k个专家的权重，uj表示方案的第 j个属性权重，ri(jk)是第k个专家给出的客观测评值。最优方案的选择取决于综合评价值的大小，而综合评价值的计算必须确定专家权重与属性权重。

利用优化的方法确定专家权重与属性权重日益广泛，不少文献中提出的最小偏差法［3］、基于离差最大化方法［4］、基于方差最大化方法［5～6］、基于最小最大偏差的方法［7］等。结合OWA算子通过建立数学规划模型的优化方法也是决策问题的一个研究分支。有序加权平均算子（OWA）最早由Yager［8］在1988年提出的，经过多位学者的后续研究，相继提出有序加权几何平均算子（OWG）［9］、有序加权调和平均算子（OWHA）［10］、广义有序加权平均算子（GOWA）［10］等。结合（OWA）算子计算权重的优化方法如最小最大不一致方法［11］，Gholam R.Amin等在2006年的拓展的最小最大不一致方法［12］，拓展的为获取OWA算子权重向量提出的两种新方法［13］，AlimEmrouzejad等在2010年提出改进的最小最大不一小最大不一致方法［14］。

然而，上述所提几种利用OWA算子求解权重向量的方法并不是基于客观决策数据如文献［11～13］，而是只与位置有关的一种求解方法；文献［4～7］中基于离差和方差的优化方法在计算方案综合评价值时没有用到OWA算子。因此在本文中，提出了一种通过建立数学规划模型并结合OWA算子的新方法，对于属性权重完全未知的情形，给出一种基于决策数据本身，利用最小偏差最大化的思想建立目标规划模型，该模型能更大程度上反映客观决策结果，并实现多属性群组决策问题的排序。

2 基于离差最大化的几个模型

王应明1998年在文献［4］中提出利用离差最大化的方法来确定属性权重：

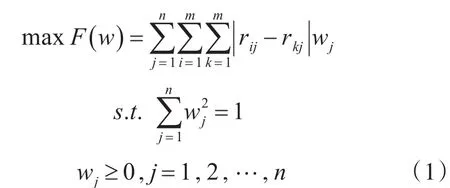
其中，wj表示属性权重，目标函数表示对于全部的n个属性，所有决策方案与其他决策方案的总离差达到最大。

基于上述模型，针对属性权重部分已知的多属性决策问题，徐泽水2001年在文献［5］中提出了一种方差最大化方法：

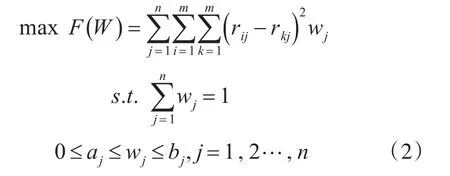
上述目标函数表示所有m个决策方案与其他决策方案对于全部属性的总方差达到最大。

万树平2009年在文献［7］中提出的基于最小最大偏差的属性权重确定优化模型：

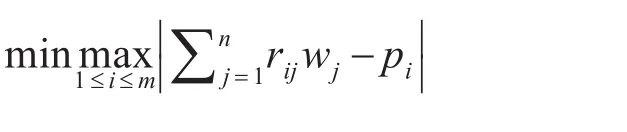
3 基于最大最小偏差的多属性群决策方法

3.1 问题描述

表1 方案决策信息

3.2 理论基础

在某个属性下若各备选方案的偏好信息越接近，则该属性对各备选方案的决策和排序引起的差异越小，所以该属性应被赋予较小的权重。Zeleny曾在文章［15］中提出：如果所有备选方案在同一个属性下具有相同的属性值，则大多数决策者认为该属性对方案的决策和排序没有影响。相反，如果各方案在某个属性下的属性值差异比较显著，那么该属性应被赋予更大的权重，这是因为该属性对备选方案的决策和排序具有更大的影响。因此，所求最优权重应使得所有属性值的差异最大化，若在同一个属性下，将第 i个方案 (i=1，2，…，m-1)与第 l个方案(l=i+1，…，m)属性值的最小差异最大化，则对于全部的n个属性，本文构造了一个目标函数，利用同一属性下两个不同方案之间的属性值最小偏差最大化的思想建立数学规划模型，则此时得到的最优权重是对方案排序作用最明显的。

且仅依据决策数据本身的差异性来反映权重，没有过多的对数据进行变换，保留了数据的原始信息。

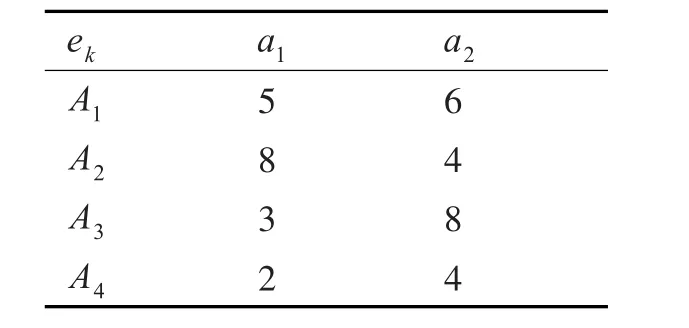
举例：以下述决策信息表为例，用模型（7）解属性a1与a2的权重。

模型如下：

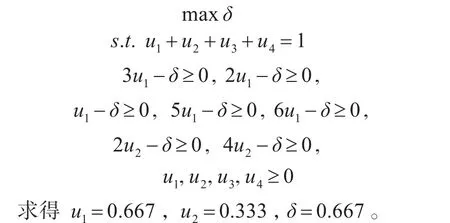
ekA1A2 A3 A4 a15832 a26484

求解模型（7）得到最大最小偏差方法的最优权重向量，该模型能够提供一个统一的权重向量，减少不合理的集结结果对决策结果准确性的影响，该模型简单且用lingo软件易于求解。

3.3 基于最大最小偏差的多属性群决策步骤

步骤一：标准化决策矩阵。为了消除不同物理量纲对决策过程的影响，有必要对不同量纲的决策矩阵进行规范化，规范化后的决策矩阵表示为，其中，k=1，2，…，t。属性类型一般可分为效益型、成本型、固定型等，效益型是指属性值越大越优的属性；成本型是指属性值越小越优的属性，固定型指属性值越接近某个固定值αj越优的属性。

其中，对于效益型属性：

由于每个专家自身的认知、经验不同，因而导致对属性的赋权也不同，因此有必要计算每个专家对各个属性赋予的权重值。

步骤四：由于b~ij表示第 j位专家对第i个方案的综合评价值，然而对于专家 j而言，若各个备选方案评判值差异越小，则该专家对方案的决策和排序所起的作用比较小，应给该专家赋予较小的权重。所以，最优专家权重的选取应使各方案间差异最大。因此，将模型（7）应用于综合决策矩阵B来确定决策者最优权重W=(w1，w2，…，wt)T，满足

步骤六：根据综合评价值s~i的大小进行降序排列，以s~i越大则方案越优为原则，对方案xi进行排序并选择最优方案，其中i=1，2，…，m。

需要注意的是，若专家决策信息表中，同一列有相同的属性值，则认为这样的属性值在方案排序时没有起到作用，在求解过程中对权重的贡献为0，因此，在计算过程中将其去除，忽略不计，转而求解在同一列中有差异的属性值。

这里所提出的基于最大最小偏差的决策方法是结合OWA算子来计算方案综合排序，并且同时可以得到最优属性权重向量与最优专家权重向量。

4 实例分析

以研究生论文答辩等级排序的多属性群决策问题为例。对四位研究生记为xi(i =1，2，3，4 )，作为决策问题的四个备选方案，考虑他们以下几个方面：a1为学术水平与实际能力；a2为论文撰写质量；a3为综合应用基础理论能力；a4为内容陈述及回答问题情况，这四项指标作为决策问题的四个属性，五位评审老师分别为专家 e1，e2，e3，e4，e5就上述 四 个 指 标 aj( j -1，2，3，4 ) 对 四 位 学 生xi(i =1，2，3，4 )给出评价结果，他们的偏好信息通过百分制系统来反映，见表2～6。

下述应用本文所提方法对备选方案排序并择优，具体步骤如下。

步骤1由于决策者偏好信息是由百分制系统来反映，量纲统一，所以不需要对决策矩阵进行标准化，所以

步骤2通过模型（7）计算5位决策者提供的决策矩阵中的属性权重向量，以第一个决策者矩阵为例，模型（7）可以重新写为

则模型（7）的最优解为

u1=0.333，u2=0.167，u3=0.333，u4=0.167，δ=0.333（保留小数后三位所得），则第一个决策者最优属性权重向量如下：

分别对其他四位专家提供的矩阵应用模（7）则得到下述不同决策者最优属性权重向量：

由此得属性权重矩阵：

上述模型的最优解为w1=0.192，w2=0.145，w3=0.32，w4=0.229，w5=0.114，δ=0.032（保留小数后三位所得），因此，最优专家权重向量为

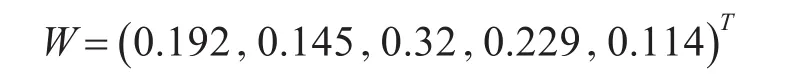
步骤5对综合决策矩阵应用OWA算子进行集结：

得到方案xi的综合评价值

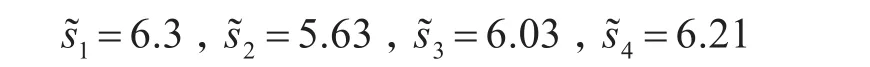
步骤6根据综合评价值s~i的大小比较，得到降序排列如下：

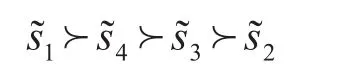
步骤7通过对s~i的排序获得方案xi的排序结果：

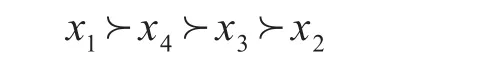
通过排序可以看出，最优学生是x1。

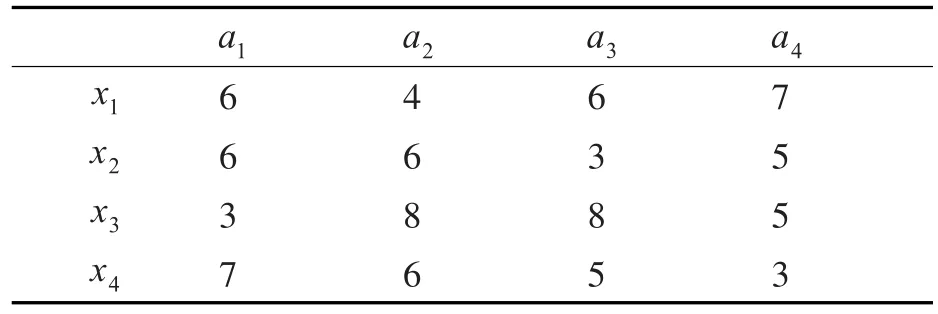
表2 决策信息(e1)

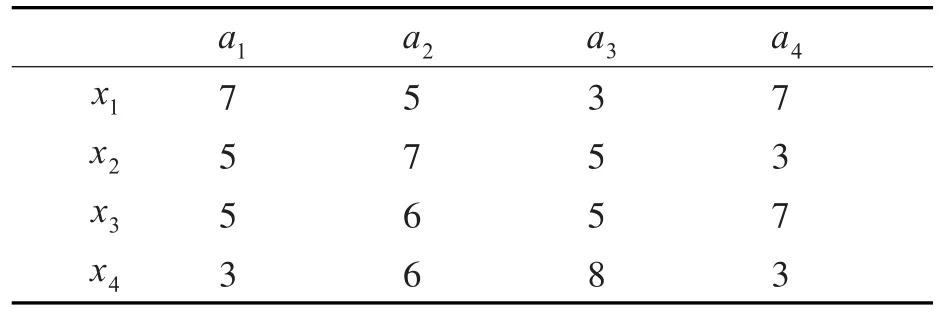
表3 决策信息(e2)

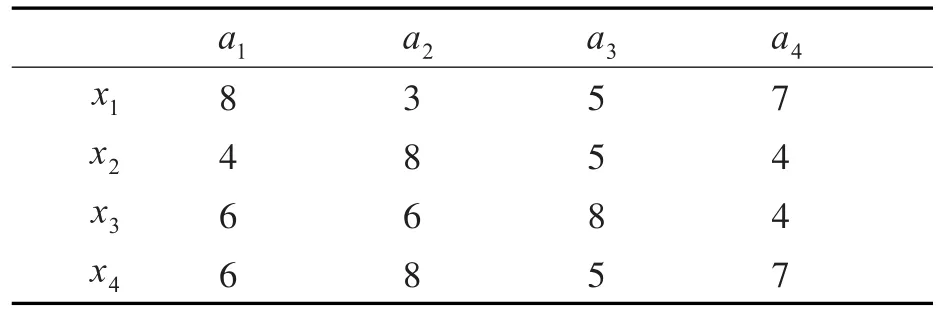
表4 决策信息(e3)

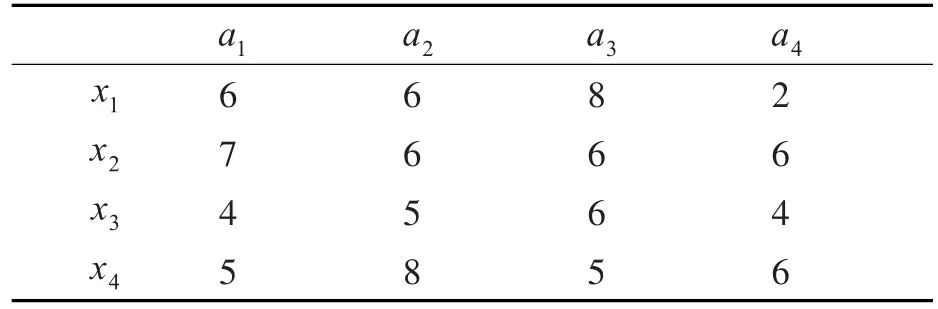
表5 决策信息(e4)

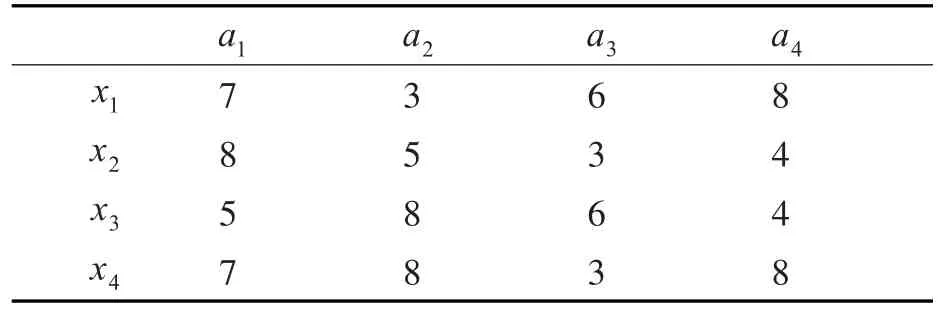
表6 决策信息(e5)

4.1 多种方法的比较研究

应用文献［16］中所提出的群组决策方法，经过计算得到的专家权重为 w1=0.215，w2=0.184，w3=0.206，w4=0.195，w5=0.2，结合文献给出的先验属性值30%，10%，30%，30%，应用加权平均公式计算方案的综合评价值，计算结果是s~1=6.013，s~2=5.012，s~3=5.466，s~4=5.589，因此方案排序结果是：x1≻x4≻x3≻x2。

经过比较发现，本文的方法与文献［16］所提方法排序结果是一致的。但是，文献［16］中的方法涉及到调整因子α的选取，而且属性的取值是用给定的先验值，若在无先验知识的情况下，则要对属性赋等权值，因而具有一定的主观性［17］。而本文所提的方法最大程度依据决策数据本身，通过决策数据间客观联系解决决策问题，是一种完全的客观赋权法，更能够反映客观实际。

另外，从方法的适用范围角度分析，文献［4～5，7］中所提及的多属性决策方法，仅适用于单一专家决策系统，对于群组决策问题并不适用。因为不同的决策信息表都会得到不同的方案排序情形，而文献中并没有给出如何将多个决策信息表中求解的信息进行综合。因此，本文的多属性群决策方法是对文献［4～5，7，16］的改进。

4.2 模型风险性的评估

对文中建立的模型做进一步评估。根据客观实际，考虑专家权重未知的情形，假设上述实例中，实际的t位专家的权重分别为(i =1，…，5) ，wi是应用本文的模型所得专家权重(i =1，…，5) ，因此，利用最大熵原理，用最大熵作为目标函数，为约束条件构造非线性规划模型，α为一个非负数，且不超过，因为现实情形中每一位专家理想的状态下都应被赋予权重。因此，构造的模型如下：

5 结语

本文提出的基于最大最小偏差的多属性群组决策方法不仅是对文献［4～5，7，16］的改进，同时还具有如下特点：1）充分利用客观信息，无论对于专家赋权还是属性赋权，都是从决策数据本身出发，避免了主观因素对决策结果造成的风险；2）最大化最小偏差的数学优化模型，不仅求解较为容易，而且能够求得最优专家权重与最优属性权重；3）结合OWA算子计算方案综合评价值并排序区别于已有的参考文献；4）尽管研究的是方案偏好信息为实数的情形，但是该方法可以进一步拓展到区间型、模糊型、语言型等领域。这将会在后续研究中进一步探讨。