含能材料热分解动力学求解及热安全性理论评估的进展

李 陈，马凤国，睢贺良，于 谦，银 颖，孙 杰

（1.中国工程物理研究院化工材料研究所，四川 绵阳621999；2.青岛科技大学橡塑材料与工程教育部重点实验室，山东 青岛266042）

1 引言

对含能材料进行热安全评价可以在制备、运输和储存过程中制定相应的安全措施，从而减小热爆炸造成的人员、经济损失［1-3］。热安全性评价的目标在于确定热失控的临界条件以及发生热失控前所经历的时间，通过热爆炸实验法（如联合国推荐的H1 方法）获得热安全性参数的可靠性高，但耗费的时间和经济成本高，所需样品量大，同时，热爆炸实验结果只适用于对特定样品（特定包装及尺寸）在某种特定温度条件下的安全性评价，难以满足复杂环境、多种温度下含能材料的热风险评估需求［4-6］。因此，近年大多采用热分解动力学的理论评估方法对含能材料的热安全性进行评价，并获得了快速发展和应用［7-13］。尽管该方法仍需要通过开展部分实验以求解动力学参数，但相对于传统热失控实验，其所需样品量大大减少（毫克量级），实验周期也大为缩减。此外，热分解动力学模拟方法的最大优势在于，一旦建立起准确的动力学参数或模型，结合体系热力学状态方程，就可以对多种温度条件下的热风险性进行评估。因此，理论模拟方法受到了研究和工程领域研究者的高度关注，目前已发展成为传统实验方法的重要补充。同时，对于一些处于实验室阶段的新型含能材料，由于受样品量限制而无法开展大批量的热失控实验，因此理论模拟方法被认为是唯一可应用的手段。

在目前国内外相关研究成果基础上，首先综述了获得热分解动力学参数的主要方法，通过分析简单线性拟合方法存在的局限性，进而探讨了近年来在专业研究热分解动力学领域内逐渐发展的两类重要方案：无模型等转化率法和基于动力学模型的模型拟合法，重点分析了模型拟合法的建模过程及其特点。在此基础上，结合热安全评估中的重要安全性参数，详细分析了基于热分解动力学对含能材料热安全进行评价的实际应用，最后对该方法目前仍存在的争议性问题进行了讨论，并提出在未来的相关研究中应充分重视样品状态⁃实验技术⁃评价目标之间的匹配性问题。

2 热分解动力学参数求解的理论方法

2.1 简单线性拟合法确定动力学参数

基于动力学模型的理论模拟方法，对含能材料热安全性进行准确预测的关键在于热分解动力学参数的正确性和体系热力学状态的精确描述。其中，准确的动力学参数是建立合理的动力学模型的基础，因此，求解热分解动力学参数是开展理论评估的首要任务。一般地，热分解动力学模型可由公式（1）确定［14］。

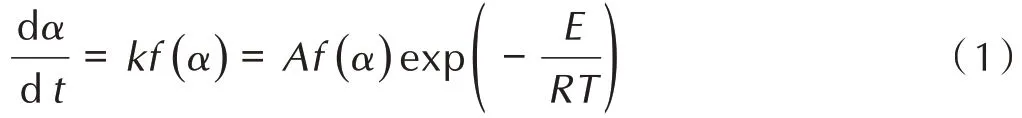
式中，α为含能材料在热分解过程中的转化率，%；t为时间，s；k为反应速率常数，s-1；T为温度，K；A为指前因 子，s-1；E为 活 化 能，kJ·mol-1；R为 气 体 常 数，8.314 J·（mol·K）-1；f（α）为反应机理函数。因此，反应速率可视为T和α的函数。

根据是否考虑反应机理函数f（α）的具体形式，热动力学参数的求解方法又可分为无模型法和基于反应模型的方法。其中，无模型法是一种无需假设机理函数就能获得动力学参数的方法，避免了对机理函数f（α）具体形式的确定，目前常见的无模型方法包括Flynn⁃Wall⁃Ozawa 积分法、Kissinger法、等温诱导阶段法和等转化率法等。其中，前三种方法均属于简单线性拟合法，基于DSC 曲线的一些特征点，通过特定方程的线性关系获得动力学参数，以下将结合一些研究实例，对简单线性拟合求解动力学参数的方法进行具体介绍。

2.1.1 Flynn⁃Wall⁃Ozawa 积分法

Flynn⁃Wall⁃Ozawa 法（Ozawa 法）的 基 本 思 路是，在不同升温速率下测试转化率α与温度T的关系，通过Doyle 近似式，推导出等式（2）［15］：

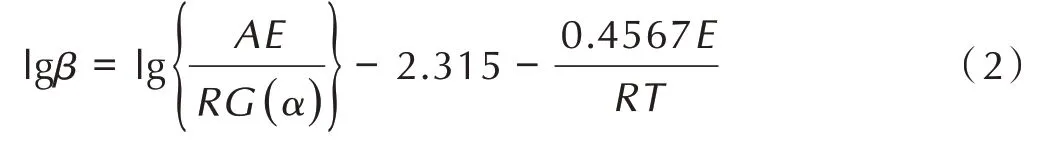
式中，β为升温速率，K·min-1；G（α）是f（α）的积分形式，在一定转化率α下，由于不同升温速率β下的各热谱峰顶温度处的转化率值近似相等，因此可用方程（2）中lgβ⁃1/T的线性关系来确定E。

在该方法的实际应用上，Zhu 等［16］根据三个升温速率下非等温DSC 曲线的特征峰值，用Ozawa 法计算了N，Nʹ⁃二硝基⁃4，4⁃偶氮⁃双1，2，4⁃三唑酮（DNZTO）活化能为（148±0.6）kJ·mol-1（图1）。类似地，Sivapir⁃akasam 等［17］对混合物（KClO3、K2Cr2O7、P、S）在四个升温速率下的非等温DSC 峰值温度进行处理，基于Ozawa 法得到E=129.167 kJ·mol⁃1。

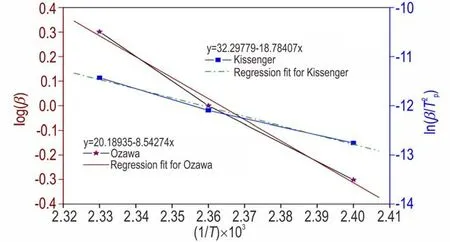
图1 Ozawa 法和Kissinger 法的线性拟合［16］Fig.1 Ozawa and Kissinger kinetic plots［16］

2.1.2 Kissinger 法

Kissinger 法是基于不同升温速率下的温度与峰值的关系，建立了峰温和升温速率的关系。Kissinger法认为f（α）=（1-α）n，经过数学推导得出Kissinger方程（3）［18］：

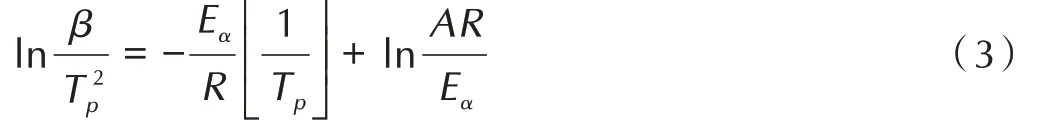
式中，β为升温 速率，K·min-1；Tp代表峰值温度，K；Eα代 表 活 化 能，kJ·mol-1。针 对DNZTO，Zhu 等［16］用Kissinger 法处理其热分解DSC 峰值温度与β之间的关系，获 得 其 活 化 能 为（148±0.2）kJ·mol-1（图1），与2.1.1 中的Ozawa 法获得的活化能基本一致。该方法除了用于DSC 数据分析，同样适用于热失重（TG）曲 线 的 数 据 分 析。 Li 等［19］用Kissinger 法 对3⁃氨基⁃4⁃偕氨肟基呋咱（AAOF）DTG 的峰值温度和升温速率进行了处理，得到其活化能和指前因子分别为108.82 kJ·mol-1和1010.35s-1。

2.1.3 等温诱导阶段法（Isothermal induction period）

等温诱导阶段法求解活化能的思路是基于等温DSC 的实验结果［20］，即通过实验测定不同温度（T）下达到最大速率的时间（诱导时间θ），利用lnθ-1/T的线性关系，根据等式lnθ=lnb+E/RT求得活化能E。路贵斌等［21］以β⁃亚硝基⁃α⁃萘酚为研究对象，基于等温诱导阶段法以1/T为横坐标，lnθ为纵坐标，借助线性回归对其热分解动力学参数进行了计算，得到其活化能为（105±7）kJ·mol-1。

总之，以上几种求解动力学参数的方法都属于简单线性拟合方法，其操作简单，能较方便地获得表观活化能，所以目前在热分析各领域的应用最为广泛。但是，上述几种简单线性拟合求解动力学的方法实际上存在许多局限性。首先，在推导过程中存在许多假定，如n级反应假定和单步反应假定等，对于存在自催化特征和复杂的多步反应而言，上述假定是不适用的，因此无法准确求解动力学参数。此外，从这些公式本身可以看出，由于对纵坐标原始数据进行了对数转换，原始数据中较大的偏差在对数坐标下可被大大缩小。因此，尽管在数学公式上进行对数转换是成立的，但如果考虑数值上的误差分布，则对数处理容易带来较大的偏差，导致尽管在对数坐标下的误差值低，但在原始坐标下的误差也可能较高。此外，这些简单的线性拟合方法仅通过选择反应的某些特征点（如DSC 放热峰值）进行线性拟合，而不是对反应全过程（DSC、TG 等曲线）进行优化拟合，这种处理也可能引入计算误差。

因此，由于简单线性拟合方法存在上述一系列的局限性，近年来在国际专业研究热分解动力学领域逐渐发展出无模型的等转化率法和基于动力学模型的模型拟合法两种方案，以克服简单线性拟合方法的内在缺陷。基于这两种方法能够对常见的量热数据曲线（如等温与非等温DSC、绝热量热ARC、微热量热等）进行整体拟合，即实现对物质热分解全过程的拟合优化，较之简单线性拟合方法可信度更高，并能够对复杂多步以及具有自催化特征的反应进行动力学参数求解，提高了其适用性。此外，上述两种方法可对不同量热模式下的数据进行同步拟合，可进一步提高其动力学参数的可靠性。下面将分别介绍这两种方法求解动力学参数的具体过程与实际应用。

2.2 等转化率法

等转换率法是一种无需假设机理函数就能获得动力学参数的无模型方法，在相同的转化率下，反应速率仅仅是温度函数的假定。等转换率法中最典型的为Friedman 法（也称为Friedman 方程），是Friedman 基于阿伦尼乌斯等式变形，提出的一种固态物质分解动力学等式，具体形式见等式（4）［22］：

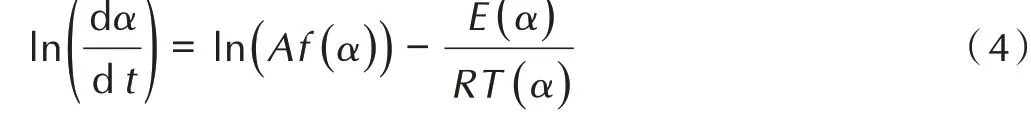
从公式（4）中可以看出，若假设在任意特定的转化率α下f（α）为定值，则ln（dα/dt）与1/T存在线性关系。因此，可通过直线ln（dα/dt）⁃1/T的斜率和截距分别求得活化能E和指前因子A。可见，对于每一个特定的转化率α，均有一个对应的活化能E。若令转化率α的间距取得足够小，则可以获得一系列α与E的变化趋势，从而可获得E随α变化的关系曲线。因此，等转化率法的实质是建立Eα⁃α的变化关系，由一系列特定转化率下的动力学方程对反应全过程进行描述，从而避免了简单线性拟合仅用一个活化能描述整个反应的弊端。

基于Friedman 法获得的动力学参数，可进一步对反应进程进行判断。根据热分析动力委员会的建议［22］，利用Friedman 法所求出的活化能E随α的变化关系，可以初步判断机理模型是否为单步反应。例如，陈网桦等［23］基于动态DSC 分析和Friedman 方法，得到了苯甲醛肟（BO）的活化能E随着转化率α变化的趋势（图2a）。他们发现在转化率0.1～0.9 范围内，E随α的增加明显降低，意味着BO 的分解过程不能用单步反应进行描述，而应为复杂的多步反应。而Liu 等［24］通过Friedman 法研究了偶戊二异丁腈（AMBN）分解过程的热动力学参数，发现活化能在较大的转化率范围内保持恒定（图2b），这表明AMBN 的分解是一个简单的单步反应。通过等转化率法获得的活化能变化趋势，能初步对反应的复杂性进行判断，对于简单反应而言，能较为容易地获取动力学参数，对于复杂的反应，则需要进一步考虑到机理函数进行动力学参数的判断。

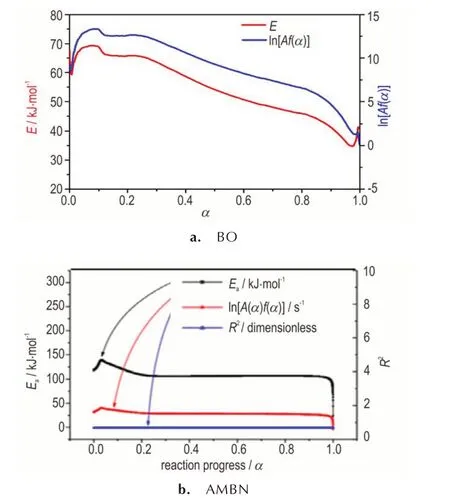
图2 基于等转化率法求解的动力学参数（E 以及ln（Af（α）））与转化率α 的关系［24］Fig. 2 Relationship between kinetic parameters （E and ln（Af（α））and conversion rate α based on isoconversional method for BO［23］and AMBN［24］

综上，等转化率法不需要有关反应机理函数f（α）的任何信息，避免了由于反应机理函数错误的选择而导致不正确的动力学参数求解。但相应地，等转化率法没有给出有关反应机理，特别是多步反应机理的任何信息，同时无法区别自催化和非自催化反应，而这将直接影响动力学参数的可靠性。同时，需要指出的是，等转化率法的基本假定并不是公理，原则上仅适用于简单的没有明显步骤重叠的连串或独立反应，而在某些情况下，该基本假定可能并不适用。例如，对于存在平行反应的复杂热分解过程，在相同转化率下，不同升温速率下不同分支路径的占比可能是不一样的，因此通过等转化率法计算的活化能是不准确的；而对于存在明显重叠的连串反应，在重叠区内由于等转化率法获得的活化能概念模糊，分析结果不可靠；此外，对于吸放热耦合的反应过程，等转化率法可能会出现负的转化率导致无法计算动力学参数。因此，在这些情况下，基于等转化率法求解动力学存在着明显的困难和局限性［25-29］。

2.3 基于反应机理函数的动力学参数求解方法（模型拟合法）

2.3.1 模型适配法

针对反应机理函数的确定，需要特别指出的是，胡荣祖［30］先生在其《热分析动力学》一书中曾详细介绍了几种常用的最概然机理函数推断法，其基本思想是从41 种固定机理函数中，选择较合理的具体机理函数形式。目前，国内大量文献广泛使用模型适配法进行反应机理函数的推断［31-35］，即：先通过无模型的Kiss⁃inger 或者Ozawa 法方程获得初始活化能，再将41 种热分解机理函数分别代入到常见的热分解动力学分析方程中（表1），利用这些公式对峰值温度和G（α）机理函数的关系进行线性回归处理获得一系列活化能，将所得结果与初始的Kissinger 法和Ozawa 法获得的活化能进行比较，找出活化能最为接近时所对应的机理函数，从而推断出该反应的反应机理函数。这一方法的具体应用本文不再举例赘述。总体而言，该方法较之简单线性方法具有明确的机理函数，在一些情况下可以更好地描述热分解反应。但是这种方法仍存在较大的局限性，首先，其机理函数推导过程存在大量的简化，在实际使用过程中，当热分解反应过程较复杂时，这种模型适配的目的就很难达到，例如涉及连串反应、平行反应、熔融分解反应以及这些反应的组合，实际上无法基于41 种反应机理函数的任何一种来进行适配，从而很难准确判断出机理函数。此外，模型适配法的基本运用过程是采用单一升温速率下转化率与温度的对应关系，而不是通过同一个动力学模型对不同升温速率的曲线进行同步拟合。

表1 动力学分析方程Table 1 Kinetic analysis equations

因此，本文将重点讨论模型拟合法（model⁃based simulation approach）求解动力学参数的方法，其基本思路是：首先选择合适的反应机理函数f（α），确定反应动力学方程，再利用非线性优化对不同实验数据进行同步拟合，从而得到动力学参数。这一方法的特点在于：（1）需要确定反应机理的基本类型，如是N 级反应还是自催化反应，是单步反应还是多步反应等，对于某些材料体系，其分解反应可能是几种反应过程的组合；（2）通过对样品反应全过程的非线性优化拟合，可以对反应特别是复杂反应的过程进行更为精确的描述，从而提高动力学参数的准确性；（3）该方法能适用于更加复杂的反应机理，并且能同时对多个升温速率和多种热分析模式下的数据进行同步处理。

2.3.2 N 级反应与自催化反应的判定

一个合理模型的建立首先需要考虑到反应过程的特点.从化学反应的角度，可以将材料热分解的反应类型分为N 级反应（N⁃th order）和自催化反应（auto⁃catalytic reaction）。其中，N 级反应模型（A→B）是一种典型的减速型模型［36］，其反应速率方程可表达为：

式中，k是速率常数，s-1；n是反应级数；（1⁃α）n是机理函数f（α）的表达式。

与N 级反应不同的是，自催化反应模型［37］是在反应初期速率较慢，随着反应的进行，其分解产物可以作为催化剂参与分解反应，从而使得反应速率不断加速，体现出一定诱导期后达到最大值，之后因反应物的不断消耗又逐渐下降的一种反应过程。基于这一过程，其反应速率可表示为转化率的函数：式中，m，n为自催化模型的反应级数。值得注意的是，上述方程忽略了自催化反应的引发反应，对于强自催化反应而言，这种忽略对动力学求解影响不大，但对于弱自催化反应的情况，引发反应则不能被忽略。Benito⁃Perez 模型［38］（简称BP 模型）是将引发反应考虑在内的自催化模型，即包含两个步骤的自催化反应，该假设如下：

式中，k1和k2分别为两步的速率常数，n1和n2为自催化反应的级数。

当BP 模型中的反应级数都简化为1，BP 模型简化成为Kamal⁃Sourour 模型（简称KS 模型）［39］，得到另一个速率方程式（8）：

式中，参数Z（Z=k1（T）/k2（T））称为自催化因子，由于Z是两个速率常数的比值，且两个步骤的活化能并不相同，因此Z 是温度的指数函数。当Z=0 时，反应是单一的一级反应；随着Z增加，自催化特征变得越来越明显。该模型简单、通用，对于研究自催化反应的各种现象有很大帮助。

对于含能材料的热分解反应，其反应机理的选择直接决定进一步的动力学参数求解，因此反应机理的判断十分重要。判断反应为N 级或自催化反应的常用实验方法是等温法（包括等温条件下的DSC、微量热实验）［38，40-41］。等温量热实验的基本原理是：在物质热分解起始温度附近取某一温度点作为等温条件加载，由公式（5）和（6）易知，若在等温条件下物质的放热速率随着反应时间的增加而逐渐下降，且单位质量的放热量与动态非等温量热的基本相当，说明其分解遵循N 级反应；若物质的放热速率随时间的增加先逐渐增加至最大值，之后逐渐下降，即体现出放热速率与时间呈“钟形”曲线关系，则说明这种物质的分解机理为自催化反应（如图3）。需要指出的是，该方法需要选择合适的温度点作为等温条件，若温度选择过低，则诱导期会过长，可能得到不分解的错误结论；温度选择过高，则放热曲线不完整，容易造成误判。因此，等温DSC 实验温度的选择应该与动态DSC 的测试结果相结合，才能做出更准确的判断。

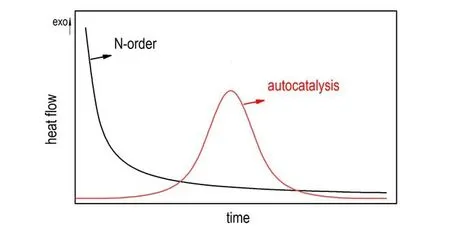
图3 具有N 级反应与自催化反应特性的等温DSC 放热速率曲线［38］Fig.3 Heat flow curves of isothermal DSC of reaction of N⁃order and autocatalysis［38］

2.3.3 复杂反应的动力学参数求解

在判定N 级或自催化反应机理的同时，一般还可以结合等转化率法的活化能变化趋势确定反应为单步或多步反应（见2.2 中讨论），研究表明，许多有机物质的热相关反应都是具有自催化特征的多步复杂反应，只有采用较复杂的多参数动力学模型和非线性优化才能对热分解全过程进行最佳拟合。对于复杂反应的动力学求解，目前主要以化工工艺中间体有机物的相关研究较多，而单纯针对含能材料的研究报道相对较少，但两者仅是对象不同，其基本的思路是相同的。因此，以下将结合中间体有机物的相关研究工作，对求解复杂反应的动力学参数及其模型的基本思路和方法进行介绍。

Kossoy［42］系 统 对 比 了 简 单 标 准 方 法（Standard method）和复杂专业方法（Expert method）对树脂固化反应的动力学评估（图4）。其中，简单标准方法是N级模型和Arrhenius 线性拟合的方法，而复杂专业法通过构建多反应路径动力学模型和非线性优化拟合，进而开展动力学参数的评估。结果表明，简单模型（N 级反应）的拟合曲线相对实验数据具有较大偏差，特别是在自加速速率的起始阶段存在较大的差异性，表现出的表观活化能更高，即在N 级反应的假设下，需要更高的温度去促进反应；而复杂专业法采用自催化模型对实验结果进行拟合，结果表明该模型的拟合系数较高，可对分解过程进行精确描述。这表明对于复杂反应，虽然动力学建模的过程相对困难，但是所构建的多路径反应模型能更加准确地对反应进行描述。

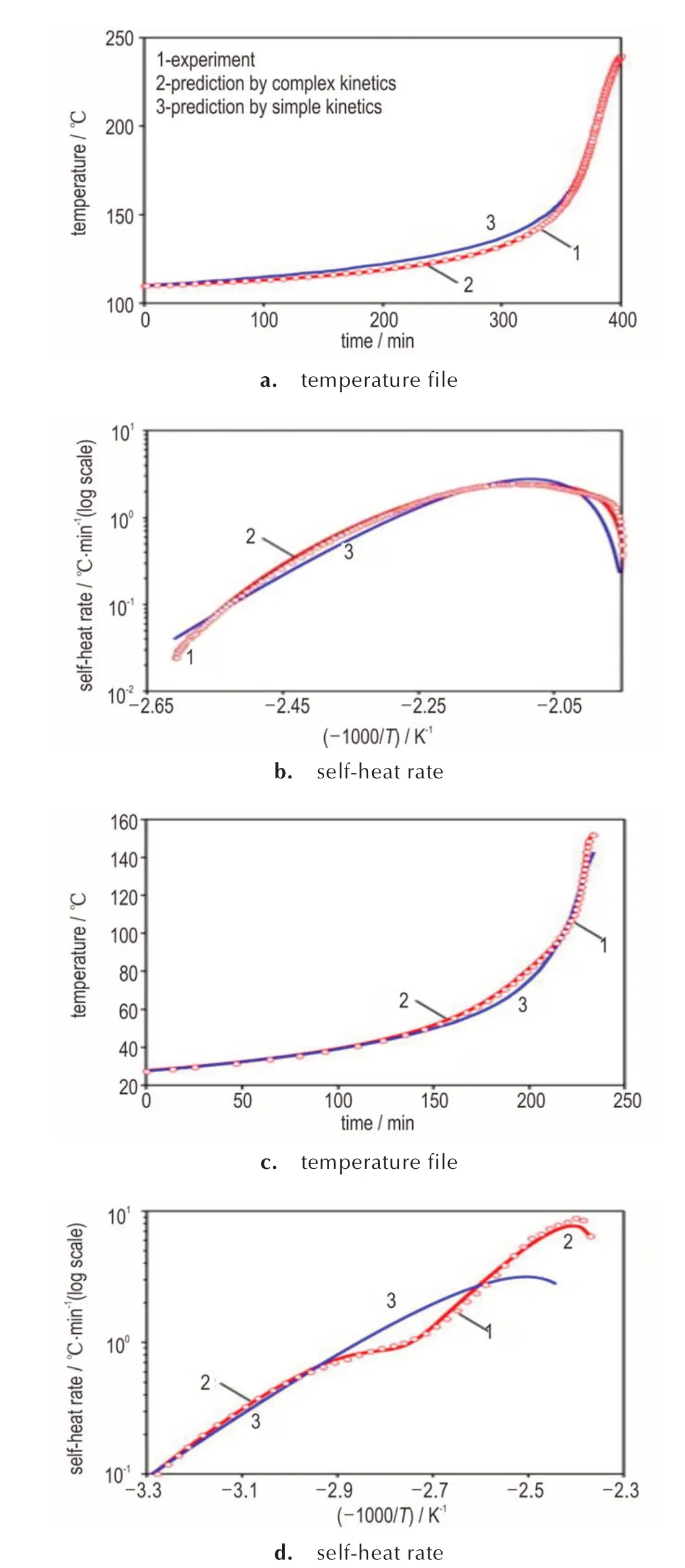
图4 树脂固化和酚醛反应的ARC 数据［42］Fig.4 ARC date on resin curing and phenol⁃formaldehyde re⁃action［42］

在此基础上，Kossoy 等［43］系统地讨论了建立动力学模型的步骤，并将动力学模型分为描述性模型和通用性模型。前者是指能详细的描述分子层次上的反应机理模型，但需要提供初始条件（比热容、组成、分子质量、密度等）；后者是假设反应程度是反应系统的固定变量，能提供一些总体上的信息，但不能构建详细的反应机理。作者对不同起始温度的酯化反应进行了自加热速率和分别基于两种模型在绝热条件下热产生速率的拟合，结果发现：描述性自催化模型恰当地拟合了酯化反应过程的自加速速率。另外，Kossoy 等［44］还对偶氮二异丁腈（AIBN）在熔点之下的固相分解动力学进行了分析，发现该过程包含了两步连续反应。其中，第一步包含两个连续的自催化反应，第二步为单步的N级反应，证明AIBN 的分解是一个较为复杂的过程，不能通过简单的N级反应进行描述。

由于AIBN 是一种重要的中间体有机物，且其热分解是一种典型的吸放热耦合过程，因此其热分解反应吸引了大量研究者对其开展进一步的深入研究。Moukhina 等［45］对动力学模型的建立做了更加细致的研究工作，他们分析对比了两种可能的分解模型，并同时对AIBN 在熔点之下的等温数据和不同升温速率下的非等温数据进行拟合。其中，模型一包含了熔融和液相分解两个步骤，表达为：

A⁃1→B⁃2→C

其中步骤1 为自催化反应；步骤2 为N级反应。在此基础上，进一步考虑到固相状态直接发生热分解的过程，对模型一进行调整得到模型二，表达为：

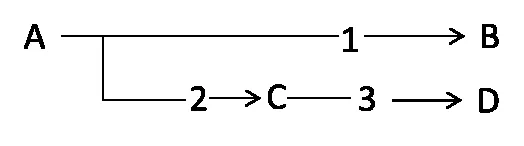
可以看到，模型二包含两个路径和三个步骤：步骤1 是固相的自催化分解反应，步骤2 是吸热熔融的自催化反应，步骤3 是放热分解的N级反应。结果表明，模型二可以更准确地描述AIBN 的热分解全过程。AIBN动力学模型的建立进一步揭示了其热分解反应是一个十分复杂的过程，用简化的单步模型或N级模型是无法得到准确的动力学参数的。

陈网桦等［23］研究了苯甲醛肟（BO）的分解反应，指出BO 分解包含两个平行反应（N级反应和自催化阶段）。表2 给出了BO 分解的动力学参数，对比2.2 节中图2a 中Friedman 法得出的活化能，可以发现：发现Friedman 法在低转化率下求得的活化能与E1接近。可见，等转化率法获得的活化能变化趋势可以作为模型拟合法中的活化能初值的参考，再进一步通过非线性优化拟合得出精确的动力学参数。本课题组曾以CL⁃20/HMX 共晶为一类结构较为特殊的含能材料，对其热分解行为进行了研究［46］，发现共晶的放热量与升温速率有明显的依赖关系，意味着其热分解至少存在两个平行反应，从而基于双平行自催化反应模型对其热分解反应过程实现了精确拟合，结果表明两个平行反应对总反应的贡献是随着升温速率变化而动态变化的。

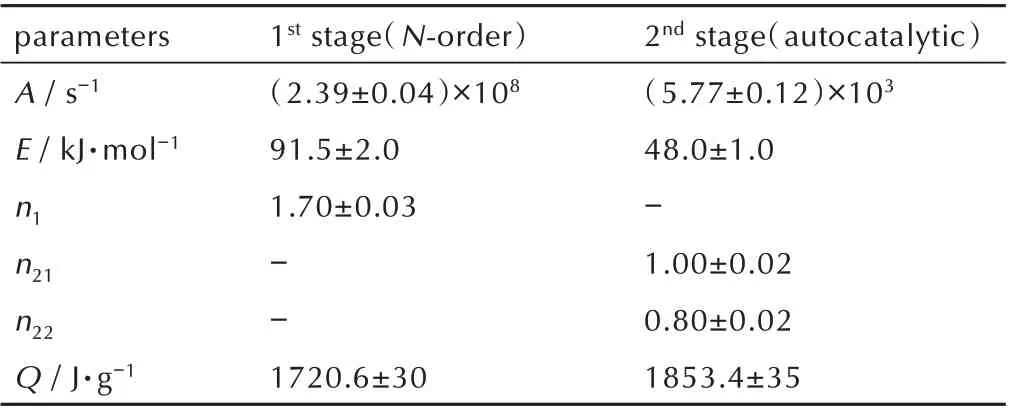
表2 BO 基于分解模型的动力学参数［23］Table 2 Kinetic parameters of the reaction model for BO［23］

此外，陈莹莹等［47］对硝基胍（NQ）溶液进行了动态和等温测试，基于Friedman 法得知动态模式下的活化能为84～78 kJ·mol-1，等温模式下的活化能为86～78 kJ·mol-1，且数值变动很小，表明其热解过程可用单步机理描述，进而采用包含引发反应的自催化模型能实现对等温和动态实验结果的精确拟合。Shu［48］针对过氧化异丙苯在异丙基苯中的溶解过程。采用两步自催化反应模型和多步平行反应模型对实验数据进行拟合，发现精细的多步平行反应模型能更好地模拟自催化分解反应。

上述研究工作均表明，有机化合物的放热反应过程，其内在的反应机理一般都是十分复杂的，通常是连续多步反应以及平行反应的组合，同时还可能伴随自催化的特征。在这种情况下，通过简单模型或对实验数据进行线性化处理，是难以对放热反应进行合理描述，也不能获得准确的动力学参数，而动力学参数的偏差可能将导致后续热安全性评估的严重失真。同样地，对于许多含能材料而言，其分解反应较为复杂，有必要通过建立结构相对复杂的动力学模型，对含能材料本身的热分解行为进行准确描述，从而获得正确的热分解动力学参数。

3 基于热分解动力学理论对热安全性评价

3.1 热安全性评估的理论基础

在建立合理的热分解动力学模型的基础上，结合体系⁃环境之间的热平衡状态方程，就可以进一步预测材料在多种温度条件下的热安全性参数。根据已报道的研究工作，除含能材料外，通过热分解动力学参数对热安全性评估的研究在一些涉及化工工艺过程的有机物中开展得较为深入，因此将其在热安全性评估中的具体应用一并进行介绍。

常用的重要热安全性参数包括［49-50］：

（1）自加速分解温度（self⁃accelerating decompo⁃sition temperature，SADT），常用定义为：7 天或7 天内从低于环境温度2 ℃升到高于环境6 ℃的最低环境温度；

（2）绝热诱导期（adiabatic time to maximum rate，TMRad），通常用绝热条件下反应体系达到最大反应速率所需要的时间来评估样品在不同温度下发生反应失控的可能性，它表示在绝热条件下达到最大反应速率所经历的时间；

在实际的计算过程中，基于上述方法获得的热分解动力学参数，利用有限元方法（Finite element anal⁃ysis，FEA）可对物质在不同环境下的热行为及热安全性进行模拟，该方法要求对临界设计参数进行初值定义，包括物质质量、包装形状、尺寸、绝缘层壁厚，同时需要确定物质与容器的比热容、导热系数、热交换系数等参量。通过这种方法，可以预测在不同温度情况物质热分解过程的热累积和反应进程，确定临界设计参数对贮存和运输安全性的影响。

物质热分解过程产生的热量将与周围环境发生热交换，因此体系中的温度分布与其产热速率、比热容、导热速率等密切相关，对于固体而言，我们常常忽略热对流作用的影响，根据傅里叶热传导定律（9）［51-52］，

式中，ρ为样品密度，g·cm-3；Cp为样品热容，J·g·K-1；T为样品温度，K；t为传热时间，s；λ为样品的热导率，W/（m·K）-1；ΔT为共晶样品放热段的总温升。W为热功率，可表达为（10），

式中，Qi为反应生成热，J·g-1；i为平行反应数量；Qi∞为样品升温过程中总的放热量。ri为反应速率，可表达为（11）：

式中，α为反应物的转化率，则dα/dt为转化速率，可通过2.2 与2.3 节中所介绍的理论方法，求解出热分解动力学参数带入上述方程（9）～（11）中进行表达。

此外，体系边界条件的定义也对热安全参数的评估产生重要的影响。边界条件常常通过牛顿换热方程来定义［3］：

式中，U是传热系数，W/m2·K；“wall”和“e”分别为与边界和环境相关的参数。结合方程（9）～（12），就可以模拟出含能材料在多种环境条件下的热安全性参数。

3.2 热分解动力学在热安全性评估中的具体应用

Lin 等［53］基于非等温DSC 对六硝基六氮杂异伍兹烷（HNIW）和奥克托今（HMX）建立了基于自催化反应机理的热分解动力学模型，并讨论了扫描速率对热安全参数的影响，推算出评估HNIW 和HMX 热爆炸的一些重要参数（表3）。

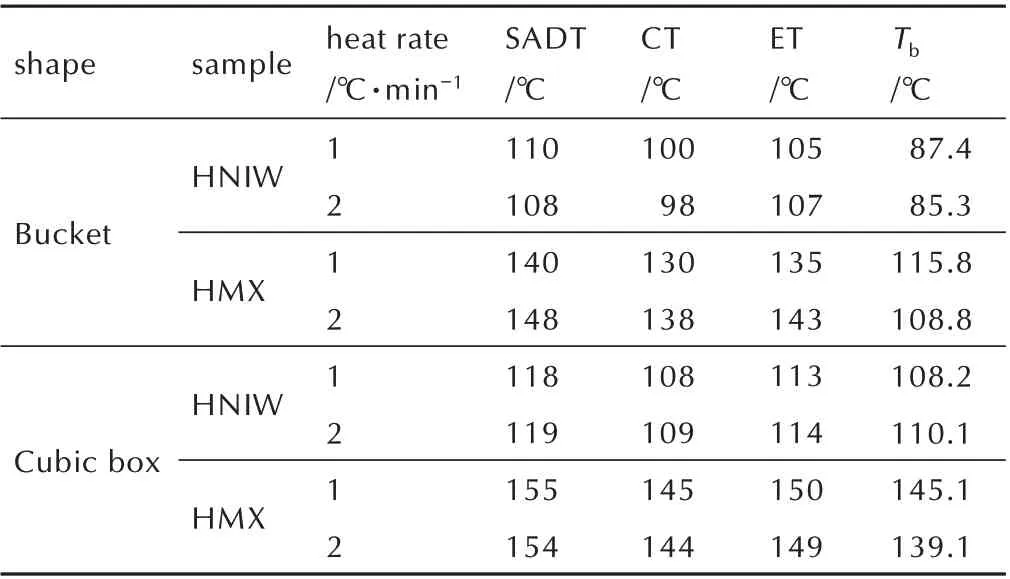
表3 HNIW 和HMX 热爆炸参数［53］Table 3 Thermal explosion parameters of HNIW and HMX［53］

本课题组也曾针对CL⁃20/HMX 共晶新型含能材料［46］，建立了两个复杂的平行全自催化反应模型准确描述其热分解行为，并结合有限元方法推算出50 kg包装下共晶的SADT 为138 ℃，24 h 绝热条件下达到最大温升速率的温度为151.64 ℃，这为CL⁃20/HMX共晶型含能材料的贮存和安全使用提供了参考。汪维俊等［54］基于动态DSC 数据对偶氮二异丁酸二甲酯（AIBME）的热分解过程建立了两步连串自催化模型，并得出其SADT 值为30 ℃，在常温下可分解，故应在储存和运输过程中加强温度的监控。在聚合物黏结炸药（PBX）炸药方面，Niu 等［55］基于等转化率法和有限元分析研究了TKX⁃50 和TKX⁃50 基PBX（PBX⁃T）的热安全性（图5），研究结果表明黏结剂的加入明显降低了TKX⁃50 的热稳定性，25 kg 木桶包装材料中的TKX⁃50和PBX⁃T 的SADT 分别为128.87 ℃和92.02 ℃。

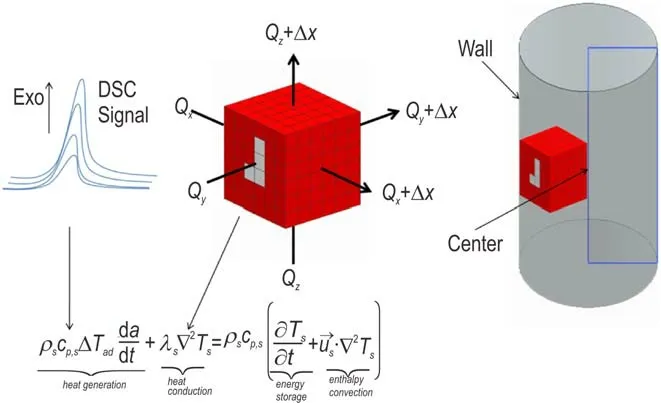
图5 在容器和体积元件上的广义热平衡［55］Fig.5 Generalized heat balance over a container and a volume element［55］

值得注意的是，对于某些具有熔融分解特性的材料而言，基于其熔融状态下（液相）热分解动力学参数预测其固相状态下的热安全性是不合适的，也需要十分注意样品状态⁃测试方法⁃研究目标之间相匹配的问题。以AIBN 为例，如前所述，AIBN 的热学行为是极为复杂的：随着温度的升高，AIBN 将经历晶型转变⁃固相分解⁃熔化⁃液相分解等一系列过程，其热流变化曲线如图6 所示。由图6 可以看到，在低温区域A，AIBN保持单一的固相状态；而当温度升高至B 温区时，样品经历了明显的晶型转变引起的吸热过程，并在更高的C温区内发生部分固相分解反应（放热）；在更高的D温度区间内，AIBN 发生显著的熔融吸热过程，并以液相状态发生热分解反应（温区E）。可见，由于AIBN 在不同温度区域体现出不同的热学行为特征，要实现对AIBN 的热安全性评价，必须遵守样品状态⁃测试方法⁃研究目标之间相匹配的原则。具体地，若研究目标为实现对AIBN 在相对低温下的固相状态的热安全性评价，则应采用等温量热测试方法，选择在A温度区域内的温度点下进行量热测试，以此为基础获得动力学参数及模型。

表4 总结了前期针对AIBN 热分解动力学研究的相关工作，其中，Malow 等［4］通过UN.H1 实验法测得AIBN 在50 kg 包装下的SADT 值为47 ℃。而Guo等［56］利用非等温DSC 实验手段，采用等转化率法在液相分解段中求解AIBN 的热分解动力学参数，并以此计算出AIBN 的理论SADT 高达63 ℃，与实验值47 ℃相比，明显偏高。产生这种显著偏差的原因在于，非等温DSC 测试获得的热分解特征实验值来自于熔融状态的AIBN，也即图6 中的E区，故其计算获得的动力学参数描述的实际上是液相状态AIBN 的热分解，因此，这一状态下的热动力学参数并不能准确评估固相状态下（图6 中A温区）的热安全性。针对这一问题，Kossoy 等［44］进一步提出通过等温量热法获得AIBN 的热分解动力学参数，基于AIBN 熔点之下进行等温DSC 实验（图6 中C温区），他们构建了一个包含两个平行反应路径的动力学模型，并据此模拟出20 kg 和50 kg 包 装AIBN 的SADT 分 别 为47.5 ℃和46 ℃。可见，理论计算值与实验结果比较接近，说明基于熔点之下的等温测试相比之下可靠性更高。类似地，Roudit 等［57］也开展了针对温度C 区间的等温量热实验，他们对比了KS 模型法和等转化率法对于SADT 的模拟计算值，两种方法计算出的SADT 值与实验值均很接近，在50 kg 包装下的SADT 模拟结果为47.16 ℃。Moukhina［45］认为建立的动力学模型应该能够同时对动态和等温的数据进行拟合，他们基于等温DSC 数据（图6 中C温区），建立同时考虑固相分解⁃熔融⁃液相分解的动力学模型，并计算出5，20，50 kg AIBN 的SADT 分别为51.9，48.4，46 ℃。在上述研究基础上，Roduit 等［58］进一步提出应将等温量热实验的考察温度降低至A温区，以避免AIBN 在温度B区间发生晶型转变的影响，他们利用灵敏度更高的微量热仪对AIBN 发生晶型转变之前设置了一系列等温点（55，60，65，70 ℃）进行实验，获得了更精确的AIBN低温相热分解特征数据，并据此求解了AIBN 低温相的热分解动力学参数，计算获得AIBN 的SADT 为46 ℃。可见，对于热分解存在吸放热耦合的含能物质，选择在其熔点之下，甚至晶型转变温度以下进行等温实验是更为合理的实验方法，由此计算出的SADT 值与实验结果能较好地吻合。而忽略熔化过程，直接通过液相状态下的动力学参数去评估低温固相下的热安全性是不准确的。

表4 AIBN 热分解相关工作Table 4 Previous work on thermal decomposition of AIBN

上述针对AIBN 的研究工作，发现对于存在吸放热耦合的熔融分解反应，必须特别注意样品状态⁃实验技术的匹配性问题。若研究目的为评估低温固相状态下样品的热安全性，则不应采用非等温量热实验以及高温液相状态样品的热分解动力学参数进行求解，而应在确保样品处于固相状态的相对低温区间，采用等温量热方法获得其热分解数据，并据此求解热动力学参数和热安全性理论评估。在今后的研究中，对于许多具有熔融分解特征的含能材料，包括六硝基茋（HNS）、硝基胍（NQ）、苯并三氧化呋咱（BTF）等，也应借鉴AIBN 热分解动力学的研究思路。

4 总结与展望

基于热分解动力学评价含能材料热安全性受到了相关领域的普遍重视。目前，包括含能材料在内的危险物质的热安全性评估已建立起了基本的方法和体系：首先建立合理的热分解动力学模型，实现对含能材料热分解行为的精确描述，并获得准确的热分解动力学参数；结合热分解动力学模型和环境⁃体系热平衡方程，求解含能材料在等温、非等温、绝热等多种温度条件下的热安全性；还可进一步对带包装的大批量样品的热安全性进行评估和预测。

然而，该方法仍存在诸多问题与挑战，主要表现在以下几个方面：

（1）在热分解动力学参数的求解方法上，存在是选择无模型法还是基于反应模型法的争议。无模型方法求解过程简单，易于实现，但是该方法不考虑热分解反应为单步或多步，N级或自催化反应等问题，，不能给出确切的反应机理模型。而基于反应模型的方法存在模型选择错误的风险，因此必须预先确定反应的基本类型，并结合已有的化学反应机理对热分解模型进行构造，同时该方法求解过程复杂，计算量较大，需专业的分析软件辅助。

（2）热分解动力学对含能材料开展热安全性评价尤其要重视样品状态、实验技术、评价目标之间匹配的问题。例如，针对某些具有熔融分解特征的含能材料，其在非等温条件下发生分解放热时实际处于固⁃液共存状态，基于该状态获得的动力学参数并不能准确描述相对低温下的固相分解过程，也即在这种情况下不能将高温下获得的动力学模型直接用于相对低温下热安全性的预测。

总之，如何基于小药量的热分析结果，开展对大批量含能材料的热安全性评价，一直是热安全研究领域关注的核心问题。基于热分解动力学对含能材料开展热安全评价在研究对象上具有更强的灵活性，一旦获得了准确的热分解动力学参数，则可开展含能材料在复杂温度条件下的热安全性评价，有利于弥补大型热失控实验时间和经济成本高等问题。同时，在建立热安全性理论评估方法的基础上，有必要结合已有的大型热失控实验结果，与理论模拟结果进行比较，进一步验证理论评估方法的正确性。最后，对于一些尚处于实验室阶段的新型含能材料，合成量较少，无法满足大型热失控实验的样品量要求，因此基于理论评估的手段将是未来新型含能材料热安全性评估的必要选择。