内爆炸载荷下梯度泡沫铝夹芯管的动态响应*

张鹏飞，刘志芳，李世强

（太原理工大学机械与运载工程学院应用力学研究所，山西 太原 030024）

多孔材料能在几乎恒定的平台应力下经历极端塑性变形，在压溃至稳定阶段或破坏之前可以吸收大量的能量。然而，多孔材料相对较低的刚度和强度使其不适合单独用于抗冲击结构，而更适合作为夹芯结构的芯层材料[1-2]。

与单一结构相比，多孔材料夹芯结构在爆炸载荷下能够表现出更优异的抗爆性能[3-4]。圆柱壳是一种常用的爆炸容器结构形式，在爆炸防护工程中应用广泛。夹芯结构面板的厚度、芯层相对密度和厚度、胞孔类型等是影响其响应的主要物理参数，Liu 等[5]指出，对于夹芯管，内板厚度应不大于外板厚度，这样能在降低夹芯管整体变形的同时更能发挥泡沫铝芯层的吸能优势。Nurick 等[6]和Karagiozova 等[7]通过实验和数值模拟，对比了蜂窝芯层夹芯板和空气芯层夹芯板的力学行为，发现高载荷下蜂窝芯层夹芯板的抗爆性能更优；芯层材料相同时，传递至后面板的载荷与爆炸载荷强度及芯层厚度有关。Karagiozova 等[8]指出，在质量保持一定的情况下，泡沫芯层相对密度较低的夹芯管抗爆性能优于单层圆管，相对密度较高的泡沫芯层夹芯管外管变形量大于单层圆管。

夹芯结构的芯层具有很强的设计性，在芯层中引入梯度后，结构的力学性能得到了进一步提升，梯度芯层比普通芯层更能发挥芯层材料的吸能特性。Shen 等[9]提出，当夹芯结构的芯层梯度分别为正梯度和负梯度时，结构在变形过程中会出现一个冲击波和双重冲击波。Gardner 等[10]研究了梯度泡沫夹芯梁在冲击波作用下的动态力学行为，实验结果表明，梯度泡沫芯层层数的增加会减小芯层间阻抗的不匹配，并提高结构的抗冲击性能。Liang 等[11]通过实验和二维Voronoi 技术数值模拟研究了爆炸载荷下双层泡沫铝夹芯板的动态响应和能量吸收，结果表明，正梯度泡沫试件吸收的能量和传递到背板的冲量最多，负梯度泡沫试样吸收的能量和传递到背板的冲量最少。

大多数常用的多孔材料有限元模型，通常基于理想化的实体单元建模，因此无法解释多孔材料微结构的动态变化。范志庚等[12]建立了泡孔形状规则的有限元模型，并分析了泡孔形状、孔隙率等因素对泡沫材料力学性能的影响。Zhang 等[13]应用3D-Voronoi 技术生成闭孔泡沫模型，对梯度泡沫在不同冲击速度下的压缩特性和变形机理进行了数值研究。Liang 等[14-15]对内爆炸载荷下的泡沫铝夹芯管进行了实验研究和数值模拟，他们基于二维Voronoi 算法构建了泡沫铝芯层并进行了参数研究，结果表明外管的最大变形量与泡沫芯层的相对密度、梯度有关，内管壁厚对夹芯管结构的能量吸收影响很大。

为研究梯度夹芯圆管结构在爆炸载荷下的动力响应特征及其与芯层细观结构间的关系，本文中利用3D-Voronoi 技术，建立梯度泡沫铝夹芯管有限元模型，研究内、外管厚度、芯层的相对密度、梯度泡沫芯层以及炸药当量等参数对内爆炸载荷作用下夹芯管动态响应的影响。

1 有限元模拟

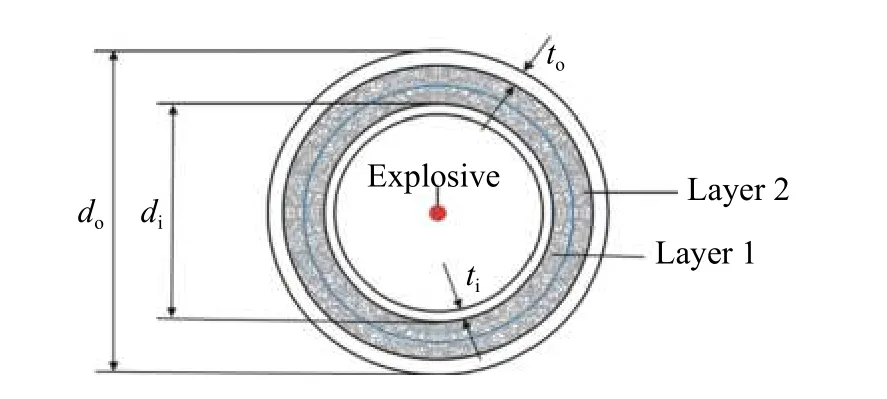
图1 泡沫铝夹芯管示意图Fig. 1 Schematic diagram of sandwich tube with gradient foam aluminum cores

1.1 夹芯管有限元模型

泡沫铝夹芯管结构由泡沫铝芯层和内、外两个同心的薄壁金属圆管三部分组成。图1 给出了泡沫铝夹芯管示意图，外管直径为do、壁厚为to，内管直径为di、壁厚为ti，长度为L。内外管之间填充泡沫铝芯层，梯度泡沫铝夹芯管的芯层由两个厚度相同、相对密度不同的芯层1 和芯层2 组成。

1.1.1 3D-Voronoi 泡沫模型

3D-Voronoi 随机模型能够描述真实多胞材料的复杂细观结构，因而在多胞材料的力学性能分析中应用广泛。Voronoi 图形是将三维的离散点集进行空间划分，形成每个点所对应的多面体形状的Voronoi 区域，每个区域是距离对应点（形核点）最近的一个空间点的集合。生成3D-Voronoi 模型的步骤为：首先在体积为V 的空间中随机分布N 个形核点。对于任意一个形核点，该形核点与其附近所有相邻的形核点所围成的空间称为胞元，整个空间中共有N 个胞元。同时，为了避免生成体积过小的胞元，规定任意两个形核点之间的距离不得小于δ（δ≥0）[13]，其中δ 为任意两形核点之间的最小距离。在体积为V0且含有N 个正十四面体胞元的立方体中，任意两个形核点之间的距离如下：

将泡沫的不规则度定义为k，表达式如下：

当k=0 时，表示生成的立方体由N 个正十四面体胞元组成；当k=1 时，表示生成完全随机的三维Voronoi 结构。本文中，泡沫不规则度k=0.2[13]。

将由上述理论生成的三维闭孔泡沫铝模型（见图2（a））导入软件HYPERMESH 中进行处理并切割为圆管形状（见图2（b）），芯层胞元平均直径约4.4 mm。

图2 泡沫铝夹芯管的建模过程Fig. 2 Process of constructing aluminum foam-cored sandwich tube model

1.1.2 夹芯管有限元模型

采用有限元软件LS-DYNA 对泡沫铝夹芯管结构在内爆炸载荷作用下的动态响应进行数值模拟。空气和炸药采用8 节点Solid 164 实体单元；内、外圆管采用4 节点 Shell 163 壳单元；泡沫铝芯层采用S3R 和S4R 壳单元两种单元类型。建立的有限元模型如图2（c）所示，内管、外管与泡沫铝芯层之间采用自动面面接触，泡沫铝芯层采用单面自接触。为了减小网格不良划分的影响，利用初始体积分数法将炸药材料填充到空气结构中，泡沫铝夹芯管与空气及炸药之间采用流固耦合算法。由于结构和加载的对称性，模拟中采用四分之一模型，在两个截面处施加对称约束，其余各面为无反射边界条件。

1.2 材料属性

假设夹芯管内外圆管的材料为AISI 1045 钢，考虑应变率效应的影响，本构关系采用Johnson-Cook 模型（J-C 模型），表1 为J-C 模型材料参数。泡沫铝对应变率效应不敏感，因此材料模型选用了双线性弹塑性模型，密度为2 730 kg/m3、杨氏模量为70 GPa、泊松比为0.3、屈服强度为190 MPa。采用*MAT_NULL 材料模型来描述空气材料的本构模型，采用多线性状态方程来描述:

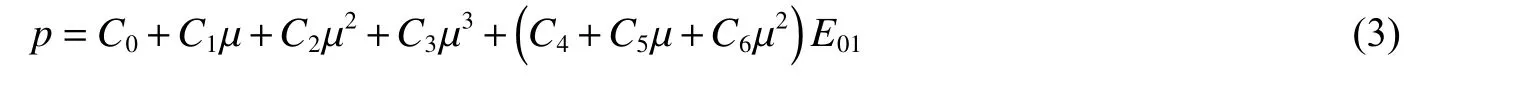
式中：C0、C1、C2、C3、C4、C5、C6为常数，E01为空气初始比内能，如表2 所示。

表1 J-C 模型材料参数[14]Table 1 Material parameters of J-C model

表2 空气材料参数Table 2 Material parameters of air

炸药的爆轰过程采用JWL 状态方程进行数值模拟，其表达式如下：

式中: A、B、R1、R2、ω 为常数，E02为炸药初始比内能，V 为单位体积炸药的初始相对体积。表3 为炸药的材料参数。

表3 炸药的材料参数[14]Table 3 Material parameters of explosive

模拟分析中考虑了均匀泡沫铝芯层与梯度泡沫铝芯层夹芯管结构，均匀泡沫铝芯层相对密度分别为11%、14%和17%，为保证夹芯管试件总质量不变，试件WT1-WT5 内外管采用了不同的壁厚，WT6、WT7 采用了不同芯层相对密度，详细的参数如表4 所示。梯度泡沫铝芯层夹芯管试件几何参数如表5所示。所有夹芯管试件的长度均为61 mm，炸药长径比为1.5∶1。

表4 泡沫铝夹芯管的几何参数Table 4 Geometric parameters of sandwich tubes with foam aluminum cores

表5 梯度泡沫铝夹芯管的几何参数Table 5 Geometric parameters of sandwich tubes with gradient foam aluminum cores

1.3 有限元模型验证

1.3.1 网格敏感性验证

网格密度对数值模拟结果的精确性有直接影响，较大的网格尺寸会降低模拟的准确性，较小的网格尺寸耗费计算机资源，因此，必须找到一个合适的网格尺寸。图3 给出了试件WT2 不同网格尺寸内、外管变形量的时程曲线。

由图3 可知，当网格尺寸为5 mm 时，数值模拟结果与其他网格尺寸的模型存在显著差异，有限元模型的准确性较差。当网格尺寸为1、2、3 mm 时，内管的最大变形量重合，而外管的最大变形量也基本重合，最大差异为1%。因此，数值模拟中采用2 mm 的网格。

1.3.2 数值模拟与实验结果对照

为了验证有限元模型的正确性与合理性，与文献[14]中的三组实验结果（T1、T7、T8）进行了对比，T1、T7 和T8 三组试件几何参数如表6 所示，内、外管壁厚为1.5 mm。图4 为数值模拟与实验结果变形模式的对比。表6 给出了试件内、外管最大变形量的实验结果与数值模拟结果。由此可知，试件数值模拟的结果和实验结果吻合较好，从而验证了有限元模型的合理性与可行性。

图3 不同网格尺寸的内、外管变形量Fig. 3 Deformation of inner and outer tubes with different mesh sizes

表6 数值模拟与实验结果的对比Table 6 Comparison between numerical simulation and experimental results

图4 数值模拟与实验结果对照图Fig. 4 Comparison between numerical simulation and experimental results

2 结果与分析

夹芯管结构内外管的最大变形量和吸能性是评估夹芯管结构抗爆性能的重要指标。为了排除质量的干扰，对内外管的最大变形量进行如下处理[13]：

式中：δT为内管/外管的变形量，mT和rT分别为内管/外管的质量和半径。

比吸能Esa(specific energy absorption)定义为单位质量结构所吸收的能量，可由下式给出：

式中：Ea为结构吸收的能量，M 为结构的质量。

2.1 泡沫胞元数量和胞元壁厚的影响

在泡沫铝的3D-Voronoi 模型中，其相对密度的改变有两种方法，第一种方法是通过保持胞元壁厚不变，改变单位体积的形核点数，随着单位体积的胞元数量的变化，单个泡沫胞元的总体积将会增大或减小；第二种方法是保持单位体积的形核点数不变，改变胞元的壁厚。以相对密度为14%的泡沫芯层作为基准，通过两种方法构建相对密度为11%及17%的泡沫芯层，并进行内爆炸载荷下夹芯管动态响应的数值模拟。图5 给出了两种方法得到的不同相对密度泡沫铝夹芯管WT2、WT5 和WT6 的内、外管的变形量时程曲线，其中WT2（1）和WT7（1）为改变胞元数量的模型，WT2（2）和WT7（2）为改变胞元壁厚的模型。由图5 可知，两种方法建立的泡沫铝夹芯管WT2 与WT7 在内爆炸载荷作用下内管与外管的变形量时程曲线基本重合，表明用这两种方法改变泡沫芯层相对密度构建的3D-Voronoi 模型效果相同。在后续的模拟分析中，芯层相对密度的改变均采用改变胞元壁厚的方法来构建。

图5 泡沫胞元大小和胞元壁厚对模型的影响Fig. 5 Effect of foam cell size and cell wall thickness on the model

从图5 也可以看出，随着芯层相对密度的增加，内管的变形量减小，外管的变形量增加。试件WT2 内管的变形量为10.80 mm，而WT7 内管的变形量为9.40 mm；试件WT2 外管的变形量为1.67 mm，而WT7 外管的变形量为1.93 mm。原因是芯层相对密度越大，抵抗变形的能力越强，因此减小内管的变形量而增大了外管的变形量。

图6 所示为不同相对密度泡沫铝芯层夹芯管的总吸能和比吸能图。由图6 可知，随着泡沫芯层相对密度增大，夹芯管中内管总吸能减小，芯层和外管的总吸能增大；内管和芯层的比吸能减小，而外管的比吸能增加，如试件WT2 内管的比吸能比试件WT7 内管的比吸能降低21%，而泡沫铝芯层的比吸能降低25%。模拟结果表明内爆炸载荷作用下，泡沫芯层的相对密度是影响结构吸能的主要因素之一，相对密度越小，芯层和内管的塑性变形越大，而外管的变形量越小，因此填充较小相对密度芯层的夹芯管其抗爆炸性能较优。

图6 不同相对密度的泡沫铝夹芯管总吸能和比吸能Fig. 6 Ea and Esa of sandwich tubes with different relative density foam cores

2.2 内外管壁厚的影响

在保持内、外圆管总质量不变的情况下，研究在不同炸药量下内、外圆管的壁厚对泡沫铝夹芯管抗爆性能的影响。图7 给出了不同炸药量下5 个夹芯管内、外管的最大变形量曲线，由图7 可知，随着炸药量的增加，夹芯管内、外管的变形量增加。因为炸药量越大，施加到夹芯管结构上的冲量越大，结构的变形就越大。由图7（a）可知，随着夹芯管内管壁厚的增加，内管变形量减小。内管的壁厚越大，抵抗变形的能力就越强，所以内管的变形量减小。由图7（b）可知，当炸药量小于等于16 g 时，外管的变形量先减小后增大，且5 种不同内、外管厚度配置的夹芯管试件中，达到外管变形量最小值的试件不同，如炸药量为12 g 时，试件WT2 的变形量最小，而炸药量为16 g 时，试件WT4 的变形量最小。炸药量为18 g 时，外管的变形量持续减小。

图7 不同壁厚比对内、外管变形量的影响Fig. 7 Effect of different wall thickness ratio on deformation of inner and outer tubes

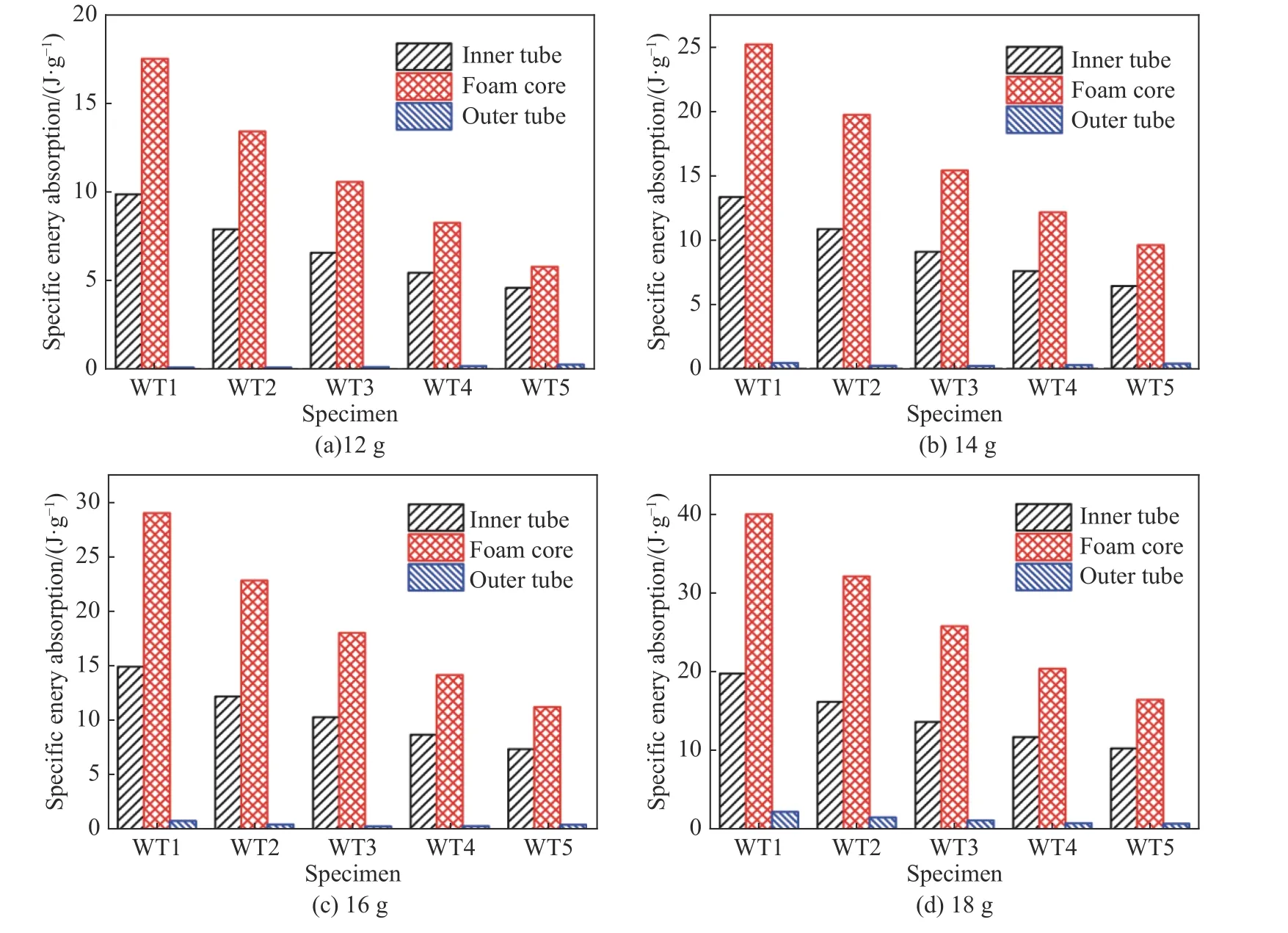
图8 不同炸药量下夹芯管的Esa 图Fig. 8 Esa of the sandwich tube under different explosives

图8 所示为4 种不同炸药量下内、外管的壁厚对泡沫铝夹芯管比吸能的影响。随着爆炸载荷的增加，夹芯管结构各部分的比吸能增加；相同爆炸载荷作用下，随着夹芯管内管壁厚的增加，内管和芯层的比吸能减小；而外管的比吸能则与爆炸载荷有关，如炸药量为14 g 时，试件WT3 外管的比吸能最小；炸药量为18 g 时，试件WT5 外管的比吸能最小。

不同爆炸载荷下内、外圆管的壁厚对泡沫铝夹芯管的抗爆性能模拟结果表明，保持夹芯管质量不变的情况下，内、外管壁厚的改变对夹芯管的变形和吸能有显著影响，随着爆炸载荷的增加，夹芯管结构内外管的变形和比吸能增加。内管壁厚越小，夹芯管结构内管的变形量越大，吸收的能量越多；外管的变形量和比吸能与爆炸载荷的大小有关，呈现先减小后增大的趋势。

2.3 梯度泡沫芯层的影响

由两层厚度相同、相对密度不同的泡沫铝构成夹芯管的梯度芯层（见图1），在保持泡沫芯层总质量不变的情况下，建立了负梯度芯层夹芯管N-WT1，均匀芯层夹芯管U-WT2 和正梯度芯层夹芯管P-WT3三种不同的有限元模型。负梯度夹芯管是指与内管相邻的芯层1 的相对密度小于芯层2 的相对密度，正梯度则相反，均匀芯层夹芯管是两层芯层的相对密度相同，具体参数见表5。

图9 给出了梯度泡沫铝芯层夹芯管在内爆炸载荷下不同时刻的变形模式图。爆炸载荷作用下，负梯度夹芯管中泡沫芯层1 首先被压实，之后芯层2 被压实。正梯度夹芯管中泡沫芯层1 部分被压实后，在两层泡沫芯层的交界处芯层2 部分被压实，之后芯层1 的压实层和芯层2 的压实层同时被压实。

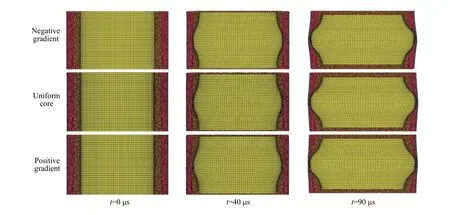
图9 梯度夹芯管变形过程Fig. 9 Deformation process of sandwich tube with gradient foam aluminum cores

在t=40 µs 时，正梯度夹芯管内侧泡沫层压缩量明显小于均匀模型，原因是正梯度夹芯管中芯层1具有较大的相对密度，具有较强抵抗变形的能力。图10 给出了梯度芯层夹芯管外管的变形量随时间的变化规律与夹芯管各部分的比吸能。由图10 可知，正梯度夹芯管外管的变形量比负梯度夹芯管降低27%；正、负梯度夹芯管各部分的比吸能明显大于均匀泡沫芯层夹芯管各部分的吸能，负梯度泡沫芯层各部分的比吸能最大。在相同的内爆炸载荷作用下，综合考虑外管的变形量及结构的比吸能，正梯度夹芯管的抗爆性能最优。

2.4 芯层相对密度的影响

图11 为不同炸药量下双层圆管WT0 与泡沫铝夹芯管WT2、WT6 和WT7 内、外管的变形量-时间曲线。以爆炸载荷作用下双层圆管的内管与外管正好接触的炸药量作为基准，数值模拟的结果分为以下两类：（1）炸药量较小时，双层圆管结构主要由内管承受爆炸载荷，外管没有明显的塑性变形。夹芯管结构的外管发生了较大的塑性变形，这是由于泡沫芯层能够通过胞元结构将爆炸载荷传递到外管；（2）增大炸药量后，双层圆管结构的内管冲击外管，传递动量，外管产生塑性变形，且外管的变形量随着炸药量的增加而明显增大。而夹芯管结构由于具有更大的质量且泡沫芯层可以通过弯曲和压缩吸收能量，导致夹芯管外管的变形增加量小于双层圆管结构。所以炸药量为8.5 g 时，双层圆管结构的变形量低于夹芯管结构；炸药量为10 g 时，双层圆管的变形量比相对密度17%的泡沫铝夹芯管的变形量高了27%。对比不同炸药量下的双层圆管结构与夹芯管结构的内、外管变形量，发现填充泡沫芯层可以有效减小内管的塑性变形，且随着泡沫芯层相对密度的增大，夹芯管结构内管的变形量呈下降趋势，外管的变形量呈上升趋势。

图10 梯度夹芯管外管变形量随时间的变化规律和夹芯管各部分的比吸能Fig. 10 Outer tube special deformation and specific energe absorption of sandwich tubes with gradient foam aluminum cores

图11 不同炸药量下的双层圆管与泡沫铝夹芯管的变形量-时间曲线Fig. 11 Special deformation-time curves of double-layer circular tubes and aluminum foam sandwich tubes under different explosives

3 结 论

基于3D-Voronoi 技术，建立了泡沫铝3D-Voronoi 模型及泡沫铝夹芯管的有限元模型。模拟结果与已有的实验结果进行了对比，验证了所建立模型的合理性。在此基础上，研究了内爆炸载荷下夹芯管的动态响应，分析了夹芯管内、外管的壁厚，泡沫芯层的梯度，泡孔大小及壁厚等参数对泡沫铝夹芯管力学性能的影响，并与双层圆管进行了对比。主要结论如下：

（1）内爆炸载荷作用下，保持内、外圆管总质量不变，随着内管壁厚的增大，内管的最大变形量减小，而外管的最大变形量先减小后增大，泡沫芯层吸收的能量减小；

（2）泡沫铝3D-Voronoi 模型中，泡沫芯层的相对密度可以通过泡沫胞元大小和胞元的壁厚来控制，对于结构的变形量和能量吸收等宏观响应结果，两种方式下获得的数值模拟效果一致；

（3）三种梯度芯层夹芯管的内爆炸研究表明，相同爆炸载荷下正负梯度泡沫芯层的比吸能均高于均匀泡沫芯层夹芯管的比吸能，正梯度夹芯管的外管变形量最小，三种梯度芯层夹芯管中正梯度泡沫芯层夹芯管的抗爆性能最好；

（4）不同炸药量下，双层圆管与三种相对密度泡沫铝夹芯管的变形模式不同。随着炸药量的增加，内管与外管的最大变形量增大；与双层圆管相比，泡沫芯层的填充降低了内管的最大变形量，而对外管最大变形量的影响则与爆炸载荷的大小有关。