世锦赛视角下男子田赛跳跃类项目发展与成绩预测研究
郭树君,曹 杰
世界田径锦标赛(以下简称世锦赛)自1983年举办以来,极大地推动了世界各国田径运动的发展。笔者统计了中国代表队在12-16届中的表现,跳跃类项目积39分,而投掷类项目积0分,跳跃类项目发展远胜于投掷类项目发展。研究世锦赛田赛跳跃类项目运动成绩,一方面可以使我们了解当今世锦赛田赛跳跃类项目发展水平,另一方面也能了解我国男子田赛跳跃类项目到底处在什么样的一种发展水平。因此研究世界田径锦标赛男子田赛跳跃类项目的发展显得颇为重要。黄海平、曲淑华、车超主要通过平均递进系数、标准差和平均值等统计学指标去反映运动成绩的走向。曲淑华、王秀军运用灰色系统理论建立GM(1,1)模型去预测世锦赛夺冠成绩,而这种模型需要的样本数据比较少,且局限性少,计算简便,检验方便。本文则是从平均值、递进系数和标准差三个研究指标去描述世锦赛男子田赛跳跃类项目运动成绩发展,通过建立GM(1,1)模型并利用matlab数学建模软件实现2021年第18届世锦赛的成绩预测。
1 研究对象与方法
1.1 研究对象
以第1-17届世界田径锦标赛田赛跳跃类项目(跳远、三级跳远、跳高、撑竿跳高)前八名运动员运动成绩为研究对象。
1.2 研究方法
1.2.1 文献资料法
访问国际田联官方网站,获得第1-17届(1983年第1届-2019年第17届)世界田径锦标赛男子田赛跳跃类四个项目(跳远、三级跳远、跳高、撑竿跳高)前八名运动员成绩。访问中国知网,以“世界田径锦标赛”、“发展”、“成绩预测”等关键词进行检索,整理汇总与本论文研究内容相关的资料。
1.2.2 数理统计法
使用Word统计出每届各项目第一名成绩、前三名的平均成绩、前八名的平均成绩、前八名成绩的标准差。采用递进系数公式,D=(X-Y)/Y×100 (D递进系数;X本届世锦赛前8名平均成绩;Y前一届世锦赛前8名平均成绩),反映田径项目总体的发展趋势。
1.2.3 比较分析法
对第1-17届世锦赛标田赛项目男子跳跃类项目进行横向纵向比较分析。
1.2.4 灰色预测法
运用 GM ( 1,1 )灰色预测模型思想,利用数学建模Matlab软件分析,预测2021世锦赛男子田赛跳跃类项目第一名的成绩。
2 研究结果与分析
2.1 田径世锦赛男子田赛跳跃类项目发展态势分析
2.1.1 世锦赛男子跳远项目成绩变化特征分析

图一 历届世锦赛跳远项目前八名运动员成绩曲线(单位:m)
历届世锦赛男子跳远夺冠成绩在第3届取得最高值,成绩为8.95m,在第9届取的最低值,成绩为8.32m。整体成绩也在第三届取得最高值,成绩为8.32m,在第四届取得最低值,成绩为8.10m,差值为0.22m。自第3届美国选手Mike powell创造出8.95m的世界纪录以来,跳远项目发展缓慢,之后的历届成绩距离世界纪录的差值最小为0.25m,仍有较大差距,短时间内没人能突破这个成绩。整体的发展趋势为:1-3届逐步发展高峰期,4-9届处于低谷期,10-14届稳定期,15-17处于暂时的波动期,整体呈现稳定的缓慢上升趋势。
第1-17届世锦赛男子跳远前8名运动员平均成绩的递进系数均值为0.10,说明整体上男子跳远项目成绩呈现上升趋势。第1、3、6、9、14、15个递进系数绝对值相对较大,表明第1-2、3-4、6-7、9-10、14-16届平均成绩波动较大;第10、12、13、14、16届运动员整体水平较高且标准差相对较小,可知第10、12、13、14、16届男子跳远项目竞争的确激烈。
总的来说:世锦赛跳远项目经历了短时间的增长和较长时间的低谷和平稳发展,总体呈缓慢波动上升的一个趋势。
2.1.2 田径世锦赛男子三级跳远项目成绩变化特征分析
历届世锦赛三级跳远夺冠成绩在第5届取得最高值,成绩为18.29m,在第1届取的最低值,成绩为17.42m,差值为0.87m;平均成绩在第13届取得最高值,成绩为17.46m,在第1届取得最低值,成绩为17.09m,差值为0.37m,差值较大受到第一届成绩影响。自从第五届世锦赛英国选手jonathan Edwards创造世界纪录18.29米以来,只有两人闯进18.00m,分别为15届美国选手christian Taylor的18.21m和14届法国选手teddy Tamgho的18.04m,间接表明三级跳远发展缓慢。整体的趋势为:除首届以外,整体平均成绩在17.20-17.40之间波动,第2-12届波动较小,13-17届波动较大,整体成绩呈现稳定的缓慢增长趋势。
第1-16届世锦赛男子三级跳远前8名运动员平均成绩的递进系数均值为0.14,说明整体上男子三级跳远项目成绩呈现上升趋势。第1、12、13、16个递进系数绝对值较大,表明第1-2、12-14、16-17届成绩波动较大;第2、4、6、13届运动员整体水平较高且标准差相对较小,可知第2、4、6、13届男子三级跳远项目竞争的确激烈。
总的来说:三级跳远项目整体成绩经历了稳定的慢增长和慢下降交替,成绩波动较小过渡到波动较大,总体呈现缓慢波动上升的趋势。
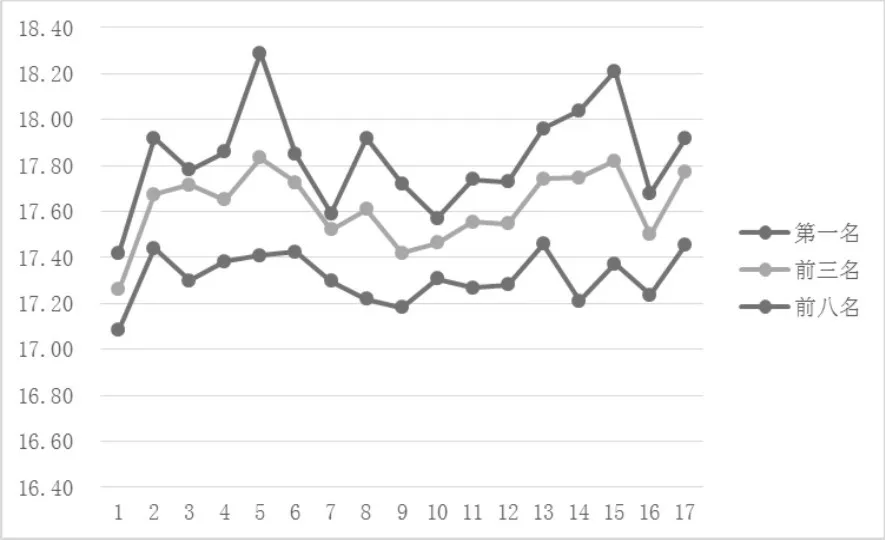
图二 历届世锦赛三级跳远项目前八名运动员成绩曲线(单位:m)
2.1.3 田径世锦赛男子跳高项目成绩变化特征分析
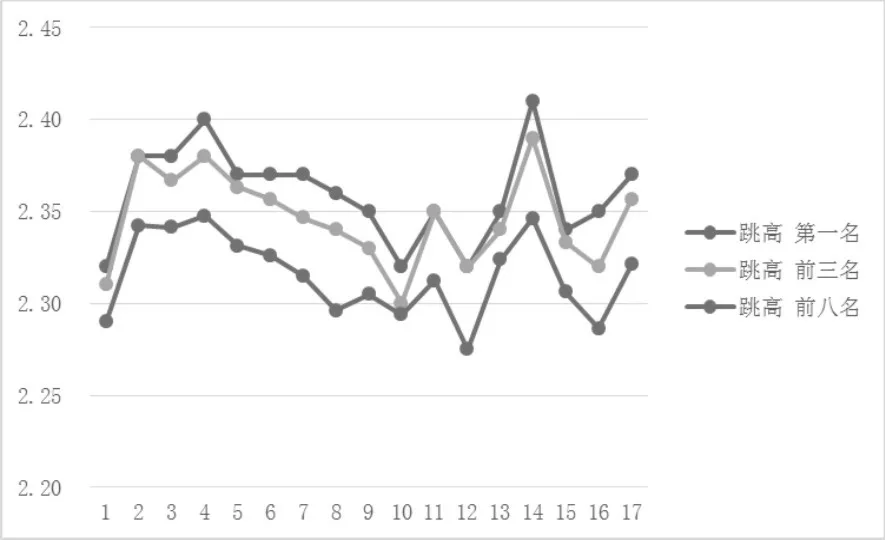
图三 历届世锦赛跳高项目前八名运动员成绩曲线(单位:m)
历届世锦赛跳高夺冠成绩在第14届取得最高值,成绩为2.41m;在第1届取的最低值,成绩为2.31m,差值为0.10m,成绩较为稳定平均成绩在第4届取得最高值,成绩为2.35m,在第12届取得最低值,成绩为2.28m,差值为0.08m。整体的趋势为:1-4届到达高峰,5-12届逐渐下降到最低值,13-14届上升到最高峰,15-16届大幅下降,17届大幅上升的局面。
第1-17届世锦赛男子跳高前8名运动员平均成绩的递进系数均值为0.09,说明整体上男子跳远项目成绩呈现上升趋势。第1、11、12、14、16个递进系数绝对值较大,表明第1-2、11-13、14-15、16-17届成绩波动较大。第3、4、6、13届运动员整体水平较高且标准差较小,可知第3、4、6、13届男子跳高项目竞争的确激烈。
总的来说:跳高项目整体发展经历了短时间的增长,再到长时间的稳定下降,再到短时间的增长和下降的局面。
2.1.4 田径世锦赛男子撑竿跳高项目成绩变化特征分析
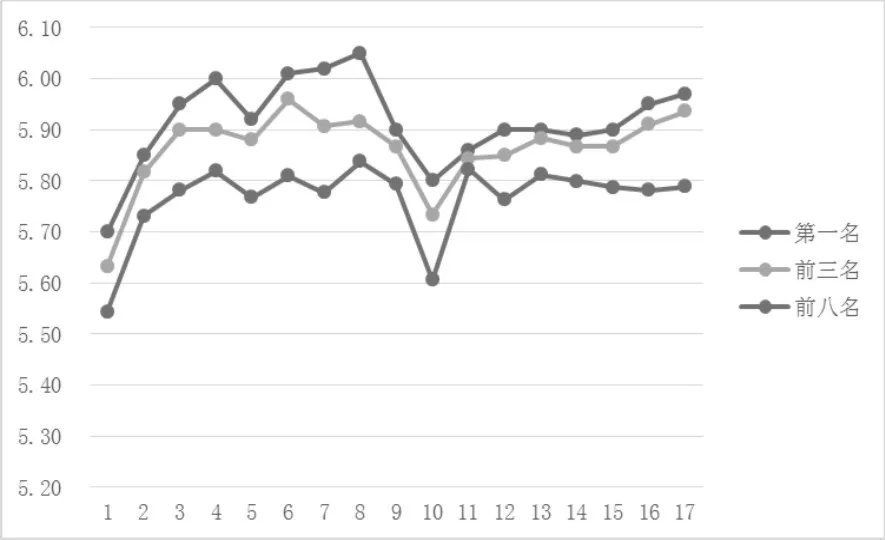
图四 历届世锦赛男子撑竿跳高项目前
历届世锦赛男子撑竿跳高夺冠成绩在第8届取得最高值,成绩为6.05m,在第1届取的最低值,成绩为5.70m,差值为0.35m,夺冠成绩从1-8届发展迅速,9-10届跌入低谷,11-17届稳步发展;平均成绩在第8届取得最高值,成绩为5.84m,在第1届取得最低值,成绩为5.54m,差值为0.30m。整体的趋势为:除了第1、10届成绩较低外,整体平均成绩在5.80左右起伏的局面。
第1-17届世锦赛男子撑竿跳高前8名运动员平均成绩的递进系数均值为0.28,说明整体上男子撑竿跳高项目成绩呈现上升趋势;第1、7、9、10、11递进系数绝对值较大,表明第1-2、7-8、9-12届成绩波动较大。第4、8、9、11、13、14、15届运动员整体水平较高且标准差相对较小,可知第4、8、9、11、13、14、15届男子跳高项目竞争的确激烈。
总的来说:撑竿跳高项目除了第1、10届整体成绩稳定在5.80左右,呈现稳定的缓慢上升趋势。
2.2 2021年第18届世锦赛田赛项目第一名成绩预测
本文则是用观察到的反映世锦赛田赛跳跃类项目成绩特征的时间序列来构造灰色预测模型,预测下一届世锦赛田赛跳跃类项目成绩特征。使用邓聚龙教授提出的均值GM(1,1)灰色模型(EGM模型较其它模型适用于振荡序列),对第17届世锦赛男女子田赛项目第1名成绩进行建模预测分析。(X(0)为预测序列,x(0)为实际序列)。
以男子跳高项目为例,统计近五届世锦赛男子跳高项目第一名成绩,运用均值GM(1,1)灰色模型对第18届世锦赛男子项目第1名成绩进行预测:
第一步:获取第13届至17届世锦赛男子跳高项目第一名成绩作为原始序列,x(0)(k)=[2.35,2.41,2.34,2.35,2.37];
第二步:对原始数据进行一次累加,得到一次累加序列,
x(1)(k)=[2.35,4.76,7.10,9.45,11.82];
第三步:对累加序列进行紧邻均值生成,得到紧邻均值序列,
z(1)(k)=[3.5550,5.9300,8.2750,10.6350];
第四步:用最小二乘法对参数向量A进行估计,其中A=(BTB)-1BTY;运用matlab软件计算求得,发展系数 a=0.0047,灰色作用量 b=2.4007;

第五步:均值GM( 1,1)模型的时间响应式为: X(1)(k) =[x(0)(1)- b/a] e-ak+b/a,即X(1)(k)=-508.4372e-0.0047k+510.7872;
第六步:按 X(0)(k)=[X(1)(k)-X(1)(k-1)],k=2,3,4,5 ,将预测数据还原,计算出预测值X(0)(2) =2.3841,X(0)(3)=2.3730,X(0)(4)=2.3619,X(0)(5)=2.3509。
第七步:采用相对误差法去检验模型精度。
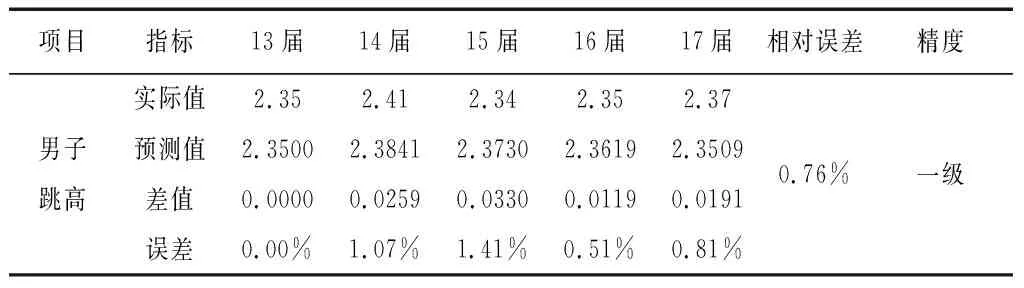
表1 近五届世锦赛男子跳高项目相对误差表
本文的模拟值与原始值的平均相对误差为0.76%,小于1%,模拟的精度为一级,所以从这一方面考虑,本文相对模拟误差较小,精度较高,模型较好,能够较好地预测第 18届世锦赛男子跳高成绩。
第八步: 根据预测模型,计算得第 17届世锦赛女子铅球第1名成绩预测值为X(0)(6) = 2.3399,即预测值为2.34m。
根据上述分析步骤,预测其他三个项目的冠军成绩,其中跳远误差0.84%、三级跳远误差0.66%、跳高误差0.76%、撑竿跳高0.09%,相对误差均小于1%,预测模型的成绩精度均在一级以上,模拟的预测数据较好。根据数据显示,第18届世锦赛田赛跳跃类项目的夺冠预测成绩分别为:男子跳远8.65m、男子三级跳远17.74m、男子跳高2.34m、男子撑竿跳高6.00m.

表2 男子田赛跳跃类项目预测方程精度与预测成绩值(单位:m)
2.3 我国男子田赛跳跃类项目发展态势
2.3.1 我国男子跳跃类优秀运动员基数小
目前,还未有中国人在男子田赛跳跃类项目中获得金牌,获得奖牌的相对也较少。朱建华在第一届世锦赛以2.29m获得第三名;张国伟在第15届世锦赛上以2.33m获得第二名。王嘉男在第15届世锦赛以8.18m获得第三名。获得前八名名次的有12人,其中跳远8人、跳高2、撑竿跳高1人、三级跳远1人,前八名以外的名次有16人,三级跳远5人、跳高4人、撑高跳高4人、跳远3人。说明了我国男子田赛跳跃类优秀运动员基数小。
2.3.2 我国田赛跳跃类项目的发展情况为:跳远>跳高>三级跳远>撑竿跳高
总的来说,跳远项目发展最好,跳高项目较好,三级跳远次之,撑竿跳高最后。
2.3.3 我国田赛跳跃类项目呈现短期的同步发展
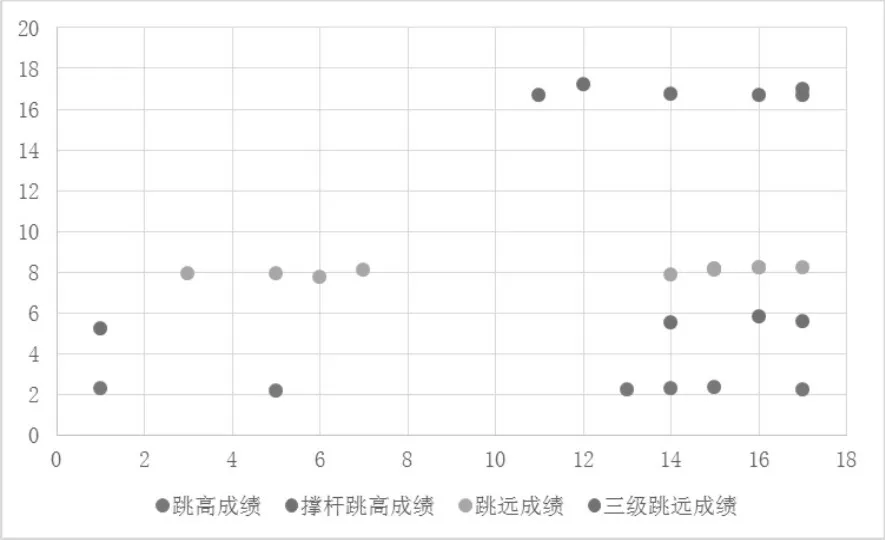
图五 历届男子田赛跳跃类项目运动成绩散点图
我国田赛跳跃类项目的发展随着历届世锦赛的发展逐渐呈现出稳定的发展态势,自第14届世锦赛之后,我国田赛四个跳跃类项目历届挺进世锦赛人数增多,出现了短期上项目同步发展。相对于14届之前,我国的四个项目从未有过同步发展,只有跳远项目有过短时间的发展;而跳高、撑竿跳高、三级跳远项目发展落后,停滞不前。
2.3.4 我田赛跳跃类项目发展从“无法踏入世锦赛”到“能够踏入却无法取得优秀成绩”转变
近年来我国世锦赛男子田赛跳跃类项目的整体发展现状已经从大部分项目无法踏入世锦赛的大门转变到有能力踏入
世锦赛的大门但无法获得较高的运动成绩的转变,可见近几年我国田赛跳跃类项目发展有所建树,但是如何提高现有的水平,冲击更高的成绩和排名仍然需要运动员和教练员等多方面的努力。
3 结论
3.1 世锦赛田赛跳跃类项目发展态势
世锦赛田赛跳跃类四个项目整体水平呈现缓慢上升态势。跳远项目整体的发展趋势为:1-3届逐步发展高峰期,4-9届处于低谷期,10-14届稳定期,15-17处于暂时的波动期;三级跳远项目整体的发展趋势为:除首届以外,整体平均成绩在17.20-17.40之间波动,第2-12届波动较小,13-17届波动较大;跳高项目整体的趋势为:1-4届到达高峰,5-12届逐渐下降到最低值,13-14届上升到最高峰,15-17届波动下降的局面;撑竿跳高项目整体的趋势为:除了第1、10届整体成绩稳定在5.80左右,呈现稳定的缓慢上升趋势。
3.2 2021年第18届世锦赛田赛跳跃类项目预测值
第18届世锦赛田夺冠预测成绩分别为:男子跳远8.65m、男子三级跳远17.74m、男子跳高2.34m、男子撑竿跳高6.00m。
3.3 我国男子田赛跳跃类项目发展态势
我国男子田赛跳跃类优秀运动员基数小,项目的发展情况表现为:跳远>跳高>三级跳远>撑竿跳高,近几年我国田赛跳跃类项目呈现短期的同步发展,已从“无法踏入世锦赛”到“能够踏入却无法取得优秀成绩”转变。

