泉州湾河口湿地自然保护区综合效益模型构建与评价

叶 伟

(福建省林业勘察设计院,福州 350002)

红树林湿地作为滨海湿地中的重要组成,主要由植被、裸露滩涂,近海水域等组成,其在防浪护堤、生态调节、游憩观赏等方面中对滨海城市的作用尤为显著[1-4]。自20世纪中期以来,世界范围内越来越多的红树林湿地被围垦、破坏,其中仅我国的红树林分布面积就由42 001hm2(20世纪50年代)下降至14 877hm2(1997年)[5]。进入21世纪后,随着红树林湿地保护工作的开展,我国的红树林湿地面积又有稳步提升,至2013年,我国红树林分布面积又增加至34 472hm2[6]。随着红树林面积的动态变化,对于了解红树林湿地对沿海的生态环境、经济、人文的影响也都显得尤为关键,其中对于红树林湿地的综合效益评价对红树林湿地以及其周围地区的宏观发展都具有重要的意义。

林鹏等[7]、林惠来[8]、方耀垣[9]、林尤河[10]、叶维强等[11]学者于20世纪80年代在国内开始对红树林沿海湿地效益的评价及相关研究,其中方耀垣[9]对漳江口红树的生态和经济效益进行了定性的分析。张和钰等[12]、He等[13]利用模型构建的方评估湿地的效益,并将生态效益、社会效益、经济效益归入湿地效益体系中。Lin等[14]、池毓锋等[15]结合遥感和地理信息技术的手段对湿地的效益开展研究,从而将区域的效益进行空间制图,能更直观方便地展示,也能为管理提供依据。刘爱智[16]、庄大昌等[17]、评估了长时间效益的变化过程,从而将动态效益引入综合效益过程当中,强化了湿地效益需要考虑长时间的动态变化过程。其中,泉州湾保护区作为福建沿海湿地保护区的代表之一,游惠明等[18]、张臻等[19],对泉州湾的湿地效益做了不同的研究。本文以福建省泉州湾河口湿地自然保护区(下称泉州湾保护区)为例,应用遥感和地理信息手段,通过因子筛选分析建立一阶线性综合效益模型,计算2014，2016，2019年泉州湾保护区综合效益,同时引入空间统计分析方法分析综合效益的细化特征。通过综合效益的分析讨论该区域综合效益的变化趋势和细化特征,以期为泉州湾保护区的管理和未来发展提供参考依据,同时也能为后续研究提供方法和机理提供参考。

1 研究区概况

泉州湾保护区位于福建省泉州市,地处晋江、洛阳江入海口,被泉州的丰泽区、洛江区、晋江市、惠安县和石狮市环绕。地理位置为24°47′21.1″～24°59′50.9″N,118°42′8.1″～118°42′5.8″E,属于亚热带海洋性季风气候,多年平均气温20.4℃,年均降水量1 100mm,主要由红树林(Rhizophoraapiculata)、互花米草(Spartinaalterniflora)、滩涂等组成的湿地以及水域、人造环境所组成,该保护区主要承担了对红树林河口湿地的保护任务,是中国亚热带河口湿地的典型代表[20]。

2 研究方法

2.1 数据收集与获取

收集Landsat遥感影像,条带号119、行编号43,日期分别为2014年9月8日(云量6.66%)、2016年8月28日(云量4.25%)、2019年9月22日(0.08%)[21]。布设3个实验点,位置分别为：24°56′55″N,118°40′32″E；24°56′17″N,118°40′25″E；24°49′19″N,118°38′26″E,收集水质数据和泥质数据,走访泉州市物价局、泉州市气象局、泉州市生态环境局、泉州市水利局等相关职能部门收集泉州湾保护区矢量范围、经济数据、水文数据、气象数据、森林小班等基础资料。

2.2 数据预处理

预处理主要包括辐射定标、大气校正、融合、按研究区矢量裁剪、影像分类。其中影像的分类能将目标区域按照预期的研究方向,将影像的信息归类整合,得到更好的信息提取结果[21]。梯度推进机(Gradient Boosting Machines,GBM)属于机器学习中的决策树类型的一种,是一种将弱预测模型集成的机器学习技术。它使用了梯度提升方法,通过迭代训练新模型解决其他模型的弱点,从而改进效果。梯度推进机在许多应用的效果上比随机森林更好[22]。根据地面资料将泉州湾保护区按红树林、互花米草、滩涂、水域、其他进行种类划分,在影像中依据人工对比同期谷歌地球软件中的卫星影像和部分年限的森林小班数据提取不同地物类型像元灰度值点,并将提取的数值作为训练样本,对泉州湾保护区进行影像分类。得到2014，2016，2019年3幅泉州湾保护区的Landsat遥感影像。

2.3 综合效益模型构建

2.3.1指标选取

指标选取对于综合效益构建具有重要意义,依照科学性、系统、实用等原则,结合现有研究基础和学者观点[23-27],选取土地利用,归一化植被指数(NDVI)、森林植被净第一性生产力、森林固定CO2能力、水质污染指数作为生态效益的评价指标,国内生产总值、食物生产价值作为经济效益的评价指标,娱乐文化价值作为社会效益的评价指标。

2.3.2指标计算

土地利用评分以不同土地利用类型中NDVI和物种密度组成,在不同的土地利用类型中分别设置20个调查点,NDVI通过影像获取；物种密度通过设30m×30m样地,人工调查样地内所有物种数量的密度。通过比值计算将不同土地类型累计得分后获得评分,具体公式如下:

(1)

(2)

式中:LuccE为土地利用评分；Sv为物种密度；NDVI为比值植被指数；pred为Landsat卫星红光波段数据；pnir为近红外光波段数据。

水质污染指数采用污染指数法计算[28],污染指数是基于对单因子评价的基础上改进而来,将不同的水污染物实测值和对应的水污染物标准进行比较,计算单独的污染指数,然后将逐个单项污染指数通过加权平均、累加计算得到。具体公式如下:

(3)

式中:WP为水质污染指数；n为参与水质污染指数的单独的污染指数的数量；wi为第i项指标的权重；Ii为第i项单独的污染指数；Ci为单项污染指数的实测浓度；Si为与单项污染指数对应的水质指标的标准。最终计算而成的水质污染指数,能代表区域水环境的质量,其中P值越小,代表水质越好。

植被净第一性生产力(NPP)参照气候相关模型[29]以泉州湾保护区年均温度、年均降水量栅格数据库为基础,结合实际蒸散量计算的森林气候生产力,再辅以改正系数修正获得,具体计算公式如下:

E=

(4)

(1-e-0.0009585154×(E-30.02167))

(5)

式中:E为林地年实际蒸散量；P为林地年平均降水量；T为林地年平均气温；NPP(S)为由森林气候生产力计算的森林植被净第一性生产力；ai为植被覆盖度、树种组成、平均高、年龄和MNDWI指数评价因子权重；Ai为各评价因子得分值。

森林固定CO2能力据森林植被净第一性生产力物质量推算[30]；国内生产总值、食物生产价值、娱乐文化价值依据收集的资料整理获得。

将初选的8个指标因子原始数据根据标准差标准化处理后,建立因子之间的相关系数矩阵,计算各因子的特征值和方差贡献率。经过无量纲处理后,根据灰色关联分析中关联系数的公式计算出各指标因子间的关联系数,以一阶线性模型整理,获得综合效益模型。

2.4 空间统计分析

Local Getis Gi*方法能有效识别空间上的具有统计学意义的冷点和热点区域(热点代表高综合效益值(p<0.05)的统计显著聚集位置,冷点代表低综合效益值(p<0.05)的统计显著聚集位置[31],该方法应用领域较广,经常运用在与空间相关应用中[32-33]。首先，利用Moran I指数分析综合效益值的空间自相关,其中距离法采用曼哈顿距离(Manhattan Distance)。然后,使用Getis ord Gi*统计分析AOD的热点和冷点区域,距离的计算采用欧氏距离(Euclidean Distance)。空间自相关和Getis ord Gi*需要提供最佳的聚类阈值,为此,抽取逐期泉州湾保护区综合效益的4 000个空间点,运用增量空间自相关的方法确定最佳阈值[34],阈值的搜寻方法由30～240m,期间间隔为30m,距离计算方法采用欧氏距离,最终得到的最佳距离为150m。

3 结果与分析

3.1 影像分类结果与精度评价

影像分类的精度评价依照分类结果与参照样本比对的方法,依据谷歌地球2014年和2016年往期影像采集样本的空间坐标,通过实地采集2019年的1 500个点的坐标信息比对(样本含红树林、滩涂、水域、互花米草、其他共5类)；通过混淆矩阵将分类结果与验证结果比较,采用用户精度、生产者精度、总体精度、Kappa系数进行定量评价(表1)。其中验证点的选取规则结合网格布设规则,避免造成验证点由于过度集中而产生误差。

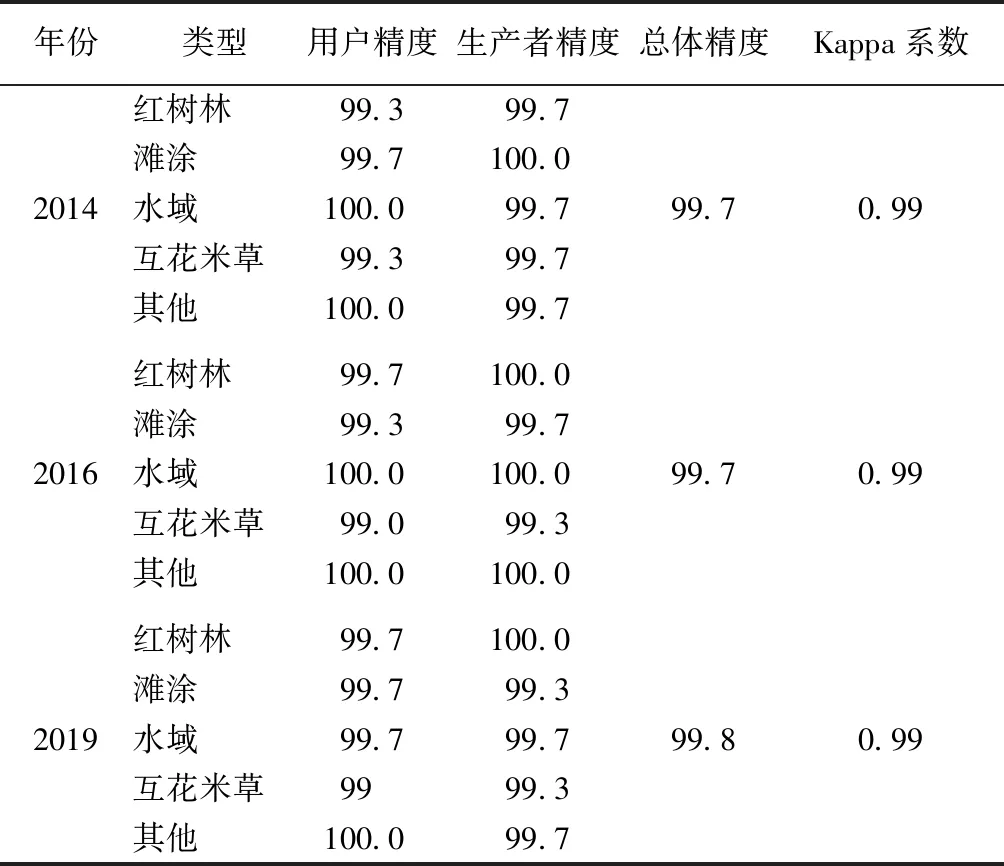
表1 精度评价报告

2014年、2016年和2019年泉州湾保护区各类型土地利用的分类如图1所示。

从表1中可以发现分类精度均超过95%,满足后续的研究基础。从图1中可以明显的发现,1,2,3处有明显的土地利用变化,其中：1处2014年是水域(主要是鱼塘)到2019年则完全转化为互花米草和滩涂；2处在2014年是其他类型到2019年大部分转变为红树林和滩涂；3处的互花米草在2014—2019年中逐渐减少,转而成为红树林；4处的水域在2014—2019年中逐渐转化为互花米草、滩涂和红树林；5处的其他类型则在2014—2019年中很大一部分逐渐被红树林取代。

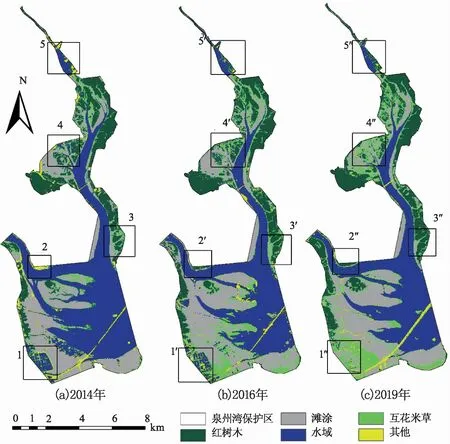
图1 泉州湾保护区影像分类结果

3.2 综合效益模型与计算结果

经过因子的权重计算最终得到综合效益模型公式如下:

Pa=0.368LuccE+0.211NDVI+0.101NPP(S)+0.085WP+0.077FS+0.061GDP+0.055FPV+0.042ETP

(6)

式中:LuccE为土地利用评分；NDVI为归一化植被指数；NPP(S)为植被净第一性生产力；WP为水质污染指数；FS为森林固定CO2能力；GDP为国内生产总值；FPV为食物生产价值,ETP为娱乐文化价值。

由以上模型分析得到2014，2016，2019年泉州湾保护区的综合效益,以2014年综合效益为基础,统计结果如表2所示。

将泉州湾保护区综合效益结果按自然分段法分为好、中、差个等级,最终得到图2。

表2 泉州湾保护区综合效益比值统计结果

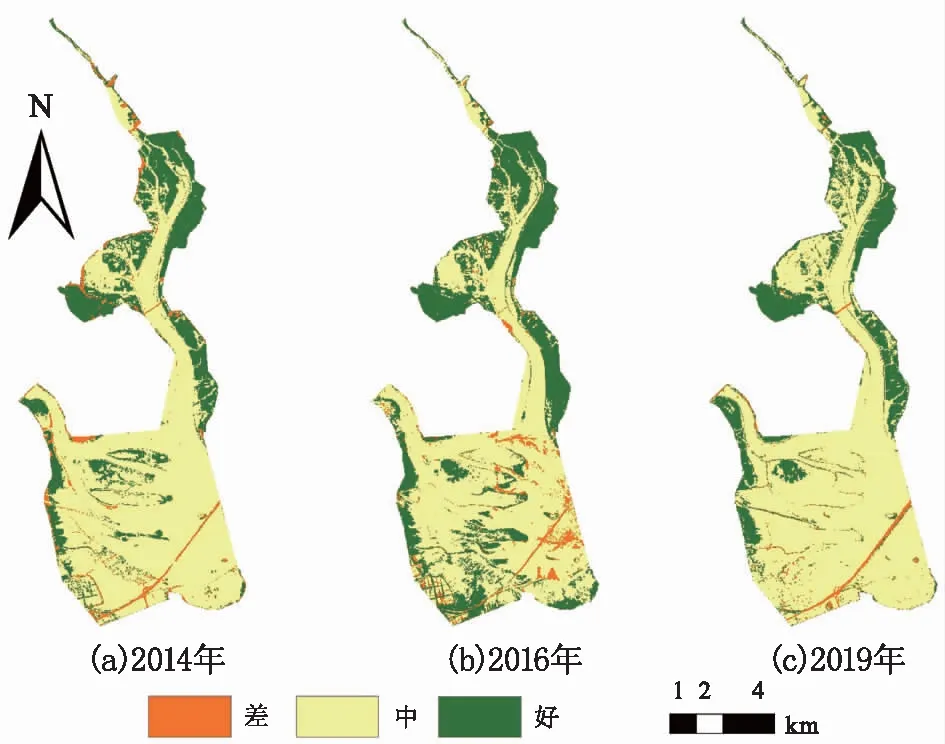
图2 泉州湾保护区综合效益分类图

由表2可以了解到:2014年泉州湾保护区的综合效益最低,2019年最高,相较于2014年增长了26%；2016—2019年综合效益增长速度最快,由2016年的1.08增长至1.26,2016—2019年综合效益增长16.7%；2014—2016年的年均增长率为4%；2016—2019年的年均增长率为5.6%。空间上,结合图2可以发现:综合效益较好的区域主要分布在水域较为狭窄的入海口处,而综合效益较差的地区主要在入海口处；与影像分类比较可知综合效益高的主要是红树林和互花米草分布的区域,而综合效益较差的地区主要的其他类型的区域。同样，从图中可以发现,虽然2019年泉州湾保护区综合效益是3期中最高,但综合效益为好的面积却不如2016年。

3.3 热点分析

空间自相关的分析显示(表3),综合效益的分布的聚集程度呈现先上升(2014—2016)后下降(2016—2019),总体呈略微上升趋势(2014年为0.445,2019年为0.472)

表3 Moran I分析结果

从表4中可以发现,3期中的热点区域中,红树林和互花米草占据了主要的份额,其中2014年占89.64%,2016年为95.07%,2019年为95.72%；其中红树林占比最高,2014年为78.2%,2016年为80.2%,2019年为82.64%。冷点区域中水域和其他类型占据了主要的份额,其中2014年为97.72%,2016年为96.38%,2019年为97.27%；其中水域占比最高,2014年为84.34%,2016年为79.36%,2019年为89.37%。而滩涂区域不论是在冷点区域还是热点区域都不足10%。

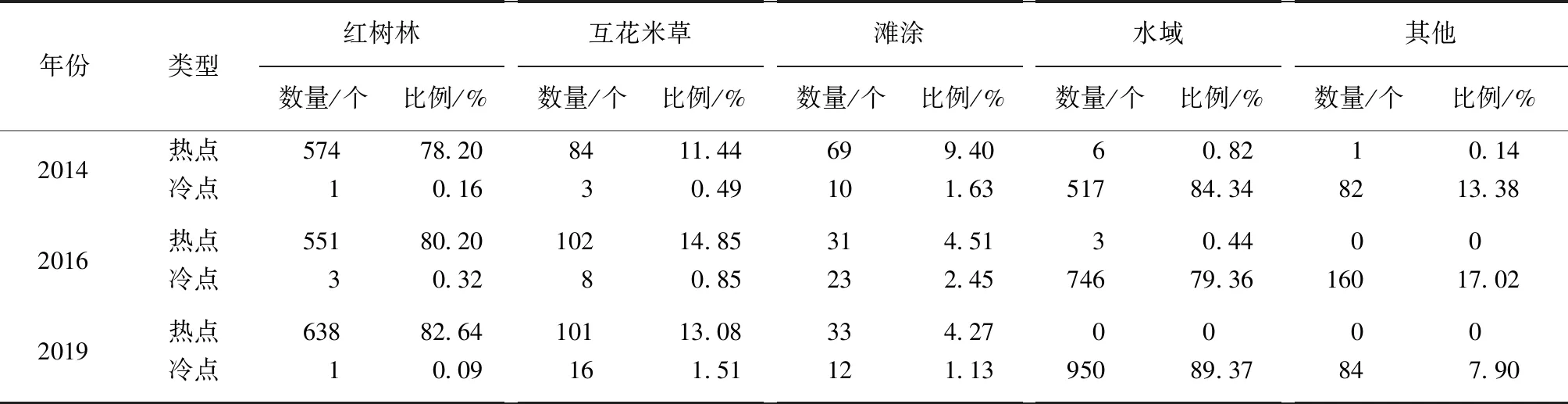
表4 冷热点数量(比例)统计结果

4 结论与讨论

综合效益随着时间的变化应该是动态变化的,结合遥感、地理信息、数据收集等多种数据源和方法,经过数据处理和因子计算,利用无量纲的一阶线性模型构建泉州湾保护区综合生态效益模型,根据模型计算2014，2016，2019年泉州湾保护区综合效益,同时将综合效益映射在空间上,完善在动态分析的层面上对泉州湾保护区综合效益的探讨。

4.1 综合效益结果讨论

1) 经过泉州湾综合效益模型的计算,结果显示2014—2019年期间,泉州湾保护区综合效益增长了26%,其中2016—2019年较2014—2016年的综合效益增长更为明显,由2014—2016年的年均增长4%,提升到2016—2019年的5.6%。结合泉州市年鉴与相关因子分析,2014年以来的综合效益增长与地区环保政策的加强、红树林湿地保护力度增加、整体GDP提升关系密切,而2016年后增速加快,主要原因与泉州湾大桥建设通车、环保督查政策、红树林湿地恢复等措施的实施较为紧密,从遥感影像中也能明显发现泉州湾大桥在2014年还处于施工阶段,而2016年则基本完成；2014年和2016年中多处鱼塘也在2019年时基本消失。

2) 通过泉州湾综合效益计算和综合效益图的绘制,虽然2019年的综合效益最高,但分类为好的分布面积明显不如2016年,其本质原因是:2019年归类为好的分布区中,其综合效益总和明显大于2016年,说明2019年时综合效益为好的区块含金量更高,效益更明显。结合实地调查和数据分析可以发现,这些地区的红树林长势更为成熟,红树林湿地的生态条件更好,由此显著提升效益值,同时结合热点结果分析,红树林区域的热点比例占据主要,其中红树林与互花米草区域的热点比例超过90%,而且2014—2019年,红树林区域内的热点逐渐上升,也能在一定程度上说明红树林区域在泉州湾保护区综合效益的计算中占很重要的地位,从侧面说明红树林和红树林湿地的保护工作十分重要且必要。

3) 红树林面积、红树林湿地的成熟情况能很显著地影响泉州湾保护区的综合效益,但并不意味着滩涂、水域、其他类型在实际的建设和保护过程中毫无必要,原因在于:本研究着重于泉州湾保护区的综合效益研究,并不着重于海洋或其他类型的综合效益计算,所以在因子选取的过程中着重选取相关因子；同时，由于条件限制,部分因子和数据的空间分布数量较少、均匀度不足,最终导致计算结果和热点分析后,综合效益的冷点主要分布在水域上。

4.2 不足与展望

泉州湾综合效益模型的建立和计算过程中,为追求动态效益的模拟,选取了多个时间点的数据,例如，遥感影像和水质污染,但在泉州湾这种河口、海口区域,不论是影像或者是水质,数值都随着每天潮汐、季节逐渐变化,而本次研究所选取的数据的代表性存在一定局限。为弥补这类局限带来的影响,引入无量纲的一阶线性模型,其中无量纲化能减少由于因子不足或者因子之间差异过大而带来的影响，但同时又引入计算结果无法数值化的问题。尽管如此,泉州湾保护区综合效益模型依然能有效的模拟时间上效益的趋势,空间上效益的分布。

为解决因子时间连续性不足,无量纲模型无法数值化的问题,后续研究将就这类问题提出解决方案。例如，通过引入更丰富的数据弥补,并结合市场价值法、替代价值法及机会成本法计算综合效益具体数值,从而将模型应用化,最终能更方便地为政策制定、细致化管理提供有效的依据。