模块化直流电源方案与控制系统设计

刘楚晖，楼伯良

（1.南京南瑞继保电气有限公司，南京 211102；2.国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

110 V/220 V 直流电源在发电厂、变电站中应用广泛，电源的稳定性和可靠性影响发电、配电的安全[1]。传统的直流电源多采用不控整流或者相控整流并辅以工频变压器进行输入、输出隔离，但是随着负载容量需求的提升，使得基于此种方案的直流电源工频变压器体积庞大、谐波污染大、功率因数低的问题越发明显[2-3]。随着全控电力电子器件的发展，基于IGBT 或MOSFET 的各种交直流开关电源应运而生[4-5]。对于中、大功率的直流电源，部分传统的开关电源拓扑不再适用，同时考虑单一电力电子器件的载流能力，使用单电源模块实现大电流输出并不现实，所以模块化并联成为主流的电力电子直流电源功率拓展思路[6]。对于由电力电子变换器级联构成的分布式电源系统，控制系统建模和稳定性分析是决定直流电源运行特性的先决条件[7-12]。其中，文献[7]建立CCM（连续导通模式）下Buck 变换器的输出阻抗模型并讨论输入电压、输出电流、穿越频率和滤波器参数对阻抗的影响。文献[8]建立移相全桥变换器的小信号模型并讨论功率等级、开关频率和控制方式对输出阻抗的影响。文献[9]建立同步整流Buck 变换器输入阻抗模型并验证其随功率等级、开关频率和控制方式变化的规律。

综上，本文首先提出一种基于模块化思路的直流电源方案，然后在确定变换器拓扑的基础上，对于多模块并联后的系统稳定性，从阻抗角度建立数字控制下系统频域模型并定量分析，最终研制出六模块并联、总输出220 V/600 A 的工程样机，验证本方案的工程可行性。

1 模块化直流电源方案

模块化直流电源的功率单元使用前级AC/DC 子模块和后级DC/DC 子模块串联而成。前级子模块采用单电感滤波两电平PWM（脉冲宽度调制）整流器的拓扑，作用是将输入380 V AC 整流成700 V DC 供后级子模块使用。后级子模块采用文献[13]中提出的Tr-Lag-TC 型移相全桥拓扑进行隔离降压输出，此种拓扑通过隔直电容避免高频变压器偏磁，并且通过在超前臂谐振电感的一端并联钳位二极管，减小由于高频变压器副边大容量整流二极管给电容充放电而对原边造成过大的电压振荡和尖峰。具体的功率单元拓扑如图1 所示。

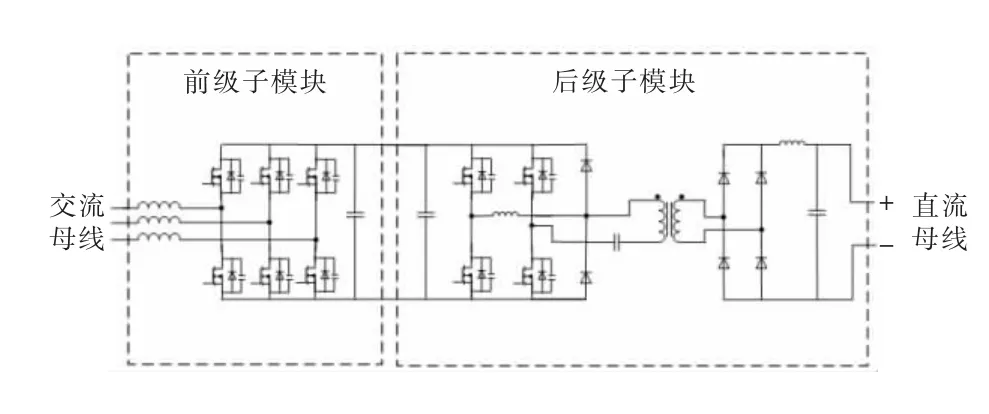
图1 功率单元拓扑

前级子模块与后级子模块的全控功率器件均使用碳化硅MOSFET，开关频率与控制频率为48 kHz，通过高频化减小交流侧滤波电感、高频变压器、谐振电感和直流滤波电感等核心无源器件的体积，从而将单个子模块体积控制在3U 标准机箱的范围内。

多个功率单元在交流输入侧和直流输出侧直接并联，可迅速实现直流电源功率等级的提升。

2 前级子模块控制系统分析

2.1 前级子模块电流环及输入阻抗模型

图2 所示为前级子模块电流环控制框图。图中Iref（s）为电流环指令，Gi（s）为电流环PR（比例谐振）调节器，Gd（s）为控制系统延时，KPWM为PWM 整流器电压放大倍数，L 为交流滤波电感感值，Lg为电网阻抗感值，Ug（s）为电网电压，Hv（s）为网侧电压前馈环节传递函数，Hi为网侧电流反馈系数。

图2 前级子模块电流环控制框图

化简该控制框图可以得到控制到输出的传递函数为：

式中：Zg（s）=sLg为电网阻抗；T（s）和Zi（s）分别为电流环开环传递函数和PWM 整流器的输入阻抗。

2.2 多模块并联时控制系统模型简化

对单个前级子模块使用诺顿等效电路构建如图3 所示的多模块并联时的等效电路。

考虑到所有子模块控制参数和硬件参数基本一致，故采取Zi1（s）=Zi2（s）=…=ZiN（s）=Zi（s）进行简化。根据电路理论叠加定理，总电网输出电流ig（s）和流入第k 台前级子模块的电流igk（s）为：

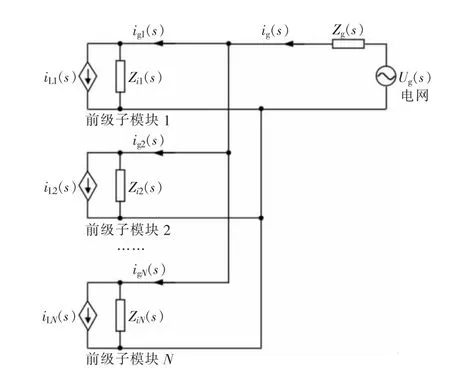
图3 多前级子模块并联时的等效电路

由上述两式可以看出，N 个前级子模块并联后，整个控制系统保持稳定的充要条件可简化为：

（1）电流环在电网阻抗为0 时，即完全理想电网时保持稳定。

（2）电流环在电网阻抗为NZg（s）时保持稳定。

2.3 理想电网下的电流环稳定性

数字控制系统延时由两部分组成[14-15]：一部分为PWM 调制固有的0.5Ts延时（Ts为数字控制周期）；另一部分为数字控制系统计算延时，具体为采样时刻和底层脉冲发生器刷新PWM 占空比时刻之间的时间，用λTs表示。为了避免在触发采样时采集到功率器件开关过程的振荡且为了避免调制波和载波在一个开关周期内多次交截，通常在对称三角载波的谷值或峰值处触发采样和刷新PWM 占空比。所以在开关频率与控制频率相同的前提下，考虑数模转换器延时和实际程序执行时间，最小数字控制系统计算延时为0.5Ts，即λ=0.5。当开关频率较高时，受芯片计算速度和模数转换器转换速度所限，λ 会不可避免地变大，成为1.0，1.5 等等。为了不失一般性，总数字控制系统延时Td=（λ+0.5）Ts，其传递函数为：

令式（2）中Lg=0，得到理想电网情况下电流环开环传递函数为：

电流环PR 调节器在基波50 Hz 处存在+90°到-90°的相位突变，在中高频段相位滞后可近似为零，所以随着信号频率升高，电流环开环传递函数相位受Gd（s）的影响逐渐下降，穿越频率fx根据式（8）近似计算：

式中：fs为数字控制周期，满足fs=1/Ts。

由式（8）可以看出，对于理想的模拟控制系统，令λ=0，穿越频率为fs/2，可以达到采样定理限制的最大值。而对于实际的数字控制系统，随着数字控制系统计算延时的增大，电流环的穿越频率越来越低，这严重限制了系统的响应速度。

忽略中高频段PR 调节器谐振项的影响，电流环GM（幅值裕度）的表达式近似如式（9）所示，其中kp为PR 调节器比例系数

根据式（9）可以看出，前级模块的功率等级、电压等级、硬件参数、控制频率、开关频率和数字控制系统延时都确定后，提升电流环幅值裕度的有效方法是减小PR 调节器的比例系数。

2.4 弱电网下的电流环稳定性

2.4.1 稳定性判据

根据2.2 小节的电路模型分析，随着并联的前级模块数增加，单模块面对的等效电网阻抗NZg（s）成比例增大。文献[16]中提出一种针对分布式电源系统基于源荷阻抗比的稳定性评判方法，可行的阻抗比范围如式（10）所示：

式中：Zo（s）为电源的输出阻抗；Zi为负载的输入阻抗。该判据可以确保源荷级联系统的稳定性以及Zo（s）/Zi（s）具有6 dB 的幅值裕度和60°的相位裕度。

对于模块化电源系统，上述判据中电源输出阻抗即为N 倍的电网阻抗，而负载输入阻抗即为单个前级模块的输入阻抗。

图4 为并联模块数分别为1，2，3 时的阻抗比奈奎斯特图，电网阻抗Lg=30 μH，滤波电感L=100 μH。随着并联前级模块数的增加，阻抗比的实部越来越接近-1/2，整个系统存在不稳定的风险。

图4 并联模块数目变化时的阻抗比奈奎斯特图

2.4.2 提升弱电网适应性的方法

为了在并联模块数增加时确保控制系统的稳定性，可以采取增加前级子模块内部交流滤波电感值或网侧电压前馈环节进行低通滤波两种方法。

图5 为增加滤波电感感值后的阻抗比奈奎斯特图。电网阻抗Lg=30 μH×3=90 μH，为了保持理想电网下电流环幅值裕度不变，PR 调节器的比例系数kp也按照滤波电感数值同比例放大。可以看出，增大交流电感感量可以使阻抗比实部远离-1/2，从而有效提升控制系统稳定裕度，但是会造成电感成本与体积的上升。

图5 交流滤波电感数值变化时的阻抗比奈奎斯特图

图6 为网侧电压前馈环节采用一阶低通滤波后的阻抗比奈奎斯特图。低通滤波器时间常数为Tf=5 ms，电网阻抗Lg=30 μH×3=90 μH，滤波电感L=100 μH。此方法同样可以有效提升控制系统的稳定裕度，但是牺牲了前级子模块输入阻抗的幅值，在电网电压谐波含量较高时，并网电流谐波含量也会增大。

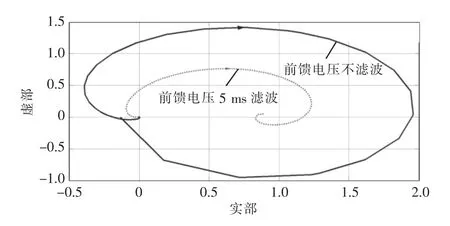
图6 网侧前馈电压低通滤波后的阻抗比奈奎斯特图

2.5 仿真验证

2.5.1 仿真参数

在MATLAB/Simulink 环境下搭建多前级子模块并联的仿真模型，仿真参数如下。

开关频率、控制频率均为fs=48 kHz，额定功率Sb=30 kW，额定电压Ub=380 V，PR 调节器比例系数kp=0.5，PR 调节器谐振系数kr=80，PWM整流器电压放大倍数KPWM=537.3，网侧电流反馈系数Hi=0.015 5，电网阻抗Lg=30 μH，数字控制系统计算延时λTs=1Ts=1/fs。

2.5.2 仿真结果

在单一地改变滤波电感L、网侧电压前馈环节传递函数Hv（s）、并联子模块数N 的情况下进行仿真，图7 为各种工况下的单模块三相电流波形。

图7 不同工况下的仿真结果

从图7（a）和图7（b）可以看出，并联子模块数从3 增加到4 后，子模块的交流电流已经失控变得过大。由图7（c）和图7（d）可知，增加滤波电感值或网侧电压前馈增加低通滤波均可以使电流稳定，但是前馈电压增加低通滤波会导致子模块输入阻抗幅值减小，从而增大电流的谐波含量。

3 后级子模块控制系统分析

后级子模块采取图8 所示的电压-电流双闭环的控制架构，同时进行负载电流前馈以提高电源系统对变化负载的响应速度。

为求取后级子模块的输出阻抗Zob（s），令Uref（s）=0，同时令ZL（s）=1/[s（Lo+Lr/K2）]，ZC（s）=1/s/C，画出控制框图对应的信号流，其中：Io（s）为输入节点，Uo（s）为输出节点，如图9 所示。

图8 后级子模块控制框图

回路有3 条，增益分别为L1，L2，L3：

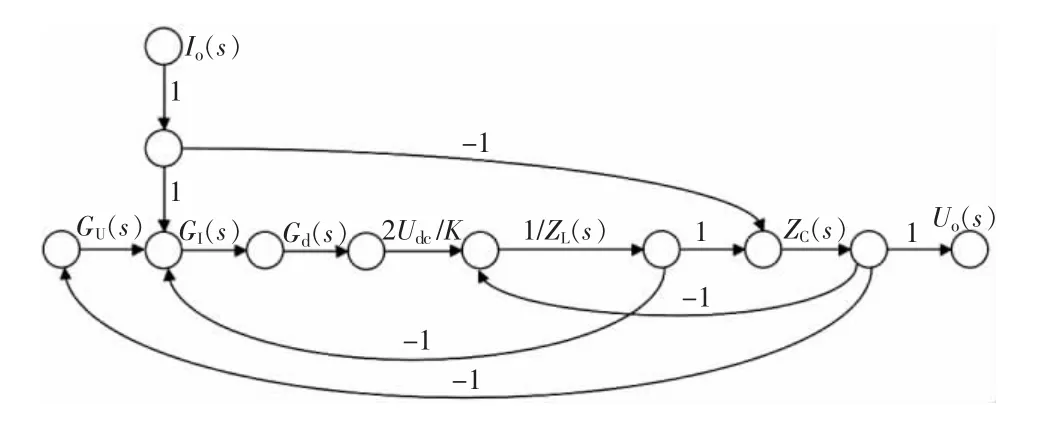
图9 信号流

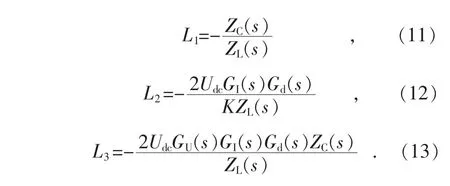
无互不接触回路，所以特征式Δ 为：

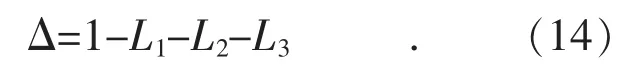
前向通路2 条，增益分别为P1，P2，对应的余子式分别为Δ1，Δ2：

综上，可以得到输出阻抗Zob（s）的表达式为：

以下参数为例画出输出阻抗波特图，开关频率、控制频率均为fs=48 kHz，kp_U=0.001 7，ki_U=3.646，kp_I=1.5，ki_I=0.3，Udc=700 V，K=2，Lo=40 μH，C=125 μF，Lr=10 μH，数字控制系统计算延时λTs=1Ts=1/fs。

从图10 可以看出在中低频段控制器的带宽内，输出阻抗幅值很小并呈现电感特性，随着频率上升，超出控制器带宽，输出阻抗幅值逐渐增大并在某一频率点达到最大幅值。如果后级子模块所接的负载在此频率附近的输入阻抗幅值和相位不满足式（10），则整个电源负载级联系统有不稳定的可能。在高频段，输出阻抗幅值逐渐减小并呈现电容特性。

图10 输出阻抗波特图

4 工程样机

基于上述理论分析，研制了一台额定交流输入电压380 V、额定直流输出电压220 V、额定直流输出电流600 A 的直流电源柜，见图11、图12。整柜采取六功率单元并联的方案，共六个前级子模块和六个后级子模块。

图11 工程样机正面外观

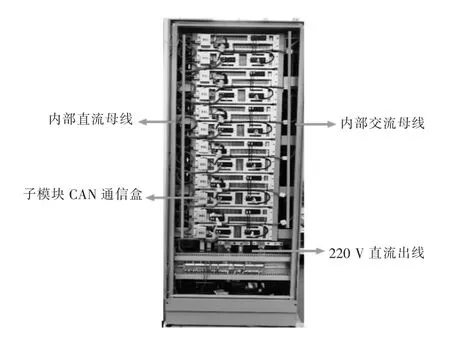
图12 工程样机背面外观

功率实验时用一台1 MW 的集中式逆变器作为电源柜的负载，总负载电流设定为600 A。图13 为整柜运行时的示波器波形截图和总交流输入线电流的谐波分析结果，采样通道1 为单功率单元的直流输出电流（50 A/格），采样通道2 为直流输出电压（100 V/格），采样通道3 为总交流输入线电流（100 A/格），采样通道4 为交流输入线电压（500 V/格）。

受模组尺寸所限，前级子模组的粉芯交流滤波电感值在100～200 μH，空载时电感值较大，随着电流上升电感值变小，为了保证并联系统的稳定性，实际采取上文提到的前馈电压进行低通滤波的方案，但对实际电网电压背景谐波抑制能力减弱，导致5，7，13 等低次谐波含量明显。

图13 示波器波形

5 结语

本文提出一种模块化直流电源方案，单功率单元使用前级AC/DC 子模块和后级DC/DC 子模块串联而成。前级子模块采用单电感滤波两电平PWM 整流器的拓扑，后级子模块采用移相全桥拓扑。

对于前级子模块，推导单前级子模块电流环、输入阻抗模型和多模块并联时的等效电路，指出多模块并联时为确保系统稳定性需同时满足以下两个条件：

（1）电流环在电网阻抗为0 时，即完全理想电网时保持稳定，通过减小PR 调节器比例系数可以提升稳定裕度。

（2）电流环在电网阻抗为NZg（s）时保持稳定，通过增大滤波电感数值或网侧电压前馈进行低通滤波可以提升稳定裕度。

对于后级子模块，根据电压电流双环控制框图化简并推导输出阻抗表达式，分析各频段内的输出阻抗特点，为确立此直流电源可带负载阻抗的范围提供理论依据。

最后基于上述分析，研制了1 台输出220 V/600 A 的六功率单元并联电源样机，验证了本文模块化电源方案的可行性。