基于傅里叶变换和倒谱系数的电子音乐标记算法

范勇冠

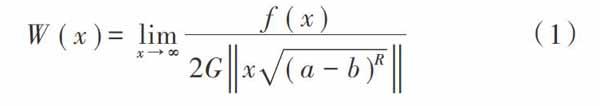
摘  要： 为解决当前对电子音乐标记准确性差、分辨率低的问题，提出基于傅里叶变换和倒谱系数的电子音乐标记算法。首先结合傅里叶变换算法采集电子音乐的特征频谱，并进行特征信号的分辨，以此计算出电子音乐的倒谱系数，根据匹配后的倒谱系数对电子音乐进行高精度分辨处理，根据分辨结果实现对电子音乐特征数值的准确标记。最后通过实验证实，基于傅里叶变换和倒谱系数的电子音乐标记算法相对于传统方法具有更高的准确性和分辨率，充分满足研究要求。

关键词： 傅里叶变换; 倒谱系数; 电子音乐; 音乐速度; 节拍; 谱图

中图分类号： TN911.1?34; TP393                   文献标识码： A                    文章编号： 1004?373X（2020）13?0155?04

Electronic music marking algorithm based on Fourier transform and cepstrum coefficient

FAN Yongguan

（Jiangxi University of Technology， Nanchang 330098， China）

Abstract： In view of the poor accuracy and low resolution of current electronic music marking， an electronic music marking algorithm based on Fourier transform and cepstrum coefficient is proposed. The characteristic spectrum of electronic music is collected by taking into account the Fourier transform algorithm， and the characteristic signal is distinguished to calculate the cepstrum coefficient of electronic music. According to the matched cepstrum coefficient， the electronic music is subjected to high?precision resolution processing， and the electronic music characteristic number is accurately marked according to the resolution result. In the end， the experiment proves that the electronic music marking algorithm based on Fourier transform and cepstrum coefficient has higher accuracy and resolution than the traditional method， which fully meets the research requirements.

Keywords： Fourier transform; cepstrum coefficient; electronic music; music speed; beat; spectrum diagram

0  引  言

目前，電子音乐愈来愈流行，快速对电子音乐的倒谱系数特征进行采集可更好地实现对音乐信息的搜索。因此，对电子音乐特征进行标记也逐渐成为当前相关企业研究的重要内容之一，而电子音乐标记特征的采集和搜索过程中一个重要的属性特征就是进行音乐信息倒谱系数算法研究。电子音乐倒谱系数已经渗透到预估电子音乐速度、掌握准确节奏、锁定音乐节拍等领域[1]。基于傅里叶变换和倒谱系数提出了一种新模式电子音乐信息标记算法，以电子音乐倒谱系数和速度特征为原始粒子建立特征频谱，汇总出多余的电子音乐特征数值模型，再以算法跟踪的原理计算电子音乐倒谱系数，形成总特征频谱[2]。与传统的函数计算、运用傅里叶的算法比较发现，基于傅里叶变换和倒谱系数的电子音乐标记算法具有更高的音乐特征信息分辨率和完成度。

1  电子音乐标记算法

1.1  电子音乐特征标记

电子音乐信息频谱的作用就是在原始的音符中测定函数特征图形，从而判断音乐的周期特点。根据测定函数特征[a]和原始延迟特征[b]的差异或者相似度来提取电子音乐的特征函数周期[R]，并结合傅里叶变换算法测定电子音乐的自身频率[Z]，对音乐的特征函数[G]和被限定频率[f（x）]进行正交基处理，从而判断其相似程度，并把相似度图形划分为有规律延迟特性的原始曲线，以便提高音乐特征的分辨率[3]。在此基础上对电子音乐分辨率的特征数值进行计算，具体算法如下：

基于上述算法进一步进行电子音乐特征的处理。考虑到相似音乐的匹配完整度，为了避免匹配误差，对电子音乐信息频谱自身局限特征进行判别，在判别过程中，音乐特征信息速度变化越快则特征数值系数越高，其音乐分量也相对越少，稀疏度就越好[4]。不规定电子音乐特征频谱的形式和数量，则这一时刻的音乐定位速度就越准确，频谱的使用性就得到保证。为解决传统的电子音乐信息频谱有缺陷、不完整的问题[5]，基于傅里叶变换算法对原始音乐[a（n）]里的音符先进行添窗，记为[w（n）]，然后再进行自身特征运算，利用时间延迟数值[m]来获得原始音符的周期特点，将延迟变作电子音乐信息的速度度量，最后构成最终的音乐特征频谱，其计算公式为：

式中：[t]是电子音乐发生离散的时间;[x]表示电子音乐中的原始音符点;[y]表示电子音乐的特征测定点。

若音乐特征函数的中间点[w（n+x，m+y）]是支撑着的方形窗[6]，若[S]是对电子音乐特征的抽样频次，则时间延迟[I]对应的周期就是[IS]，发生频次为[U]，所对应的速度是[t1=60IS]，这样分别求出频率的属性特点，从而求出电子音乐信息频谱，计算公式如下：

根据傅里叶离散变换法，将[w>0]离散化的间隔频点记为[f（SN）] Hz;若电子音乐特征频率的范围为[k]，则对电子音乐特征数值进行计算，具体算法为：

基于上述算法实现对电子音乐倒谱系数特征的采集和标记，以便后续进行音乐特征的精准分类和准确分辨[7]。

1.2  电子音乐特征信号分辨

根据分类识别算法对电子音乐的不同分类属性特征进行识别，生成电子音乐信息特征频谱，测定函数原始点的电子音乐音符，逐个分析测定函数以后再对得到的每一个都分别进行追踪匹配分析，最后按照前文得到的特征数值分析系数来计算生成电子音乐信息速度频谱[8]。详细的电子音乐特征信号分辨步骤如下：

1） 预先加重处理。电子音乐信息特征信号的高频部分的能量通常会出现不足的现象，要根据傅里叶变换和滤波变换原理对干扰的低频数值进行消除过滤，从而更容易获得高频频谱，这个过程就是预先加重处理，具体的算法为：

2） 电子音乐信号峰值添窗。电子音乐信号通常会出现一些峰值和频率较高的信号，这些不够平稳的信号非常难处理，需要对分页信号进行进一步添窗使得信号变得平稳[9]。电子音乐信号峰添窗的信号算法为：

一般遇到的添窗函数主要是海明窗，对海明窗进行计算处理，其函数为：

3） 测定静音页。这是由于电子音乐信息速度的信号中总会出现没有音乐信号属性特征的静音页，这会大大影响实验的结果[10]。因此需要设定音乐频率的短能量阈值来测定静音页，如果说能量比阈值低，就需要把此能量消除，因此将阈值设定为0.1。

具体的电子音乐特征信号分辨步骤如图1所示。

为保障特征信号分辨结果有效，进一步提取电子音乐中的MFCC的属性特征。MFCC属性特征是在平时的音乐课程任务中很常用的特征之一，假设人类的耳蜗是一组滤波器[11]，根据音乐不同频率的过滤消除和带宽属性来完成对各种声音的分辨，MFCC就是这种能力的体现，具体的电子音乐速度信号的频率与梅尔倒谱系数的关系如下所示：

从式（8）中可得，若声音的信号频率低于1 000 Hz，梅尔滤波就呈线性相关的关系;若声音的信号频率高于1 000 Hz，梅尔滤波就呈对数的关系。通过对声音信号预先加重处理之后，初步进行快速傅里叶变换得到各页声音信号的频谱数据信息，再通过计算平均方法计算每一页的频率功率频谱并设计一个梅尔滤波进行原始的频谱过滤，从而计算出每一个滤波输出的线性相关和对数能量[12]。最后对输出的有效结果变换离散余弦就可以得到电子音乐特征信号分辨特征属性数值，进一步实现对子音乐特征的标记处理。

1.3  电子音乐标记的实现

基于上述算法进一步对电子音乐特征进行标记。利用最常用的电子音乐信息速度的区间[D∈][30，600]，把区间按一定的电子音乐信息速度识别率的要求将速度集合变成频率集合[13]。对频率集合中的每一个频率都建立原始原子，再按一定的颗粒度对全部原始原子进行右移位的操作，一个原子的生成对应一个步骤的移动，最后全部的移动生成原子加上原始原子组成了原始原子频率集合。把頻率集合中的所有频率对应的原子[d]组成冗余复杂字典[D]，再建立一个[p×q]的方形矩阵，音乐个数是[p]，音乐属性特征用[q]表示，具体的矩阵如下：

基于式（10）进一步进行计算，若TOPK属于电子音乐[f]，[g]的共同特征属性集合，[efg]表示电子音乐1包含的特征属性，[en]表示电子音乐相似特征属性[14]，根据对电子音乐特征矩阵的预测评分来预估用户对电子音乐的评价，计算各种音乐的相似程度并进行标记，其具体的特征相似度属性预估评分算法如下：

若rateItems表示电子音乐的特征集合;[u]表示电子音乐获取的平均标记得分;[rfg]表示用户对电子音乐的评分;[c]表示标记数量。进一步进行电子音乐相似度预测评分的标记处理，具体的计算方法为：

基于上述算法对得到的电子音乐特征训练信息数据进行维度的降低处理和训练，并对处理结果进行标记，实现电子音乐特征数据的信息学习[15]。通过Softmax函数分类法进行分析处理，这样就完成了分类，具体根据DBN进行电子音乐信息情绪分类架构，如图2所示。

在完成了电子音乐标记流程之后，就可以初步实现傅里叶变换和系数倒谱的电子音乐速度标记算法的优化，生成更加准确的电子音乐信息速度频谱，从而达到更高的电子音乐信息速度识别率，较现有的传统算法具有更好的稀疏力。

2  仿真实验

2.1  实验环境及参数

为验证基于傅里叶变换和倒谱系数的电子音乐标记算法的准确性和有效性，与传统方法进行对比检测，并记录检测结果。为保障检测结果的有效性，对实验检测环境和参数进行统一设计。实验环境结合BP神经网络和PC机原理进行设置，CPU选择Intel Xn E8?1210v4系统，四核心八线，主频2.7 GHz Windows 10操作系统，Matlab 7.6实验平台。应用基于Java语言的Web平台。

2.2  实验结果分析

在上述实验环境下进行对比检测。为方便记录，在音频特征相同的情况下，将传统算法检测结果记为曲线B，本文算法记为曲线A。具体对比实验检测结果如图3所示。

在上述实验检测过程中，电子音乐分辨率检测相邻点间隔越小，说明其标记的准确度越高。观察图3可知，曲线A的相邻节点数值明显相对于曲线B更加紧密。进一步观察两组检测曲线的分辨率数值发现，相对于曲线B而言，曲线A的分辨率明显更高，可达到90%，证实基于傅里叶变换和倒谱系数的电子音乐标记算法的有效性相对更佳。基于上述检测结果可知，基于傅里叶变换和倒谱系数的电子音乐标记算法相对于传统算法而言，有更高的实用性和标记准确性。

3  结  语

本文提出一种基于匹配追踪的电子音乐速度谱图生成算法，该算法比自相关函数法和傅里叶变换法具有更高的电子音乐分辨率，在应用时可更准确地对电子音乐特征进行标记，这对电子音乐的发展具有重要意义。

参考文献

[1] 李杰，孙奇，陈爱玲，等.基于Unity3D的音樂交互游戏设计与实现[J].现代计算机，2017（13）：62?65.

[2] 王诗俊，陈宁.基于混合判别受限波兹曼机的音乐自动标注算法[J].华东理工大学学报（自然科学版），2017，43（4）：540?545.

[3] 徐宏伟，严迪群，阳帆，等.基于卷积神经网络的电子变调语音检测算法[J].电信科学，2018，34（2）：46?57.

[4] 葛芳辛，贾丽梦.浅析钢琴演奏中影响力度呈现的因素[J].艺术科技，2017，30（7）：171?172.

[5] 毋亚男，刘德然，许小可.基于双向情感分析的实时性音乐推荐系统设计[J].大连民族大学学报，2017，19（1）：76?79.

[6] 张景扩，彭龑.一种基于倒谱法的基音周期检测改进算法[J].电声技术，2017，41（7）：113?116.

[7] 林朗，王让定，严迪群，等.基于修正倒谱特征的回放语音检测算法[J].计算机应用，2018，38（6）：1648?1652.

[8] 陈锦飞，徐欣.基于梅尔频率倒谱系数与动态时间规整的安卓声纹解锁系统[J].计算机工程，2017，43（2）：201?205.

[9] 罗彧.钢琴教学中的“分句”教学：影响乐句划分的因素及教学要求[J].北方音乐，2017，37（7）：151?156.

[10] 桂文明，刘睿凡，陶玉婷，等.一种新型音乐速度谱图的生成算法[J].复旦学报（自然科学版），2018，57（3）：379?384.

[11] 李艳，李葆华，王金环.一种新的基于LDA?MURE模型的音乐个性化推荐算法[J].吉林大学学报（理学版），2017，55（2）：371?375.

[12] 刘莹，赵彤洲，邹冲，等.基于频谱包络分析的音乐推荐算法[J].软件导刊，2018，17（6）：74?76.

[13] 陈培培，邵曦.基于生成对抗网络的音乐标签自动标注[J].南京信息工程大学学报（自然科学版），2018，10（6）：754?759.

[14] 谭斌，孙界平，琚生根，等.基于状态转移的奖励值音乐推荐研究[J].四川大学学报（自然科学版），2018，55（4）：719?726.

[15] 薛亮，黄美帆.华语流行音乐的歌词情绪分析：基于新媒体音乐终端的大数据分析方法[J].音乐传播，2017（4）：77?81.