单元整理复习课究竟要给学生留下什么

鲁春梅 许华庚

【案例背景】

单元整理复习课是小学数学课堂教学中的重要课型之一，它不同于新授课和练习课。单元整理复习课的任务是针对某一阶段所学的知识进行归纳、整理，使之条理化、系统化，通过查缺补漏，进一步巩固基础知识、深化基本技能、提升学生学习和解决实际问题的能力。

2019年12月11日至13日，云南省“万人计划”小学数学许华庚名师工作坊分别在云南财经大学附属中学、龙泉育才学校、金实小学三地举行了以“单元整理复习研讨”为主题的线下研讨活动。本次活动从人教版上册二至六年级教材中分别选取了一至两个单元的整理复习内容进行3位坊员的同课异构，17人上了六个课题。因单元整理复习课是大家公认的难上之课，故在活动之前，坊主许华庚老师就针对这一主题为我们坊员进行了线上线下培训，我们认真研读许老师发出的学习资料，进行网络讨论，而后对自己执教的内容进行精心准备。

【案例描述】

在研讨活动之前，坊主许华庚老师分享了他自己撰写的学习资料《复习课应让学生经历“梳”与“理”，“练”与“思”的过程》。通过学习，我们认识到单元整理复习课应具备三大特点：一“梳”，对所学知识进行系统梳理，使之“竖成线，横成片”，达到提纲挈领的目的;二“理”，理清知识的来龙去脉，前因后果;三“练”与“思”，让学生在“练”与“思”的过程中做到触类旁通、举一反三。

3天的时间，17节课听下来，感触颇多。虽然每位坊员对所上的课都进行了精心准备，但是距离一节好的单元整理复习课还有很大差距。我们的17节课虽然都是单元整理复习，但却上出了不同的味道、较大的差距。有的上成了练习课，有的看上去像是单元整理复习课，却也只是进行简单的知识罗列，没有对知识体系进行构建，未能形成“竖成线，横成片”的知识网络体系。这3天的活动结束，让我们对单元整理复习课有了新的认识和进一步的思考：在教学单元整理复习课后，我们究竟该为学生留下什么呢？我想在这次坊主许华庚老师执教的“多边形的面积整理和复习”一课中，一定能找到答案。

【案例解决】

一、梳理基本图形阶段

1.回顾：你学过哪些平面图形？

2.构成这些平面图形基本要素是什么？

3.点、线、面之间，有怎样的联系？

许老师从“点—线—面—体”之间的联系谈起，很多的点构成了线，线能围成面，面又能围成体。

4.由基本图形组成的精美图形，是由哪些基本图形构成的？

接着让学生比赛说基本图形的公式，并用字母表示，然后再抢答几个基本图形的面积。

5.如果给这三个精美图形穿上外衣，会把穿上外衣的多边形分割成几个基本图形吗？

许老师通过把多边形分割成几个基本图形的活动，介绍了辅助线，帮助学生找到组合图形（多边形）与基本图形的联系。

二、梳理公式推导阶段

平行四边形、三角形、梯形的面积公式是用什么方法？怎样推导的？（提示：分割策略、补形策略、双拼策略、平移法、转化思想）

在梳理公式推导阶段，分别对平行四边形、三角形、梯形的面积推导过程进行了个体罗列，同时回顾了在推导过程中用到过的策略：平移法、补形法、双拼法、转化思想等数学思想方法，让学生充分体会到知识间的联系。

三、应用策略解决问题阶段

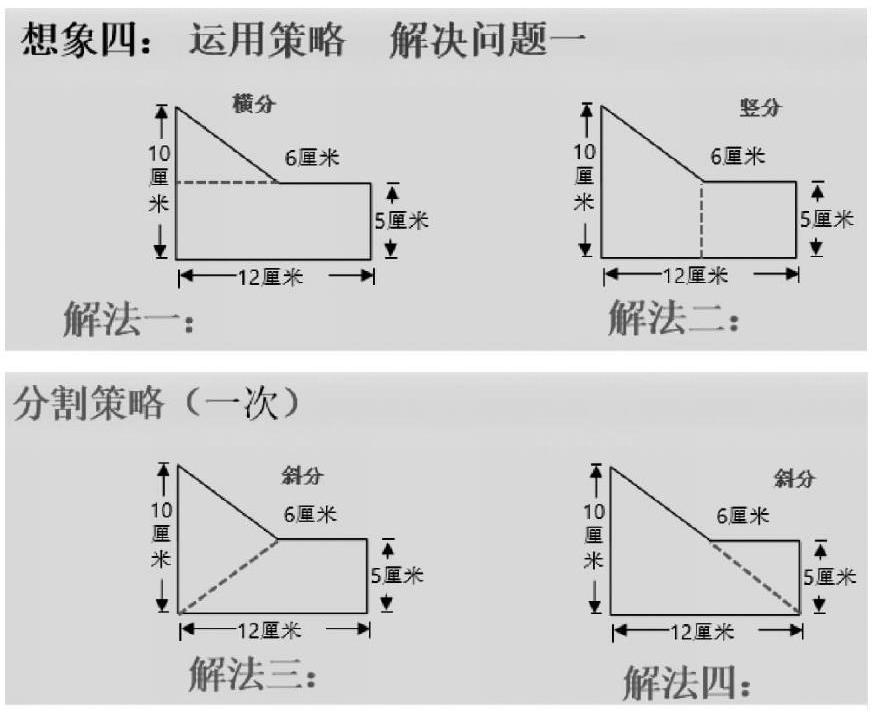
许老师围绕同一个组合图形，运用不同的策略解决求总面积的实际问题，从而来巩固基础图形的面积计算。在此过程中，许老师采用了分类的思想：

第一类是分割策略（强调分一次，多次分会使简单的问题变复杂）。

让学生说出各个图形是怎样列式的。

第二类：补形策略（3种不同的补形策略）。

让学生说出各个图形是怎样列式的。

许老師仅仅通过求一个组合图形的面积，既复习了组合图形的面积计算方法，又巩固了已学基本图形的面积计算公式，同时还锻炼了学生的思维，真是一举多得。

四、设置矛盾冲突，揭示知识本质阶段

让学生经历了一题多解之后，许老师让学生发现问题与提出问题，对解法四进行提问：这样的斜分策略你有什么需要提问的吗？

作辅助线进行分割的依据是什么？

许老师通过图形演示的方法引出对角线，并进行讲解说明。

五、应用对角线与对称轴知识本质解决阶段

接下来便利用对角的线或对称轴解决问题，出示教材第103页的思考题：一副七巧板拼成的正方形，边长4厘米，求每个图形的面积。

许老师在拓展提升阶段，让学生利用对称知识，采用双拼策略，求出各个组合图形的面积。

最后许老师说，把看不见的对称轴想象出来或画出来，就能帮助我们解决许多科技上的重要问题，于是出示图片：蝴蝶、飞机、少数民族头饰、建筑装饰……

许老师把课本上的知识和生活应用相结合，特别是用一架缺少另一半对称图形的飞机进行爆炸声的演示，起到了画龙点睛的作用，让学生更加深刻体会对称知识的重要性。这样不仅拓展了学生的视野与想象，更培养了学生的创造力与创造性思维。

六、形成单元整理复习知识网络阶段

许老师在最后全课小结时，当学生说完收获：三角形和梯形用双拼的方法转化成平行四边形来推导出了面积计算公式，平行四边形用分割、平移、补形等方法转化为长方形推导出了面积计算公式。随后用粉笔在黑板上潇洒一画，一棵大树豁然出现在了同学们的眼前，为同学们留下了清晰可见的知识网络体系。长方形是最基础的“根”，它犹如一棵大树的树干……

这样的一节单元整理复习课是非常成功的，在大容量的课堂中既有对知识的梳理、方法的提炼，更有通过一题多解所达到的“练”与“思”的思维拓展与提升。最后的板书更是这一节课知识网络最好的凝练，单元整理复习课结束后，相信这棵大树型的知识网络也一定会留在每一个学生的脑海中。

【案例反思】

1.单元整理复习的关键是在查缺补漏。

查缺补漏本身就是复习课的一大特点，单元整理复习课的关键也应该是准确找寻到学生的所缺所漏。许老师在课中强调三角形和梯形面积推导是采用双拼法，所以要除以2，这也是学生经常容易出错的地方。在平常教学中，我们应该多关注学生平时的课堂练习和家庭作业情况，弄清楚学生对哪些知识还处于模糊阶段，从而更准确地寻找遗漏，进而进行单元整理复习课的设计，相信这样的单元整理复习课才是真正适合学生的。

这应该是一节单元整理复习课后应该留给学生的——查缺补漏。

2.单元整理复习的保障是练习设计。

单元整理复习课确实是以练习为主线的，但是要侧重典型性、普遍性、综合性，要让学生在梳理的脉络中进行综合，在综合应用中强化“练”与“思”的過程，真正能够做到举一反三、触类旁通。本内容通过一道求组合图形面积的题，既复习了多边形基本图形面积公式，又复习了组合图形面积的计算方法，还发散并渗透了公式推导中的分割策略、补形策略。在求组合图形面积时，再次应用分割策略、补形策略来解决生活中的实际问题。不仅体现了学以致用的应用意识，还在巩固练习中渗透一题多解、一题多变的思想。在单元整理复习的练习中，要特别注意不应求全，应该求变，不能用习题的量来代替习题的质，不能以练习代替复习，更不能以机械性的题海战术代替学生的思维发展而扼杀了学生的创造性思维。

因此一节单元整理复习课也应该给学生留下：一题多解、一题多变，举一反三、触类旁通、学以致用。

3.单元整理复习的核心是梳理知识后形成的网络体系。

单元整理复习课并非一味地重复过去所学的知识，而是将独立分散的知识内容，特别是有内在联系的或有规律的知识内容，通过归纳整理的方式联系起来，使所学知识“纵成线”“横成片”，让知识更加系统化。一节成功的单元整理复习课后，应该给学生留下的是知识体系或知识网络，而不能还是零散的、碎片化的知识点，所以单元整理和复习的核心环节就在于知识的梳理。教师应引导学生按一定的标准对所学知识进行分析、对比、归类，使分散的知识变成一个整体，形成较为完整的知识体系。然而，不同知识间可能存在着横向或纵向间的逻辑关系，教师应该善于引导学生进行深入分析，然后连点成线，由线成面，由面成体，形成知识网络，进而帮助学生完善知识结构。

就像许老师的板书，这棵树便是整个知识网络，最后整个知识结构都能成功建构于学生的脑海，这便是单元整理复习后应该留给学生最重要的一部分——知识梳理后的知识网络或知识体系。

所以，一节单元整理复习课后，至少应该给学生留下一个清晰的知识网络结构或者知识网络体系。

让我们每位老师都重视单元整理复习课，并科学地去引导学生进行单元整理复习，使学生在加深对知识的理解和掌握后，建构出结构清晰、系统完整的知识网络，形成相对稳定的知识结构，甚至养成自主进行单元整理复习的好习惯，才是单元整理复习课的终极目标。