风险厌恶和广告促销下基于收益共享的补货协调政策
代建生 于诗妍
(昆明理工大学管理与经济学院)
1 研究背景
广告是创造需求和拓展市场的关键工具,是提高企业竞争力,占有市场份额的重要手段。无论是国外的“黑色星期五”还是国内的“双十一”促销活动,都给企业带来了可观的收益。2019年双十一,天猫、京东、拼多多和唯品会的成交金额分别达到2 684亿、705亿、205亿和107亿元,较2018年均有大幅增长,其中手机数码、家用电器、个人护理及美妆、服装和鞋包等行业占据销售榜前五[1]。但过量的广告投放可能导致供需不匹配,尤其是经营报童类商品的企业。报纸、流行服饰、电子创新产品等具有易蚀、易腐及销售周期短的特性,经营风险大,科学管理此类商品的库存至关重要。苹果手机的更新换代很快,越来越呈现出报童商品属性[2]。报童商品经营企业通常基于市场预测进行订货决策,但需求预测与最终实现并不一致[3],在某些情形下差异还非常显著。风险厌恶是很多中小企业的共同特征[4],在风险厌恶下,零售商倾向于订购比风险中性者更低的数量,从而更加偏离系统最优[5,6]。
为了降低因需求的不确定导致的经营风险,上游企业可为零售商提供需求实现后的补货机会,前提条件是供应链的运营能够满足补货的时间要求,品牌服装、疫苗、国际贸易商品、非畅销书籍等行业,通常允许零售商在一个销售周期重复订购有限几次[7]。通过补货,不仅能更好地满足顾客需求,且可在一定程度上修正零售商的订购决策对系统最优的偏离,这在零售商风险厌恶下起到的作用比风险中性情形更佳。尽管如此,允许补货将导致零售商的订购行为更趋保守,这是因为在市场需求较差时,较少的商品采购可减小销售剩余损失;而在市场需求较好时,补货能够消除或减少订购量与实际需求的差异。由于顾客对商品的忠诚度不一样,且补货需要一定的提前期,因此,缺货将导致部分顾客的流失。顾客流失率依赖于补货提前期的长短、竞争者和替代商品的可替代性,以及顾客对商品品牌的忠诚度等。补货机会和顾客流失率对零售商的策略选择具有重要影响,零售商对待风险的态度将作用于上述影响过程。在供应链的运营使补货成为可能时,供应链是否应该实施补货政策?在零售商风险厌恶且广告促销下,是否存在政策机制能协调供应链?在什么情形下存在这样的政策机制?协调政策又有什么特征?本研究拟对上述问题进行回答,并特别关注收益共享的补货协调政策。当销售收入宜于被第三方所证实时,这一政策在商业实践中具有可行性。苹果公司在开展其iPhone业务时就使用了这一协调政策,Google AdSense也使用此政策来协调广告业务[8]。
2 文献综述
本研究与促销影响需求下的供应链协调文献,尤其是风险厌恶下的研究相关。在促销影响需求下,除了数量折扣政策之外,常见的协调政策均不能协调供应链[9,10]。为此,TAYLOR[11]设计了销售回扣和回购政策的组合机制。KRISHNAN等[12]考察了需求被观察到之后再采取促销努力的协调问题,并提出多个能实现渠道协调的机制安排。KUNTER等[13]及赵守婷等[14]指出,促销成本分担与收益共享机制的组合能实现对供应链的协调。HE等[15]设计了能协调供应链的销售折扣、惩罚与回购政策的组合机制。上述文献没有考虑风险偏好对协调政策的影响。已有研究表明:仅当供应链的节点企业不过于厌恶风险时,收益共享与回购政策才能协调供应链[8,16];特别地,即使能够实现渠道协调,也必须对适用于风险中性的协调政策参数进行修正[8,17]。在风险厌恶下,即使促销努力不可证实,收益共享或回购政策与数量折扣政策的组合也能完成渠道协调[18]。在零售商促销并拥有部分定价权下,代建生[19]分析了风险厌恶对协调政策的影响,并设计了收益共享、促销成本分担和最低限价政策的组合机制。本研究与这类文献的主要差异在于:上述文献均假定零售商没有补货机会,而本研究允许零售商在需求实现后补货。在一次订货下,收益共享政策仅涉及收益共享比例和采购价格两个参数;在允许补货下,收益共享政策包括3个参数:收益共享比例、采购价格和补货价格。本研究认为,在协调政策参数设计中,是否允许补货不改变采购价格与收益共享比例系数之间的关系,但补货价格的设定对补货政策能否协调供应链至关重要。
本研究与二次订购或紧急订购文献也是相关的。在这类文献中,部分研究探讨了风险厌恶对订货决策的影响问题。AGRAWAL等[20]、CHEN等[5]分别运用期望效用方法和CVaR方法研究了紧急订购的报童问题,但二者均未考虑紧急订货期间缺货顾客的流失。汪竣萍等[2]通过引入延迟供给率,在假定缺货发生时存在顾客流失下,通过数值实验表明,零售商的风险厌恶程度越大,其初次订购量越少。本研究通过数理分析确认了汪竣萍等[2]的研究结论。
还有部分文献探讨了二次订购下的协调问题[3,21]。LINH等[22]讨论了允许二次订购下如何使用收益共享政策来协调供应链,并指出,要实现渠道协调,政策参数须满足以下特征:初次订购和二次订购的批发价格均小于对应的生产成本,且收益共享比例是批发价格的线性增函数。尚文芳等[23]从信息更新的视角分析了柔性期权政策的协调问题,其中零售商拥有两次期权购买机会。上述文献探讨的是两个周期的订货协调问题,在两个经营周期里商品售价可以不同,且零售商在二次订货时仍面临需求不确定问题;而本研究在单个经营周期里探讨订货协调问题,其中紧急订货发生在需求实现之后。
与本研究类似,王圣东等[24]也在一个经营周期里考察二次订货的协调问题,并提出一个改进的收益共享政策来协调供应链。但与本研究存在以下差别:①王圣东等[24]在风险中性下进行研究,而本研究在风险厌恶下进行讨论;②王圣东等[24]仅仅关注商品订购的协调问题,本研究关注商品订购和广告促销两个决策变量的协调问题。张小娟等[25]探讨了零售商通过仓单融资进行二次订购的收益共享政策,其中二次订购发生在销售之前,两次订购的批发价格相同。在本研究中,零售商的补货行为发生在需求实现之后,两次订购的批发价格不同;特别地,本研究关注如何设定两次订购的批发价格来协调供应链,尤其是补货价格。最近,刘彩云等[26]在与本研究相同的背景下考察收益共享政策的协调问题,但他们没有讨论协调政策的可行域,以及外生变量对政策参数的影响。本研究拟刻画收益共享协调政策参数之间的关系,以分析风险厌恶、商品残值、延迟供给率及紧急生产成本对协调政策的联合影响。
3 问题描述与假设
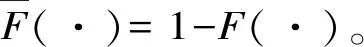
假设1广告促销可增大商品市场需求。
零售商借助促销广告等手段可扩大商品市场需求。在广告促销下,商品市场需求为a+ξ,其中a≥0。广告促销的成本为C(a),它关于a严格凸增、二阶可导,且满足C(0)=0及C′(0)=0。
特别地,由于广告具有延迟效应[27],促销广告需在商品销售前进行投放。
假设2供应商提供补货政策,允许零售商在需求实现后补货;延迟供给率为λ∈[0,1]。
在商品销售前,零售商根据对市场需求的预测确定商品订购数量q,采购价格为w1。如果市场需求小于商品订购数量(a+ξ≤q),则需求得到满足,剩余商品无残余价值;如果市场需求大于商品订购数量(a+ξ>q),则零售商可以实施二次采购进行补货,第二次采购的价格为w2。为了便于区分,后文将w1和w2分别提及为采购价格和补货价格,将第一次采购和第二次采购分别提及为正常采购和补货采购。讨论需求实现后允许补货(紧急订购)的文献包括CHEN等[5]、AGRAWAL等[20]、王圣东等[24]、刘彩云等[26]。
终端顾客拥有不同的品牌忠诚度,当市场需求大于正常采购量时,一部分需求暂时得不到满足的顾客会选择其他替代商品,而另一部分比较忠诚的顾客则会继续等待。延迟供给率指顾客愿意接受延迟供给的商品数量与缺货数量之比。
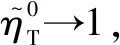
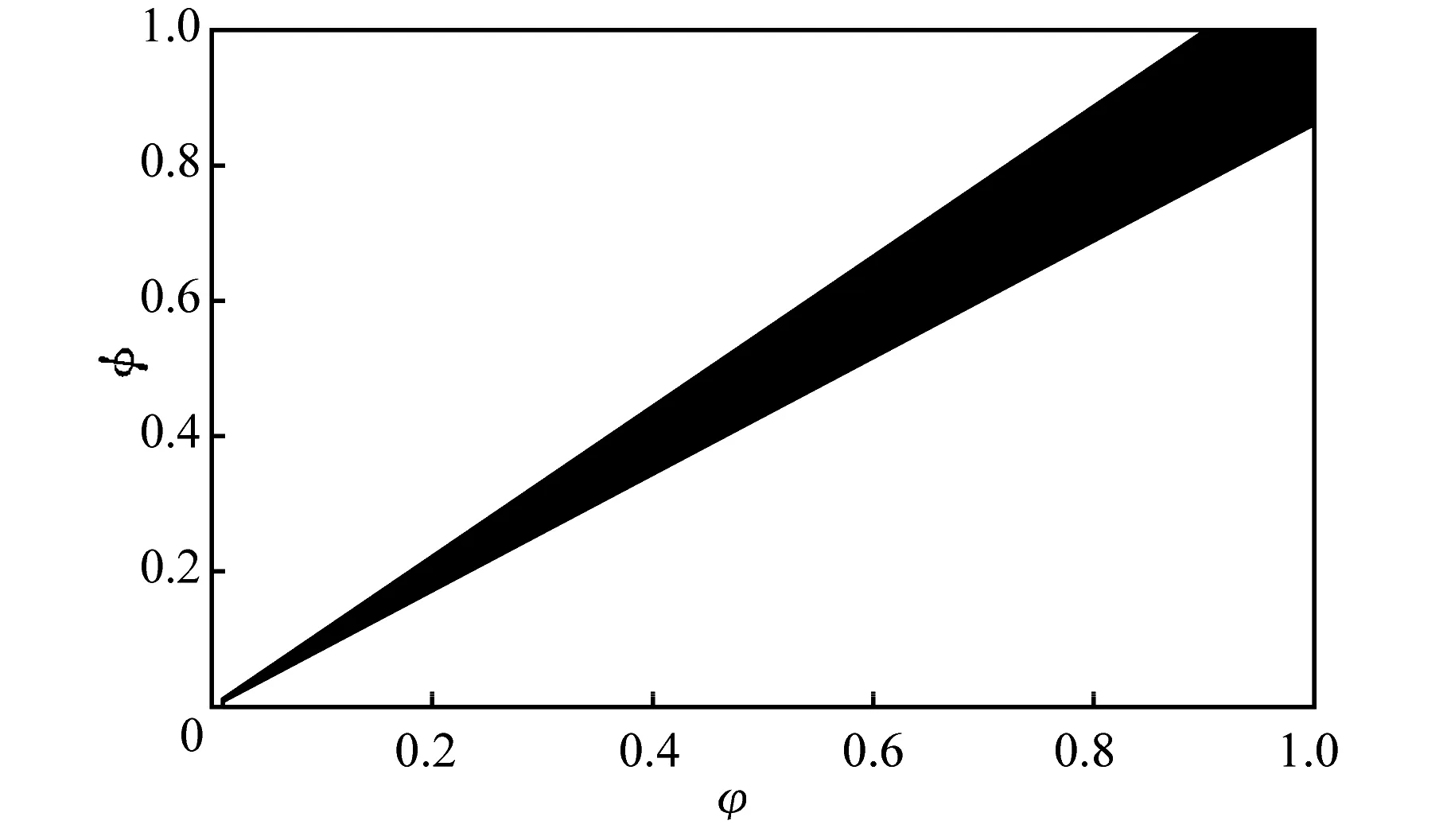
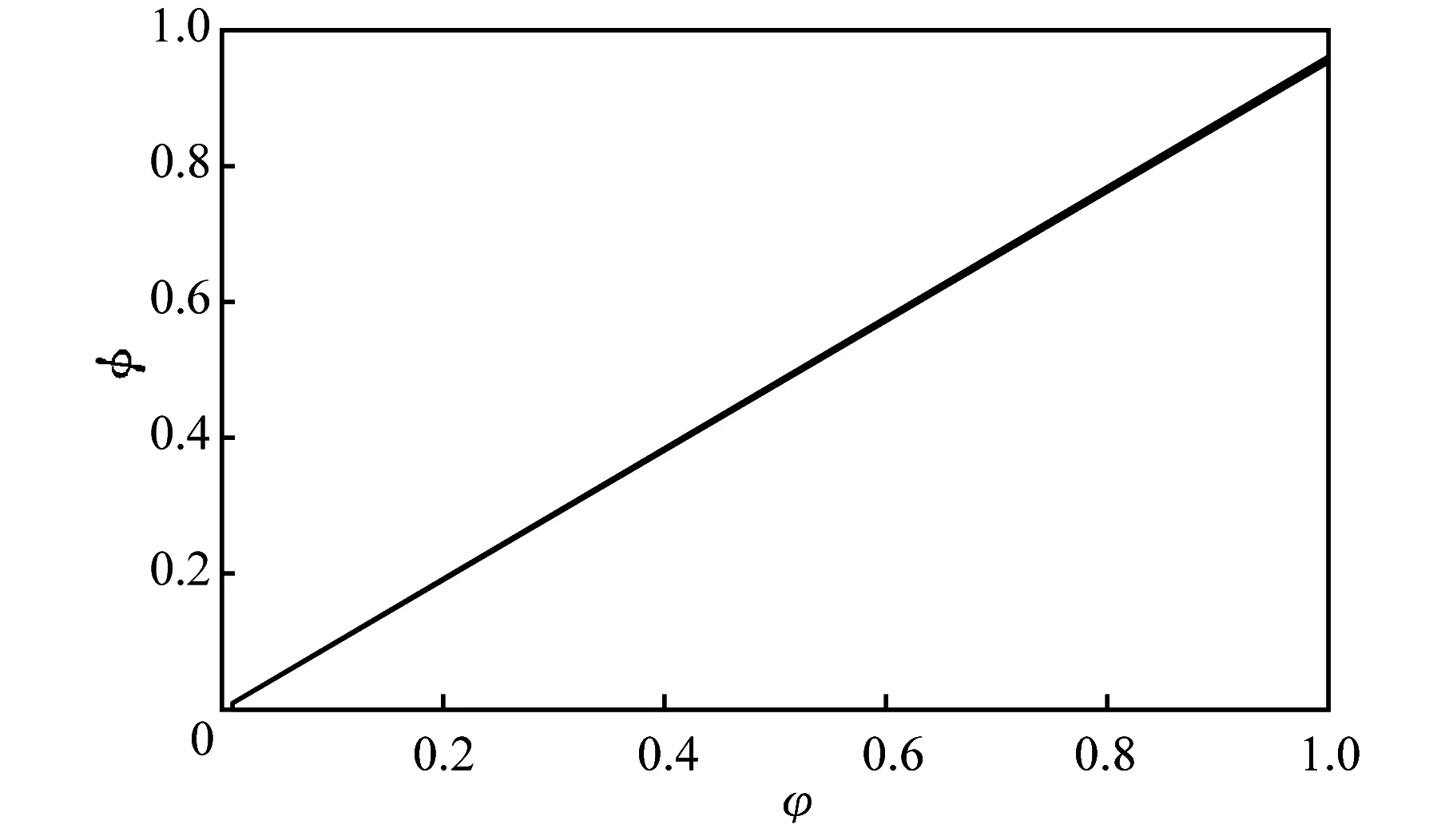
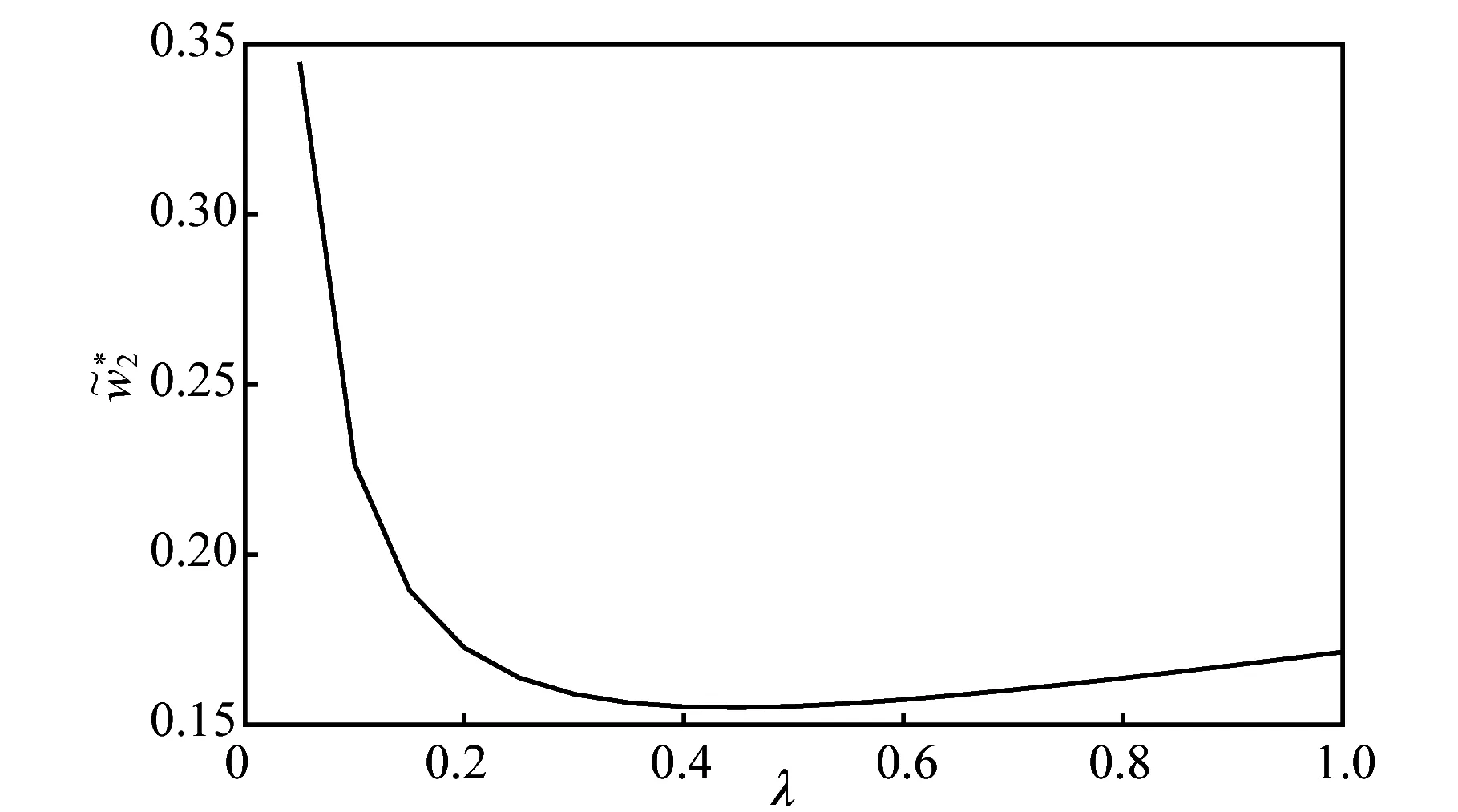
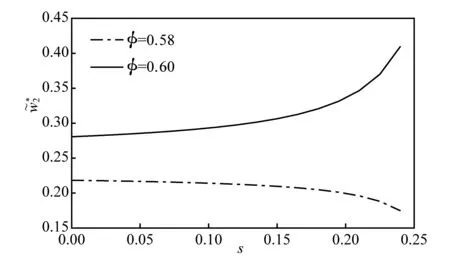
假设3供应商有两种生产模式,正常生产模式和紧急生产模式,生产成本分别为c1和c2,且有0 正常生产模式的生产提前期较长,而紧急生产模式的生产提前期较短。紧急生产模式下的生产成本c2大于正常生产模式的生产成本c1。后文将c1和c2分别提及为正常生产成本和紧急生产成本。 在后文构建的模型中,不排除c1=c2这种可能性。如果要满足零售商补货的时间要求,只能启动紧急生产模式进行生产,则c1 假设4供需双方采用收益共享和成本分担政策来协调供应链。 供需双方决定采用收益共享和广告成本分担的政策组合(w1,w2,φ,φ)来协调供应链。在这一政策组合下,采购价格和补货价格分别为w1和w2,销售收入实现后,零售商和供应商共同分享销售收入,分享比例分别为φ和1-φ;广告成本分担比例分别为φ和1-φ,这里约定φ∈(0,1)及φ∈(0,1)。 在政策(w1,w2,φ,φ)下,零售商确定订货和广告策略(q,a),其利润函数为 πR(q,a)=φp[min{q,a+ξ}+λ(a+ξ-q)+]- w1q-w2λ(a+ξ-q)+-φC(a); (1) 给定零售商的策略(q,a),供应商确定产量y,其利润函数为 πS(y;q,a)=(1-φ)p[min{q,a+ξ}+λ(a+ξ-q)+]+ w1q-c1y+w2λ(a+ξ-q)+-c2[λ(a+ξ-q)+- (y-q)]+-(1-φ)C(a)。 (2) 假设5协调政策参数满足以下关系:w1>0,w2>0,0<φp-w1 在商业实践中,采购价格和补货价格均为正;否则,零售商有激励采购无穷多的商品。 在收益共享政策下,要使供应商和零售商都从商品交易中获利,在正常采购时要求φp-w1>0且(1-φ)p+w1-c1>0,这与0<φp-w1 正常采购发生在市场需求实现之前,面临需求不确定性风险;而补货采购发生在需求实现之后,没有不确定性风险,但在补货期间有可能流失部分顾客。如果市场需求大于正常采购量,未满足的需求只有λ部分会转化为实际需求。如果φp-w1≤λ(φp-w2),零售商将把采购推迟到需求实现之后进行,因为补货采购给零售商带来的收益大于正常采购,即使存在部分顾客流失。 假设6博弈次序如下:供需双方通过谈判确定协调政策(w1,w2,φ,φ),在政策确定后,零售商率先行动,选择策略(q,a);供应商后行动,在观察到零售商的策略后确定产出策略y,且有y≥q。 如果供应商接受零售商的订单,则产生法律效力,零售商的订单必须得到满足,由于补货商品具有一定的生产提前期,因此,供应商的正常生产量不小于零售商的正常采购量。在供应商提供补货政策下,供应商预期到零售商会补货,有可能生产比正常订单数量更多的商品。 假设7风险厌恶零售商采用条件风险价值方法作为决策准则。 在技术上,本研究使用条件风险价值(CVaR)方法作为风险厌恶零售商的决策准则。CVaR方法具有良好的结构和计算特性,近年来在运营管理领域得到广泛应用[4,5,28,29]。 给定某一置信水平η,设零售商的利润函数为πR(·),则其CVaR为 (3) 式中,R表示实数域,E[·]是数学期望算子;η∈(0,1]是零售商的风险厌恶系数,η越小,零售商越厌恶风险,η=1对应着风险中性的情形[30]。 在集中决策下,整个供应链视为单一企业,不存在订货决策问题,在生产量为y并且广告投放水平为a下,供应链的利润πSC(y,a)=pmin{y,a+ξ}-c1y+(p-c2)λ(a+ξ-y)+-C(a)。供应链的问题是:确定y和a以最大化E[πSC(y,a)],即P1:maxy,aE[πSC(y,a)]。E[πSC(y,a)]是关于y和a的(联合的)严格凹函数,问题P1存在唯一最优解(yI*,aI*)。 命题1供应链的最优策略(yI*,aI*)由以下两式联合确定: F(yI*-aI*)=ηT; (4) C′(aI*)=p-c1, (5) 式中,yI*是λ的严格减函数,是c2的严格增函数。 延迟供给率提高,在允许补货下,缺货导致的机会损失减小,则应减小正常生产产量。紧急生产成本上升,使用此模式进行生产变得不经济,则应扩大正常生产产量。 下面在协调政策给定下讨论分散决策问题:首先讨论零售商的决策,再讨论供应商的决策。 采用与DAI等[6]相同的方法,可证v*(q,a)=λ(φp-w2)[a+F-1(η)]+[(φp-w1)-λ(φp-w2)]q-φC(a),使得g(v,q,a)取极大值。将v*(q,a)代入g(v,q,a),并令g(q,a)=g(v*(q,a),q,a)。 命题2给定(w1,w2,φ,φ),如果φp>w1且φp-w1>λ(φp-w2),零售商的最优策略(q*,a*)由以下两式联合确定: (6) φC′(a*)=φp-w1, (7) 式中,q*是η的严格增函数,是λ的严格减函数,是w2的严格增函数。 证明用gi(i∈{q,a})表示g(q,a)关于q和a的一阶偏导数;用gij({i,j}∈{q,a})表示g(q,a)关于q和a的二阶偏导数,则有gqq=-η-1[(φp-λ(φp-w2)]f(q-a),gqa=gaq=η-1[(φp-λ(φp-w2)]f(q-a),gaa=-η-1·[(φp-λ(φp-w2)]f(q-a)-C″(a)。由λ∈[0,1],φ∈(0,1)且w2>0,有φp-λ(φp-w2)=(1-λ)φp+λw2>0,利用这一事实可证,g(q,a)关于q和a的海赛矩阵是严格负定阵。令gq=0且ga=0,即 gq=[(φp-w1)-λ(φp-w2)]- η-1[(φ(p-s)-λ(φp-w2)]F(q-a)=0; (8) ga=λ(φp-w2)-φC′(a)+ η-1[φ(p-s)-λ(φp-w2)]F(q-a)=0。 (9) 联立求解上述两个方程可得式(6)和式(7)。利用式(6)和式(7),易证∂q*/∂η>0,∂q*/∂λ<0及∂q*/∂w2>0。 q*关于λ递减和关于w2递增,其隐藏在背后的逻辑与“yI*关于λ递减和关于c2递增”是一样的。在风险厌恶下,零售商行为更加保守,零售商越厌恶风险,其订货量就越小,DAI等[6]在一次订购机会下得到相同的结论,命题2则将DAI等[6]的结果拓展到允许补货的情形。 下面简单讨论命题2的两个假设条件:①φp-w1>λ(φp-w2);②φp>w1。这两个条件均已总结在假设5中。若条件①不成立,则由式(8),并注意到φp-λ(φp-w2)=(1-λ)φp+λw2>0,有gq<0,故有0≤a*≤q*=0;若条件①成立但条件②不成立,则由式(9),有ga<0,故有0=a* 如果λ=1,条件φp-w1>λ(φp-w2)意味着w1 令πS(y)=πS(y;q*,a*),则有πS(y)=(1-φ)p[min{q*,a*+ξ}+λ(a*+ξ-q*)+]+w1q*+w2λ(a*+ξ-q*)+-c1y-c2[λ(a*+ξ-q*)+-(y-q*)]+-(1-φ)C(a*)。 (10) 利用引理3可对引理2进行精炼,即引理2的结论对任意φ∈(0,1)成立。 (11) ②当λ=0时,有 (12) 证明只证明情形①,情形②类似,略去。 由w1>0且φp-w1>λ(φp-w2),有0<(φp-w1)-λ(φp-w2)<φp-λ(φp-w2)。要使式(13)成立,必然有η>ηT。由式(13)和式(14)组成的方程组只有两个方程,但需要设定的政策参数有4个,一般地,上述方程组的解拥有两个自由度。选取φ和φ作为自由变量,联立求解式(13)和式(14),可得 (15) (16) φ∈(max{A(φ),B(φ)},min{1,H(φ)})。 (17) φ∈(0,1)。 (18) 式(15)~式(18)联合给出式(11)。 刘彩云等[26]在与本研究相同的背景下探讨了收益共享政策的协调问题,得到与定理1相同的临界条件;但他们对政策参数之间关系的刻画过于粗略,尤其是没有刻画自由参数变量的取值空间,导致其所定义的部分协调政策在现实中不可行。代建生等[8]在一次订货下刻画了协调性收益共享政策参数的关系,与定理1中λ=0的情形一致,即式(12)。如果没有补货机会,补货价格无关紧要,由式(11)刻画的政策参数φ的取值空间收缩为一点(由引理2,当λ=0时,A(φ)=B(φ)=H(φ)=ηφ)。KUNTER[13]在风险中性下对收益共享政策参数之间关系的刻画,与λ=0且η=1的情形一致。 根据定理2,在协调政策设计中,要平衡好零售商的收益和成本,且统筹协调零售商的两类成本:商品采购成本和广告成本。特别地,当零售商的收益共享比例上升时,应同时增大采购价格和补货价格,使得零售商分享的收益和承担的成本相匹配;当零售商分担的促销广告成本比例上升时,则应同时减小采购价格和补货价格——若广告成本上升,则商品采购成本下降。 推论1相对于一次订货情形,允许补货使得供应链的协调更有可能实现。 这个结论似乎有违直觉。由命题2,有∂q*/∂λ<0,既然λ=0对应着一次订货情形,允许补货将诱导零售商选择更小的采购量(似乎更加偏离系统最优,导致协调难以实现)。但在允许补货下,系统最优产量yI*也小于一次订货情形,且λ对yI*的影响大于对q*的影响,即在允许补货下,相对于零售商最优采购量的减小,系统最优生产量下降得更多,从而使得更加厌恶风险的供应链也有可能实现协调。 令λη=((1-η)p-c1)/((1-η)(p-c2))。 推论1和定理3揭示了以下管理洞见:①如果通过补货能够满足部分缺货顾客的需求,那么供应商应提供补货政策,而零售商应实施补货策略;②提高顾客忠诚度,缩短生产提前期,尤其是紧急生产模式的提前期,有助于减小顾客流失率,提高延迟供给率,从而实现供应链的协调。这是因为延迟供给率与顾客忠诚度和补货时间有关,为尽快满足缺货顾客的需求,供应商应加快商品生产进度,并以更快的物流速度向零售商补货。 如果供应商只有一种生产模式,或用正常生产模式即可满足补货的时间要求,则c2=c1,在这种情形下,无论零售商的风险厌恶程度如何,只要延迟供给率足够高,供应链的协调就有可能实现。特别地,如果在补货期间没有顾客流失,供应链的协调总可以实现。 (19) (20) 定理4揭示了以下管理启示:①当供应商引进了新的生产模式使得补货成为可能,从而需要设定补货协调政策时,不必修正原来执行的采购价格;②零售商的风险厌恶程度、延迟供给率及紧急生产成本变化时,只需调整补货价格,采购价格保持不变。特别地,零售商越厌恶风险,或者紧急生产成本越高,补货价格应设定得更高。 (21) 命题3Λ关于λ严格递增。 由命题3,补货价格的设定应确保Λ关于λ严格递增,其中,Λ表示零售商在商品补货中实现的单位净收益与延迟供给率的乘积。 当商品需求对广告促销不敏感或广告促销不是零售商的策略选项时,零售商不会投放广告,在这种情形下,广告成本分担机制没有意义。下面考虑政策机制(w1,w2,φ)。前文的讨论也适用于零售商不促销的情形,技术上,若零售商不促销,可将a视为恒等于0。在集中决策下,有yI*=F-1(ηT)。在分散决策下,给定协调政策(w1,w2,φ),零售商和供应商的策略分别为q*=F-1(η((φp-w1)-λ(φp-w2))/(φp-λ(φp-w2)))和 要实现渠道协调,政策(w1,w2,φ)须满足假设5及式(22)。 (22) 政策(w1,w2,φ)有3个参数,相互之间的关系仅由式(22)确定,因此,式(22)的解有两个自由度。 (23) 前文假定剩余商品的残余价值为零。一般地,对于季节性商品或短生命周期商品而言,不考虑残余价值是合理的,如月饼、牛奶等易腐食品。不过在现实中,也存在残余价值不为零的情形,如流行服饰[31,32]。那么,商品残值对前文研究结论是否有影响呢?下面讨论这一问题。 假设3′商品残值为s,且与生产成本满足以下关系:0≤s 假设4′供需双方采用收益共享和成本分担政策来协调供应链。 如果零售商采购的商品出现剩余,其残值由零售商和供应商共同分享,双方的分享比例与销售收入的分享比例相同。若供应商过量生产,超过采购量的商品残值则由供应商获得。两者的利润函数分别为 (24) s[(y-q)-λ(a+ξ-q)+]+。 (25) 假设5′政策参数满足:w1≥φs,w2≥(1-φ)s,0<φp-w1 残余价值越大,超额生产的损失越小,因此,在集中决策下,供应链应该扩大正常生产的产量,在分散决策下,零售商将采购更多的商品(这促使供应商增大正常生产产量)。 下面实施数值分析,参数设定如下:p=1,c1=0.4,c2=0.6,s=0.2,λ=0.6,η=0.95,w1=0.2,w2=0.3,φ=0.4,φ=0.6,市场需求服从参数为0.001的负指数分布,广告成本函数C(a)=0.001a2。给定上述参数的取值,供应链的最优策略(yI*,aI*)=(1 330,300),零售商的最优策略(q*,a*)=(1 193,250)。 渠道协调下φ的取值空间关于φ的变化关系见图1,其中当φ=0.5时,φ的取值空间为(0.431,0.554)。一般地,φ的上下界关于φ均是(分段)线性的。φ的取值空间还依赖于s和λ等其他参数,当s=0.35,λ=0.2且其他参数取值不变时,φ的取值空间关于φ的变化关系见图2。由图1和图2可知,在由式(11)刻画的协调政策下,其政策参数拥有两个自由度,其中φ可以任意设定,而φ虽可自由设定,但其选择并非是完全自由的,在某些情形下,其选择空间将极其有限。 图2 协调政策的可行域(s=0.35,λ=0.2) 表1 协调政策参数之间的关系 图关于λ的变化曲线 图关于s的变化曲线 零售商的风险偏好、广告促销以及上游企业是否提供补货机会等因素,都会对零售商的订购决策产生重要影响。本研究在零售商风险厌恶且实施广告促销下,探讨收益共享的补货协调政策,刻画了协调政策的可行域及参数之间的关系,分析了紧急生产成本、延迟供给率、残值以及风险厌恶对政策参数的影响。 本研究得到以下结论:①无论是否允许补货,只要零售商的风险厌恶程度低于某一临界值,借助广告成本分摊机制,收益共享政策就可协调供应链。②补货政策增大了风险厌恶供应链被协调的可能性,延迟供给率越高,残值越小或紧急生产成本越低,渠道协调越有可能实现。特别地,在单一生产模式下,无论风险厌恶程度如何,只要延迟供给率足够高,渠道协调就可实现。③在政策参数设计中,是否允许补货不改变采购价格与收益共享及广告成本分担比例两个系数之间的关系,但补货价格的设定对渠道协调至关重要。补货协调政策拥有两个自由度,其中只有一个参数拥有完全的自由度,另一个自由参数的取值空间依赖于完全自由参数的选取。协调政策参数具有以下关系:采购价格和补货价格是零售商收益共享(广告成本分担)比例的线性增(减)函数;零售商的风险厌恶、延迟供给率、残值或紧急生产成本的变动只影响补货价格,与采购价格无关。 本研究揭示了以下管理启示:①如果供应链的运营能满足补货的时间要求,供应商应提供补货政策;若因新的生产模式使补货成为可能,在设定补货协调政策时,只需关注补货价格的制定,不必修正采购价格。②要尽可能缩短紧急生产的提前期,提高顾客忠诚度,以减少缺货顾客流失率。③在政策参数设计中,应平衡好零售商的收益与成本,并统筹协调采购和广告成本两者之间的关系。特别地,若要提高零售商的收益分享比例,则应同时(线性地)提高采购价格和补货价格;若要提高其广告成本比例,则应同时(线性地)减少采购价格和补货价格。④零售商越厌恶风险,或紧急生产成本越高,则应设定更高的补货价格,但采购价格保持不变。4 集中决策
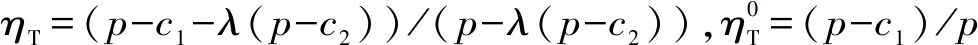
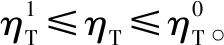
5 分散决策
5.1 零售商的订货和广告决策
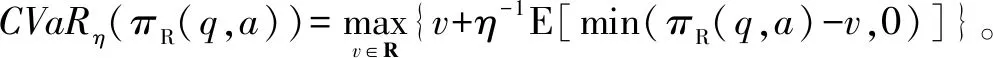
5.2 供应商的生产决策
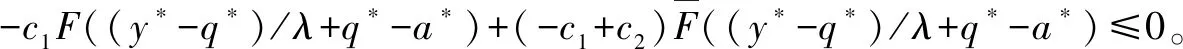

6 收益共享的补货协调政策
6.1 协调政策参数设计

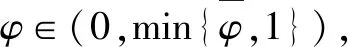
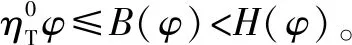
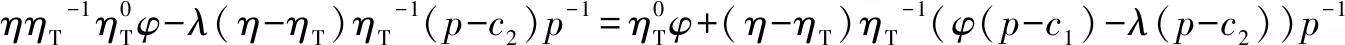
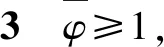

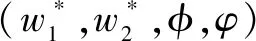

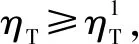
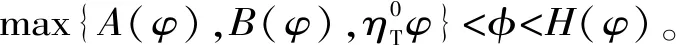
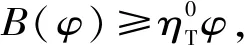
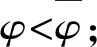
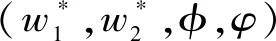
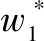
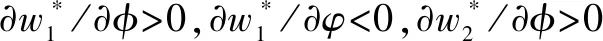
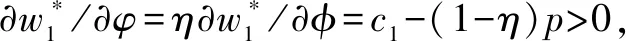
6.2 补货政策对渠道协调的影响分析
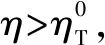
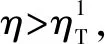
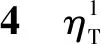
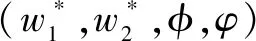
6.3 外生参数对补货协调政策的影响分析
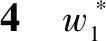
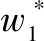
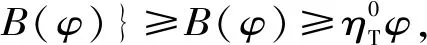
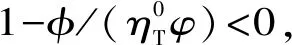

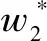
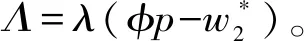
6.4 特例:无广告促销情形
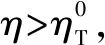
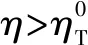
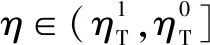
6.5 进一步讨论
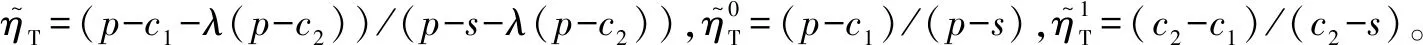
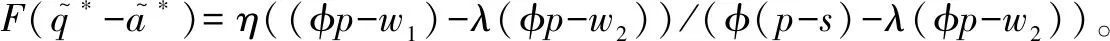
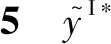
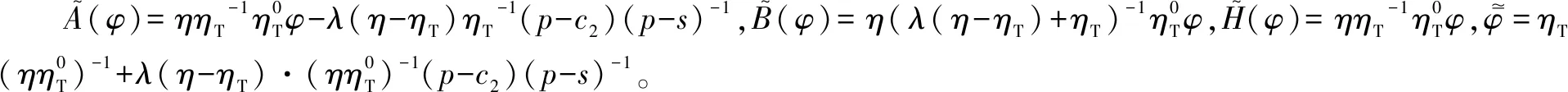
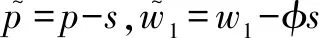
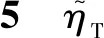
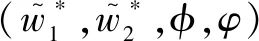
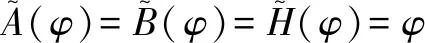
7 数值分析

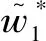

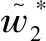
8 结语

