煤层割理结构及其对井壁稳定的影响研究
王跃鹏,孙正财,刘向君,梁利喜
(西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500)
煤层气是一种自生自储的非常规天然气,资源潜力巨大,已引起了业内的广泛关注[1]。在钻井过程中,煤层井壁失稳不仅会影响钻井安全,导致起下钻困难、卡钻事故、降低钻井效率等,而且会给取心作业的安全和质量带来威胁,给后期储层改造带来一定的困难。由于煤岩自身割理发育使得煤岩基质连续性差和非均质性程度高,传统连续介质力学井壁稳定模型已不再适用于煤层这种破碎性地层[2-3],必须进行相应有针对性的研究。
煤岩井壁失稳现有的主要力学研究方法包括基于连续性介质力学方法和基于非连续性介质方法。申瑞臣等[4]认为解决非连续性问题最常用的方法为采用拟合方法(如Hoek-Brown公式)、断裂力学或离散元方法。刘向君等[5]基于连续介质力学理论,分析了岩石软弱面产状、摩擦系数2个方面对井壁稳定性的影响。GENTZIS[6]基于FLAC软件分析了煤层水平井在欠平衡钻井和过平衡钻井条件下的井壁稳定性。屈平等[7](2009)用应力强度因子描述了裂纹的受力集中程度,提出了可以定量判断节理煤层直井或水平井井壁是否稳定的节理煤层井壁稳定评价模型。非连续介质方法解析法研究煤层中具有代表性的为陈勉[2]等基于非连续性介质力学方法建立的可以预测煤层坍塌压力的离散构元模型。离散元数值模拟方法被认为更加适合模拟煤岩行为,可解决力学分析方法无法定量描述割理产状对煤层井壁稳定的影响的问题[8]。李嗣贵、孙正财、尹虎等[9-11]依次利用离散元方法分析了煤层井周应力状态、裂缝张开情况、裂缝方向,井眼尺寸、井眼密度以及煤层气井注入气体增压过程流体在面割理和端割理方向的运移引起的煤层井壁失稳问题。屈平等[12](2011)基于三维离散元软件(3DEC)分析井底压力、割理密度等因素对煤层水平井井壁稳定的影响。
上述学者基于不同的研究方法研究了煤层井壁稳定,认为在各向异性应力储层中,煤层更容易产生破裂和坍塌,当面割理与井眼走向平行时,井壁最不稳定。但考虑地应力和割理角度对煤层井壁稳定影响的系统研究较少,现有的研究已知煤层地应力对井壁稳定的影响较大,割理角度的影响亦不容忽视。鉴于此,从力学角度出发,分别采用最大位移和归一化塑性区域半径2种评价方法,结合研究区煤岩基础物性、宏微观结构、力学强度参数和地应力状态并借助通用离散元方法,研究了煤岩力学井壁稳定性影响因素,分析了煤岩力学井壁失稳机理。研究成果不仅为钻井过程中预测煤层井壁稳定提供重要的参考依据,而且对安全钻井和高效开发煤层气资源具有重要意义。
1 煤岩割理结构
煤岩是具有双重孔隙介质的岩石,煤岩割理类型和分布特征对其力学性质和基础物性影响较大,同时割理分布特征也是导致煤岩力学特性各向异性的内在原因之一。
1.1 煤岩的宏观结构
使用HKGP-3型致密岩心气体渗透率孔隙度测定仪测得研究区煤岩的孔隙度范围值为0.02%~18.10%,平均孔隙度为6.85%,渗透率范围区间为(0.000 3~0.06)×10-3μm2,平均渗透率为0.02×10-3μm2。煤岩岩样具有大于0.1 mm可用肉眼观察的宏观裂隙,通过宏观观察和标记的方法对研究区煤岩割理密度进行测定。
煤体结构以原生结构为主,表面层状结构明显,可见镜煤条带。部分岩样裂隙发育,面割理和端割理裂隙特征较明显,近似相互垂直发育,同时又垂直于煤层层面,其中面割理延伸较长,端割理随机分布在面割理之间。可以观察到在出现镜煤条带的位置割理密度较大,面割理大致平行连续分布整个煤块,面割理之间距离较小,通过宏观观察和统计得出面割理密度为(19~28)条/10 cm,端割理密度为(17~27)条/10 cm。
1.2 煤岩的微观结构
利用型号为Quanta450的扫描电镜对煤岩微观结构作进一步分析,可以直观地发现煤岩具有较高的割理、裂隙发育程度(图1),观察到较多的面割理和端割理,面割理和端割理近似垂直发育,连通性较好,面割理延伸长度比端割理长,且清晰观察到面割理的宽度也比端割理大。随着放大倍数增加,割理特征更加明显,在高放大倍数下观察到面割理宽度约为1~10 μm,端割理宽度约为0.4~5 μm。
2 离散单元法基本原理

图1 煤岩割理形态扫描电镜Fig.1 SEM of cleat morphology
离散元法是专门分析非连续性介质问题的有效数值模拟方法[13],将所研究的岩体看成是由断层、节理、裂隙等弱结构面切割成的刚性或者可变性块体,块体与块体之间通过边界接触力相互联系,允许岩块平移、转动和变形,而节理面可被压缩、分离或滑动。
采用在刚性块体之间设置不同种类弹簧和阻尼的方法来反映材料的应力—位移关系,直至平衡。由牛顿第二定律得到各个块体的加速度,然后对时间进行积分,算出所研究块体的速度、位移,最终得出块体的变形量,块体在位移矢量方向发生调整时,又会更新接触面上的力和力矩,直到所有块体达到平衡状态或某种状态。
每一时间步的速度方程:
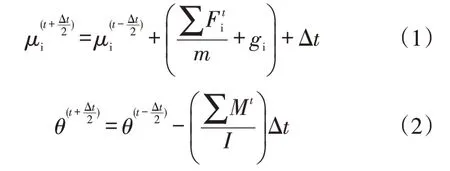
式(1)—式(2)中:μi为速度分量,m/s;t为时间,s;Δt为时间增量,s;∑Fi为作用力,N;m为块体在形心处质量,kg;gi为重力分量,m/s2;θ为块体的角速度,rad/s;∑M是总力矩,N·m;I为惯性矩,m4。
总控制方程:
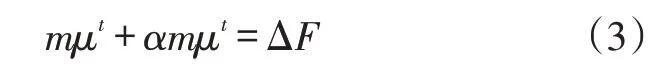
式中:m为块体在形心处质量,kg;μ是为位移增量,m;α为阻尼系数;ΔF为力增量,N[14]。
离散元表示岩体的节理为形成于两个块体边缘的接触面。该接触决定了接触的类型和最大的间隙。两个相互连接的块体间的相互作用可以由法线上的刚度,切线上的刚度和内摩擦角表示[13].。由弹簧的变形判定在接触面发育的力的大小,可转换为法向力Fn和剪切力ΔFs。
物理方程包括:

式(4)—式(5)中:Fn为法向力,N;Kn为法向刚度系数,MPa·m;δn为单元之间叠合尺度,m;ΔFs为剪切力增量,N;Ks为剪切刚度系数,MPa·m;δs为单元之间相对位移,m。
式(4)和式(5)只能表示在弹性条件下,在塑性条件时需要考虑岩体破坏条件,即在塑性剪切破坏的情况需要在每次计算(迭代)时都要检查剪切力。由Mohr-Coulomb准则可以得出每个块体接触点最大切向应力:
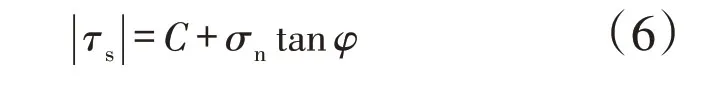
式中:|τs|为切向应力,MPa;C为块体内聚力,MPa;σn为法向应力,MPa;φ为内摩擦角,°。
3 数值模型的建立
为了尽可能模拟地层的实际情况,将模型中割理的迹长、隙宽作为随机变量以满足割理在地层中的随机分布。根据研究区煤岩的割理结构特征建立煤层井眼模型[15](图2),模型尺寸为2 m×2 m,井眼直径为215.9 mm,面割理的角度为α1,两条面割理间的距离为d1,端割理的角度为α2,两条端割理间的距离为d2。计算时将煤岩基质作为块体,用可变形块体来模拟,本构方程选用摩尔—库伦模型,由于割理面为不连续面,本构方程选用摩尔—库伦节理模型[16]。
模型中煤岩力学参数通过研究区煤岩力学实验获得[17-18],具体参数如表1所示。
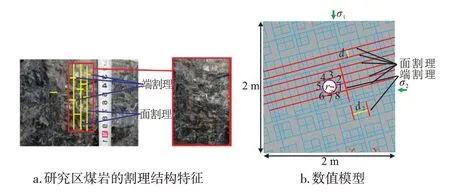
图2 煤层井眼模型Fig.2 Wellbore model of vertical wells in coal seams
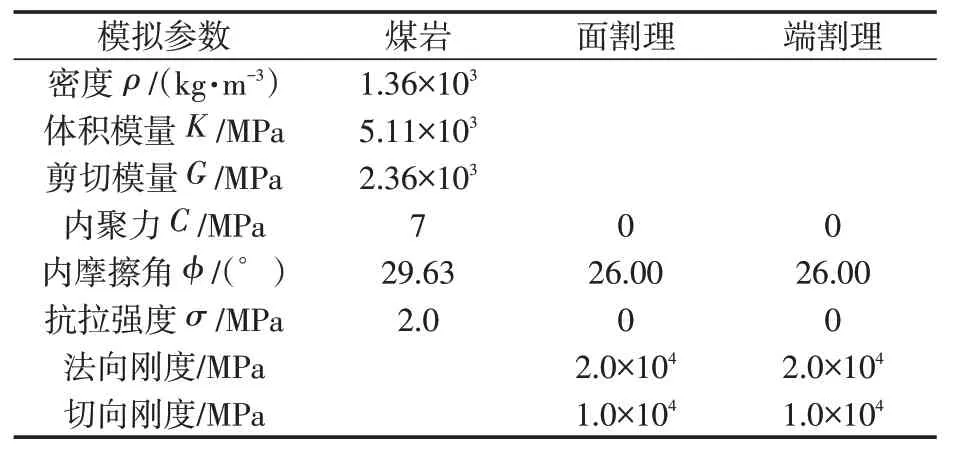
表1 煤岩力学强度参数Table1 Mechanical strength parameters of coal and rock
据研究区煤层气藏(深度约为800 m)的统计数据显示,垂向地应力σV约为20 MPa(压力梯度为2.55 MPa/100 m),水平主应力和深度之间存在很好的统计关系,水平最大主应力σH为(1.59~2.42)MPa/100 m,水平最小主应力σh为(1.55~2.25)MPa/100 m,无论是钻直井还是水平井,井段截面的井壁稳定问题均可以等效为二维平面应变问题,根据该地区测得的应力可知,σH/σh,σV/σH或σV/σh的范围均在1.0~2.0间,在数值模拟计算时仅考虑地应力比值大小。为研究地应力非均质性和割理角度对煤层井壁稳定的影响,分别考虑σ1/σ2比值为1、1.5、2三种情况;割理角度α1、α2分别为15°和285°、30°和300°、45°和315°、60°和330°、75°和345°、90°和360°六种情况;割理均匀分布,d1、d2分别为0.06 m、0.08 m,井筒压力设为0 MPa,模拟煤岩欠平衡钻井。
4 煤层井壁稳定性分析
在钻煤层气井时,井周应力超过煤岩割理抗拉强度或抗剪切强度时井壁将发生失稳现象,这是由于对于割理发育的煤层,地应力等因素会造成割理面的重新张开,会随着割理面发生应力释放,造成割理面发生剪切滑移使煤岩井壁剥落,因此可以根据井周剪切位移大小判断井壁是否稳定[19]。在数值模拟计算中,选择井周8个点(图2b)来记录监测煤层气井模型中块体的位移变化情况。在模型结束时,每个观察点都用来绘制钻孔剖面上的位移,使用最大位移和归一化的塑形区域半径2种方式来研究煤层气井的井壁稳定性。
4.1 最大位移
KARATELA 等[14]在研究地应力比值和裂缝方向对井壁稳定性影响时提出了一种评价井壁稳定性的方法,认为最大位移井眼尺寸总变化10%以内井壁是稳定的。根据此次模拟结果得到不同地应力比值条件下不同割理角度的井周煤岩位移(图3)。对应的最大井周位移随割理角度变化及井周位移随井周角的变化见图4。
将记录的井周8个点的位移根据式(7)估算出井眼尺寸总的变化。计算得知井周总位移变化为0.024 5 m,结合KARATELA 提出的评价井壁稳定性的方法得知最大位移在0.002 45 m 以内煤层井壁是稳定的,因此在评价煤层井壁稳定性时将最大位移为0.002 45 m作为判断井壁是否稳定的一个最佳值,即认为井壁最大位移大于0.002 45 m时,井壁失稳。

图4a为在不同地应力比值时最大位移随着割理角度α1的变化,图4b和图4d分别为σ1/σ2比值为1、1.5、2情况下的井周位移大小变化。李光泉[20]在井壁稳定性影响研究中指出,井眼对地应力σ1/σ2的大小很敏感。结合图3和图4a可知,随着地应力差异性增大,不同割理角度下井周最大位移变化幅度变大,煤层的井壁越容易失稳,但不同割理角度的增加幅度不同。当割理角度α1在30°~60°时,井周位移增大最为明显。
由图4b知,煤层在各向同性地应力(σ1/σ2=1)条件下,井周位移随割理角度的变化不大,井周最大位移为0.000 9 m,小于0.002 45 m,井壁处于最稳定的状态。说明在各向同性地应力条件下,割理角度对煤岩井壁稳定影响不大。
由图4c、图4d可知,随着地应力非均质性增大,井周位移随割理角度的变化越明显,差异性增大,割理角度对井壁稳定性的影响逐渐明显,井周煤岩位移最大的地方不一定平行于最大主应力方向。当σ1/σ2=1.5时,随着割理角度α1从15°增大至45°,井周煤岩位移明显增大,随着割理角度α1从45°增大至90°,井周煤岩位移又开始缓慢减小,在割理角度α1为90°时,井周位移变化很小。当σ1/σ2=2时,井周煤岩位移随着割理角度的变化规律和上述相同,只是地应力差异越大时,井周煤岩位移随着割理角度的变化也越明显。在地应力σ1/σ2=2,割理角度α1为45°时,最大位移0.003 6 m为最大,井壁相对最不稳定;当割理角度α1进一步增大时,井周最大位移有减小的趋势,秦启荣等[21]在裂缝对井壁稳定的影响研究中得出相似结论,裂缝倾角越大,裂缝对井壁稳定性的影响程度减小;当割理角度α1为90°时,即面割理垂直于最小主应力,平行最大主应力时,井周最大位移最小。这是因为此时相互垂直的割理面在地应力作用下相互滑动的可能性较小,限制了井周煤岩块体的移动,从而井壁相对保持稳定。
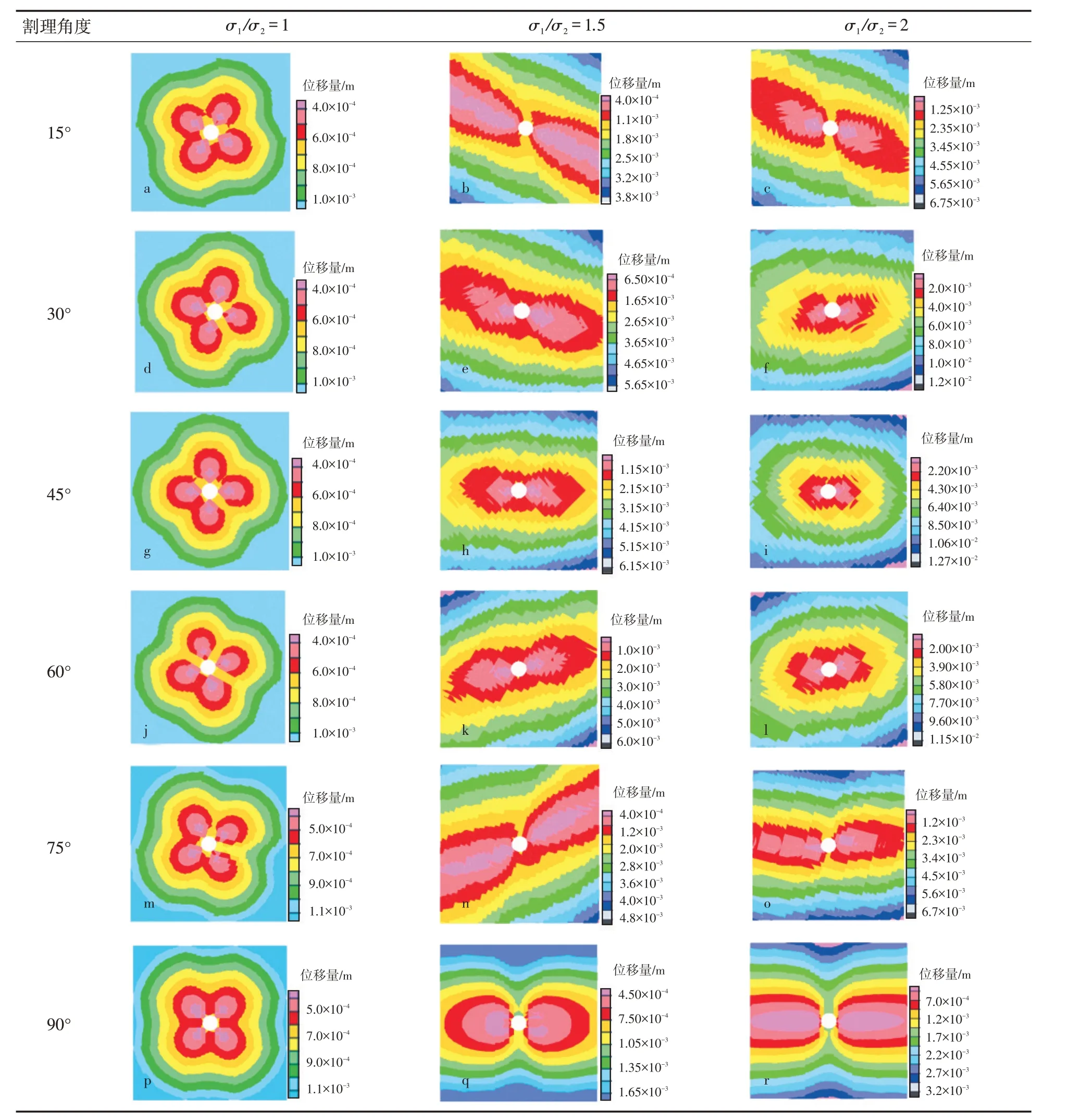
图3 不同割理角度下井周煤岩位移Fig.3 Displacement nephograms of coal and rock around under different cleat angle
此外,在各向同性地应力条件下,割理角度α1为30°时,井周最大位移最大,在各向异性地应力条件下,割理角度α1为30°或45°时,井周最大位移最大。这充分说明割理角度α1为30°或45°时,割理面在地应力作用下相互滑动的趋势较大。
4.2 归一化塑性区域半径(R/rw)
SALEHI[22]等通过井眼弹塑性模型结合FLAC3D软件分析了在欠平衡钻井时井眼力学稳定性,其在分析过程中利用归一化塑性区域半径来评价井壁稳定。如图5所示,当钻井时井周应力重新分布后在井周会产生平均半径为R的屈服区域。归一化塑性区域半径定义为井周平均屈服区域半径R与井眼半径比值(R/rw)。此外KARATELA 等[14]和HAWKES[23]分别在评价煤层水平井井壁和非连续裂缝性地层井壁稳定性时也采用了塑性区域半径评价方法。
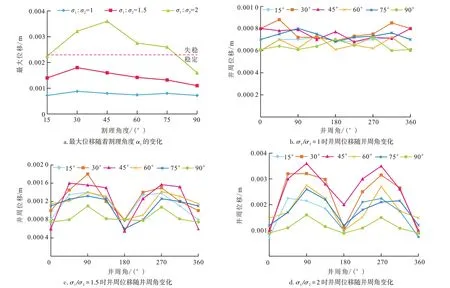
图4 井周位移变化分析Fig.4 Analysis of well circumference displacement
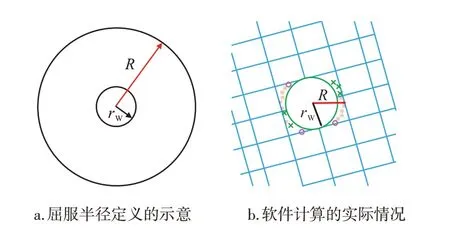
图5 平均屈服区域半径Fig.5 Average yield area radius
文中在评价煤岩井壁稳定时认为井眼周围归一化塑性区域半径(R/rw)小于1.25时煤岩井壁稳定。图5b中红色小圆圈表示已经破坏的块体单元,绿色叉号表示已经进入塑性屈服区域的块体单元,红色叉号表示已经达到塑性屈服极限的块体单元。
图6为地应力σ1/σ2比值为1、1.5、2时,分析对应的模拟结果所得到的井眼周围归一化塑性区域半径随割理角度的变化。
由图6可知,随着地应力比值σ1/σ2增加,煤岩井周归一化塑性区域半径增大,当σ1/σ2=2时,煤岩井周归一化塑性区域半径远大于σ1/σ2为1.5和1的状况,井壁相对最不稳定。这种变化趋势和井周最大位移随着地应力比值变化一致。井周归一化塑性区域半径在各向同性地应力及较低的地应力非均质性条件下(σ1/σ2在1.5 下),随着割理角度的变化分为2种状态:割理角度小于30°时,归一化塑形区域半径基本重合;割理角度大于30°时,σ1/σ2=1.5的归一化塑形区域半径大于σ1/σ2=1时。说明割理角度对井周塑性区域半径影响,受到地应力非均质性的影响,应力非均质性越大,井周塑性区域半径由割理角度影响产生的各向异性越明显。
割理角度15°、30°、45°、60°、75°、90°时在不同地应力非均质性下所对应的煤岩井周塑性屈服区域见图7。
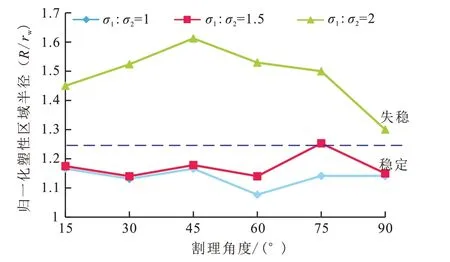
图6 不同割理角度下归一化塑性区域半径Fig.6 Normalized yield area radius at different cleat angel
由图7可知,割理角度一定时,随着地应力非均质性的增加,煤岩井周塑性区域范围增大,井壁相对越不稳定,且井周出现塑性区域的位置主要集中在割理面处。当σ1/σ2=1时,割理角度对井周塑性屈服区域半径影响不大。当σ1/σ2=2时,井周塑性屈服区域半径变化较大,割理角度对井周塑性屈服区域半径影响主要受地应力非均质性的影响。随着割理角度α1从15°增大至45°时,井周煤岩归一化塑性区域半径增大,随着割理角度α1从45°增大至90°时,井周煤岩归一化塑性区域半径开始缓慢减小,在3种地应力条件下,割理角度α1在90°时,井周煤岩归一化塑性区域半径最小,井壁保持相对稳定。

图7 不同割理角度下井壁塑性屈服区域Fig.7 Yield area at borehole wall with different cleat angles
5 结论
1)研究区的煤岩表面层状结构明显。在镜煤条带出现的地方,割理密度增加。面割理和端割理裂隙特征较明显,近似垂直发育,连通性较好。
2)在各向同性地应力下,井周最大位移和井周塑性变化区域半径变化都较小。随着地应力非均质性增大,不同割理角度下井周最大位移变化幅度增大,井周塑性区域半径由割理角度影响产生的各向异性更明显,煤层井壁更易失稳,但不同割理角度的增加幅度存在差异。因此割理角度α1对井周最大位移和井周塑性区域半径的影响,受到地应力非均质性的影响。
3)若研究区内某煤层气井测得水平最大主应力和水平最小主应力差值较小,则割理角度对直井井壁稳定的影响较小,可按连续性介质进行研究分析。若测得水平最大主应力和水平最小主应力的比值较大,如大于1.5,则地应力非均质性作用下使得割理角度对煤岩直井井壁稳定影响极大,割理角度α1在30°~45°时,井周煤岩块体易剪切滑落,导致井壁失稳,此种情况下不适合使用直井开采。可通过调整钻井设计案例,优化井眼轨迹,保持井壁相对稳定。同理,在确定水平井走向,达到沟通割理,获取煤层气通道的同时也需考虑割理角度的影响。

