基于正交试验的隧道近接施工隔离桩优化设计

王祖贤，施成华，陈刚

基于正交试验的隧道近接施工隔离桩优化设计

王祖贤1，施成华1，陈刚2

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 中交一公局集团有限公司，北京 100024)

隔离桩作为一种主要的施工控制措施广泛应用于隧道近接敏感建(构)筑物施工中，但目前尚未有规范对隔离桩的设计做出规定，现行隔离桩设计主要依据经验进行。针对这一现状，采用数值方法对影响隔离桩隔离效果的桩长、距隧道距离、桩径和桩弹模等4个主要因素进行正交试验，定义隔离系数并以此作为试验指标表征隔离桩隔离效果，分析评价各因素对隔离桩隔离效果的影响程度。研究结果表明：桩长是影响隔离桩隔离效果的最主要因素。进一步基于隔离桩影响因素评价对隔离桩合理桩长的确定进行设计优化，建议隔离桩桩长取1.2倍的隧底埋深时，能取得较好的隔离效果。

隔离桩；正交设计；优化设计；合理桩长

随着我国城市轨道交通建设的迅速发展，修建的轨道交通线路越来越多，所面临的施工环境也日益复杂，有更多的地铁线路敷设在老城区地下空间。由于修建年代较为久远，老城区建筑类型以浅基础砌体结构或浅基础低层框架结构为主，对地铁隧道施工引起的地层响应极为敏感，施工风险较高。因此，在邻近这些敏感建(构)筑物进行地下工程施工时，为确保施工安全，减小隧道或基坑施工引起的建筑物变形，极有必要采取一定的施工控制措施。针对地下工程施工引起的建筑物响应问题，国内外学者已经进行了广泛研究[1−6]。在目前的工程实践中，通常采用“变形源头控制、路径隔断及对象加固保护”[7]3种思路进行邻近敏感建(构)筑施工时的施工控制。其中隔离桩(墙)作为一种有效的地层变形路径隔断措施被广泛应用于工程实践中[8−18]，并取得了良好的施工效果。如上海外滩隧道在侧穿浦江酒店时，采用隔离桩作为保护措施后邻近隧道侧基础最大不均匀沉降由23 mm减小至7 mm[10]；济南轨道交通R1线小半径盾构隧道下穿京沪高铁桥时，采用隔离桩后桥桩沉降最大减幅达41.8%[13]。目前也有一些学者对隔离桩的作用机理及作用效果进行了研究[15−18]，纪新博等[8]针对某地铁新建隧道侧穿邻近浅基建筑采用隔离桩隔离的工程为依托，对隔离桩的桩长、桩间距和距隧道距离3个参数进行了敏感性分析，但在结果分析中采用极差作为因子敏感性评价指标缺乏一定的合理性。隔离桩作为地下构筑物，由于其隐蔽性，目前的研究主要是对现场施工措施的计算论证以及现场监测。对隔离桩的控制机理及计算模型的研究较为欠缺。此外，影响隔离桩控制效果的主要因素尚不明确，处于模糊的状态。尽管隔离桩在工程实践中得到了广泛应用，但在现行的设计规范中并未对隔离桩的设计做出相关规定，目前隔离桩的设计主要依据现场经验，因此其设计参数具有较大的不确定性。因此，有必要对隔离桩的设计参数进行研究，为之后的隔离桩设计提供依据。为此，本文基于隧道开挖对邻近建筑影响的某经典案例，采用数值方法建立计算模型，首先明确了影响隔离桩作用效果的主要因素并进行正交试验，定义了隔离系数并以此作为试验指标对隔离桩隔离效果进行分析评价，然后依据统计学中的方差分析对隔离桩主要参数进行了显著性检验。在此基础上对隔离桩合理桩长的确定进行设计优化。

1 数值模型

1.1 模型概况

Daniela等[4]采用有限元方法对一条形基础混凝土框架结构在邻近隧道开挖时的响应进行了研究，其所建立的隧道−建筑物分析模型具有一定的典型性。本文基于Daniela的研究，采用通用有限元软件Abaqus建立隧道−建筑物−隔离桩平面有限元模型，进行邻近敏感建筑物隧道开挖时隔离桩隔离效果分析及评价研究。计算模型中的岩土工程性质和隧道结构尺寸根据Fargnoli等[5, 19]的研究，参考意大利米兰地铁5号线确定。

图1 有限元计算模型

为完全消除边界效应的影响，模型在水平方向(方向)和深度方向(方向)分别取130 m和60 m。模型中隧道开挖直径为=6.7 m，埋深=15 m。地表建筑物为5层混凝土框架结构，层高3.2 m；柱截面尺寸为400 mm×400 mm，采用C35混凝土浇筑；梁截面尺寸为250 mm×250 mm，采用C30混凝土浇筑；基础为混凝土条形基础，混凝土强度等级为C35，基础长13.2 m，埋深1 m，基础距隧道中心线10 m。计算模型如图1所示。

1.2 模型边界及计算参数

模型边界采用位移边界，即分别约束模型水平方向和竖直方向的法向位移，地表为自由边界。计算时建筑物的梁和柱均采用梁单元(B21)模拟，其余部件均采用平面应变单元(CPE4)单元模拟。在材料本构关系的选择上，隔离桩及建筑物基础和结构均采用线弹性本构模型，土体采用Mohr-Coulomb理想弹塑性本构模型。模型计算参数如表1和表2所示。其中土体杨氏模量的取值参考米兰地铁5号线邻近工程土体小应变剪切刚度实测曲线确定，Daniela等根据实测曲线将地层分为6层，每层土体杨氏模量随深度非均匀增加，Daniela和Fargonli所采用的地层参数如图2所示。本文为便于计算，模型中取土体弹性模量随深度线性变化，这与Daniela等采用的值基本相符，其余土体参数的选取同Daniela的计算模型。

表 1 土体计算参数

1.3 接触关系及隧道开挖模拟

建筑物基础与土体以及隔离桩与土体之间的接触关系采用经典的Coulomb摩擦接触，摩擦因数根据界面摩擦角确定。对于桩土界面摩擦角的确定，一些学者，如Potyondy等[20−21]给出了估算公式，本文根据Daniela等[4]建议取混凝土−土界面摩擦角为=2/3。

表2 结构计算参数

图2 土体小应变剪切模量随深度变化曲线

隧道开挖模拟，其实质为地层应力释放。Abaqus提供了2种隧道开挖模拟方法，本文采用物理意义更为明确的收敛−约束法进行隧道开挖模拟。收敛−约束法实现隧道开挖引起的地层应力释放模拟原理为：在分析步中折减隧道周边单元的节点反力，该折减系数即为隧道开挖引起的应力释放系数。由于本文重点讨论隔离桩对隧道开挖引起的地层位移的隔离效应，因此隧道采用全断面一次性开挖。

1.4 模型验证

隧道开挖会引起地层损失，进而引起地层位移。在隧道开挖引起的地层位移预测方面，Peck[22]基于高斯分布函数建立的Peck公式广为应用。本文通过对比采用Peck公式和本文数值模型所得隧道开挖引起的地表横向沉降曲线的一致性来验证本文计算模型。图3所示为2种方法下所得地表横向沉降曲线。

由图3可知，采用本文数值模型所得的地表沉降曲线与采用Peck公式获得的地表沉降曲线具有较好的一致性。因此，在后续的计算分析中可采用本文所标定的数值模型。

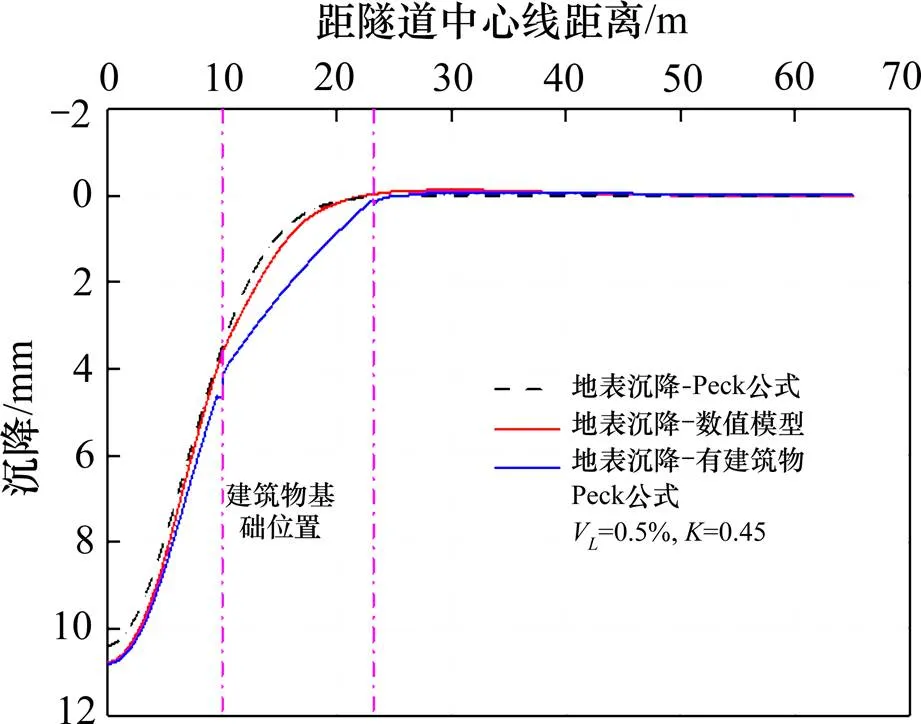
图 3 地表横向沉降曲线

2 隔离桩参数正交试验设计

2.1 隔离桩关键参数及试验指标确定

尽管隔离桩在实际工程中广泛应用，但在目前的规范中对隔离桩的设计无明确规定。根据纪新博等[8, 17]的研究工作，可见隔离桩桩长及隔离桩距隧道或边载作用距离是影响隔离桩隔离效应的主要参数。此外，翟杰群等[15]基于对隔离桩作用机理的研究，指出隔离桩“主要承受开挖施工引起的侧向土压力和地基差异沉降产生的摩阻力”。可见，在水平方向上在侧向土压力作用下，隔离桩的变形形式主要表现为弯曲变形，在荷载一定时桩的弯曲变形程度取决于桩的抗弯刚度(EI)，进而会影响到桩后地层的变形，因此桩的抗弯刚度也是隔离桩设计的主要参数之一。综上，本文以隔离桩桩长、隔离桩距隧道距离、桩身弹性模量以及桩直径作为隔离桩设计的主要参数进行正交试验设计。

尽管目前对于开挖引起的邻近建筑物响应问题已经有大量的研究，但还没有统一的评价指标去评定建筑物受影响程度。《城市轨道交通工程监测技术规范》将建筑物竖向位移和裂缝列为邻近地下工程施工时周边建筑物的应测项目，将倾斜和水平位移列为选测项目[23]，但在数值计算中因隧道施工引起的建筑物裂缝不易体现。另一方面，建筑物对地面均匀沉降并不敏感，造成建筑物破坏的主要原因是差异沉降，尤其砌体结构和低层框架结构对沉降差值更为敏感[24]，在实际施工中通常根据建筑物的差异沉降量推算出建筑物的倾斜值，并将建筑物倾斜列为应测项目。丁勇春[7]根据常见建筑的上部结构及基础形式，将建筑划分为以多层框架结构及高层结构为代表的刚性建筑和以砖混结构为代表的柔性建筑，并以建筑物倾斜值作为刚性建筑变形控制标准，对建筑的倾斜做了相关规定。本文研究的建筑物为低层框架结构，因此可将其划分为刚性建筑，以建筑的倾斜值作为隧道开挖下建筑物受影响程度的评价指标，可以综合反映隧道施工引起的建筑物响应特性。此外，由图3可知有浅基础时，地表沉降曲线在浅基础段也呈现出倾斜变形特性。另外，为评价隔离桩的隔离效果，定义隔离桩隔离系数为：

2.2 隔离桩参数正交试验设计

为保证样本具有较好的说服力，在进行数值试验时每个因素安排4个水平，因素水平的选择依据工程实际确定，选用L16(45)正交表安排数值试验。试验设计如表3和表4所示。

表3 试验因素及水平

表4 正交试验方案

3 隔离桩隔离效果评价

试验结果如图4所示。由图4可知，在这16组试验中，隔离桩隔离效果最为明显的是第15组试验，隔离系数=0.99，隔离效果最不理想的是第1组试验，隔离系数=0.24。此外，由图4可见，每4组试验之间的试验指标差异是较为明显的，但在每4组之内的差异不是特别显著。

图4 试验结果

根据试验结果，采用统计学中的方差分析方法对16组试验结果进行分析，鉴别各因素对试验结果的影响程度。方差分析表如表5所示，将各因子的值绘制在如图5所示的直方图中，进行各因子对试验结果影响水平显著性检验。

由图5可知，桩长的值远大于显著性水平=0.1时的临界值，而其余3个因子的值均小于临界值，因此可以认为对于隔离桩隔离效果影响最大的因素为隔离桩桩长，相对而言其他参数对隔离桩的隔离效果影响不明显，因此在进行隔离桩设计时应注重隔离桩桩长这一关键参数的确定。

表5 方差分析

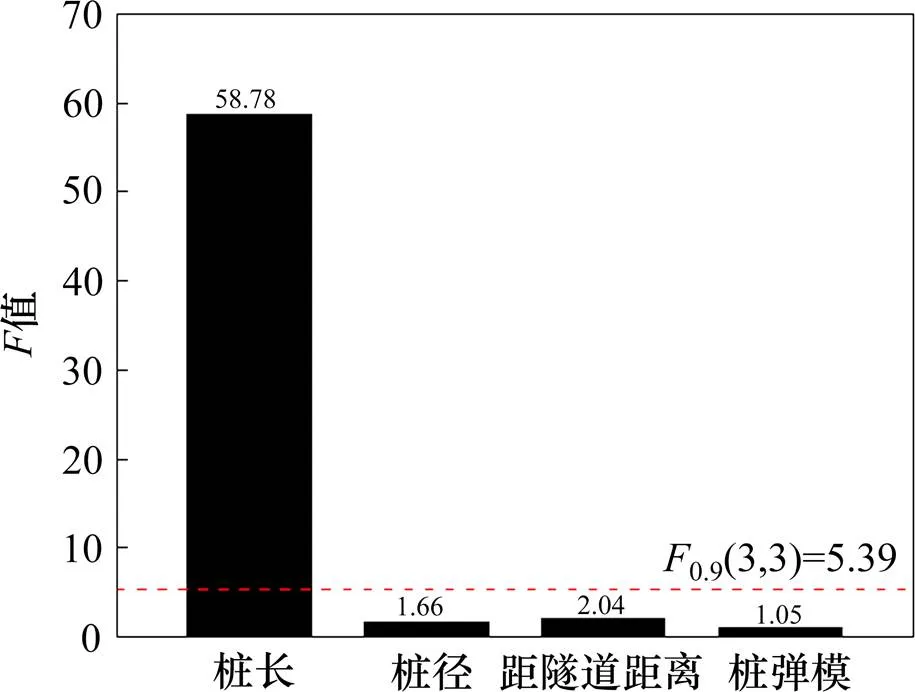
图5 各因子F值直方图

4 隔离桩设计优化

根据各因子显著性检验结果可知，桩长对隔离效果的影响是最为显著的，是隔离桩设计时的关键参数。但由图4可知，在桩长分别为22.5 m和30 m的这8组试验所得的隔离系数差异并不十分明显，相反，当桩长为22.5 m时所得的一些试验结果要优于桩长为30 m时的试验结果。可见当桩长达到一定长度之后隔离桩的隔离效应不会再有明显提升，同时，考虑桩的工程造价问题，桩长越长意味着更高的造价。因此在隔离桩设计时应使得隔离桩具有合理的桩长，这一长度应使得其能很好的起到隔离防护作用同时又不至于造成浪费，能够兼顾工程安全与经济。

翟杰群等[15]基于隔离桩控制基坑变形的机理分析，指出隔离桩的设置应穿过土体滑移面并具有一定的插入深度。卢致强等[12]建议隔离桩的嵌入深度应不小于4 m。然而在工程实践中，对于设计及施工人员而言，确定隧道开挖引起的土体潜在滑移面是一项较为繁杂的工作，他们更愿意接受更直观的设计方案。显然，相比于确定滑移面位置，隧道深度和洞径是更为直观的参数，同时根据工程经验，在进行隔离桩设计时，也会参考隧道的埋深进行相应的设计。

基于此，为确定隔离桩的合理桩长，本文定义隔离桩埋深比为：

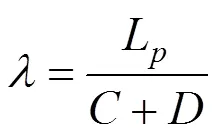
式中：L为隔离桩桩长，m；为隧道覆土厚度，m；为隧道直径，m。

本文基于前述数值模型，分别计算了隧道不同覆跨比(/)下采用不同长度隔离桩时的隔离效果，计算结果如图6所示。计算时隧道直径根据常见城市地铁隧道取=6.0 m。

图6 不同覆跨比及不同桩长下的隔离效果

由图6可见，为使隔离桩具有一定的隔离效果应至少取隔离桩埋深比≥1，即隔离桩应至少埋入至隧道底部。但随着隧道埋深的进一步增加，这一长度下的隔离桩并不能取得良好的隔离效果(＜0.8)。总体来看，当隔离桩埋深比达到1.2以上时，就能达到理想的隔离效果(>0.8)，能明显降低隧道开挖对邻近敏感建(构)筑物的影响，能有效保护邻近建(构)筑物。因此，本文基于大量的数值计算，建议在设计及施工时取隔离桩桩长为L=1.2(+)。

5 结论

1) 通过正交设计，对隔离桩桩长、距隧道距离、桩径及桩弹模4个主要的设计参数进行了4因素4水平的数值试验，对试验结果进行了方差分析和显著性检验，结果表明桩长是隔离桩最关键的参数，对隔离桩的隔离效果影响最为显著，相对而言其余3个参数对隔离效果的影响并不明显。

2) 根据因子影响水平的显著性检验结果对隔离桩的桩长设计进行了优化。计算了隧道不同覆跨比(/)下采用不同长度的隔离桩所得到的隔离系数，结果表明当隔离桩桩长取1.2倍的隧底埋深时，隔离系数>0.8，能达到良好的隔离效果，建议取隔离桩合理桩长为L=1.2(+)，其中为隧道覆土厚度，为隧道直径。

[1] 柳厚祥, 任志勇, 陈思宇. 隧道不同位置下穿施工引起邻近建筑物的变形分析[J]. 土木工程学报, 2014, 47(8): 128−137. LIU Houxiang, REN Zhiyong, CHEN Siyu. Deformation analysis of adjacent buildings due to the construction of undercrossing tunnel[J]. China Civil Engineering Journal, 2014, 47(8): 128−137.

[2] 任建喜, 李庆园, 郑赞赞, 等. 盾构诱发的地表及邻近建筑物变形规律研究[J]. 铁道工程学报, 2013(1): 69−74. REN Jianxi, LI Qingyuan, ZHENG Zanzan, et al. Research on the deformation laws of surface and adjacent building induced by shield tunnel[J]. Journal of Railway Engineering Society, 2013(1): 69−74.

[3] Farrell R, Mair R, Sciotti A, et al. Building response to tunnelling[J]. Soils and Foundations, 2014, 54(3): 269− 279.

[4] Daniela Boldini, Nunzio Losacco, Sara Bertolin, et al. Finite element modelling of tunnelling-induced displacements on framed structures[J]. Tunnelling and Underground Space Technology, 2018, 80: 222−231.

[5] Fargnoli V, Boldini D, Amorosi A. 3D numerical modelling of soil–structure interaction during EPB tunnelling[J]. Géotechnique, 2015, 65(1): 23−27.

[6] FU J, YU Z, WANG S, et al. Numerical analysis of framed building response to tunnelling induced ground movements[J]. Engineering Structures, 2018, 158: 43−66.

[7] 丁勇春. 软土地区深基坑施工引起的变形及控制研究[D]. 上海: 上海交通大学, 2009. DING Yongchun. Excavation-induced deformation and control in soft deposits[D]. Shanghai: Shanghai Jiaotong University, 2009.

[8] 纪新博, 赵文, 李慎刚, 等. 隔离桩在隧道侧穿邻近浅基建筑中的应用[J]. 东北大学学报(自然科学版), 2013, 34(1): 135−139. JI Xinbo, ZHAO Wen, LI Shengang, et al. Application of isolation piles on metro tunnel for side-crossing the buildings with shallow foundation[J]. Journal of Northeastern University (Natural Science), 2013, 34(1): 135−139.

[9] 曹伍富, 胡愈, 姚爱军, 等. 地铁隧道下穿建筑地基基础的灾变特征与控制[J]. 地下空间与工程学报, 2014, 10(增2): 2037−2042. CAO Wufu, HU Yu, YAO Aijun, et al. The catastrophe characteristic and control of metro tunnels passing though under building foundation[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(Suppl 2): 2037−2042.

[10] BAI Yun, YANG Zhihao, JIANG Zhiwei. Key protection techniques adopted and analysis of influence on adjacent buildings due to the Bund Tunnel construction[J]. Tunnelling and Underground Space Technology, 2014, 41: 24−34.

[11] 刘喆, 何平, 张安琪, 等. 盾构隧道施工过程及支护方式对高速铁路高架桥群桩基础影响分析[J]. 工程力学, 2016, 33(增1): 219−226. LIU Zhe, HE Ping, ZHANG Anqi, et al. Analysis of effects of shield tunnel construction process and supporting ways on pile groups of high-speed railway viaduct[J]. Engineering Mechanics, 2016, 33(Suppl 1): 219−226.

[12] 卢致强, 曹平, 刘建伟, 等. 地铁隧道侧穿邻近建筑中隔离桩的应用研究[J]. 铁道标准设计, 2016, 60(12): 97−102. LU Zhiqiang, CAO Ping, LIU Jianwei, et al. Study on application of shelter piles where subway tunnel passing sideway nearby buildings[J]. Railway Standard Design, 2016, 60(12): 97−102.

[13] 王国富, 郑涛, 路林海, 等. 小半径盾构下穿高铁桥支护优化及变形控制研究[J]. 防灾减灾工程学报, 2017, 37(1): 117−125. WANG Guofu, ZHENG Tao, LU Linhai, et al. Research on the optimization and deformation control of high speed railway bridge tunnel with small radius shield[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(1): 117−125.

[14] TANG J, LIU J Y, LIU Y. Study on the measures of tunnels side-crossing bridge based on sheltering effects of isolation piles[J]. IOP Conference Series: Earth and Environmental Science, 2017, 81: 012156.

[15] 翟杰群, 贾坚, 谢小林. 隔离桩在深基坑开挖保护相邻建筑中的应用[J]. 地下空间与工程学报, 2010, 6(1): 162−166. ZHAI Jiequn, JIA Jian, XIE Xiaolin. Practice of partition wall in the building protection projects near deep excavation[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(1): 162−166.

[16] 费纬. 隔离桩在紧邻浅基础建筑的深基坑工程变形控制中的应用[J]. 岩土工程学报, 2010(增1): 265−270. FEI Wei. Application of isolation piles to deformation control of deep foundation pits close to buildings with shallow foundation[J]. Chinese Journal of Geotechnical Engineering, 2010(Suppl 1): 265−270.

[17] 竺明星, 王磊, 龚维明. 边载作用下隔离桩隔离效果的影响因素研究[J]. 岩土工程学报, 2013, 36(4): 671−679. ZHU Mingxing, WANG Lei, GONG Weiming. Factors influencing isolation effects of isolation piles under side loading[J]. Chinese Journal of Geotechnical Engineering, 2013, 36(4): 671−679.

[18] 郑刚, 杜一鸣, 刁钰. 隔离桩对基坑外既有隧道变形控制的优化分析[J]. 岩石力学与工程学报, 2015(增1): 3499−3509. ZHENG Gang, DU Yiming, DIAO Yu. Optimzation analysis of efficiency of isolation piles in controlling the deformation of existing tunnels adjacent to deep excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015(Suppl 1): 3499−3509.

[19] Fargnoli V, Boldini D, Amorosi A. TBM tunnelling- induced settlements in coarse-grained soils: The case of the new Milan underground line 5[J]. Tunnelling and Underground Space Technology, 2013, 38: 336−347.

[20] Potyondy J G. Skin friction between various soils and construction materials[J]. Geotechnique, 1961, 11(4): 339−353.

[21] Randolph M F, Worth C P. Application of the failure state in undrained simple shear to the capacity of the driven piles[J]. Geotechnique,1981,11(4): 339−353.

[22] Peck R B. Deep excavations and tunneling in soft ground[C]// Proceedings of 7th international conference on soil mechanics and foundation engineering. Mexico City: State of the Art Report, 1969: 225−290.

[23] GB 50911—2013, 城市轨道交通工程监测技术规范[S]. GB 50911—2013, Code of monitoring measurements of urban rail transit engineering[S].

[24] Son M. The response of buildings to excavation-induced ground movements[D]. Urbana: University of Illinois at Urbana-Champaign, 2003.

Optimum design of isolation pile in tunnel close-spaced construction based on orthogonal test

WANG Zuxian1, SHI Chenghua1, CHEN Gang2

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. China First Highway Engineering Company Ltd, Beijing 100024, China)

As a main construction control measure, isolation piles are widely used in the construction of tunnel adjacent sensitive buildings. However, there is no specification for the design of isolation piles. The current design of isolation piles is mainly based on experience. In view of this situation, the orthogonal test was carried out for the four main factors affecting the isolation effect of isolation piles, which were the length of piles, the distance from tunnels, the diameter of piles and the elastic modulus of piles. The isolation coefficient was defined as an experimental index to characterize the isolation effect of isolation piles, and the influence degree of each factor on the isolation effect of isolation piles was analyzed and evaluated. The test results were analyzed by variance analysis and significance test. The results show that the length of the pile is the most important factor affecting the isolation effect of the isolation pile, while the other three factors have no significant impact on the isolation effect of the isolation pile. Based on the evaluation of the influencing factors of isolation piles, the reasonable length of isolation piles is optimized. It is suggested that the isolation effect is better when the length of isolation piles is 1.2 times of the depth of tunnel bottom.

isolation pile; orthogonal design; optimum design; reasonable pile length

10.19713/j.cnki.43−1423/u.T20190807

TU473

A

1672 − 7029(2020)07 − 1785 − 07

2019−09−10

国家重点研发计划资助项目(2017YFB1201204)

施成华(1973−)，男，安徽黄山人，教授，博士，从事隧道与地下工程方面的教学与科研工作；E−mail：csusch@163.com

(编辑 阳丽霞)