跨长江特大桥拉索涡激振动与风特性观测

刘宗杰，祝志文, 2，陈魏，陈政清

跨长江特大桥拉索涡激振动与风特性观测

刘宗杰1，祝志文1, 2，陈魏1，陈政清1

(1. 湖南大学 土木工程学院，湖南 长沙 410082；2. 汕头大学 土木与环境工程系，广东 汕头 515063)

为研究跨长江特大桥拉索风致振动的类别与风特性的关系，基于大桥健康检测系统和自开发的拉索振动监测系统，对荆岳长江大桥桥址风场特性进行监测，记录拉索振动数据并对拉索风致振动加速度与风场的相关性进行研究。研究结果表明：桥址平均风速的非平稳特性显著；随着风速增大湍流度逐渐减小。在低风速下，来流湍流强度较大，拉索振动随风速增大而增大；当风速增大时湍流强度逐渐减小，拉索振动加速度将减小；拉索振动可为平面内振动也可为平面外振动，为多模态风致涡激振动，且JB02号拉索在一定风速条件下面内振动与面外振动基本相同，当风速变化，可出现更高阶的振动。拉索面内涡激振动分段时程分析表明，拉索振动幅值增加，主导模态频率不改变，各模态振动幅值增加，但随风速的增大，拉索的涡激振动可在更高风速下被锁定，从而导致拉索发生更高阶的涡激振动。另外，湍流度小于40%时拉索振幅较大，湍流度增大拉索涡激振动加速度反而减小，且拉索的涡激振动只在特定的风向角下发生。

拉索；涡激振动；风特性；多模态；现场监测

斜拉索为斜拉桥的主要受力构件之一。主梁和桥面系恒载以及桥上活载大部分通过拉索传递到桥塔。斜拉索因长度大，易呈现刚度小和阻尼低的特点，容易在外部激励，如自然风作用下发生大幅度振动。斜拉桥工程实践表明，斜拉索的风致振动包括：涡激振动、尾流驰振、参数振动和风雨振 等[1]。涡激振动是拉索在常遇风速下发生的一种风致振动现象，其发生频次高，使得拉索本身尤其是其锚固系统或机械阻尼控制装置易发生长期的疲劳损伤，且拉索涡激振动还会使管养单位和桥面通行人员有不安全感，从而给桥梁正常运营带来隐患。Hikami等[2]在Meiko Nishi Bridge发现了斜拉索在雨水和风作用下引起的拉索振动，并且成功地在风洞中再现了类似的人工降水振动，同时指出，斜拉索也可以在没有降水的条件下由于拉索的轴向漩涡脱落而振动。Matsumoto等[3]通过风洞试验研究认为拉索的风致振动由涡激振动引起，并讨论了卡门漩涡在振动中的作用。ZUO等[4]对Fred Hartman大桥开展了现场实测，分析了拉索风雨激振和涡激振动的相似和不同之处。目前研究拉索风致振动的主要方法有风洞试验，现场实测和计算风工程等，而现场实测是研究风荷载和拉索风致振动最直接和最可靠的手段。本文以荆岳长江大桥为研究对象，基于大桥健康检测系统和自开发的拉索振动监测系统，对平均风速和风向、湍流度，以及拉索振动进行监测，通过记录拉索振动数据对拉索的多模态振动特性进行分析，并对拉索振动与风场相关性进行研究。

1 测量系统介绍

荆岳长江大桥是主跨为816 m混合梁斜拉桥，主梁采用分离式双边箱梁结构，中跨和北边跨采用扁平钢箱梁结构，南边跨采用PC箱梁结构，跨度组合为(100+298) m+816 m+(80+2×75) m。桥塔为双柱H形结构，南塔高224.5 m，北塔高267 m。斜拉索按扇形布置在竖直平面内，由208根斜拉索组成了平行双索面，每个索面由26对高强度平行钢丝斜拉索组成，全桥共4×26对，横桥向斜拉索索距为35 m，顺桥向标准梁段索距为15 m，北边跨尾索区标准索距为13 m。

如图1所示，在靠近北塔的JB01和JB02号拉索上安装双向加速度传感器，传感器安装高度为6.22 m，加速度传感器采样频率为100 Hz，量程为±2.5，测量精度为6 mg。同时在北塔和南塔的塔顶处安装超声风速仪，采样频率为1 Hz ，在跨中桥面处安装螺旋桨风速仪，实测数据通过桥梁健康监测系统进行传输。

2 桥址风场特性

荆岳长江大桥位于洞庭湖平原，属于Ⅰ类地貌，紊流强度较小，比较容易激发拉索的涡激振动，而对于位于峡谷中的桥梁，风容易受附近山体的干扰，紊流度往往比较大。本文选取2019年4月9号8点到4月10号8点的24 h风速数据，其10 min平均风速如图2所示，可见桥址风速的非平稳特性显著；南塔塔顶风速与北塔塔顶风速变化趋势以及风速大小基本一致，跨中桥面与塔顶风速的变化趋势保持一致。北塔塔顶最大风速超过17 m/s。

图1 主桥桥型布置图

图2 10 min平均风速时程曲线

图3为北塔塔顶处风速计给出的1 min时距湍流度随风速的变化，低风速时风中的脉动风成分占比较大，塔顶湍流度最大达到了0.56。且随着风速增大，湍流度逐渐减小，风速13 m/s时湍流度与规范值[5]接近，但增大风速湍流度进一步减小。

图4为北塔顶的风玫瑰图，可见北塔处主导风向为北风。由于桥址处的主导风向与桥梁纵桥向夹角较大，引起拉索的振动为横风向风振，风在拉索的两侧背后产生交替的漩涡，由一侧接着向另一侧脱落，形成卡门涡列，从而使拉索表面的风压呈周期性的变化，作用方向与风向垂直，交替涡流引起拉索的振动，并且当涡激脱落频率接近拉索的固有频率时，拉索将产生涡激共振[6]。

图3 北塔塔顶湍流度随风速变化

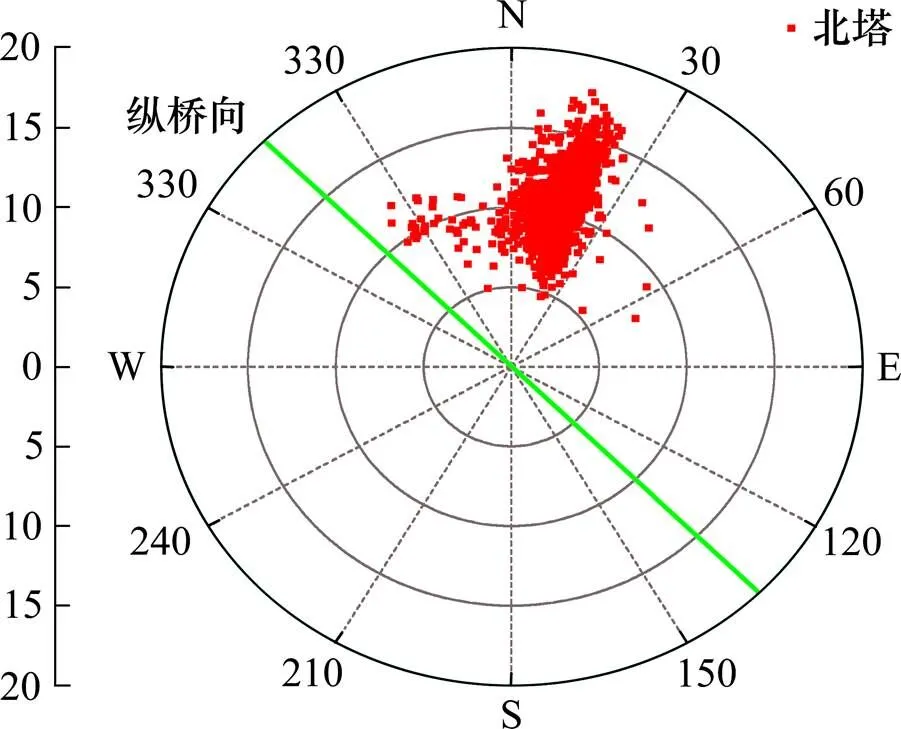
图4 塔顶风玫瑰图

3 拉索振动特性

在4月9日8点到15点时风速较大，拉索振动较为明显，故选取上述时段中8点到15点的数据进行分析，该时段JB01号拉索与JB02号拉索均有较为明显的振动，因此需要分析JB01号拉索以及JB02号拉索的振动特性。JB01号拉索长度为137.66 m，拉索直径为103 mm，倾斜角为82.4°，初始张力为2 066 kN，JB02号拉索长度为144.39 m，拉索直径为103 mm，倾斜角为77°，初始张力为1 735 kN，且JB01号拉索和JB02号拉索处没有设置外置阻尼器。

3.1 JB01号拉索振动分析

图5展示了JB01号拉索的加速度时程，可见面内加速度远大于面外加速度，最大的面内加速度为2.5，而对应时刻的面外加速度响应仅为0.5。拉索的振动加速度随着风速的变化而显著变化。

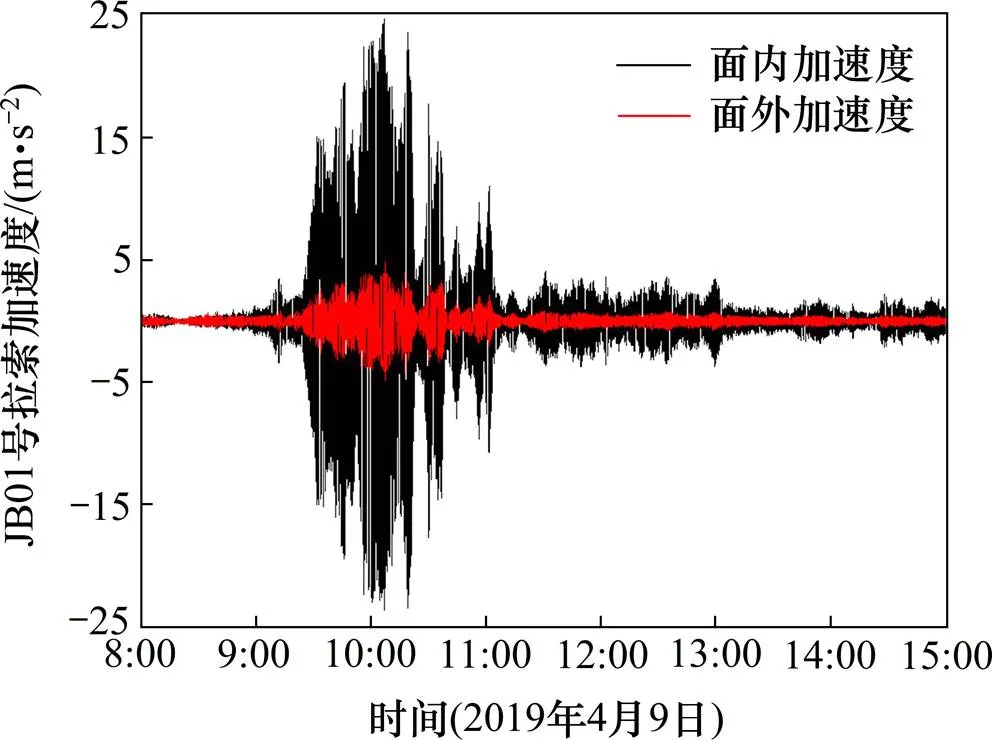
图5 JB01索加速度时程

图6展示了JB01号拉索在风荷载激励下1 min的面内加速度均方根值与1 min面外加速度的均方根值的关系，可以看出面内加速度与面外加速度有明显的线性关系，面内加速度约为面外加速度的5.6倍。因此，在后续分析中仅分析JB01号拉索的面内振动。

取4月9日10点拉索振动较大处5 min数据进行频谱分析，可得到频谱图如图7所示，拉索振动为高阶多模态振动，这种现象出现的原因是平均风速在边界层随着高度的增加，而斯托罗哈数与平均风速呈线性关系，因此对于一根倾斜的拉索，可以沿着拉索轴线的不同高度处以不同的模态频率锁定涡流脱落[7]，而塔顶风速与桥面平均风速之比为1.4，这使得JB01号拉索振动可能出现多种模态。此外，由图7可以看出，相邻2阶模态频率之差为0.99 Hz，也即JB01号拉索的基频，该时程的主导频率为11.81，12.8和13.82 Hz，分布在11~14 Hz之间，分别对应拉索的第12，13和14阶模态。由于拉索的振动不是以单一模态频率振动，因此在拉索减震设计时需要进行多模态振动的减震，对于JB01号拉索，只需控制其面内振动即可。

图6 JB01索加速度时程

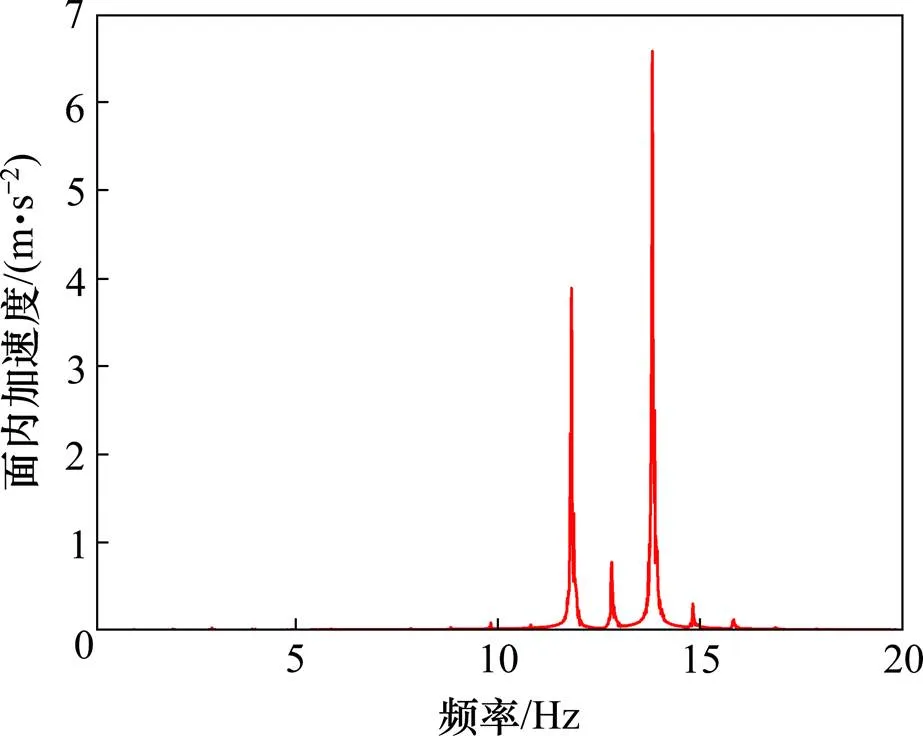
图7 面内加速度时程频谱图

在风荷载作用下，拉索的振动响应不是单调增加或者单调减小，拉索的加速度时程曲线由很多响应段组成，为了解拉索在不同时间的响应特性，取其中典型响应段进行分析。图8为9点20分开始的900 s的加速度实测曲线图，这段时间内拉索振动加速度较大，面内加速度最大值达到了1.5。如图所示，0~300 s拉索振动幅度最小，加速度均方根为0.13，桥面平均风速为9.5 m/s。300~600 s拉索振动幅度逐渐增大，这段时间加速度均方根为0.48，桥面平均风速为8.5 m/s。600~900 s拉索振动幅度相对较大，加速度均方根为0.95，桥面平均风速为9.2 m/s。

图8 9:20起900 s加速度时程

图9~11分别为归一化后加速度频谱图随时间的变化。图9为9点20分开始300 s，可以看出，该响应段为高阶多模态振动，主导频率为 11.77 Hz和12.74 Hz，对应着拉索的第12阶和第13阶模态，并且主导频率没有随时间而发生明显变化。图10为14点40分开始第300~600 s，主导频率为 11.77 Hz，这段时间内拉索振动加速度逐渐增加，可以看出主导模态的振动幅度也是随时间逐渐增加。图11为14点40分开始第600~900 s，主导频率为11.77 Hz，这段时间拉索振动加速度增加到1.5后保持稳定，可以看出拉索的振动模态阶数没有变化，主导模态的振动幅值较为稳定。

图12为10点左右加速度响应最大时的3 s时程曲线，基于测量的加速度响应数据，为估计拉索的位移响应模态分量[8]，假设拉索的振动加速度响应可以由个分量的形式近似表示为：

其中：a为拉索的加速度响应；Ai为第i个加速度响应的模态分量；ωi为第i个模态的角速度频率；φi为第i个模态的相位角。

图10 300~600 s加速度时程频谱图

图11 600~900 s加速度时程频谱图

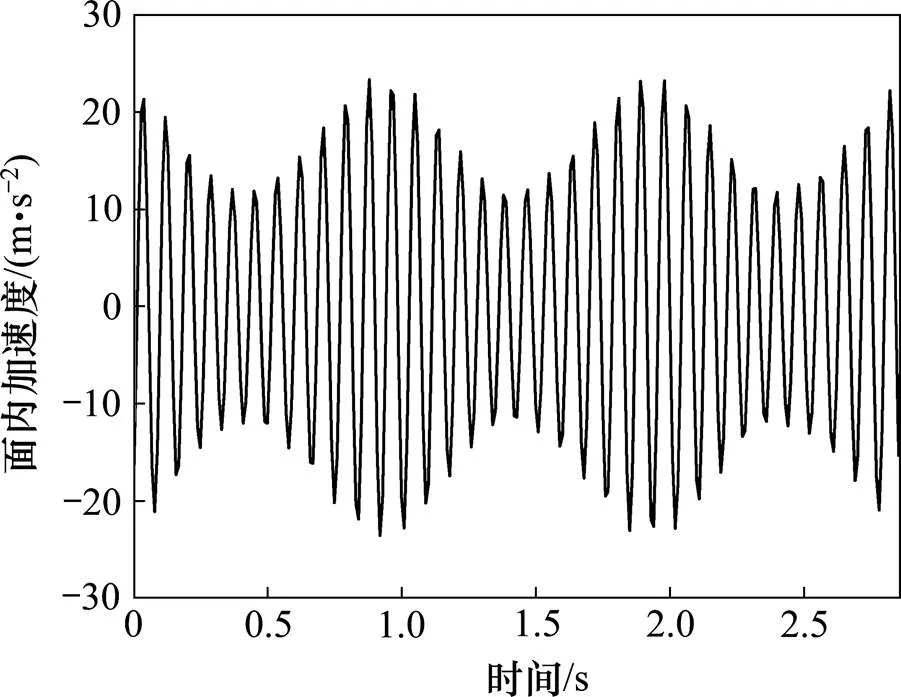
图12 3 s加速度时程曲线段

拉索的振动最大的3 s内，拉索的振动主要由第12阶，第13阶以及第14阶模态引起，因此加速度响应可以通过这3阶模态比较好的拟合。其中ω已知，而A与φ可以通过曲线拟合得到。由此可得到拉索加速度响应的拟合曲线，如图13所示，实测数据与拟合数据之间有良好的一致性。借助理论性状的模态组合，估计拉索在测量点出的位移响应模态分量如图14所示，第12阶，第14阶模态贡献了绝大部分的位移响应。

图13 实测加速度时程曲线与拟合曲线

3.2 JB02号拉索振动分析

图15为JB02号拉索8点到15点的加速度时程，图16展示了JB02号拉索在风荷载激励下1 min的面内加速度均方根值与1 min面外加速度的均方根值的关系，在11点40分之前，面内加速度与面外加速度基本相等，在11点40分之后，面内加速度为面外加速度的3.04倍，因此后续的分析中需要对拉索的面内振动与面外振动均进行分析。

图14 拉索位移响应

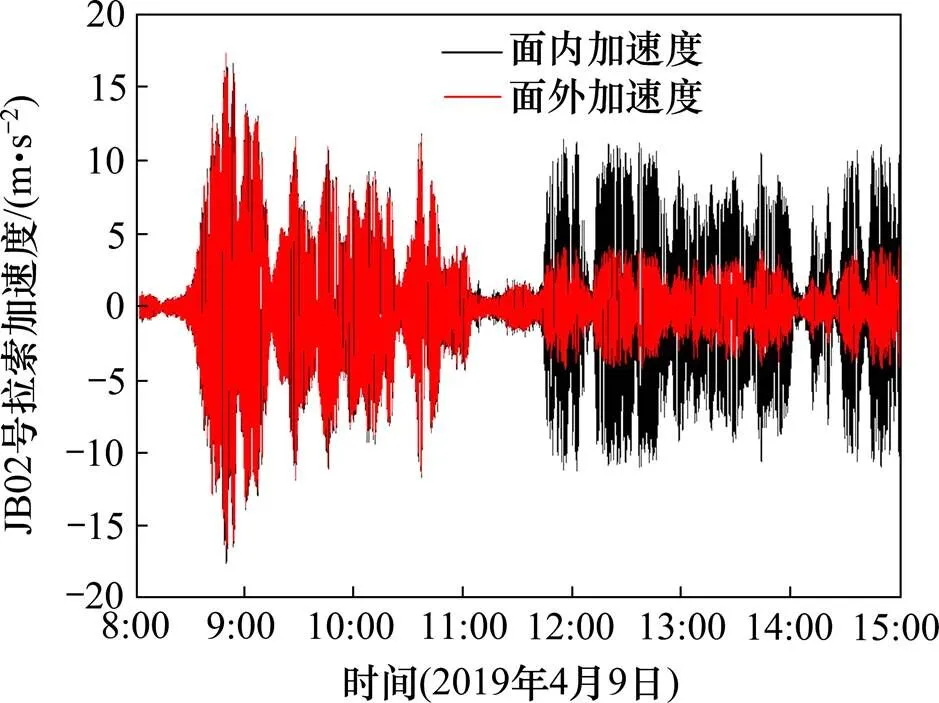
图15 JB02索加速度时程

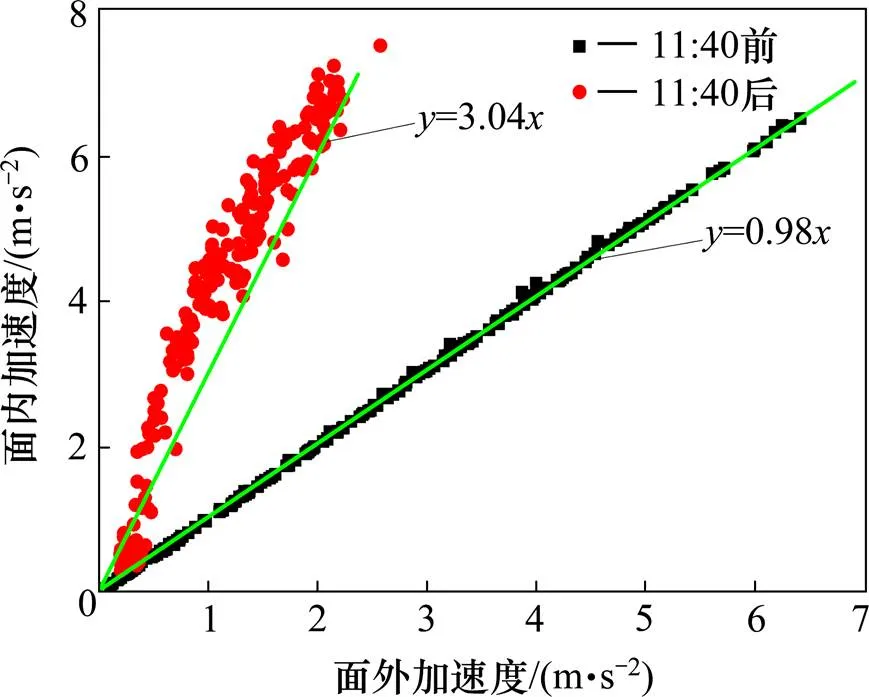
图16 JB02索加速度时程

图17 加速度时程频谱图

对JB02号拉索进行分析，取8点50分振动最大处进行频谱分析，可得到JB02号拉索面内以及面外振动频谱图如图17所示，此时JB02拉索此时的面内振动模态与面外振动模态基本一致。JB02号拉索的振动基频为0.89 Hz，面内振动以及面外振动主导频率均为13.15，14.04和14.93 Hz，分布在13~15 Hz之间，分别对应拉索的第15，16和17阶模态。

JB02号拉索在11点44分之后面内加速度远大于面外加速度，对其变化前后5 min的面内振动与面外振动分别进行频谱分析。如图18和图19所示，在加速度变化的过程中，拉索的面内振动与面外振动的主导模态以及模态转移情况保持一致，在11点44分前，JB02号拉索的面内振动与面外振动的主导频率均为17.84 Hz，为第20阶模态，在11点44分后，拉索的模态发生了转移，JB02号拉索的面内振动与面外主导频率最终稳定在25.4 Hz，为第28阶模态。在主导模态变化的相近时间段内，风速增大，导致其主导模态发生了明显的改变，由多阶高模态振动变为了单阶高模态振动，且面内面外的主导模态频率保持一致。由图15中JB02拉索的加速度时程曲线可知，其在11点左右，加速度有明显的减小，在此后的44 min内面内与面外加速度较小但面内加速度与面外加速度仍然基本保持一致，在11点44分时，面内加速度以及面外加速度均突然增大且面内加速度远大于面外加速度，这是由于风速增大，导致拉索涡激振动的涡激力也增大，同时涡旋脱落的频率也增大，而导致斜拉索在11点43分在频率25.4 Hz产生了涡激振动，导致了拉索更高阶的振动。

图18 面内加速度时程频谱图

图19 面外加速度时程频谱图

对于JB02号拉索在整个过程中，其拉索的主导频率由8点50分时的12~15 Hz变为了11点44分的25 Hz，拉索的锁定频率发生了较大的变化。由于此时来风方向与拉索夹角为35°~45°之间，因此引起的拉索振动为垂直风向也即与拉索平面的面内以及面外均有振动。对于JB01以及JB02号拉索，由于其特性的不同，而导致了2根拉索面内外振动响应不同，JB01号拉索振动以面内振动为主，JB02号拉索既会出现面内振动也会出现面外振动。在拉索涡激振动的控制中，往往忽略了拉索的面外振动，而实际上在风荷载作用下，拉索也会产生较大的面外涡激振动，对桥梁结构造成破坏，影响拉索的使用寿命。

4 拉索振动特性

图20为JB01与JB02拉索振动加速度随桥面平均风速的变化，图20表明，JB01拉索的振动是受风速所限制的，拉索的振动加速度随着平均风速增大，风速位于7~11 m/s时拉索的振幅最大，当风速小于13 m/s时，风的湍流强度远大于规范值，因此更容易引起拉索的振动。JB02号拉索振动，由于主导频率较高，因此振动加速度相比JB01号拉索振动加速度较小，且JB02号拉索在风速位于8~18 m/s之间时拉索振幅最大。涡激振动是一种较低风速下发生的有限振幅振动，同时涡激振动只有在某一风速区间内发生[9]，JB01号以及JB02号拉索的振动满足涡激振动的振动特征。

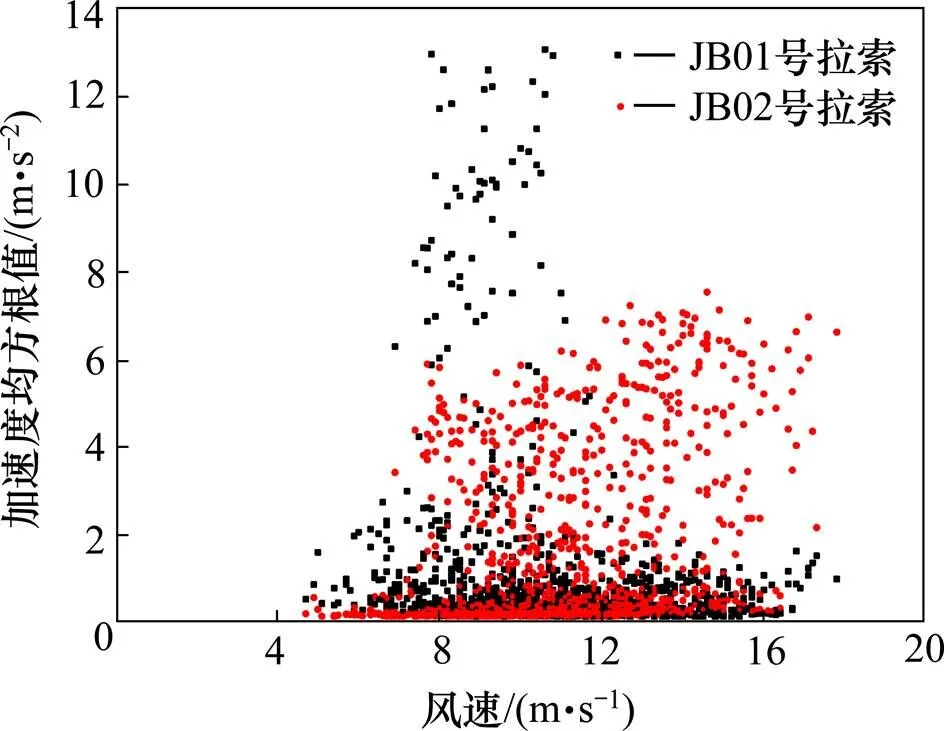
图20 拉索振动幅值随平均风速变化

图21为拉索振动加速度随北塔塔顶风湍流度的变化，图21表明，拉索振动主要发生在湍流度小于40%的范围内，当湍流度大于0.4之后振动幅值明显减小。因此拉索的振动在一定的风速范围内，且来流湍流强度较小时，拉索的振动幅值最大[10]。

图22为JB01号拉索和JB02号拉索振动加速度随风向角的变化，图22结果表明，斜拉索的振动幅值与风向角具有较大的相关性。当来流与桥轴向成60度或者240度附近时，JB01拉索振动幅度最大，当来流与桥轴向成60度或者120度附近时，JB02拉索振动幅度最大。在其他风向角下，拉索的振动幅度相对较小。拉索振动时来流风向并不垂直于桥轴向，因此拉索发生面内振动的同时也伴随着面外振动。

图21 拉索振动幅值随湍流度变化

图22 拉索振动幅值随风向角变化

5 结论

1) 桥址风速的非平稳特性显著，低风速下塔顶湍流度较大，随着风速增大，湍流度逐渐减小，低风速下较大的湍流度导致拉索大幅度振动。

2) 拉索振动可为平面内振动也可为平面外振动，为多模态风致涡激振动，且JB02号拉索在一定风速条件下面内振动与面外振动基本相同，当风速变化，可出现更高阶的振动。

3) 拉索在振动时为高阶多模态涡激振动，拉索振动幅值增大，主导模态频率不变，但是各模态振动幅值增大。但随风速的增大，拉索的涡激振动可在更高风速下被锁定，从而导致拉索发生更高阶的涡激振动。

4) 拉索振动随风速增大，湍流度小于40%时拉索振幅较大，湍流度增大对拉索涡激振动起抑制作用，拉索振动减小。并且拉索只在特定的风向角情况下出现大幅度的涡激振动，其他风向角下，拉索的振动幅度较小。

[1] 储彤. 某大跨度斜拉桥风场与斜拉索涡激振动现场监测研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. CHU Tong. In-situ monitoring investigfations for wind field and vortex-induced vibrations of stayed cables in a large-span cable stayed bridge[D]. Harbin: Harbin Institute of Technology, 2013.

[2] Hikami Y, Shiraishi N. Rain-wind induced vibrations of cables stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1−3): 409−418.

[3] Matsumoto M, Shiraishi N, Shirato H. Rain-wind induced vibration of cables of cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1−3): 2011−2022.

[4] ZUO D, Jones N P, Main J A. Field observation of vortex-and rain-wind-induced stay-cable vibrations in a three-dimensional environment[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6−7): 1124−1133.

[5] GB 50009—2012, 建筑结构荷载规范[S]. GB 50009—2012, Load code for the design of building structures[S].

[6] Matsumoto M, Yagi T, Shigemura Y, et al. Vortex-induced cable vibration of cable-stayed bridges at high reduced wind velocity[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(7−8): 633−647.

[7] NI Y Q, WANG X Y, CHEN Z Q, et al. Field observations of rain-wind-induced cable vibration in cable-stayed Dongting Lake Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(5): 303−328.

[8] Jan Ming Ko, CHEN Z Q, NI Yiqing. Field vibration tests of bridge stay cables incorporated with magneto rheological (MR) dampers[J]. Proc Spie, 2002, 4696: 30− 40.

[9] 王修勇, 陈政清, 倪一清, 等. 环境激励下斜拉桥拉索的振动观测研究[J]. 振动与冲击, 2006(2): 138−144, 191. WANG Xiuyong, CHEN Zhengqing, NI Yiqing, et al. Response characteristics of stay cable under ambient excitation[J]. Journal of Vibration and Shock, 2006(2): 138−144, 191.

[10] CHENG S, Irwin P A, Tanaka H. Experimental study on the wind-induced vibration of a dry inclined cable—Part II: Proposed mechanisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(12): 2254−2272.

Observation of vortex-induced vibration and wind characteristics of cables across the Yangtze river bridge

LIU Zongjie1, ZHU Zhiwen1, 2, CHEN Wei1, CHEN Zhengqing1

(1. College of Civil Engineering, Hunan University, Changsha 410082, China; 2. Department of Civil and Environment Engineering, Shantou University, Shantou 515063, China)

In order to study the relationship between the wind-induced vibration type of the cable across the Yangtze River Bridge and the wind characteristics, based on the bridge health detection system and the self-developed cable vibration monitoring system, the wind field characteristics of the Jingyue Yangtze River Bridge site were monitored and recorded. The cable vibration data was studied and the correlation between wind-induced vibration acceleration and wind field was studied. The research shows that the average wind speed of the bridge site is not stable. With the increase of wind speed, the turbulence gradually decreases. At low wind speed, the incoming turbulence intensity is large, and the cable vibration increases with the wind speed increase. When the wind speed increases, the turbulent flow intensity decreases gradually, and the cable vibration acceleration will decrease. The vibration of the cable can be in-plane vibration or out-of-plane vibration. It is multi-modal wind-induced vortex-induced vibration, and the in place-vibration of JB02 cable under the certain wind speed condition is basically the same as the out-of-plane vibration. When the wind speed changes, it can appear higher order vibration. The time-history analysis of the vortex-induced vibration in the cable plane shows that the vibration amplitude of the cable increases, the dominant mode frequency does not change, and the amplitude of each mode vibration increases. However, as the wind speed increases, the vortex of the cable increases. Vibration can be locked at higher wind speeds, resulting in higher order vortex-induced vibrations of the cable. In addition, when the turbulence is less than 40%, the amplitude of the cable is large, and the turbulence increases, and the vortex acceleration of the cable decreases, and the vortex-induced vibration of the cable occurs only at a specific wind direction angle.

cable; vortex induced vibration; wind characteristics; multi-modality; on-site monitoring

10.19713/j.cnki.43−1423/u.T20190834

U441+.4

A

1672 − 7029(2020)07 − 1760 − 09

2019−09−17

国家重点基础研究发展计划(“973”计划)资助项目(2015CB057701)；国家自然科学基金资助项目(51878269)；湖南省研究生创新资助项目(521293361)

祝志文(1968−)，男，湖南益阳人，教授，博士，从事工程结构抗风研究；E−mail：zhuzw@stu.edu.cn

(编辑 涂鹏)