Scratch绘制美妙函数曲线

白二娃

不知你还记得百岁山有个美少女给路边老头送水的广告吗？是不是不明所以？其实这个广告讲述的是一个“笛卡尔曲线”的爱情故事。

1649年18岁的瑞典公主克里斯汀在斯德哥尔摩的街头邂逅了52岁穷困潦倒的数学家笛卡尔。闲谈后，公主聘请笛卡尔成为自己的数学老师，教授她研究数学的新领域——直角坐标系。两人在教学中彼此产生爱慕之心，这事被国王知道后下令流放笛卡尔，软禁克里斯汀。笛卡尔直到去世依然坚持写信给公主，可惜这些信都被国王拦截了。笛卡尔去世前的最后一封信中写了一个特殊的方程式r=a（1-sinθ），因为没人能看懂国王就把这封信给了公主。公主解开这个方程式得到了一个心形曲线，也知道了笛卡尔的心意，这就是著名的“笛卡尔曲线”（图1）。

我们根据一些简单的函数方程式就可以绘制出美妙的曲线，但是在计算机没有普及的时候，绘制函数曲线是很复杂的工作（图2）。

1. 函数的概念

数学中“函数”的定义：给定一个数集A，假设其中的元素为x。现对A中的元素x施加对应法则f，记作f（x），得到另一数集B。假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示。我们把这个关系式就叫函数关系式，简称函数。函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

编程中的函数也有类似但不完全相同的概念，其中函数的输入参数可以看作是定义域A，函数的运行所改变的结果可以看作值域B，而函数的算法（过程）就是对应法则f。

Scratch里我们可以在“自制积木→制作新的积木”里建立新函数。

2. 函数曲线

在二维平面，如果有函数 f（x） = y，其中任意一组（x，y）值是该曲线上的点的横坐标和纵坐标值，描绘出符合函数的全部点时可以在平面直角坐标系上呈现为一条曲线。

要想掌握使用Scratch根据各种不同的函数方程式绘制曲线的通用方法，我们要从最基础的一次函数开始，逐步掌握更加复杂的曲线绘制方法，画出各种优美的函数曲线图形感受数学之美。

3. 一次函数

若两个变量x，y间的关系式可以表示为y=kx+b（k，b为常数，k≠0）的形式，则称y是x的一次函数（x为自变量，y为因变量）。

我们先从最简单的一次函数y=x开始。x是横坐标，y是纵坐标。y=x函数的意思就是横坐标和纵坐标的值永远一样，即：

x=1 时 y=1 …… x=100 时 y=100

在Scratch里，我们就可以画100个纵横坐标相等的点，把它们连起来就是y=x的函数曲线，一根从（0，0）开始的向（1，1）的直线（图3）。

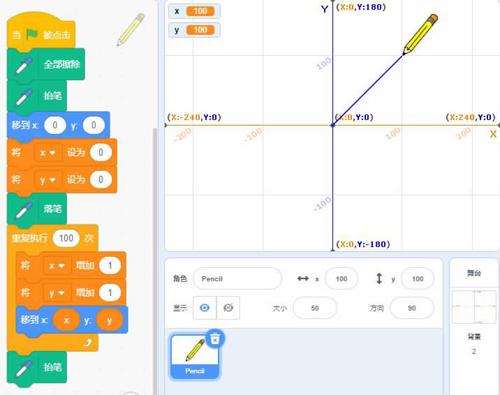
我们之后再增加两个变量k、b，并改变函数，就可以画出任意一次函数y=kx+b的曲線。为了更好地 规范和简化代码，我们将画图和函数部分分开了，为函数新建了积木“一次函数‘k‘b‘x”，这个积木有3个数字参数。这样每次计算y=kx+b时，只需要拖动这个积木到需要的地方就可以了。

而要改变函数内部结构时，也只需要修改一次函数的定义部分就可以了，函数越复杂就越能节省开发时间并避免出错。

4. 二次函数

二次函数基本表示形式为y=ax2+bx+c（abc为常量，a≠0）。 二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。x2用x*x表示。a、b、c可以自己设置，x从-50增加到50（图4、图5）。

5. 正弦曲线

接下来我们画一些和三角函数相关的曲线。Scratch里有三角函数积木，运算→“绝对值”积木下拉菜单中可以选择使用。

正弦曲线函数可表示为y=Asin（ωx+φ）+k，其中sin为正弦符号，A、k、ω和φ是常数（A、k、ω、φ∈R，R是实数域即A、k、ω、φ均为实数，且ω≠0），正弦曲线是一条波浪线。只需要根据函数设定和修改相应积木即可。具体常数设置如图7。

6. 椭圆形和圆形

椭圆的+=1，其中a>0，b>0，当a=b时就是正圆形。将这个公式转为参数方程方便计算xy的值：x=acosθy=bcosθ，θ为角度，画图时用循环代码重复360次，将θ从0度增加到360度，a、b为常量控制椭圆的外形，代码如图8，图9，效果如图10。

7. 笛卡尔曲线

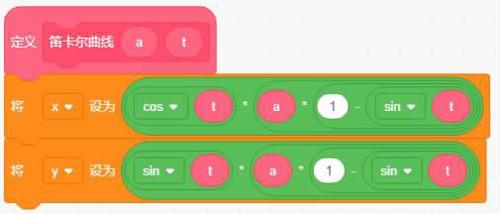
最后我们来画笛卡尔曲线。我们已知的r=a（1-sinθ）是笛卡尔曲线的极坐标公式，没有x和y坐标，需要转为直角坐标，变成下面的函数：

x=cos t*a（1-sint）

y=sin t*a（1-sint）

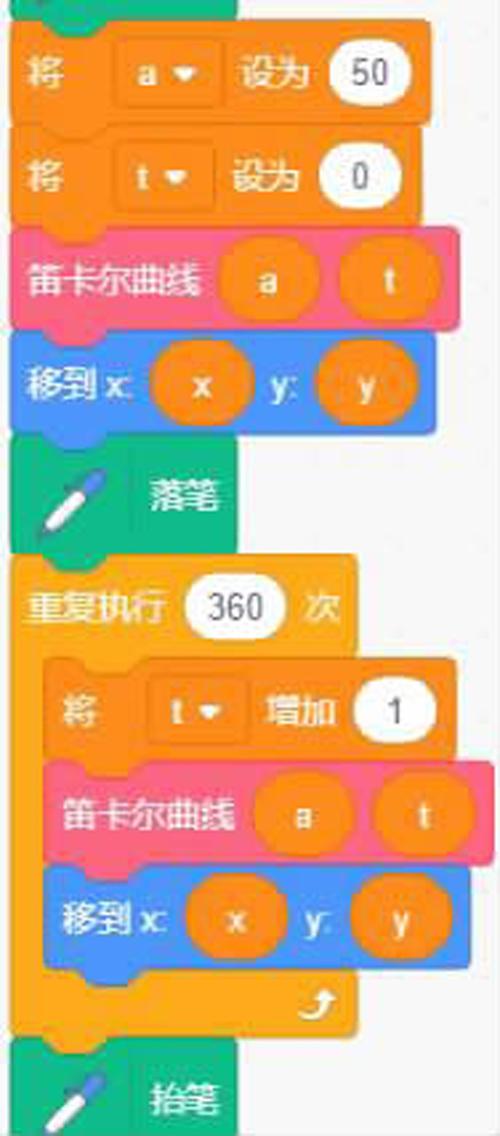
其中a是控制心形大小的常量。t为角度参数，通过Scratch编程让画笔跟随t转一圈即从0度-360度就可完成作画，代码如图11，图12，效果如图2。

8. 其他曲线效果

只要知道曲线函数的表达公式你可以用此种方法画出各种美丽的图形，搜索“proe曲线方程”可以找到几十种漂亮的曲线方程。当你有更多的数学知识就可以把这些公式轉化为程序画出来了，因为其中有不少曲线需要纵坐标z，这要用公式将（x，y，z）坐标转换为当前视角（xz，yz）的坐标才能画出来。再添加上变换颜色的代码，整个图形就非常漂亮了。

在本版扫码下载中有一个莫比乌斯环3D源程序（@科技传播坊），你可以下载后自行学习如何换算z坐标（如图13）。

9. 总结

根据函数公式画曲线，首先需要找到曲线的直角坐标系公式，如果是极坐标公式需要提前转换，这样才可确定曲线上点的x和y坐标。接着根据公式设定相应变量，并在新建积木中组合好x和y的表达方程式。循环给自变量x赋值，根据方程式算出因变量y的值，让画笔循环在（x，y）画点就可以画出相应的曲线了。

如果是有sin、cos等三角函数相关曲线，一般需要将角度变量变化360次（一个圆周）。