递推数列求通项新视角
2020-08-06 11:57:32高召
高中数学教与学 2020年13期
高 召
(河南省三门峡市第一高级中学,472000)
满足an+1=an(n∈N*)的数列{an}为常数列,其通项公式为an=a1(n∈N*).由递推关系求数列的通项公式时,若能把递推关系转化为an+1=an的形式,就可以通过常数列这个新视角使问题得以简便快捷的解决.
一、an+1=pan+An+B(p≠0, 1, A2+B2≠0)型递推数列
例1已知数列{an}中,a1=2,an+1=4an+3n+2,求{an}的通项公式.
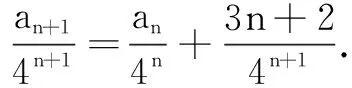
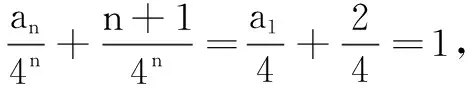
评注对an+1=pan+An+B(p≠0, 1,A2+B2≠0)型递推数列,两边同除以pn+1,再由待定系数法,同理可得数列{an}的通项公式.
二、an+1=pan+Aqn(pqA≠0, p≠q)型递推数列
例2已知数列{an}中,a1=1,an+1=2an+3n,求{an}的通项公式.
解将an+1=2an+3n两边同除以2n+1,
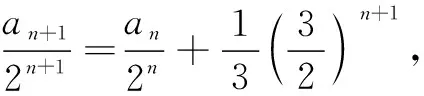



an=3n-2n(n∈N*).
评注上述解法不难推广到an+1=pan+Aqn(pqA≠0,p≠q)型递推数列.
三、an+1=f(n)an+g(n)(f(n)≠0)型递推数列.
例3已知数列{an}中,a1=1,nan+1=(n+2)an+n,求{an}的通项公式.
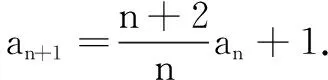
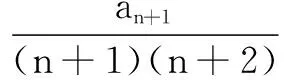


=1,
得an=n2(n∈N*).
评注更一般地,对an+1=f(n)an+g(n)(f(n)≠0)型递推数列,可通过如下类似的方法构造常数列,使通项公式轻松获得.

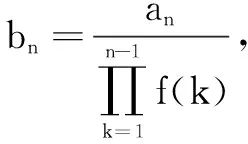
bn+1=bn+h(n).
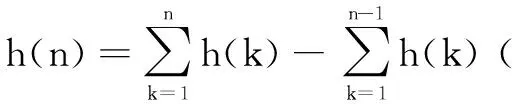
综上可见,对于符合以上几种情形的递推数列,都可以通过巧妙构造常数列的方法,简便快捷地求出其通项公式.
猜你喜欢
数理天地(高中版)(2022年19期)2022-05-30 10:48:04
新世纪智能(数学备考)(2020年11期)2021-01-04 00:38:16
郑州大学学报(理学版)(2020年1期)2020-02-08 08:40:00
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27 20:09:58
Chinese Medical Sciences Journal(2019年1期)2019-04-11 09:26:46
当代贵州(2018年21期)2018-08-29 00:47:16
高中生·天天向上(2016年3期)2016-05-05 03:06:38
都市丽人(2015年5期)2015-03-20 13:33:30
都市丽人(2015年4期)2015-03-20 13:32:58
中学生数理化·教与学(2014年10期)2014-10-22 02:19:04

