多维光纤通信系统性能监测技术

蒋 林，易安林，盘 艳，闫连山，潘 炜，罗 斌

西南交通大学信息光子与通信研究中心，成都611756

随着智能世界的到来，物联网、人工智能、大数据、云计算、5G 等多种新兴技术为用户带来了极致的体验，同时也使网络数据流量呈现爆发式增长趋势. 为满足海量数据的传输需求，将新型多维复用技术与多维调制格式相结合，能实现超高速、大容量光纤传输系统的目标，但随之而来的是系统对链路中各种线性损伤以及非线性损伤的容忍度急剧下降，致使系统的传输性能和传输可靠性严重降低[1]. 此外，“宽带中国”和“一带一路”等国家战略的实施，加快了中国及沿线各国信息基础设施（海底/陆地光缆）建设的速度. 光信号在链路传输过程中会受到由光纤、放大器、网络节点器件等引入的链路内部损伤，也可能受到由山体滑坡、雷击、地震以及第3 方有意挖掘破坏光缆等引入的链路外部损伤，这些情况都将严重影响正常的通信传输，大大降低通信传输质量（quality of transmission, QoT）乃至造成网络通信服务中断[2]. 因此，为保障光纤传送网能安全可靠地运行，需要对光纤传输系统中多个关键链路参量进行监测. 对于未来体系架构更为复杂的光纤传送网，采用性能监测技术具有以下优点：1）为网络管理系统提供信息来源和管理依据；2）有效诊断信号劣化来源，为损伤补偿提供反馈信息；3）实时反映光网络物理状况，为QoT 评估提供数据参考；4）动态辅助网络控制层，实现链路物理资源优化配置.

光纤传送网架构如图1 所示，信号从源节点A经历多个中间节点B/E传输到目的节点F.在传输过程中，信号会受到多种链路内外损伤效应的影响，其中包括色散效应（chromatic dispersion, CD）、非线性损伤、光信噪比（optical signal noise ratio, OSNR）、调制格式（modulation format, MF）、偏振模色散（polarization mode dispersion, PMD）、偏振相关损耗（polarization dependent loss, PDL）、放大器自发辐射（amplifier spontaneous emission,ASE）噪声、比特率（bit rate, BR）、非法入侵事件等. 这些损伤参量是目前影响系统性能的关键性因素. 在多维光纤通信系统中，借助性能监测技术实现链路多种损伤参量的监测与预警将具有重要意义. 目前，性能监测方面的研究工作主要集中在单个损伤参量监测以及少数损伤参量的联合监测. 为保障未来动态的、结构复杂的、受多种损伤参量影响的光纤传送网安全运行，性能监测技术将朝着精细化、一体化、多参量联合监测方向发展. 本文旨在总结性能监测技术的研究现状，并将重点讨论色散参量监测、非线性参量监测、调制格式参量监测等技术的研究现状和经典案例，随后讨论并分析多维光纤通信系统性能监测技术的发展趋势.

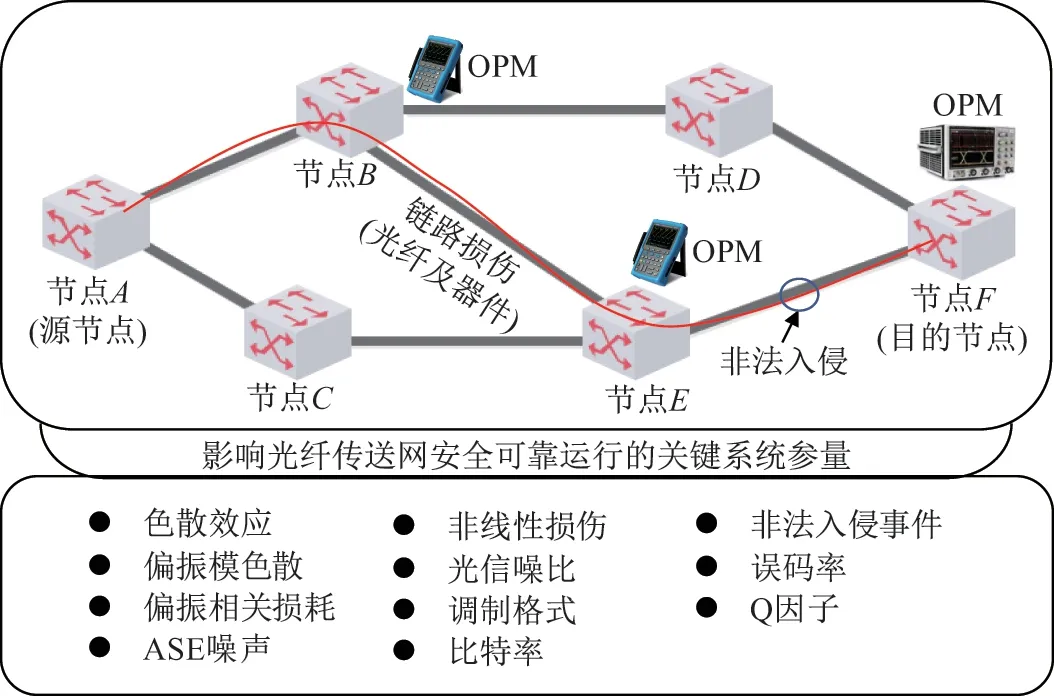
图1 光纤传送网中影响系统性能的几个关键参量Figure 1 Several key parameters affecting system performance in optical fiber transmission network

1 色散参量监测技术

1.1 色散参量监测技术研究进展

信号在光纤传输过程中，会因累积色散效应而造成码间串扰，这将严重影响传输信号的质量. 在光纤传输系统的接收端对累积色散效应进行监测与均衡，将对信号优化解调起到关键性作用. 目前，色散补偿主要采用光学色散补偿和数字域色散补偿两种方法. 光学色散补偿方法利用色散补偿光纤[3]和啁啾光纤光栅[4]产生反向色散效应，补偿传输信号在标准单模光纤中受到的累积色散，其主要缺点是需要在线插入色散补偿光纤和啁啾光纤光栅，在一定程度上增加了系统插入损耗与链路复杂度. 但对于链路累积色散出现变化的情况，光学色散补偿方法很难进行动态精准补偿. 数字域色散补偿方法可以不改变原有的传输系统，而在接收端采用数字信号处理技术对由色散效应所引起的信号畸变进行补偿与均衡，在很大程度上降低了传输系统成本. 此外，针对链路累积色散出现变化的情况，可在接收端通过色散参量监测算法对链路累积色散值进行实时精准监测与均衡.

近年来，多个科研团队在色散参量精准监测方面开展了很多有意义的研究工作. 其中，慕尼黑联邦军事学院课题组[6]提出一种基于Godard’s 误差标准的色散参量监测方案. 该方案需要预设一个较大范围的色散表，并以一定色散步长执行查表补偿色散操作，随后监测补偿以后信号的Godard’s 误差值，最终获取最优的链路累积色散值. 澳大利亚墨尔本大学课题组提出一种基于数据辅助的色散参量监测方案. 该方案需要在发射端提前添加训练序列，在接收端通过已知的训练序列实现传输信道估计，随后以最小均方拟合法获取相位响应，最终实现色散参量监测功能. 香港理工大学课题组[7]提出一种基于自相关功率波形的色散监测方案. 该方案可通过监测信号自相关功率波形的峰值位置，最终推算出链路累积色散值. 美国贝尔实验室课题组[8]提出一种针对单载波系统的峰均值功率比色散监测方案，该方案同样需要预设一个较大范围的色散表，随后执行查表色散补偿操作，最后通过监测信号峰均值功率比来实现链路累积色散监测. 西南交通大学课题组[9]提出一种基于两级粗细自适应色散监测方案，以时域与频域相结合的监测方式实现链路累积色散的复杂度低且精度高的监测. 华中科技大学课题组[10]提出一种基于分数阶傅里叶变换的色散监测方案，该方案根据不同链路累积色散值呈现不同分数阶傅里叶变换特征的情况，推算出对应的链路累积色散值. 北京邮电大学课题组[11]提出一种基于深度神经网络的链路累积色散监测方案，将低速率采样以后的数字信号送入神经网络进行训练，然后根据训练模型监测链路累积色散值. 本文总结了各种色散参量监测方案的技术特点，如表1 所示；随后将基于两级粗细自适应色散监测方案作为色散参量监测案例，详细分析该方案的工作原理和实验结果.

1.2 色散参量监测案例——基于两级粗细自适应色散监测方案

1.2.1 工作原理

本小节将详细分析基于两级粗细的自适应色散监测技术[9]，具体研究方案包括两级色散监测结构：粗色散监测模块和精细色散监测模块. 本方案的色散监测原理如图2 所示，接收端数字信号Ein[n]进入第1 级粗色散监测模块，获取链路累积色散的粗估计值. 该色散监测模块

表1 色散参量监测技术方案总结Table 1 Summary for chromatic dispersion monitoring schemes

使用Wiener-Khintchine 定理[7]的自相关方程来衡量链路累积色散，可定义为

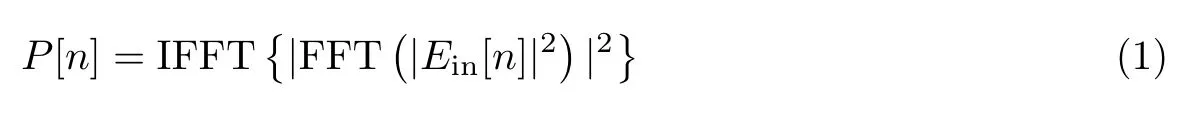
式中，FFT 和IFFT 为傅里叶变换和逆傅里叶变换. 当传输信号为NRZ 脉冲形状时，根据式(1)计算出的自相关峰值较小，且使用峰值推算累积色散值也将变得较为困难. 为解决这一问题，本文对数字信号Ein[n]采用延时相减操作，该操作可实现高通滤波的作用，将有效提升自相关波形的峰值高度，更利于本方案通过峰值来监测所对应的累积色散值. 因此，式(1)可重新定义为

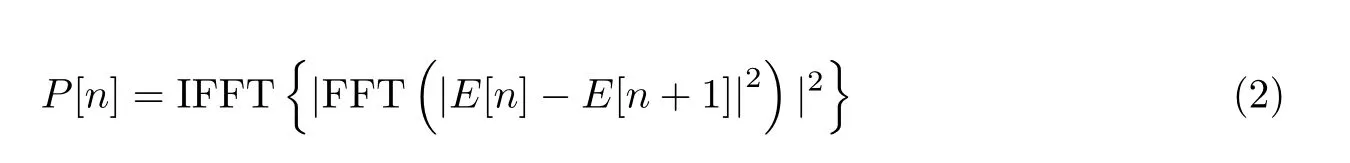
式中，自相关功率波形P[n]的峰值位置τ可定义为

式中，T0为高斯脉冲宽度，β2为群速度色散因子，z为光纤传输长度，T为符号周期. 在长距离传输系统中，(T0)2β2z，则式(3)可进一步简化. 此外，链路累积色散可表示为

式中，c表示光在光纤中的传输速度，λ表示光载波波长. 根据式(4)可知累积色散值对符号速率比较敏感. 例如，当符号率为10 GBaud 时，色散监测分辨率δres为624 ps/nm，即监测的色散误差最大可能为624 ps/nm. 当符号速率为25 GBaud 时，色散监测的分辨率可降低到100 ps/nm，最大监测误差也有一定程度的下降. 根据上面分析可知，第1 级粗色散监测模块误差仍然相对较大，需要使用第2 级精细色散监测方法进一步减小监测误差以获取高精度色散监测值. 本方案将以第1 级色散粗估计值δestc为中心，以色散监测分辨率δres（大约几百ps/nm 的色散值）为范围，建立一个色散区间表[δestc−δres，δestc+δres]. 采用一个小色散步长扫描色散区间表，均衡信号色散损伤效应，并监测Godard’s 误差值的大小. 最小的Godard’s 误差对应的色散即为精准色散监测值.

图2 色散参量监测方案原理图Figure 2 Diagram of chromatic dispersion monitoring scheme

1.2.2 结果分析

符号率为10 GBaud/s 的传输系统所对应的不同色散方案监测结果如图3(a)所示，符号率为28 GBaud/s 的传输系统所对应的不同色散监测方案结果如图3(b)所示. 不同色散监测方案包括基于自相关功率波形的色散监测方案[7]（图中标识为ACSPW algorithm），以及本小节方案（图中标识为FCMA algorithm）. 两种符号率传输系统的OSNR、差分群时延（differential group delay, DGD）、PDL 分别设置为14 dB、15 ps、15 dB. 根据原理部分的分析可知，在10 GBaud 传输系统中，ACSPW 算法的色散监测分辨率为624 ps/nm，即最大色散监测误差为624 ps/nm. 从图3(a)中以可发现，ACSPW 算法在光纤长度大约为40 km 范围内的色散监测值都相同，即色散监测误差约为600 ps/nm，因此该方案无法适用于低速率传输系统. 从图3(b)中可以发现，FCMA 算法具有约为40 ps/nm 的色散监测误差，因此有能力应用在实际系统中. 在28 GBaud 传输系统中，ACSPW 算法的色散监测分辨率（最大色散监测误差）约为80 ps/nm，相对于10 GBaud 传输系统的色散监测分辨率已经有所减小，但监测误差仍然较大. FCMA 算法的色散监测误差可保持在40 ps/nm 以下，该方案色散监测误差的大小主要与FCMA 算法的第2 级色散步长、DGD、PDL、OSNR 等相关损伤的影响有关. 如果取更小步长值将可能得到更好的估计结果，但是步长值取得越小，复杂度则越大. 在实际系统中，需要整体权衡时间复杂度与色散监测精度之间的关系. 另外，系统的DGD、PDL 较大时也会降低传输信号质量，以致影响色散监测性能. 接下来，将进一步分析各种损伤效应对本方案色散监测精度的影响.

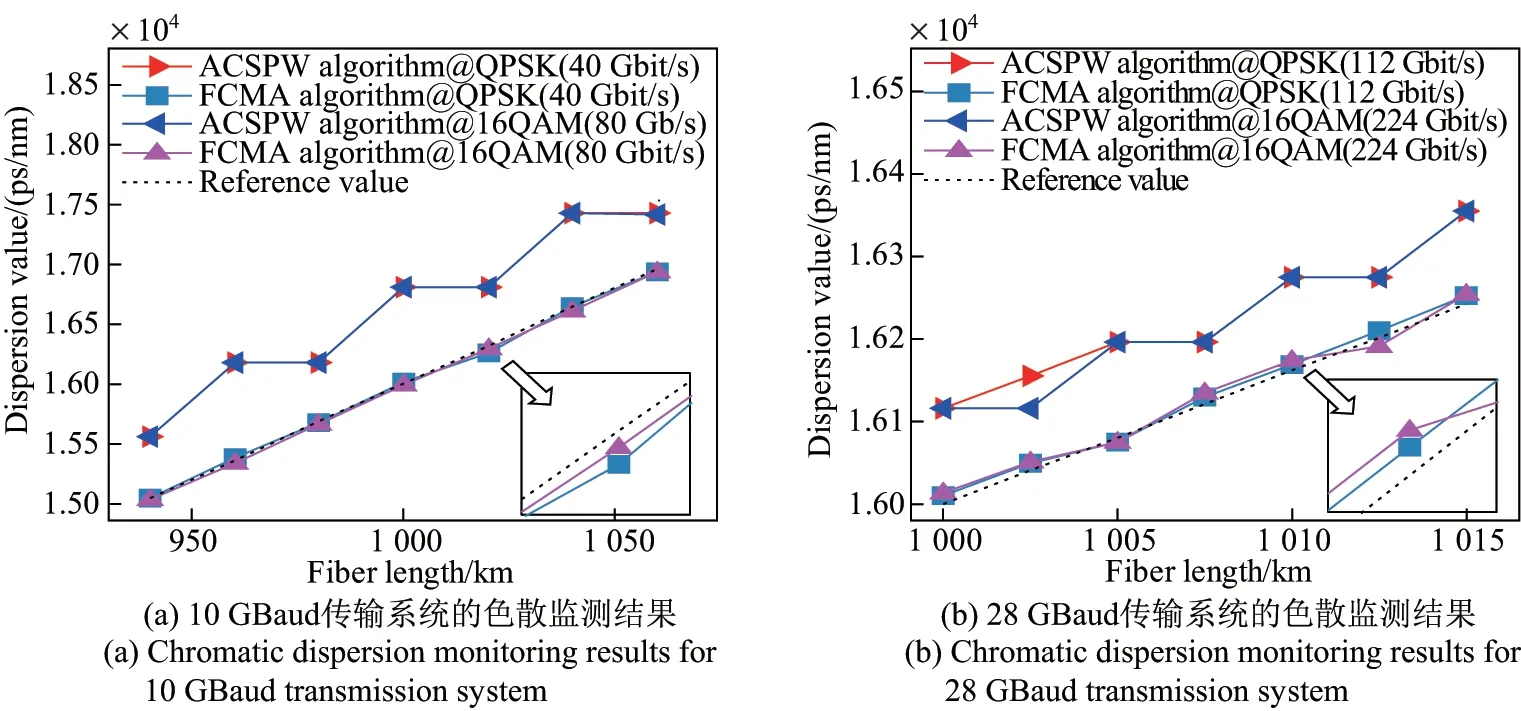
图3 不同符号率传输系统所对应的色散监测结果Figure 3 Chromatic dispersion monitoring results under different symbol rates

系统传输距离与OSNR 分别设置为1 000 km 和14 dB. 本方案在不同PDL（0～25 dB）与DGD（10 ps 和15 ps）条件下的色散监测误差如图4(a)所示. 当DGD 为10 ps 时，色散监测误差均小于15 ps/nm. 当DGD 提升到15 ps 时，色散监测误差均小于40 ps/nm.由此可看出，本小节方案对PDL 损伤效应不敏感，但DGD 将会造成色散监测精度下降.为进一步研究DGD 对FCMA 方案的影响，本小节测试了不同DGD（0～25 ps）与OSNR（14 dB 和20 dB）条件下的色散监测误差. 可从图4(b)中发现，当DGD 低于10 ps 时，色散监测误差保持在5 ps/nm 左右，相对恒定；当DGD 值大于10 ps 时，色散监测误差开始增大.主要原因是较大的DGD 值将严重损伤传输信号性能. 在通常情况下，典型偏振模色散的参量值约为0.1 ps/km0.5. 若要传输系统的DGD 值达到10 ps，光信号需要在传输系统中传输大约上万公里，由此可知本小节色散监测方案可适用于长距离光纤传输系统.

图4 不同损伤参量对色散监测结果的影响Figure 4 Influence of different impairment parameters on chromatic dispersion monitoring results

2 非线性参量监测技术

2.1 非线性参量监测技术研究进展

在超高速、大容量、超长距离的光纤通信系统中，光纤非线性效应已经成为系统传输容量和性能提升的主要障碍之一. 光纤非线性效应主要包括自相位调制、交叉相位调制、四波混频、受激拉曼散射以及受激布里渊散射等. 为实现长距离大容量光纤传输，研究人员主要采用大有效面积光纤[12]、抗非线性调制格式[13]、相位共轭[14]以及数字域非线性补偿算法[16-21]等对非线性效应进行抑制与均衡，其中大有效面积光纤和抗非线性调制格式通常可与其他方案一起联合使用. 在未来动态的长距离大容量传输链路中，如何精准地监测与补偿链路非线性效应，将是研究人员急需解决的关键问题之一. 在所提出的非线性均衡方案中，数字后向传输（digital backward propagation, DBP）算法是迄今为止研究最为广泛的非线性均衡技术.该方案需要提前预知传输链路中多个相关参数，并通过求解非线性薛定谔方程实现非线性补偿. 在实际传输系统中，光纤制造工艺不一致以及链路节点功率波动等因素都将影响链路信息的精确获取，以致无法实现优化的非线性补偿.

近年来，研究人员在非线性自适应监测方面开展了一定的研究工作. 德国埃尔朗根-纽伦堡大学课题组[22]提出了一种基于相位噪声方差的自适应非线性监测方案，该方案不断改变DBP 补偿过程中的非线性因子，同时监测载波相位恢复算法以后信号的相位噪声方差大小. 一旦获取最小相位噪声方差即可得到对应的非线性因子——最优化因子. 西南交通大学课题组[23]提出一种基于强度噪声方差的非线性监测方案，监测偏振解复用以后信号的强度噪声方差，进而根据强度噪声方差大小推导出最优化的非线性因子. 该方案可实现与文献[22]相同的监测精度但复杂度相对较低. 随后，该课题组进一步研究了一种基于Godard’s 误差的非线性监测方案，可实现接收端功率、非线性因子以及非线性补偿参数等多个非线性补偿相关参量的监测[24]. 麦吉尔大学课题组[25]提出基于相位噪声方差，实现了非线性因子与滤波器带宽的监测. 本文将各种非线性参量监测方案的技术特点总结如表2 所示，随后以基于强度噪声方差的非线性参量监测方案为非线性参量监测案例，详细分析该方案的工作原理和实现结果.

表2 非线性参量监测技术方案总结Table 2 Summary for nonlinearity parameter monitoring schemes

2.2 非线性参量监测案例——基于强度噪声方差的非线性参量监测技术

2.2.1 工作原理

相干接收机端的数字信号处理模块如图5(a)所示. 接收端所获取的模拟电信号通过模数转换器（analog to digital converter, ADC）转换为数字信号. 随后，数字信号通过本小节所提出的非线性参量监测与均衡方案（adaptive digital backward propagation, ADBP）来实现色散与非线性效应的补偿.补偿之后的信号再通过偏振解复用算法（polarization demultiplexing,PDM-DEMUL）实现解复用操作. 随后，通过频偏补偿算法（frequency offset compensation,FOC）以及载波相位恢复算法（carrier phase recovery, CPR）实现频偏补偿与载波相位恢复操作.

本小节所提方案原理如图5(b)所示，采用偏振解复用算法以后的信号来计算强度噪声方差CF=σ2[δI(nT)]，其中强度噪声波动δI(nT)可定义为

式中，Ed(nT)为偏振解复用之后的信号，T为符号间隔，n为数据点数目，为功率信号平均值. 在光纤传输链路中，光信号需要经历多段单模光纤与多段掺铒光纤放大器（erbium doped fiber amplifier, EDFA）. 在信号传输过程中，自相位调制效应将部分强度噪声转换为相位噪声. 因此，强度噪声与相位噪声将呈现一定的相关性，所对应的相位噪声方差也将与强度噪声方差呈现一定的比例关系. 相比于相位噪声方差评估信号质量，强度噪声方差也可作为一个有效度量来评估信号质量. 当信号质量变差时，可观察到强度噪声方差变大. 在监测过程中，本小节方案可直接判断信号强度噪声方差是否达到最小，以实现非线性相关参量监测. 如果强度噪声方差没有达到最小，该方案将以最小梯度更新规则不断更新非线性优化参量γξ，更新规则如下：

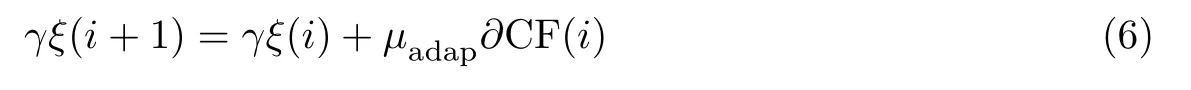
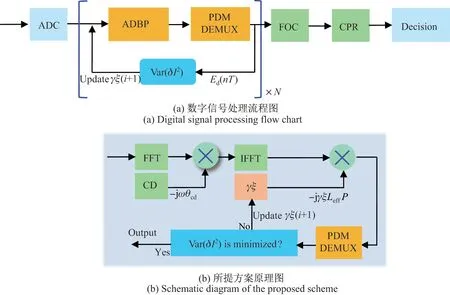
图5 所提方案实现过程Figure 5 Implementation process of the proposed scheme

式中，γξ(i)表示优化乘积γξ，∂CF(i)表示循环i次以后强度噪声方差的斜率，γ和ξ分别代表非线性参量和非线性补偿参数，收敛速度因子µadap为0.01. 强度噪声方差斜率可定义为

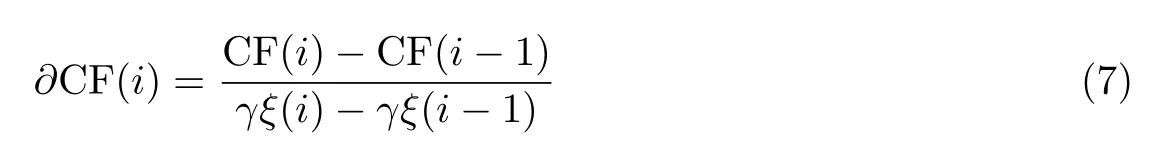
当强度噪声方差的斜率∂CF(i)点出现正负变化时，判断强度噪声方差是否达到最小，一旦获得优化的非线性参量γξ即可停止更新就最小梯度算法. 将优化的非线性参量γξ通过非线性补偿器进行补偿，其中非线性补偿器可定义为

式中，P表示色散补偿之后的信号功率.

2.2.2 结果分析

为验证本方案可行性，我们搭建了40/112Gbit/s 偏振复用（polarization division multiplexing, PDM）正交相移键控（quadrature phase shift keying, QPSK）和224 Gbit/s PDM-16 正交幅度调制（quadrature amplitude modulation, QAM）相干光传输系统进行仿真验证.40 Gbit/s PDM-QPSK 传输系统在720 km 光纤传输距离条件下的仿真结果如图6 所示. 在考虑不同接收端功率以及不同非线性相关参量乘积的条件下，计算出所对应的归一化强度噪声方差. 本小节的非线性参量监测算法可假设接收端功率为任意大小的值，通过监测强度噪声方差来获取最优化的非线性参量乘积. 不同的强度噪声方差对应图左边不同的星座图，代表不同的信号质量. 当强度噪声方差较大时，星座点iii 较为模糊，由此推测信号的非线性补偿效果较差，此时的非线性乘积参数并非最优；当强度噪声方差较小时，星座点i 较为清晰，此时所使用的非线性乘积参数是该系统中最优的.

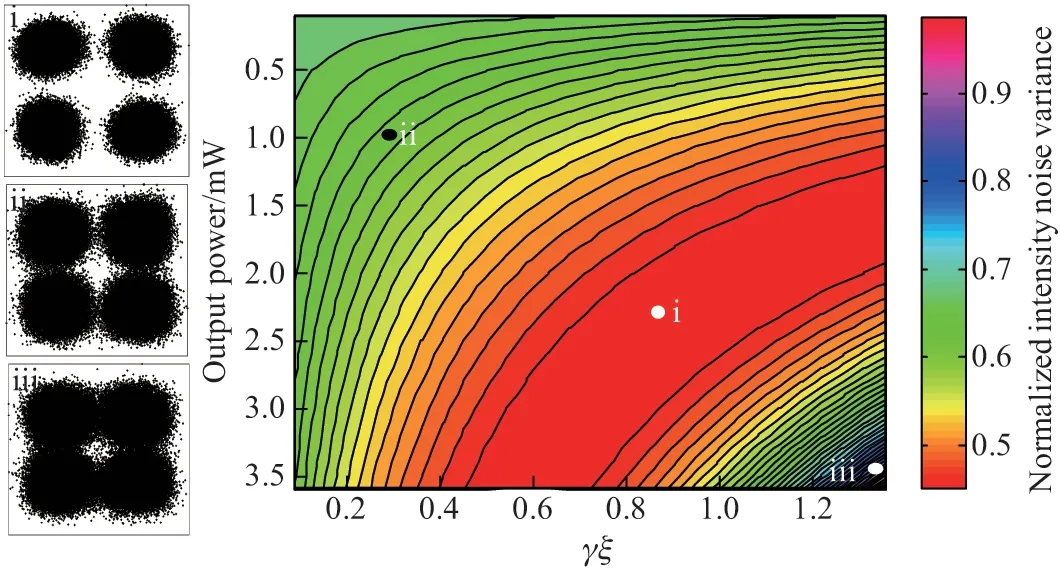
图6 不同非线性乘积条件下的归一化强度噪声方差Figure 6 Normalized intensity noise variance under different nonlinearity product

本小节方案（proposed method）、基于相位噪声方差的非线性损伤监测与均衡方案（previous method）、传统DBP 非线性补偿方案、线性均衡方案（linear equalization, LE）的补偿结果如图7 所示. 由于长距离传输链路中信号存在非线性损伤，在只考虑线性均衡的情况下，系统性能从整体上来说不如其他两种非线性损伤监测与均衡方案. 传统DBP 非线性补偿算法需要提前预知传输链路中的非线性相关参量，因此本小节选择乘积因子γξ为2.1 作为对比. 从图7 中发现，乘积因子为2.1 的传统DBP 非线性补偿算法实现的补偿性能，比LE 线性均衡方案的情况还差. 主要是因为不精准的非线性补偿将导致过补偿或者欠补偿，致使信号质量进一步下降. 相比于基于相位噪声方差的方案，本小节所提方案在监测性能和均衡性能方面与基于相位噪声方差的方案相当，但是本方案在非线性监测过程中不需要频偏补偿以及载波相位恢复算法，可在一定程度上减小复杂度.

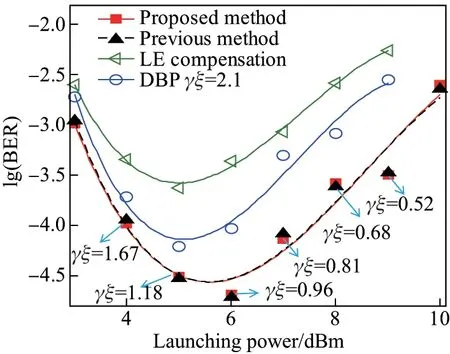
图7 各种非线性补偿方案的BER 结果Figure 7 BER results of various nonlinear compensation schemes

3 调制格式参量监测技术

3.1 调制格式参量监测技术研究进展

下一代弹性光网络将根据不同链路条件和服务质量动态地改变发射端调制格式、符号率、前向纠错编码等参数[26]，其调制格式等相关参数信息在其他网络节点的接收端处不确定. 然而，接收端有部分数字信号处理算法与调制格式相关，因此需要根据调制格式信息选择相应的最优解调算法[27]. 此外，调制格式信息对于中间网络节点的光性能监测设备也是必不可少的. 未来光网络智能接收机有望在没有任何先验信息的情况下自主地监测网络中的各种调制格式信息.

调制格式监测技术已在无线通信[28]和认知无线电领域[30]研究多年. 近年来由于光通信网络更加趋近于灵活的自定义网络，这种监测技术引起了光通信领域研究人员的极大关注. 香港理工大学课题组[31]提出使用人工神经网络（artificial neural network, ANN）训练不同调制格式的异步振幅直方图以实现调制格式监测. 该方案需要额外添加调制格式监测模块，虽然能识别多种调制格式但在很大程度上增加了传输系统的复杂度，且神经网络算法的复杂度较高. 丹麦技术大学课题组[32]提出一种基于三维斯托克斯空间簇点识别的调制格式监测方案，该方案结合机器学习聚类算法获取三维斯托克斯空间簇点数目，实现了调制格式监测功能. 然而，随着调制格式阶数的增加，三维空间中的簇点数目也随之增加，以致在很大程度上增大了调制格式识别的复杂度和难度. 美国佐治亚理工大学课题组[33]提出了一种基于高阶统计矩的斯托克斯空间调制格式识别方案，但需要提前预知系统OSNR 信息且对高阶调制格式监测较为困难. 香港理工大学课题组[34]提出一种基于幅度直方图的深度神经网络方案，可实现多种调制格式的识别操作，但在识别过程中需要大量训练样本才能得到优化模型. 加拿大麦吉尔大学课题组[35]提出基于导频辅助的调制格式监测方案，但该方案需要额外的辅助编码，进一步增加了发射端的复杂度. 北京邮电大学课题组采用卷积神经网络（convolutional neural networks, CNN）监测星座图信息[36]，但需要在数字信号处理的末端实现监测，其实用性受到了很大的限制. 西南交通大学科研团队提出一种基于二维斯托克斯平面的调制格式监测方案，根据不同调制格式在二维平面中能级数的不同，实现多种常规调制格式的监测功能[37]；随后又提出了一种强度波形轮廓的调制格式监测方案，该方案通过判断不同调制格式的波形轮廓特征来实现调制格式监测功能[38]. 如表3 所示，本文首先总结了各种调制格式监测方案的技术特点，然后以基于强度波动的监测方案为调制格式参量监测案例详细分析了该方案的工作原理和实现结果.

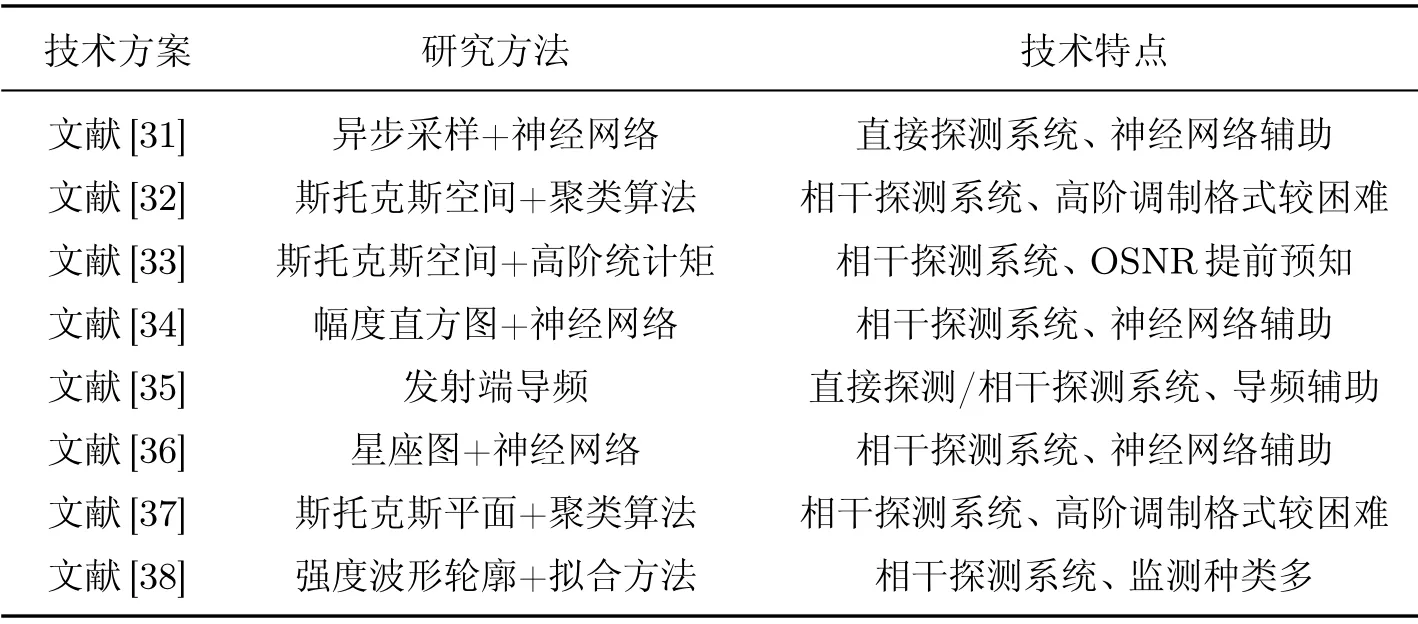
表3 调制格式监测技术方案总结Table 3 Summary for modulation format monitoring schemes

3.2 调制格式参量监测案例——基于强度波动的光调制格式监测技术

3.2.1 工作原理

经恒常模均衡算法补偿之后的数字信号D(n)可用来获取强度波动特征. 各种调制格式的强度波动特征如图8 所示，从图中可观察到不同调制格式呈现出不同的强度特征，主要是因为各种调制格式信号的强度能级不一样. 例如：QPSK 信号只有1 个幅度能级，16QAM 有3 个幅度能级，32QAM 有5 个幅度能级，64QAM 有9 个幅度能级，可见不同调制格式的强度波动特征也不相同. 因此，本文考虑以此特征作为区分不同调制格式信号的标准，其中强度波动的特征Godard’s 标准误差可定义为

式中，|D(n)|2表示接收到的数字信号D(n)的平方功率，R为信号的恒定功率值，E{|D(n)|4}为四次信号的平均功率，E{|D(n)|2}为二次信号的平均功率. 根据式(9)可知，Godard’s 标准误差代表着信号的强度信息与恒定功率值之差. 由于不同调制格式具有不同的强度能级，Godard’s 标准误差也会随之变化. 此外，将另一种强度波动特征（强度噪声方差）引入到本小节所提方案中，具体定义如式(5)所示. 由于不同调制格式将呈现不同方差，可以通过该特征来识别调制格式. 如图9 所示，本小节主要采样Godard’s 标准误差与强度噪声方差这两种强度波动特征所组成的二维平面图来区分各种调制格式信息. 二维波动特征平面图大致可分为3 个区间，分别为QPSK 调制格式区间、8QAM 调制格式区间以及混合的16QAM/32QAM/64QAM 调制格式区间. 通过支持向量机将3个区间分开，则QPSK 信号和8QAM 信号可从这个二维平面中区分开来. 因为16QAM、32QAM、64QAM 等高阶调制格式信号存在多个幅度级，所以直接通过二维强度波动特征图将很难区分. 正如图9 所示，高阶调制格式信号的强度特征在二维平面中混淆在一起，就不能直接使用支持向量机的方法在二维平面中进行区分，此时可用分集Godard’s 标准误差来进一步识别剩余的高阶调制格式信号.

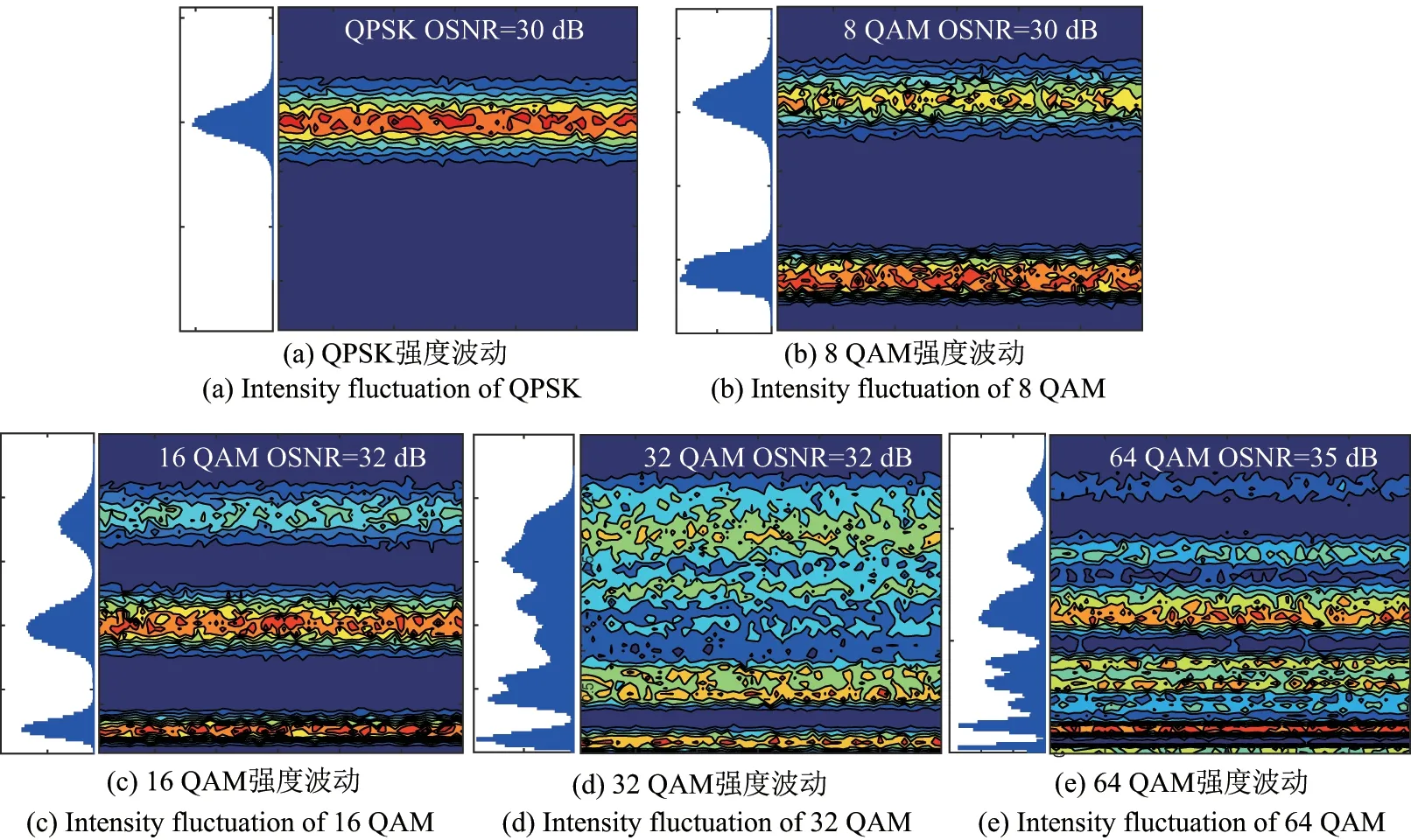
图8 5 种调制格式的强度信号波动Figure 8 Intensity signal fluctuation for five modulation formats

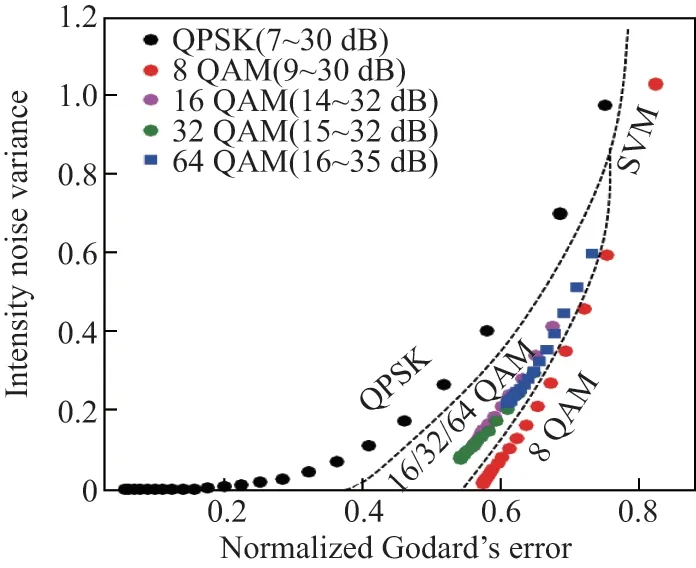
图9 不同调制格式的强度波动特征Figure 9 Intensity fluctuation features of different modulation formats

为了进一步区分16QAM、32QAM、64QAM 等高阶调制格式信号，本方案首先进行第1 步分集操作. 选择调制格式信号归一化强度的范围为0.7～1.4，计算Godard’s 标准误差.该范围是以16QAM 理想信号的中间幅度能级作为参考选取的. 在不同OSNR 条件下，第1 步分集操作得到的Godard’s 标准误差结果如图10(a)所示. 其中，16QAM 信号的OSNR 测试范围为14～32 dB，32QAM 信号的OSNR 测试范围为15～32 dB，64QAM 信号的OSNR 测试范围为16～35 dB. 从图10(a)中可获知，16QAM 调制格式信号的Godard’s 标准误差与其他两种调制格式的Godard’s 标准误差相比明显相差较大. 因此，可以找到一个优化的阈值Th1将16QAM 与其他两种调制格式区分开来. 然而，对于32QAM 信号与64QAM 信号，使用第1 步分集Godard’s 标准误差可能需要较高的OSNR 条件才能区分开来. 为了更好地区分剩余的高阶调制格式，该方案采用第2 步分集方法来辅助识别. 第2 步分集操作如图10(b)所示，该分集操作选择调制格式信号大于0.85 范围的归一化强度，计算Godard’s 标准误差. 该范围是以32QAM 理想信号第3 个能级以后的幅度作为参考选取的. 64QAM 在这个范围内呈现的幅度能级与32QAM 的幅度能级完全不一样，因此利用第2 步分集的方法是可以将两种信号完全分离开的. 其中，32QAM 信号的OSNR 测试范围为15～32 dB，64QAM 信号的OSNR 测试范围为16～35 dB. 可以发现利用第2 步分集操作计算得到的32QAM 信号与64QAM 信号的Godard’s 标准误差结果相差较大，因此可以从图中找到一个优化的阈值Th2将32QAM 与64QAM 区分开来.

图10 两次分集的Godard’s 标准误差图Figure 10 Normalized Godard’s criterion errors of twice partition operations

3.2.2 结果分析

为了验证本小节提出方案的监测性能，需要结合优化的训练样本数目和符号数目. 如图11 所示，本方案首先测试了背对背条件下的性能. 当PDM-QPSK/PDM-8QAM/PDM-16QAM/PDM-32QAM/PDM-64QAM 信号达到100%的正确识别率时，所需的最小OSNR 分别为7 dB、9 dB、16 dB、17 dB 和16 dB.图中的点线为不同种调制格式所对应的20%FEC（误码率为2.4×10−2）理论阈值. 由此可知，所有调制格式达到100%正确识别率时，所需的最小OSNR 比20%FEC 理论阈值更小，由此可见本小节方案具有很好的监测性能，有望给下一代光网络带来便利.

图11 5 种调制格式信号在不同OSNR 条件下的正确识别率Figure 11 Correct identification rates of five modulation formats under different OSNR values

为进一步验证该方案对非线性效应的容忍性，本文开展了一系列不同发射功率的长距离传输实验. 其中，PDM-QPSK 信号传输距离与发射功率范围分别设置为2 000 km 以及−4～10 dBm. PDM-8QAM 信号传输距离与发射功率范围分别设置为2 000 km 以及−3～6 dBm. PDM-16QAM 信号传输距离与发射功率范围分别设置为1 040 km 以及−3～8 dBm.PDM-32QAM 信号传输距离与发射功率范围分别设置为320 km以及−6～11 dBm. 文中采用误差向量幅度（error vector magnitude, EVM）来评价信号损伤的程度. 如图12 所示为不同调制格式在不同发射功率条件下的正确识别精度图. 当发射端功率大于2 dBm 时，由EVM性能可知所有调制格式都遭受到非线性损伤的影响. 反之，当发射端功率小于2 dBm 时，系统损伤主要来自于ASE 噪声. PDM-QPSK、PDM-8QAM、PDM-16QAM、PDM-32QAM 调制格式信号在实现100%正确识别率时所需要的最大发射功率分别为10 dBm、5 dBm、6 dBm、11 dBm. 值得注意的是，PDM-8QAM 和PDM-16QAM 信号所能承受的发射功率均小于PDM-QPSK 信号所能承受的发射功率. 这是因为在长距离传输以后，欧氏距离越小的星座图调制格式信号对链路中的噪声和损伤越敏感. 同时，PDM-32QAM 的最大发射功率为11 dBm 是因为传输距离相对较短. 由实验结果可知，该算法具有很强的非线性损伤容忍度.

4 讨论与总结

近年来，科研人员以单参量监测技术为研究基础开始探索少数参量联合监测，如2 个或3 个参量联合监测. 在直接探测的系统中，少数参量联合监测方面研究最为广泛的是异步采样时域监测技术，主要是通过对电信号幅度异步采样产生一维异步幅度直方图（asynchronous amplitude histogram, AHH）或二维异步延时抽头采样图实现信号性能监测的. 针对AHH 监测技术，文献[39]通过分析信号AHH 峰值高斯分布来实现色散与光信噪比双参量联合监测.随后，通过分析AHH 的幅度级变化特征实现色散与偏振模色散[40]、调制格式与符号率[41]双参量联合监测. 文献[42]通过结合神经网络的方法实现了色散、偏振模色散与光信噪比三参量联合监测. 针对二维异步延时抽头采样图监测技术，结合统计信号处理方法分别实现了色散与光信噪比[43]、调制格式与光信噪比[44]等双参量联合监测. 使用神经网络对二维异步延时抽头采样图进行精准分析，实现了调制格式、符号率与光信噪比[45]以及色散、偏振模色散与光信噪比[46]等三参量联合监测. 另外，基于相干检测方式的少数参量联合监测也引起了广泛关注. 对于色散与偏振模色散的双参量联合监测，主要采用时域均衡器抽头函数[47]、数据辅助[48]等方法. 对于调制格式与光信噪比双参量监测，主要研究方法是监测色散补偿以后信号的强度信息[49]和斯托克斯参量信息[50]，通过结合具有强大分类功能的神经网络技术实现双参量联合监测. 基于相干检测方式的三参量联合监测[51]还处于探索阶段，相关报道较少.

图12 4 种调制格式信号长距离传输之后的正确识别率Figure 12 Correct identification rates of four modulation formats under long-distance transmission links

当前，光纤通信系统性能监测方面的研究工作主要集中在单参量监测和少数参量联合监测方面. 未来精细化、一体化的多参量联合监测将成为安全可靠光纤传送网必不可少的研究方向. 此外，利用深度学习技术实现光纤传输系统结构监测，可为性能监测方面的研究提供全新的思路. 通过前期对关键参量的训练分析，深度学习技术可更加方便地辅助光纤传输系统，实现链路损伤参量的精准分离以及多参量精细化联合监测；可大大降低系统的成本与复杂度，并有效提升性能监测与故障诊断的智能化水平. 未来利用多参量联合监测模块获取多个链路损伤参量，可为评价网络传输链路物理状态提供参考，使网络由传统的被动处理转为主动预防，这对提升网络智能化管理水平和预测能力具有重要的应用价值.