融合煤矿多维时序数据的瓦斯异常检测算法

丁 汀，颜登程，张以文，周 珊

(1.安徽大学 计算机科学与技术学院，安徽 合肥 230601；2.安徽大学 物质科学与信息技术研究院，安徽 合肥 230601；3.深圳易伙科技有限责任公司，广东 深圳 518000)

0 引言

煤炭是我国的重要矿产能源之一，对国民经济的发展具有非常关键的作用，但是矿井下自然环境恶劣，情况复杂，导致我国煤矿灾害事故时有发生，不仅给煤矿企业带来了经济损失，还给矿井工作人员的生命安全造成了致命的威胁。在诸多事故起因中，瓦斯事故是煤矿安全的头号杀手。为了预防瓦斯灾害，矿井通过安装煤矿安全监测系统采集井下实时环境数据，分析、挖掘矿井瓦斯实时环境数据中的安全信息和异常状态，对预防瓦斯灾害具有重大意义。当前的煤矿安全监测系统可以帮助煤矿工作人员了解矿井下的情况，在一定程度上保证了安全生产，但是监测系统在煤矿生产过程中产生的海量数据未得到充分挖掘和利用，数据信息独立保存，对数据的规律研究较少，大量数据的价值未得以体现。

异常检测是指识别特定应用领域中的异常模式，并通过分析异常模式的特性来提供决策支持、保障安全等[1]。异常检测的研究正广泛应用于各个领域，其中就包括煤矿领域。矿井瓦斯异常检测系统是煤矿安全生产业务流程的重要手段，由于矿井下地质条件复杂、设备众多、环境恶劣、瓦斯传感器探头失效和不按规定放置等因素，仅靠煤矿安全监控系统的瓦斯传感器测量到超限报警，结果并不准确，安全监控系统中的大量多维时序数据没有得到有效应用。针对这种情况，本文利用智慧矿山所产生的大数据进行多维、多方位的挖掘分析，采用多参数分析对瓦斯浓度、一氧化碳浓度、风速等数据进行综合处理和优化，找出数据的内在联系和规律，提出一种融合煤矿多维时序数据的煤矿瓦斯异常检测算法(Gas Anomaly Detection algorithm Merged with Coal Multi-dimensional time series Data, GADMCMD)，有效提高了煤矿事故风险防控能力。

本文的主要贡献如下：

(1)融合多种类传感器时间序列数据，基于局部敏感哈希在高维数据处理上的优势，以及孤立森林优异的异常检测效果，提出一种适用于煤矿多维数据场景的瓦斯异常检测算法。

(2)通过在每个滑动窗口建立相应的局部敏感哈希孤立森林，并根据每个滑动窗口内的异常率自动更新异常检测模型，使得本文模型对不同的异常模式均具有很高的检测精度。

(3)使用真实的煤矿安全监测数据集对所提出的方法进行了实验评估，结果表明，本文所提出的方法能够很好地处理真实场景下煤矿瓦斯浓度异常检测问题。

1 相关工作

目前，已经有很多异常检测的方法，大致可分为基于统计的方法[2]、基于邻域的方法[3]、基于分类的方法[4]、基于隔离的方法[5]。这些方法在特定领域都有其优势，但是，在流数据中，这些方法都有一些缺点而不能直接运用于流数据异常检测。

基于统计的方法通常利用统计学方法建立一个模型，随后考虑对象有多大概率可能符合该模型，即考察不和谐的观测值[6]。与假定模型或分布规律不相符合的数据有较大的概率为异常值。此类方法的优点在于拥有丰富、成熟的统计知识作为理论支撑，对于检测出的异常点，有良好的可解释性。但它高度依赖于数据模型分布的假定，即要求有大量的先验知识，而在真实应用场景下，数据集很难服从该假定[7]。其次，该方法对于单个属性的异常点检测效果较好，对于高维数据，可能会因为没有合适的模型和分布而导致检测性能很差。

基于邻域的异常点检测方法主要通过比较每个数据对象与其邻域中邻居的距离来判断异常。此类方法使用常用的距离概念来计算两个数据对象之间的距离，若数据对象远离其邻居，则可认为该数据对象为异常值。最具代表性的就是局部异常因子(Local Outlier Factor, LOF)算法[3]，该算法通过计算数据对象的k个最近邻的平均局部密度与数据对象自身的局部之比来判断异常。由于LOF算法对参数k较为敏感，k值选取不当往往会导致检测性能下降，为此，Pokrajac等[8]提出了基于连接性的异常因子算法(Connectivity based Outlier Factor, COF)。该算法根据给定参数最少邻居数k,首先计算数据对象与其k近邻间的平均连接距离，若数据对象的平均连接距离大于它的k最近邻的平均连接距离，则该数据对象为异常值。由于COF算法计算量较大，在处理大规模数据集时会出现效率较低的问题。基于局部距离的异常因子算法(Local Distance-based Outlier Factor, LDOF)[9]首先计算数据对象到k个近邻距离的均值，然后计算k个近邻彼此之间的距离均值，最后以二者的比值作为衡量异常的标准，但该算法因为运行速度较慢而不适用于大规模高维数据集，且依赖参数k，若k值选取不当则会影响检测精度。

基于分类的异常点检测方法主要利用有标签的数据对象训练出分类器，然后该分类器将待检测数据对象划分到异常或者正常类别。由于数据标签种类不同，分类形式多样，基于分类的异常检测方法分为单分类的异常点检测和多分类的异常点检测。单分类的异常点检测的关键在于建立一个清晰的决策边界。典型的算法如一类支持向量机算法(One Class Support Vector Machine, One-Class-SVM)[10]，该算法在特征空间中获得数据周边的球形边界，判定边界内的数据为正常，边界外的数据为异常点。但该方法要求已知的应用场景下的数据集边界清晰且正常点较多，同时效率较低。Rajasegarar等[11]提出一种基于SVM的技术，用于传感器数据中的离群值检测。该方法使用一类四分之一球体来减少SVM计算复杂度的工作量并局部识别每个节点处的异常值。位于四分之一球体之外的传感器数据被视为异常值。多分类的异常检测方法是从数据集学习出多个边界，将不属于任何边界内的数据点划分为异常点。典型的方法有基于神经网络的多分类异常点检测[12]与贝叶斯网络[13]，基于神经网络或贝叶斯的异常检测方法分为两个阶段：第一个阶段通过给定的正常的、有标签的多分类数据来训练模型[14]；第二个阶段将待检测数据输入模型，若网络接收则为正常点，反之为异常点[14]。

针对上述问题，本文提出一种融合了多维煤矿时序数据与局部敏感哈希孤立森林的瓦斯浓度异常检测算法，该方法将滑动窗口与局部敏感哈希孤立森林相结合，不仅能够降低高维环境下的时间开销，还能解决因瓦斯探头失效、不按规定放置而引起的误报、漏报等问题，可有效提高瓦斯异常检测精度。

2 背景知识

2.1 局部敏感哈希

局部敏感哈希(Locality Sensitive Hashing, LSH)[15]是一种从海量的高维数据集合中找到与某个数据最相似的一个或者多个数据的高效方法。其基本思想是：在高维数据空间中的两个相近数据被映射到低维数据空间中后，将有很大的概率保持相近；原本不相近的两个数据，在低维空间中也将有很大的概率不相近。局部敏感哈希定义如下：

对于原始数据空间中的任意两个点x和y，d(x,y)表示x和y的距离，f(x)表示x的哈希值，若对哈希函数族F中的任意一个哈希函数f∈F，同时满足条件式(1)和式(2)，则称该哈希函数族F为(d1,d2,p1,p2)-sensitive。

d(x,y)≤d1⟹P(f(x)=f(y))≥p1，

(1)

d(x,y)≥d2⟹P(f(x)=f(y))≤p2。

(2)

事件f(x)=f(y)表示x和y会被映射到同一个桶中，为了保证局部敏感哈希函数有效，需满足p1≥p2。从哈希函数族中随机选取多个(α)哈希函数，生成连接的组合哈希值，并根据这些哈希值决定两个数据实例是否被哈希到较为相近的数据空间中。这种策略能减少负样本被模型预测为正样本的事件，即误报率(false positive)降低，从而提高了相似搜索的精度。同时，建立多个(β)哈希表减少了正样本被模型预测为负样本的事件，即漏报率(false negative)。LSH的另一个显著特征是其进行相似计算时的线性时间复杂度，而传统的往往是平方级复杂度。因此，LSH已被广泛运用于各种领域，如数据库中的快速近似最近邻搜索和数据挖掘[16]。

由于相似搜索质量受α影响，需要调整参数以求获得良好的性能。其后，一种名为LSH forest的数据结构通过使用可变长度的组合密钥来减轻参数调整的任务量[17]。其核心思想是每个数据实例的组合密钥足够长，以确保每个实例具有不同的密钥。具体地，在所有组合密钥的集合上构造被称为LSH树的(逻辑)前缀树，其中每个叶节点对应于数据实例，使用不同的LSH函数对各个节点产生路径标签并进行分割。从根到叶节点的路径标签组成对应数据实例的组合键。

2.2 孤立森林

孤立森林(isolation Forest, iForest)是一种基于集成学习的异常检测方法，该方法检测精度高、时间复杂度低[5]。iForest适用于连续数据的异常检测，将异常定义为“容易被孤立的离群点”，即分布稀疏且离密度高的群体较远的点。在数据空间里面，分布稀疏的区域表示数据发生在此区域的概率很低，因此可认为落在这些区域里的数据是异常的。

iForest属于无参数、无监督式方法，无需定义数学模型也不需要标记，iForest由若干个iTree构成。iTree学习过程随机，随机抽取特征、随机选取分割值来建立决策树，从而将每一个样本分到一个独立的子节点上。iForest具有线性时间复杂度，由于采用了基于集成的方法，每个iTree之间相互独立，可以用在海量数据的数据集上面。算法的稳定性通常随着树的数量增大而提高。但iForest随机选取特征、维度的特性也使得该算法存在缺陷，不适用于特别高维的数据，由于在高维度的数据空间中，即使iForest构建完成后，也会有冗余的维度信息存在，导致算法可靠性降低，还可能因为大量噪音维度或无关维度而影响树的构建[18]。

3 GADMCMD检测方法

从孤立的角度来看，局部敏感哈希孤立树(LSH tree)本质上也可以视为孤立树，因为每个数据实例都与其余数据实例是分隔开来的。因此，局部敏感哈希孤立森林(LSH iForest, LSHiForest)可以用于基于集成方法的孤立机制的异常分析。异常检测包含两个阶段，如图1所示：训练阶段从每个滑动窗口中以不放回采样的方法建立局部敏感哈希森林；评估阶段利用已建立的局部敏感哈希森林，计算数据实例的异常得分及异常率，若异常率高于给定阈值，则在下个滑动窗口更新已建立的检测模型。

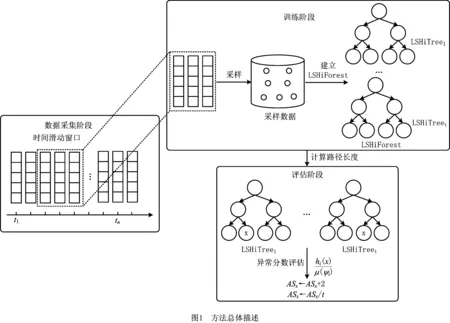
3.1 采样

在训练阶段，通过给定局部敏感哈希函数族，递归使用哈希函数族，建立LSH tree，直到数据空间中的所有数据实例被分隔。使用多种不同的采样方法挑选出输入数据的数据空间[19]，数据采样率遵循均匀分布U(min{1,50/n},max{1,1 000/n})，其中n为数据集中数据实例的个数，如果采用该采样方法生成的LSH tree树高不能遵循均匀分布。Ψ控制着训练数据的大小，当Ψ增长到某个特定数值时，LSHiForest达到较高的可靠性，如果Ψ继续增加，在检测精度上不会获得增长，只会增加处理时间和内存开销。在实际情况中，异常通常是少数且不同，正常点是多数且很类似[5]。因此，较小的采样大小足以使LSHiForest区分异常和正常[20]。

本文的采样率为min{1,2s/n}，s遵循均匀分布U(6,10)。特别是如果n≥64，Ψ的变量范围为[64,1 024]。

3.2 构建局部敏感哈希森林

在获得数据样本后，需要计算LSH tree的树高H(Ψ)。如果两个数据实例十分接近，会导致LSH tree增长得非常大，因为LSH函数为两个相同的数据实例生成了相同的哈希值，通常需要更多的哈希函数产生更多的哈希值，以便区分这些非常接近的实例，但这样会生成长单分支路径。从计算成本的角度看，限制LSH tree的高度是必要的。高度限制对于异常检测的效果几乎没有影响，具有更大深度的数据实例通常是正常值而非异常。此外，压缩单分支路径，使得具有这种长路径的异常示例也可以被检测算法识别。但LSH tree必须足够高，以确保数据能被充分隔离。构建LSHiForest的过程如算法1所示。

算法1构建LSHiForest。

输入:数据集X;局部敏感哈希函数簇F;局部敏感哈希孤立树个数t;滑动窗口集Z;

输出:局部敏感哈希孤立树集合{Ti|1≤i≤t}。

Begin

1:for j,1≤j≤n do:

2: for i,1≤i≤t do:

3: Si←variable_subsampling(X);

4: Compute a height limit:Hi(Ψ);

5: Ti←LSHiTree(Si,F,Hi,0);

6: return{Ti}。

7: return{Zj}。

End

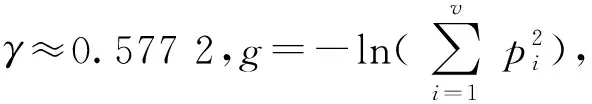
2log2(ψ)+0.832 7。

(3)

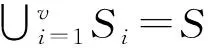
算法2构建局部敏感哈希孤立树:LSHiTree(S,F,H,I)。

输入:输入数据S;哈希函数族F;树高限制H;索引I;

输出:一棵局部敏感哈希孤立树T。

Begin

1: if |S|=0 then

2: return NULL;

3: else if |S|=1 OR I>H then

4: return node{Size←|S|Hash_Index←I,Children←∅};

5: else

6: {K1:S1,…,Kv:Sv}←lsh_split(S,fI),fI∈F;

7: While v=1 AND I≤H do:

8: I←I+1;

9: {K1:S1,…,Kv:Sv}←lsh_split(S,fI);

10: if I>H then

11: return node{Size←|S|,Hash_Index←I};

12: Initialise child node indexing:T←∅;

13: for i,1≤i≤v do:

14: Ci←LSHiTree(S,F,H,I+1);

15: T←T∪{Ki:Ci};

16: return node{Size←|S|,Hash_Index←I,Children←C}。

End

3.3 异常评估

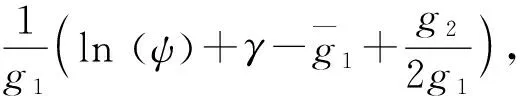
(4)

由于v的信息未知，需要从训练完成的LSH trees中评估它。具体来说，从平均分支因子来评估v。

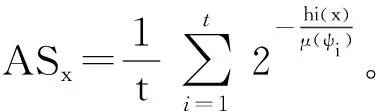
算法3预测异常分数。

输入 测试数据X;LSH函数簇F;LSH forest {Ti|1≤i≤t};路径调节因子η;粒度级别L;异常率ε;异常率阈值u；

输出 Anomaly scores {ASx|x∈X}。

Begin

1:if ε

2: Constructing LSHiForest();

3:else:

4: for x∈X do:

5: ASx←0;

6: for i,1≤i≤t do:

7: hi(x)←path_length(x,F,Ti.root,η,L,0);

9: ASx←ASx/t;

10: return {ASx}。

End

算法4详细介绍了path_length(x,F,node,η,L,Icur)子程序，计算实例x从根节点到相应叶节点的路径长度。当Icur=0时，可以得到关于整棵树的h(x)，深度级别为L,1≤L≤H，是用户定义的用于限制遍历深度的参数，与iForest中的高度限制相同。此外，本文还使用μ(node.Size)来调整路径长度，因为叶节点或者深度等于L的内部节点可能对应有多个数据实例，通常来说，同一深度下较大子树中的数据实例比小子树中的更加正常。

算法4路径长度path_length(x,F,node,η,L,cur)。

输入 数据实例x;局部敏感哈希函数族F;当前节点node;调节因子η;粒度级别L;索引I；

输出x到根节点的路径长度。

Begin

1:if node=NULL then

2: return-1;

3:else if node.Children=∅ OR Icur>L then

5:else

6: K←fHash_Index(x),fHash_Index∈F;

7: if ∃(Ki:Ci)∈node.Children AND K=Kithen

8: return path_length(x,F,Ci,h,L,Icur+1);

9: else

End

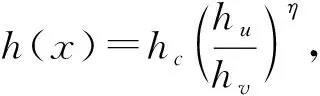
3.4 时间复杂度分析

关于样本大小，LSHiForest的计算复杂度类似于iForest，具体来说，训练阶段的平均情况时间复杂度为O(ψlogv(ψ))，评估阶段的平均情况时间复杂度是O(logv(ψ))。由于大多数LSH函数具有O(1)时间复杂度，因此本文方法可以非常快。

4 实验分析

4.1 数据集

为验证基于LSHforest的煤矿瓦斯异常检测模型的可行性，以及本文算法GADMCMD的有效性，使用真实数据集进行测试，该数据集是由淮南煤矿集团朱集东矿提供的矿山监测数据，时间区间为2017年3月10日～2017年9月9日，所有传感器每间隔10 s收集一次数据。监测值包括同一工作面下的瓦斯浓度、风速、一氧化碳浓度、二氧化碳浓度、氧气浓度、温度、日产量、煤尘浓度。

实验环境为：编程语言为Python，实验机器配置为16 G内存，Core i7-49703处理器，Windows操作系统。

4.2 评估指标

为评估本文方法的检测性能，采用AUC(area under curve)[22]作为评测指标，AUC是一个二分类模型评价指标，是ROC(receiver operating characteristic)曲线下面区域的面积，以量化ROC曲线性能。ROC曲线基于样本的真实类别和预测概率，其纵轴为真正率(TPR)，横轴为假正率(FPR)：

(5)

(6)

AUC的值越大，说明分类模型的性能越好，对于最理想的分类模型，其AUC值等于1；对于随机分类模型，其AUC值为0.5。

4.3 性能对比

为更好地评估本文方法GADMCMD的性能，选择以下几种较经典的方法在AUC指标上进行对比实验。

(1)基于移动窗口方案的方法[7](BFMW)。一种基于统计的异常检测方法，通过滑动窗口，改进了k-σ检验方法，超出区间的为异常。

(2)基于孤立森林的时序异常检测方法[23](iForestASD)。基于孤立森林与滑动窗口的异常检测算法，通过递归地随机分割数据集，直到所有样本点都是孤立的，通过路径长短判断待检测点是否为异常点。

表1为本文方法及对比方法的重要参数。

表1 算法重要参数

表2是采用0.1%～3%的异常样本比例在不同方法的检测效果。观察本文提出算法下的3种局部敏感哈希函数——ALSH、L1SH、L2SH，与其他异常检测方法相比，在各种异常发生率的场景下均具有更大的AUC，即更佳的检测精度，特别是L1SH、L2SH与其他方法相比，在多数情况下都有更出色的检测效果，这表明本文方法具有更优的检测效果。iForestASD和LSHiForest框架下的ALSH、L1SH、L2SH在真实的煤矿瓦斯数据集下都有相对稳定的性能，并能够避免最坏情况的出现，这是因为此类方法与数据分布无关。在现实情况中，如果出现瓦斯传感器损坏，瓦斯监测系统会维持某个恒定值，导致漏报，此刻的AUC值为0，而本文方法能够综合利用与瓦斯具有关联关系的数据，如一氧化碳浓度、风量，与传统办法相比，漏报率显著降低。因为综合使用了多维数据，可以发现本文算法在高维数据情形下表现很好，这是因为LSH最初的提出是为了解决高维数据下的最近邻搜索问题。总体而言，本文算法在高维数据空间、不同异常比例条件下，都具有优异的异常检测效果，特别是L2SH，同时拥有高检测精度和鲁棒性。

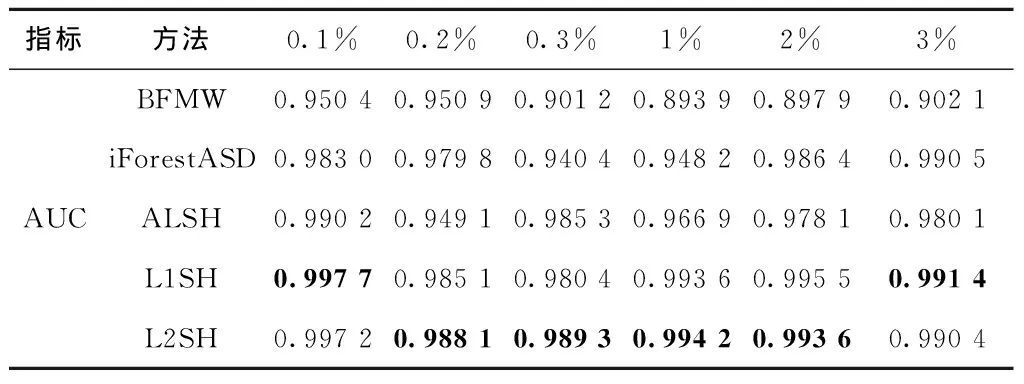
表2 检测性能对比

4.4 LSH tree个数对检测精度的影响

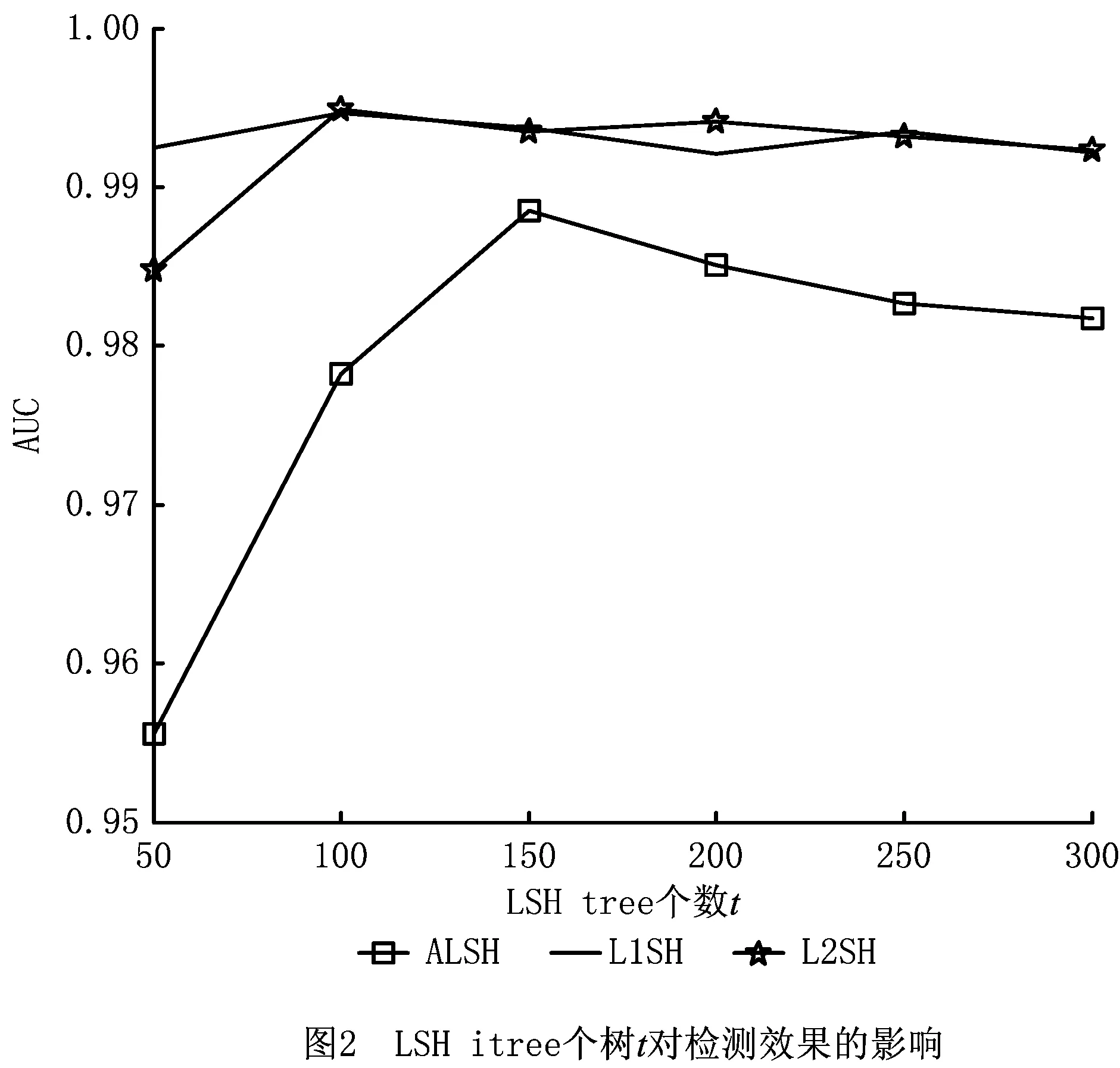
本节均采用1%的异常比例来评估LSH tree的个数t对本文算法检测精度的影响。t决定了LSHiForest中森林的大小，t越大，森林越大，设置异常样本比例为1%，T=3 600，t值分别为50，100，150，200，250，300。如图2所示，本文算法下的3种函数下AUC的值随着t值的增加而增加，但是当t超过某个阈值时，AUC的值随之下降。这说明t取适当的值有利于提高检测精度。因为当t取值过小时，LSH tree的个数较小，数据的实际利用价值低，从而降低了检测精度；而当t=100时，每个数据的路径长度已经覆盖较好，检测效果最佳，且L2SH方法具有最高的检测精度。

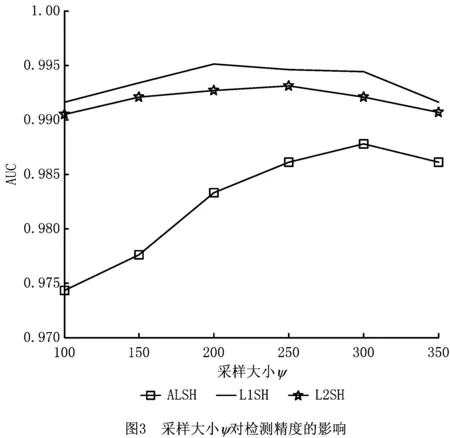
4.5 采样大小ψ对检测精度的影响

为评估采样大小ψ对本文算法检测精度的影响，参数ψ决定建立每棵LSH tree所需样本的大小，本文设置异常样本比例为1%，t=100，T=3 600并将采样大小从100变化到350，步长设为50。从图3可以看出，3种方法在开始时，随着采样大小的增加，AUC的值也随之增加，当采样大小超过某个数值时，AUC的值会下降。这说明，适当大小的采样有利于提高检测精度。采样是为更好地将正常数据和异常数据分离开来，采样数据越多，检测效果越好，对于本文方法而言，如果采样过大，建立LSH tree后仍然有大量的信息没有被使用，导致算法的可靠性降低，还会存在大量噪音数据，从而影响LSH tree的构建。图3显示，对于不同方法，在ψ选取相应的取值时，AUC能达到其最大值，检测效果最佳。

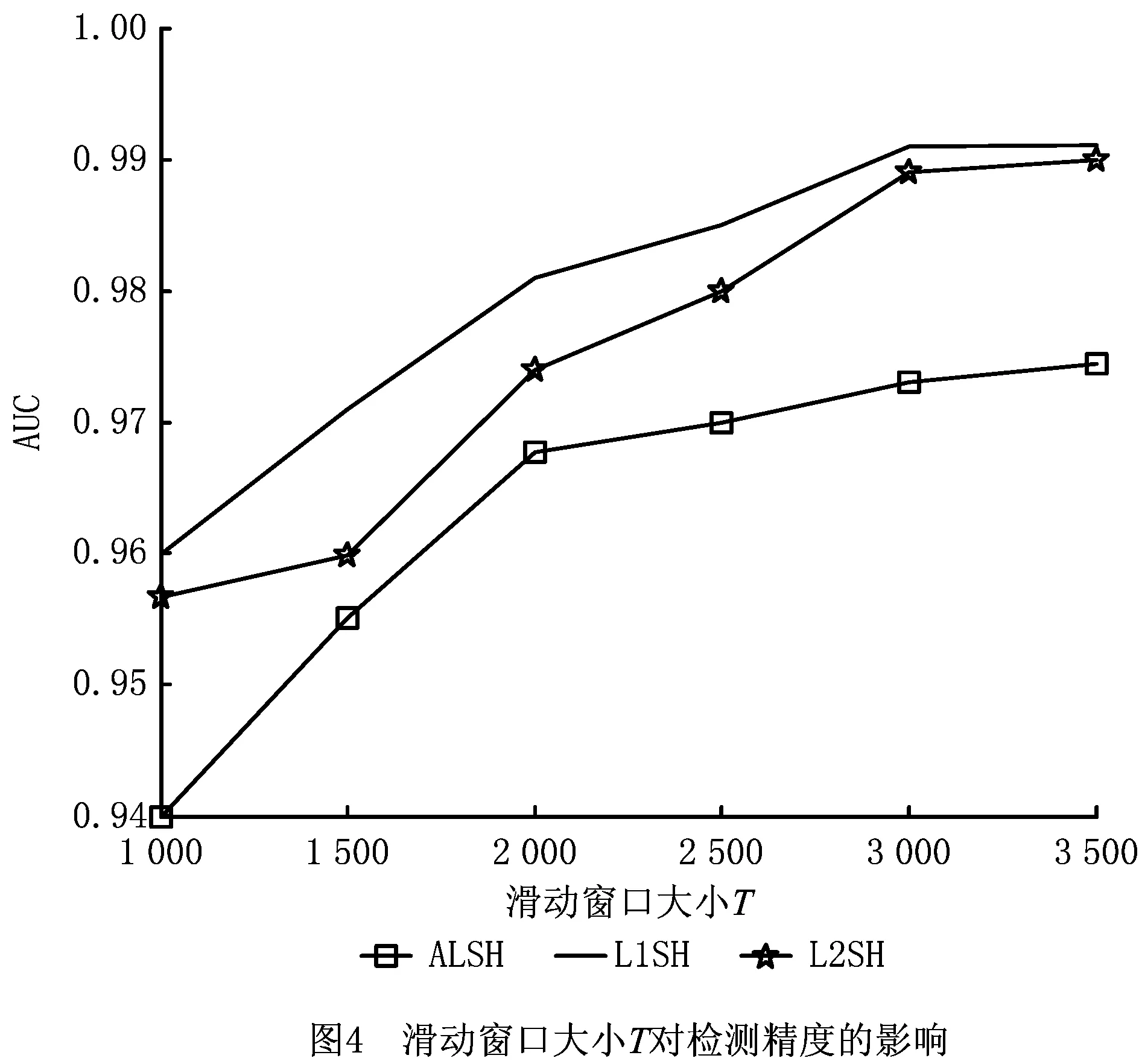
4.6 滑动窗口大小T对检测精度的影响

为评估滑动窗口大小T对本文算法检测精度的影响，设置异常样本比例为1%，t=100，并将滑动窗口大小从1 000变化到3 500，步长设置为500，从图4可以看出，3种方法在开始时，AUC的值都会随着滑动窗口大小的增加而增加，当窗口大小超过某个数值时，AUC的值接近稳定，保持不变。这说明，增大滑动窗口的大小有利于提高检测精度。因为滑动窗口内的数值越多，可采样的信息越充分，当超过临界值后，过多的信息没有被使用，无法再提高检测精度。

5 结束语

本文提出一种融合煤矿多维时序数据的煤矿瓦斯异常检测算法。该方法在每个窗口对包括瓦斯浓度在内的多维数据采样后，利用LSH建立LSHiForest，随后针对每个待检测样本，遍历森林中的每一棵树，通过其平均路径长度来计算异常得分。本文在真实的淮南朱集东煤矿数据集上进行了大量实验，结果表明，本文方法的瓦斯浓度异常检测精度与以往方法相比有显著提高，不仅解决了瓦斯浓度异常检测问题，还解决了因瓦斯探头失效而造成的异常漏报或误报问题。

本文提出的方法虽然具有较低的时间复杂度，但依然存在一些需要改进的地方，在实际工程应用中，越快检测出异常，意味着煤矿安全调度人员就有更多的反应时间采取相应的应急措施，后期研究可以考虑进一步优化算法，降低时间开销。