基于数据生成—消耗依赖的语义工作流并行化重构方法

孙晋永,闻立杰,匡增雄,李 涛,张 展

(1.桂林电子科技大学 广西可信软件重点实验室,广西 桂林 541004；2.清华大学 软件学院，北京 100084)

0 引言

业务过程的质量和运行效率是现代企业和组织在竞争中保持优势的关键因素。业务过程管理(Business Process Management, BPM)研究关注企业和组织的业务过程管理、分析、控制与改进，以提高业务处理效率，改进产品质量和提高服务水平[1]。而BPM技术可以被用于快速构建和更新过程感知信息系统，是现代企业和组织信息系统的共性基础性技术[1]。业务过程的改进与优化主要通过业务过程模型研究业务过程的改进、重构和优化问题，以提高业务过程的运行效率。

语义工作流[2]是一种基于领域知识的工作流，为业务工作流管理(Business Workflow Management，BWM)提供了丰富的语义和数据或资源信息。它同时包含控制流和数据流[2]，适于建模以控制流为中心，兼顾数据流的业务过程。与传统工作流相比，语义工作流更适合建模工业环境中的生产制造过程，可以为工业大数据系统软件的开发及运行提供一定的基础支持[3]。目前，语义工作流的应用已经涵盖了业务过程、电子商务、医疗、软件开发、科学分析和工业生产制造等领域[4]。

如果语义工作流中的任务能够尽可能地并行执行，则同等条件下运行效率就更高。因而重构语义工作流，提高它的并行任务数量是提高运行效率的方法之一。在软件工程领域，已有关于代码并行化重构的研究，目标是提高代码在多核处理器上的执行效率[5-8]。但现有的代码并行化重构方法并不能解决业务过程的并行化重构问题。Vanhatalo等[9]提出一种基于细化过程结构树的业务过程模型重构技术，完善一个业务过程模型使之结构性更好。Weber等[10]总结了一组业务过程模型库重构技术来简化过程模型库，使得模型管理人员能够高效地处理复杂的业务过程模型，更方便地维护业务过程模型库。Dijkman等[11]提出一种能自动探测业务过程模型的4种类型重构机会的技术。Leopold等[12]提出一种重构业务过程模型中活动标签的方法，以提高活动标签的质量。Polyvyanyy等[13]提出一种对无环业务过程模型进行结构化的方法。以上方法可以保持业务过程模型的行为，使过程模型更易理解和维护，但并不能处理业务过程模型的并行化重构问题。Jin等[14]首次提出一种基于带数据的工作流网(Workflow net with data, DWF-net)的业务过程模型并行化重构算法。算法先获取DWF-net对应的标签Petri网的任务执行(顺序、并行或互斥)关系，然后分析任务(变迁)节点上的数据读—写依赖，得出基于数据操作依赖的任务并行关系，最后使用α算法[15]构造并行化的DWF-net。重构后的DWF-net改善了业务过程模型的质量，提升了业务过程处理的效率。

针对提高基于语义工作流的业务过程运行效率的需求，本文在文献[14]的基础上，研究了语义工作流的并行化重构方法，提出基于数据生成—消耗依赖的语义工作流并行化重构方法。本文主要贡献如下：

(1)提出了基于数据生成—消耗依赖的任务因果关系、传递任务因果关系和关键任务因果关系的概念及获取方法。

(2)提出了基于数据生成—消耗依赖的任务执行关系更新规则，并据此设计了基于数据生成—消耗依赖和兼顾资源约束的交互式语义工作流并行化重构算法。

(3)提出一种语义工作流的并行度计算方法以评估并行化后的语义工作流的并行程度。

(4)实现了一个交互式的语义工作流并行化重构软件。

(5)通过仿真实验得出，本文的语义工作流并行化重构算法提高了语义工作流的并行度，改善了语义工作流的质量，为提高基于语义工作流的业务过程运行效率提供了基础条件。

1 预备知识

语义工作流最初由Bergmann等[2]提出。为传统工作流的任务节点描述增加语义并加上输入和输出数据对象，为边增加语义，使得工作流同时包含控制流、数据流和语义约束，得到了语义工作流[16]。与传统工作流相比，语义工作流不仅描述了业务过程中任务之间的控制流关系，还描述了任务的语义、数据或资源以及任务连接的语义等重要信息。

语义工作流可以被形式化为语义标注有向图[2]，定义如下。

定义1语义工作流[2]。语义工作流可以形式化为语义标注有向图W=(N,E,S,τ)。其中：N=NT∪NC∪ND，NT为任务节点的集合，NC为控制流节点的集合，ND为数据节点的集合；E⊆N×N为边的集合；S:N∪EΣ将节点或边映射为语义描述，Σ是一个领域相关的语义元数据语言；τ:N∪Etype将每个节点或边映射为一个类型。

为简化分析，本文仅研究块结构化的语义工作流，探讨它们的并行化重构方法。

例1图1为描述意大利面食(Pasta with fennel tomato sauce)制作过程的语义工作流SW1。

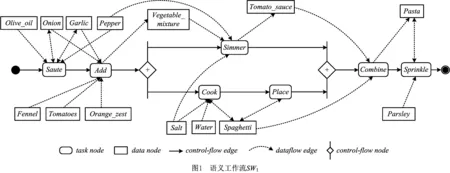
在定义1中，任务节点task∈NT执行的操作可以解释为：task以其语义描述taskDescp∈Σ指示的方式消耗其输入数据集合dataIn中的数据对象，生成其输出数据集合dataOut中的数据对象。在图1中，若将语义描述为“Saute”的第一个任务节点记为t1，则t1执行的操作可解释如下：t1以其语义描述“Saute”指示的方式消耗了集合S1={Olive_oil,Onion,Garlic,Pepper}中的数据对象，生成输出数据对象集合S2={Onion,Garlic}。

借鉴文献[15]中基于日志的序关系(log-based ordering relation)概念，本文定义语义工作流基于日志的任务执行关系。

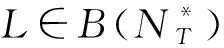
(1)a>Lb：当且仅当存在SW的一个执行轨迹tr=t1,t2,t3,…,ti,ti+1,…,tn(i∈{1,2,…,n-1})满足tr∈L，ti=a且ti+1=b。

(2)a→Lb：当且仅当(a>Lb)∧¬(b>La)成立；a←Lb：当且仅当(b>La)∧¬(a>Lb)成立。

(3)a||Lb：当且仅当(a>Lb)∧(b>La)成立。

(4)a#Lb：当且仅当¬(a>Lb)∨¬(b>La)成立。

对于定义2中的a→Lb，称a,b存在因果关系。←L是→L的逆关系，关系→L可以传递。

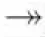
为了分析任务节点间的数据生成—消耗依赖，本文定义如下3个基于数据生成—消耗依赖的任务因果关系。

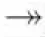
定义5基于数据生成—消耗依赖的传递任务因果关系。在语义工作流SW中，对于任务节点t1,t2,t3∈NT，如果存在数据对象x,yND，使得成立，则称t1,t3存在基于数据生成—消耗依赖的传递任务因果关系，记为关系可以进一步传递。

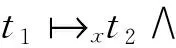
2 语义工作流的并行化重构算法

研究者一般使用与业务流程建模与标注(Business Process Modeling Notation, BPMN)语言类似的工具来描述语义工作流[2]。通过分析发现，如果语义工作流的一些任务间不存在数据生成—消耗依赖，则没有必要顺序执行，可以并行执行。于是识别出这些可并行的任务，据此对语义工作流进行并行化重构，可以得到并发程度更高的语义工作流。并行化后的语义工作流质量更好，可以为提高业务过程的处理效率提供基础支持。

2.1 化简语义工作流

在语义工作流的互斥结构块中每次只有一个互斥分支能被执行，而循环结构块中的任务节点需要被执行多次，因此在对语义工作流进行并行化重构时，不能将互斥结构块和循环结构块内部的任务节点与它们外部的任务节点等同看待。同时，由于互斥结构块、循环结构块的自身特点，它们内部也不能完全达到并行化，仅可以对它们内部的顺序执行分支进行一定的并行化操作。因此，有必要在并行化重构前对语义工作流进行适当化简。

本文采用如下方法化简语义工作流：识别出语义工作流的最外层互斥结构块和循环结构块，将这些结构块替换为特殊的“块节点”。这些“块节点”的输入数据是对应结构块的输入数据对象，输出数据是对应结构块的输出数据对象，这样可以得到化简的语义工作流。

于是，原语义工作流的并行化就转换为对化简的语义工作流的并行化。在对化简的工作流进行并行化重构时，将“块节点”与其他任务节点等同看待。化简算法的伪代码如算法1所示。

算法1语义工作流化简算法getReducedSWF。

输入：语义工作流SW1;

输出：简化的语义工作流SW2。

1 SC1=EC,1,SD1=ED,1

2 bList=getSWFBlocks(SW1) //获取SW1的互斥结构块和循环结构块列表

3 for each block in bList do

4 get block’s old control-flow edges set S1, new block-task node edges set S2

5 get block’s old dataflow edges set S3, new block-data object node edges set S4

6 SC1=SC1-S1+S2,SD1=SD1-S3+S4

7 EC,2=SC1,ED,2=SD1

8 SW2=(N1,EC,2∪ED,2,S,τ)

9 return SW2;

算法1中第1行的EC,1，ED,1分别是SW1的控制流边集合、数据流边集合，第7行的EC,2，ED,2分别是SW2的控制流边集合、数据流边集合，第8行的N1是SW1的节点集合。设SW1中互斥结构块和循环结构的总数为m，可得算法1的时间复杂度为O(m)。若语义工作流本身为一个互斥结构块或循环结构块，则将该结构块的每个分支作为一个语义工作流片段，先使用算法1进行化简，再对每个分支进行并行化。

2.2 获取语义工作流的任务执行关系

借鉴标签Petri网表示的过程模型的任务执行关系矩阵[14]获取方法，本文对其进行改造，使之适用于语义工作流，获取语义工作流基于日志的任务执行关系矩阵。首先，对语义工作流的任务节点和控制流节点按层进行编号；然后，基于节点的编号计算两个任务节点的最近公共前驱[14]，据此判断任务节点间的因果/并行关系；最后，得到任务执行关系矩阵。其中存在因果关系的任务节点对是本文的研究重点。

对节点按层编号以及计算最近公共前驱的算法是参考文献[14]中的相应算法，稍作改造得到。此处省略它们的伪代码。计算任务执行关系的伪代码如算法2所示。

算法2计算语义工作流的基于日志的任务执行关系getTaskRelationMatrix。

输入：语义工作流SW;

输出：语义工作流SW的任务执行关系矩阵TM。

1 foreach t1in taskSet do

2 foreach t2in taskSet do

3 if t1is the nearest common ancestor of t1,t2then

4 set(t1→Lt2),(t2←Lt1)in TM

5 if t2is the nearest common ancestor of t1,t2then

6 set (t2→Lt1),(t1←Lt2)in TM

7 if some AND-split node c∈NCis the nearest common ancestor of t1, t2then

8 set (t2||Lt1),(t2||Lt1)in TM

11 return TM1;

算法2的第1,2行中的taskSet为SW的任务节点集NT。参考文献[14]的分析结论，可以得出算法2的最坏时间复杂度为O(n4)，其中n=|NT|为语义工作流的任务节点数。

为方便进一步处理，本文将传递任务因果关系引入语义工作流的任务执行关系矩阵中，可以得到更准确的任务执行关系。伪代码如算法3所示。

算法3计算包含传递任务因果关系的任务执行关系getTaskTransRMatrix。

输入：语义工作流SW的任务执行关系矩阵TM;

输出：包含传递任务因果关系的任务执行关系矩阵TM1。

1 foreach t3in taskSet do

2 foreach t1in taskSet do

3 foreach t2in taskSet do

6 return TM1;

经分析，算法3的最坏时间复杂度为O(n3)，其中n=|NT|。

2.3 获取基于数据生成—消耗依赖的任务因果关系

为了确定存在任务因果关系或传递任务因果关系的任务节点间是否真正存在任务因果关系，本文计算任务节点间基于数据生成—消耗依赖的任务因果关系。在获得语义工作流的任务执行关系后，本文预先构造映射集合outTaskData,保存数据对象节点和生成它的任务节点，形如x,t1;构造映射集合inTaskData,保存数据对象节点和消耗它的任务节点，形如x,t2,其中x∈ND，t1,t2∈NT。然后通过遍历数据对象集合、集合outTaskData和inTaskData，得到基于数据生成—消耗依赖的任务因果关系。伪代码如算法4所示。

算法4计算基于数据生成—消耗依赖的任务因果关系getDTaskDpR。

输入：语义工作流SW的数据对象集合dataSet，集合outTaskData,inTaskData，任务执行关系矩阵TM1;

输出：基于数据生成—消耗依赖的任务因果关系集合R1。

1 R1=∅

2 foreach x in dataSet do

3 foreach t1inoutTaskData.getOutTask(x)do

4 foreach t2in inTaskData.getInTask(x)do

7 return R1;

在算法4的第2行中dataSet为SW的ND，第3行的函数getOutTask(x)用于获取生成数据对象x的任务节点集合，第4行的函数getInTask(x)用于获取消耗x的任务节点集合。设SW的任务节点数n=|NT|，任务节点能够处理的最大数据对象数为pmax，则数据对象的总数最大为pmax·|NT|=pmax·n，易得算法4的最坏时间复杂度为O(n3)。

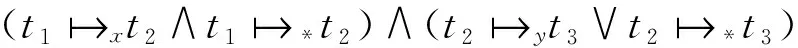
算法5计算基于数据生成—消耗依赖的传递任务因果关系getDTaskTransDpR。

输入：语义工作流SW的任务节点集合taskSet，集合R1;

输出：基于数据生成—消耗依赖的传递任务因果关系集合R2。

1 R2=∅

2 foreach t1in taskSet do

3 foreach t2in taskSet do

4 foreach t3in taskSet do

7 Return R2;

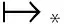
最后，遍历集合R1，R2，可以获取基于数据生成—消耗依赖的关键任务因果关系集合R3。伪代码如算法6所示。

算法6计算基于数据生成—消耗依赖的关键任务因果关系getDTaskCoreDpR。

输入：语义工作流SW的任务节点集合taskSet，集合R1,R2;

输出：基于数据生成—消耗依赖的关键任务因果关系R3。

1 R3=∅

2 foreach t1in taskSet do

3 foreach t2in taskSet do

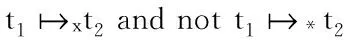
5 R3.add(t1Ct2)

6 Return R3;

在算法6的第2行中taskSet=NT。经分析，可得算法6的最坏时间复杂度为O(n2)，其中n=|NT|。

2.4 任务执行关系的更新规则

经过分析语义工作流任务节点间的数据生成—消耗依赖后，可以发现其中某些任务因果关系/传递任务因果关系仍然成立，而另一些任务因果关系/传递任务因果关系已不再成立。这是因为这些任务因果关系/传递任务因果关系所涉及的某些任务节点间不存在数据生成—消耗依赖，因而它们可以被重构到并行结构中，即将它们之间的任务执行关系更改为并行关系。于是，可得到3条任务因果关系/传递任务因果关系不再成立时的更新规则[14]，加上2条任务因果关系/传递任务因果关系仍然成立的规则，共5条更新规则，如下所示：

(1)存在数据生成—消耗依赖的任务因果关系保持不变，仍然为任务因果关系，即如果任务节点t1,t2∈NT∧t1→Lt2∧则t1,t2之间的关系保持不变，仍为t1→Lt2。

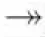
(3)将不存在数据生成—消耗依赖的任务因果关系变更为任务并行关系，即如果任务节点t1,t2∈NT∧t1→Lt2∧¬x则t1,t2之间的关系可变更为t1||Lt2。

由于t1,t2之间无数据生成—消耗依赖，则二者的执行顺序没有限制，于是可以变更t1,t2之间的关系为t1||Lt2。

解释同规则(3)。

此时，由于t2消耗了t1生成的一个数据对象，则t2可以在t1之后直接执行而不需要等待，即t1→Lt2。

第(3)～(5)条规则的严格证明过程请参见文献[14]。使用以上5条规则更新语义工作流的任务执行关系矩阵TM1，可以得到新任务执行关系矩阵TM2。

2.5 语义工作流的并行化重构

2.5.1 并行化重构算法

算法7语义工作流并行化重构算法SWPR。

输入：语义工作流SW1。

1 SW2=getReducedSWF(SW1)

2 TM1=getTaskTransRMatrix(getTaskRelationMatrix(SW2))

3 R1=getDTaskDpR(dataSet,outTaskData,inTaskData,TM1)

4 R2=getDTaskTransDpR(taskSet,R1)

5 R3=getDTaskCoreDpR(taskSet,R1,R2)

//更新SW2的任务执行关系矩阵TM1，得到TM2

6 TM2=updateTaskRMatrix(TM1,R1,R2,R3)

7 SW3=buildSWF(TM2)

8 SW3=procsSpecTask(SW3)

9 SW3=procsResConstrain(SW3,resConstrs)

10 return SW3;

算法7第7行的函数buildSWF(TM2)是对α算法[15]进行适应性改造得到的，用于根据任务执行关系矩阵TM2重构并行化后的语义工作流。此处省略伪代码。具体操作如下：

(1)由TM2中的任务因果关系→L，得到具有因果关系的任务节点对集合CT；同时得到由这些任务节点对连接生成的控制流边集合，据此初步构造语义工作流的对应图G。

(2)从某任务节点A∈NT开始遍历任务节点集合NT，逐步构造语义工作流。对于节点A，

1)如果存在节点B,C∈NT使得A→LB,A→LC且B||LC，则生成子结构，如图2a所示。

2)如果存在节点B,C∈NT使得A→LB,A→LC且B#LC，则生成子结构，如图2b所示。

3)如果存在节点B∈NT使得A→LB，且不存在满足以上两种情况的节点C∈NT存在，则生成子结构块，如图2c所示。

将以上操作得到的子结构加入图G中。

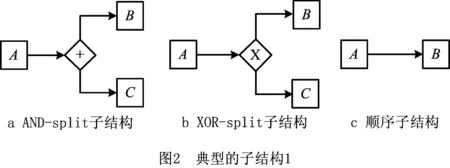
(3)从某任务节点D∈NT开始遍历任务节点集合NT，继续构造语义工作流。对于节点D。

1)如果存在节点E,F∈NT使得D→LF,E→LF且D||LE，则生成子结构，如图3a所示。

2)如果存在节点E,F∈NT使得D→LF,E→LF且D#LE，则生成子结构，如图3b所示。

3)如果存在节点E∈NT使得D→LE且不存在满足以上两种情况的节点F∈NT存在，则生成类似图2c的顺序子结构。此处不再给出图形。

将以上操作得到的子图对应的结构块加入图G中。

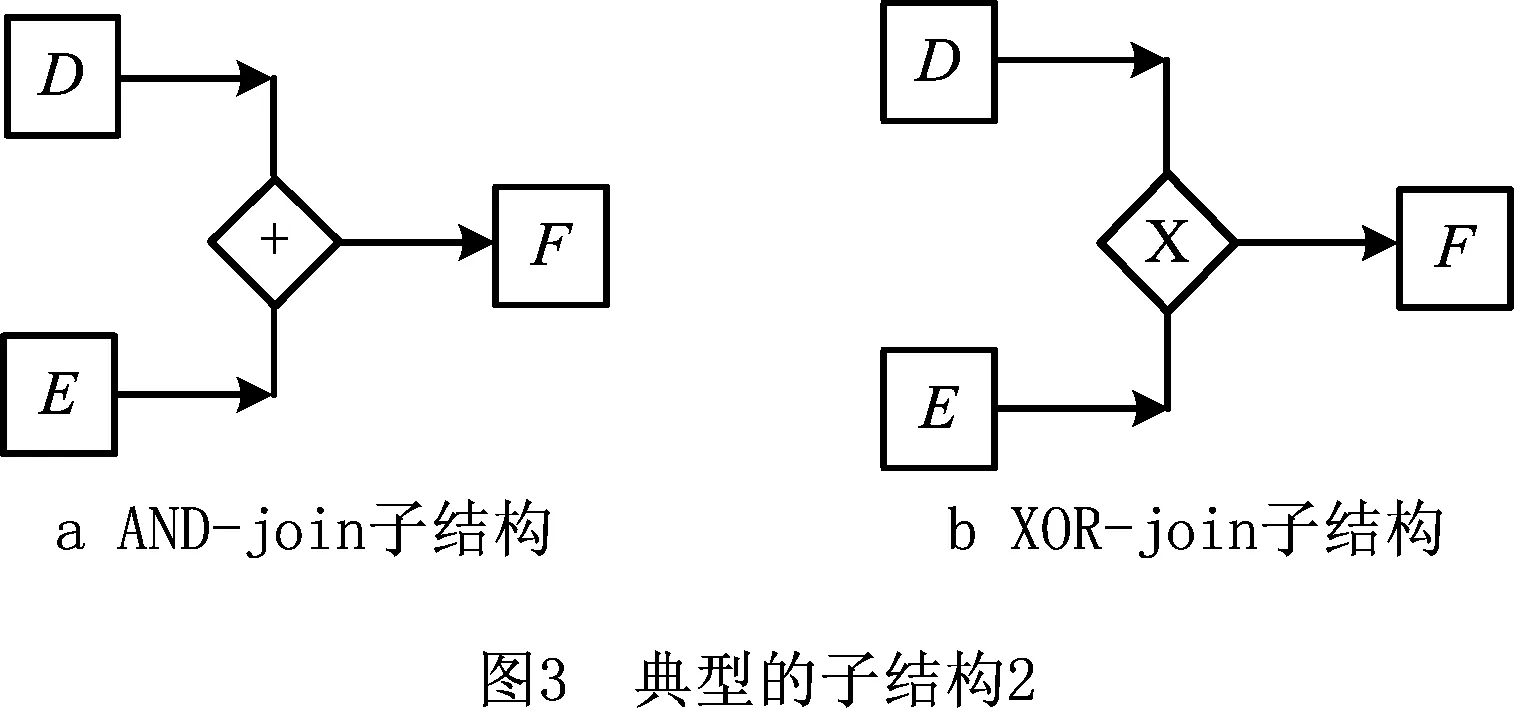
(4)对图G描述的语义工作流片段SW4进行块结构化特性检查。如果SW4为非块结构化的语义工作流，则使用最近公共前驱法、最近公共后继法重构SW4，使之块结构化。

(5)后处理操作。

遍历矩阵TM2，获得没有前驱的任务节点集合TS、没有后继的任务节点集合TF。

1)为所有没有前驱的节点Ki∈TS添加一个AND-split节点，生成子结构，表示各个分支一开始就可以并发执行，i=1,2,…,|TS|。如图4a所示。

2)为所有没有前驱的节点Pj∈TF添加一个AND-join节点，生成子结构，表示各个分支需要同步执行才可以结束，j=1,2,…,|TF|。如图4b所示。

将以上得到的子结构加入图G中，可得到图G所描述、算法7的第7行的工作流SW3。

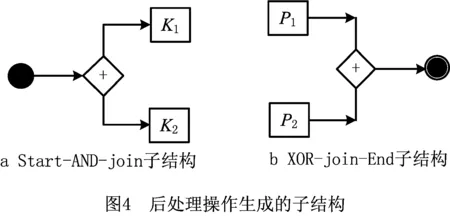
算法7第8行的函数procsSpecTask(SW3)用于对“块节点”所对应的互斥结构块和循环结构块进行并行化处理，并采用并行化后的结构块替换对应的“块节点”，具体方法见2.5.2节。第9行的函数procsResConstrain(SW3,resConstrs)用于处理可能存在的资源约束，其中resConstrs为以任务因果关系或传递因果关系形式描述的资源约束。第10行得到的SW3即为并行化重构后的最终语义工作流。

2.5.2 互斥结构块和循环结构块的并行化重构

对由“块节点”所替换的互斥结构块和循环结构块，本文采用如下并行化方法。

(1)对互斥结构块的每个互斥分支进行并行化，对循环结构块的前向分支、返回分支分别进行并行化。

(2)若互斥结构块和循环结构块的内部还嵌套了互斥结构块和循环结构块，则可以使用“块节点”替换这些内部结构块，按照步骤(1)的方法并行化后再执行步骤(2)，形成递归调用。可以设定步骤(1)和步骤(2)被递归调用的最大次数iterNum。考虑到实际的并行化重构目标往往不是最大并行化，而是满意的并行化，同时考虑到处理方法的简洁性，本文设定iterNum=1。即步骤(1)和步骤(2)最多被执行2次，其中1次为正常执行，1次为递归调用。

(3)若在互斥结构块和循环结构块中存在不可见任务[17]，由于块结构化的业务过程模型中只存在SKIP、REDO两种类型的不可见任务[17]，而不存在SWITCH类型的不可见任务。因此本文的并行化处理方法如下：

1)对于互斥结构块中SKIP类型的不可见任务，只需要进行其他分支的并行化。

2)对于循环结构块中REDO类型的不可见任务，只需要进行其他分支的并行化。

(4)经过以上并行化操作，除了“块节点”，语义工作流中的互斥结构块和循环结构块均被并行化。将得到的语义工作流中的“块节点”替换为对应的并行化前的互斥结构块和循环结构块，得到并行化重构的语义工作流。

定理1并行化重构前后语义工作流的功能一致。

证明易知，并行化重构过程可能会改变任务节点间的执行关系，而不会改变任务节点的数据消耗—生成依赖，即每个任务节点消耗和生成的数据对象保持不变。

(1)假设原语义工作流的某任务节点task1在并行化前消耗的数据对象集合为S1，由并行化重构过程可知在并行化后task1仍只消耗S1，而不会消耗其他数据对象。由此可得，并行化重构前后语义工作流在整体上所消耗的数据对象一致。

(2)将原语义工作流中由某任务节点生成但又被其他任务节点消耗的数据对象称为中间生成数据对象，将由某任务节点生成但没有被其他任务节点消耗的数据对象称为最终生成数据对象。假设原语义工作流的某任务节点task2生成了数据对象集合S2，其中包含中间生成数据对象集合S3、最终生成数据对象集合S4，S2=S3∪S4。由并行化过程可知，S3中的数据对象会被相应的任务节点消耗，而S4中的数据对象会被保留下来。遍历并行化后的语义工作流的所有任务节点，其最终生成数据对象仍可组成原语义工作流的最终生成数据对象集合。由此可得，并行化前后语义工作流的最终生成数据对象一致。

由此可知，并行化重构前后的语义工作流所消耗的数据对象、最终生成数据对象均相同，从而并行化重构前后语义工作流的功能一致。

2.6 语义工作流的并行度计算

为了评估业务过程模型的并行程度，Mendling[18]使用式(1)计算基于Petri网的业务过程模型的并行度(并发度)：

(1)

式中d(t)表示变迁节点t的出度。

若计算得TS1=-1，则令TS1=0；若TS1=0，表示该Petri网没有变迁可以并行执行。经分析发现，式(1)只关注出度大于1的变迁节点，而忽视了由该变迁节点引出的并行分支中的变迁节点。并行分支中的每个变迁都对整体并发度有贡献，忽视它们不能准确地评估业务过程模型的并行度。

本文对式(1)进行改进，使用式(2)计算语义工作流的并行度：

TS2=N1/N0。

(2)

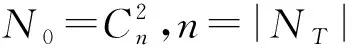
2.7 资源约束的处理方法

在业务过程模型中，资源指的是执行任务的人或物[19]。一般情况下，某一时刻一个资源只能执行一个任务。例如，在某一时刻打印机只能执行一个打印任务，只有前一个任务完成后，下一个任务才能开始。如果某个语义工作流需依赖多个资源来完成执行，则由同一资源执行的多个任务也只能顺序执行，而不能并行执行。本文称这些任务之间存在资源约束。

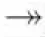
在具体语义工作流的并行化重构中，可能存在多种重构方式，将存在资源约束的并行任务节点对变更为因果关系，这样会得到多种结构形式的语义工作流，本文侧重选取并行度较高的重构语义工作流。在进行存在资源约束的语义工作流并行化时，相比不考虑资源约束，的确会部分降低语义工作流的并行度，这是在并行度和资源约束之间所做的折中。

2.8 语义工作流并行化重构实例

例2使用本文的算法SWPR对语义工作流SW2进行并行化重构。

由图5易知，SW2的并行度TS2=0。本文使用任务节点的语义描述指代该节点。为方便书写，使用大写字母A,B,…这样的标签替换这些语义描述，如表1所示。

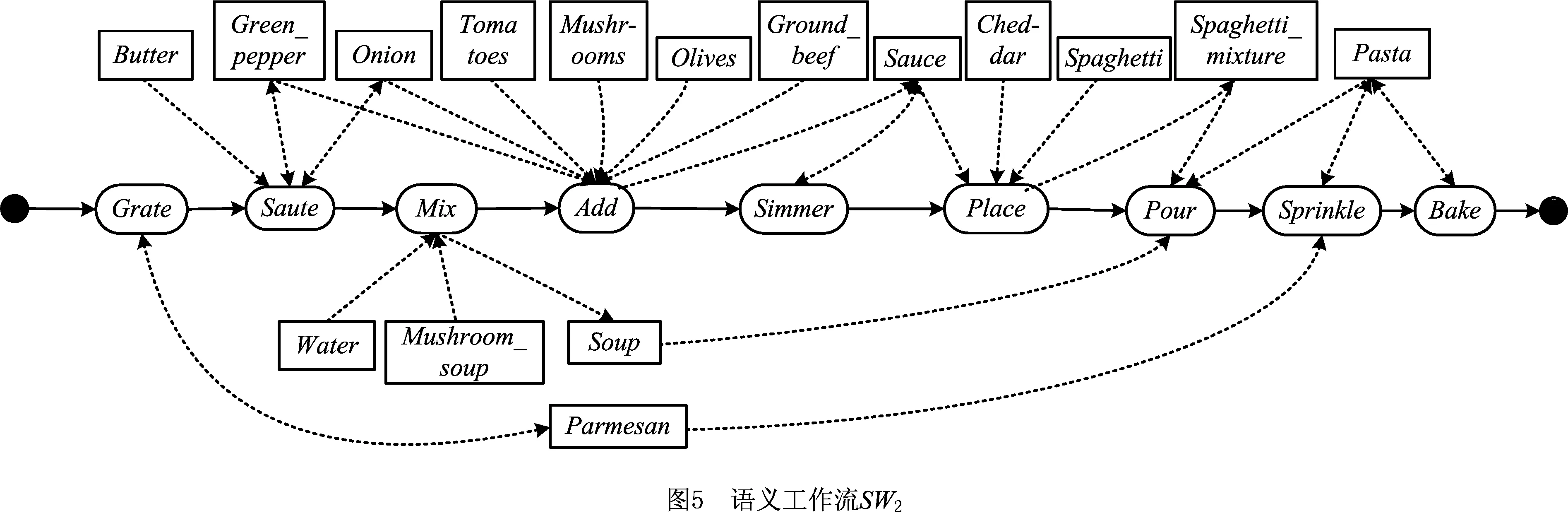
表1 SW2的任务节点语义描述的替换标签

(1)由于SW2为顺序结构，故无需化简，可以直接获取任务执行关系。根据2.2节，可以得到SW2的包含传递任务因果关系的任务执行关系矩阵TM1，如图6所示。由于TM1为对称矩阵，图6仅给出了其右上三角部分。

(2)根据2.3节，分析SW2的数据生成—消耗依赖，得到SW2的数据依赖矩阵TM2，如图7所示。进而可得基于数据依赖的传递和关键任务因果关系的数据依赖矩阵TM3，如图8所示。

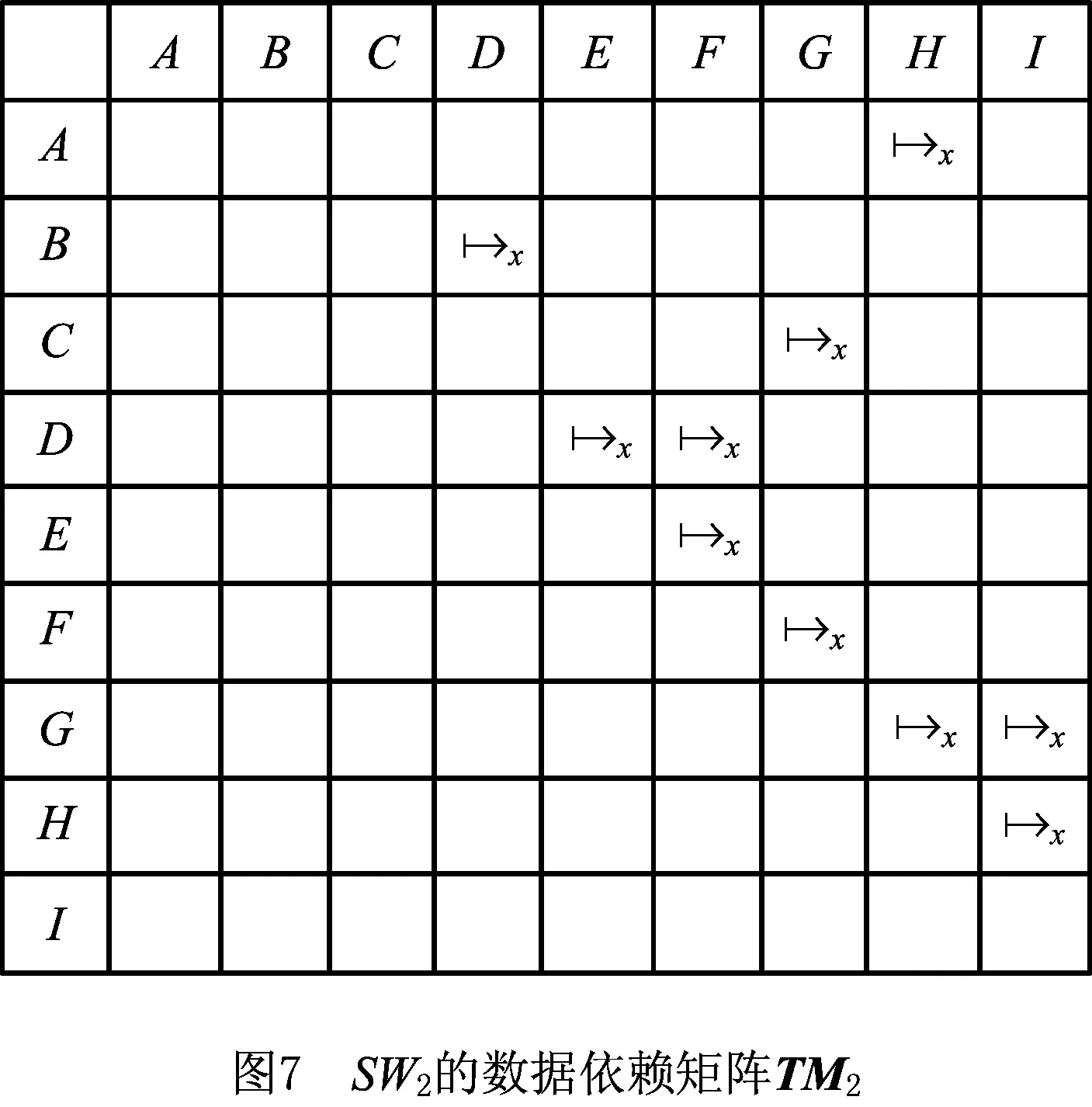
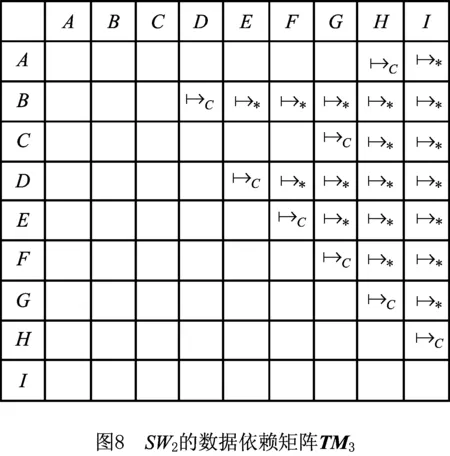
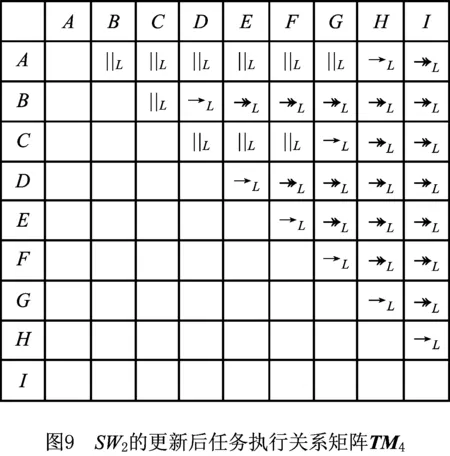
(3)依据2.4节的更新规则，得到更新后的任务执行关系矩阵TM4，如图9所示。

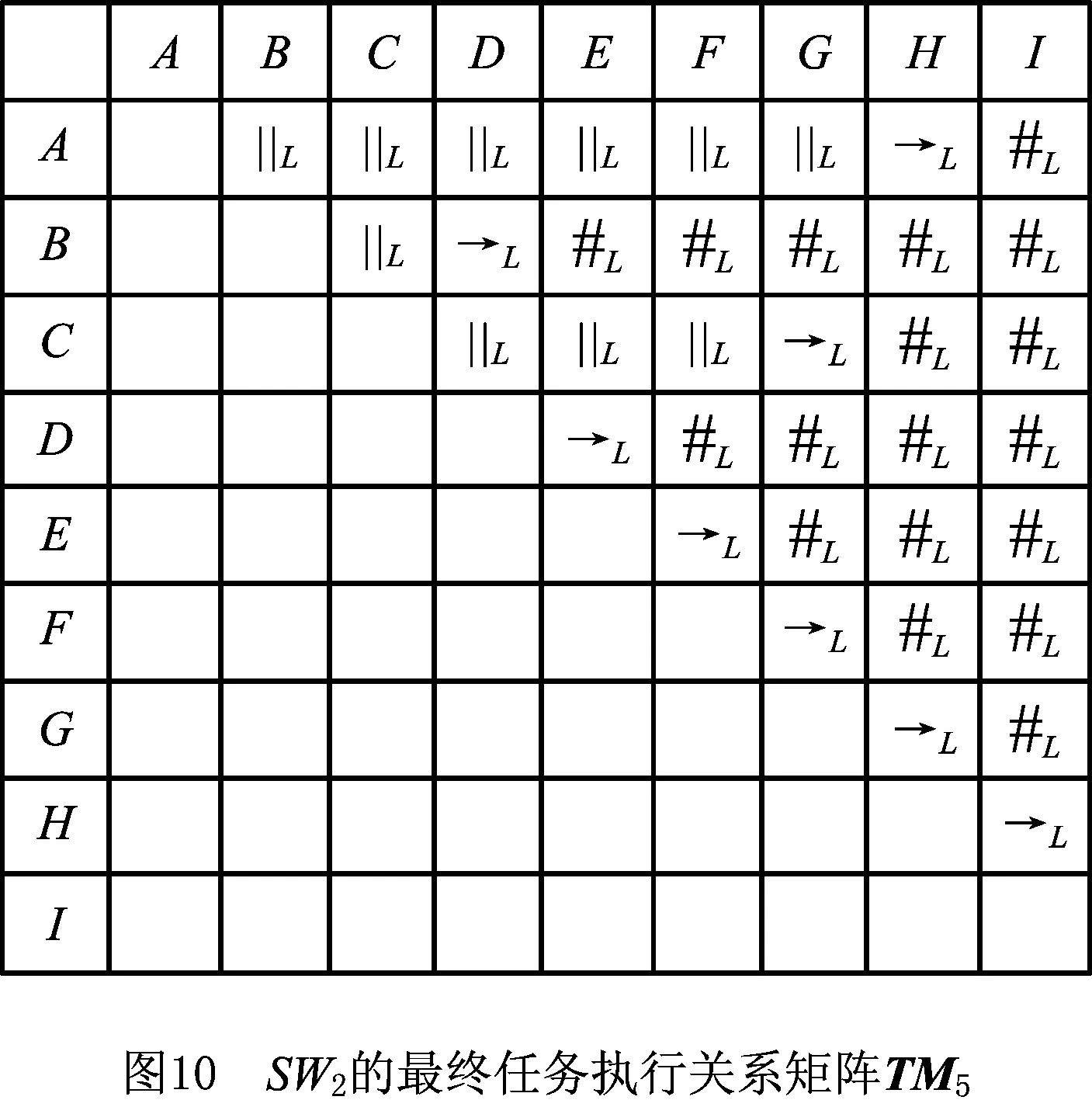
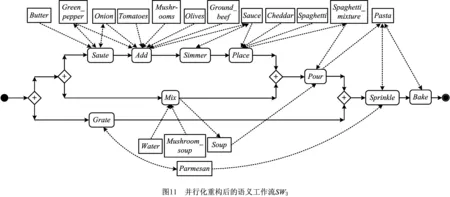
由图10，使用SWPR算法得到并行化重构后的语义工作流SW3，如图11所示。易知，SW3的并行度TS2=0.28。

(5)考虑资源约束。假设任务Grate和Mix由资源Res1执行，并要求任务Mix在Grate之后执行。根据此约束重构SW3，得到新语义工作流SW4，如图12所示。

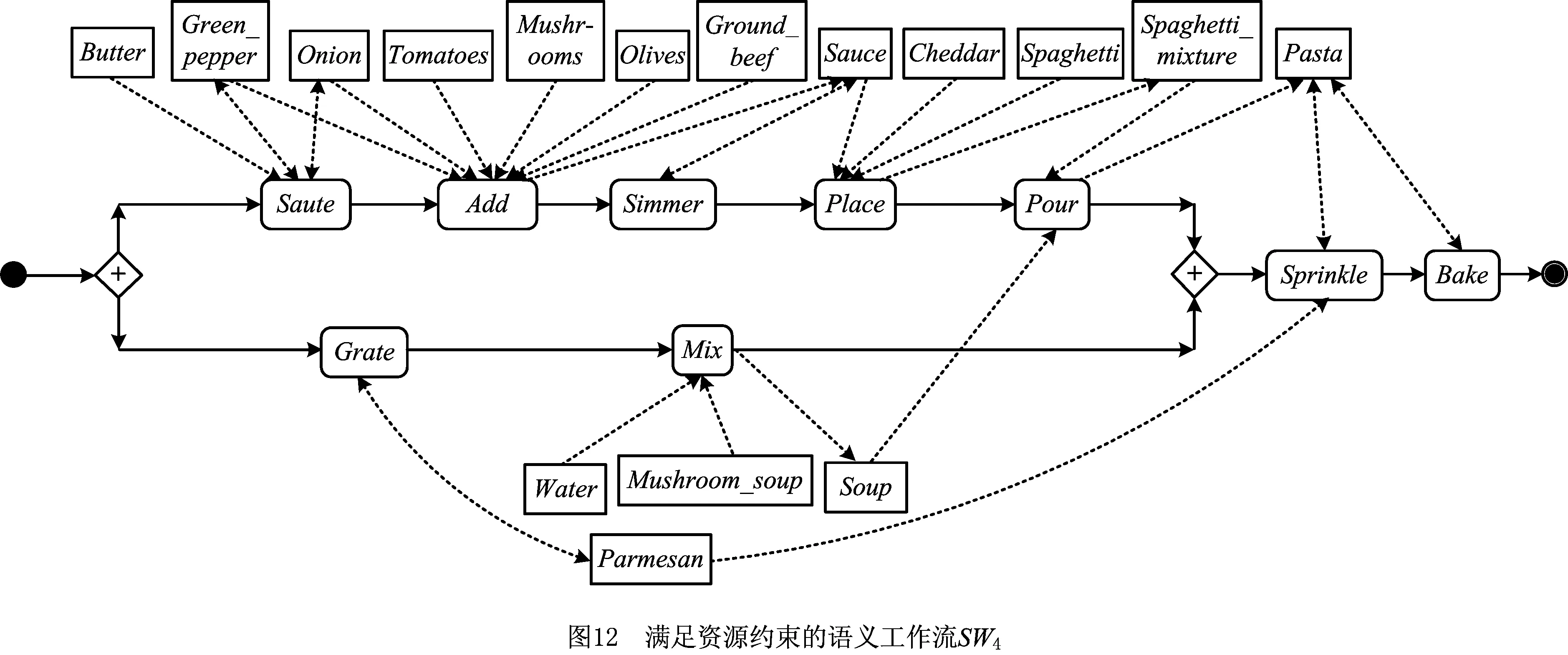
由图12易知，SW4的并行度TS2=0.28。与SW3相比，语义工作流SW4在满足资源约束的前提下保持了并行度，因此这种方式是满意的并行化重构方式。

3 实验与结果分析

3.1 并行化算法实现

为了可视化并行化算法SWPR的结果，本文开发了一个交互式的、语义工作流并行化重构软件，如图13所示。该软件的中部区域用于显示语义工作流的控制流结构，中部区域下边的标签栏用于输出所显示语义工作流的并发度TS2。左侧区域的上部显示了任务节点生成和消耗的数据对象；下部用于实现考虑资源约束时的交互功能，业务过程管理人员可以指定由同一资源执行的任务节点间的因果关系。如图13所示为图1的语义工作流SW1。

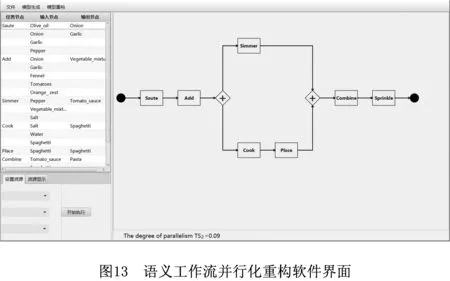
为方便语义工作流的建模与存储，本文使用XML文档保存语义工作流。SW1对应的XML文档片段如下所示。

…

…

…

SW1并行化重构后的语义工作流SW5如图14所示。

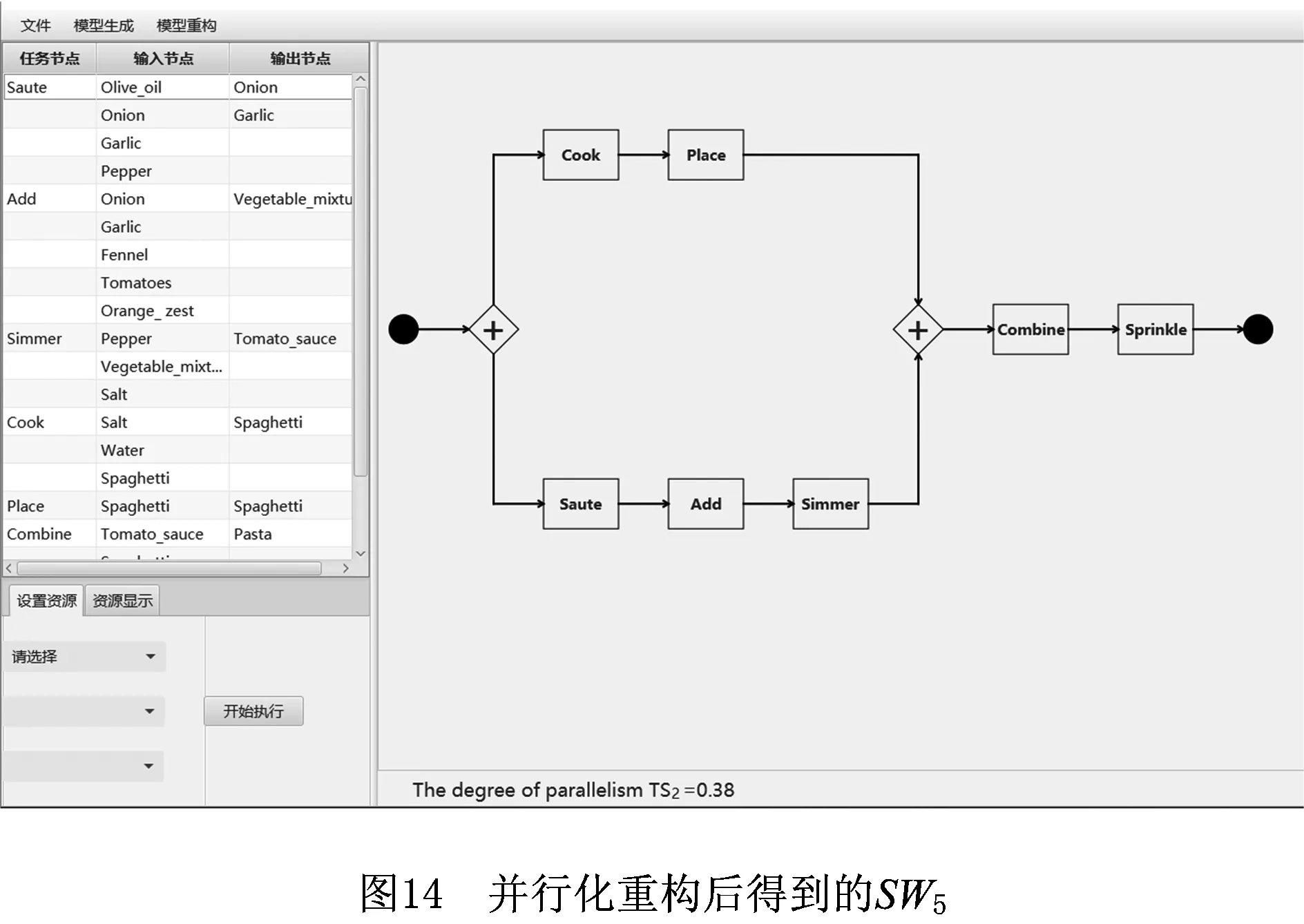
假设任务Cook和Simmer由资源Res2执行，且要求任务Simmer在Cook之后执行。根据此要求重构SW5，得到新语义工作流SW6，如图15所示。图15的左下角区域是为任务Cook和Simmer设置的资源约束，中间区域是考虑资源约束的、并行化重构后得到的语义工作流SW6。

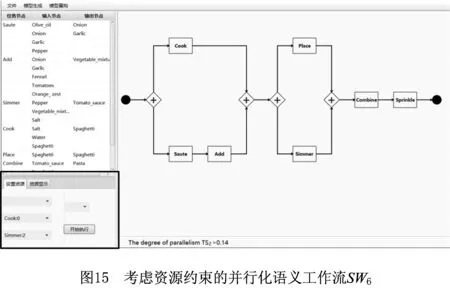
3.2 实验建立

本文实验基于如下环境：Intel(R)Core(TM)i5 2.50 GHz CPU，16.0 GBRAM，Windows1 064位操作系统，JDK1.8，JVM虚拟内存为1 G的笔记本计算机。

本文共使用4个实验数据集，其基本结构如表2所示,说明如下：

表2 数据集DS1,DS2,DS3,DS4的基本结构特征

(1)数据集DS1为了验证SWPR算法对顺序结构语义工作流的并行化有效性，同时评估其时间效率，随机生成400个顺序结构的语义工作流。Mendling[20]建议业务过程模型的任务节点最大数目不应超过50，否则需要分解[20]。因此，本文限定随机生成工作流的最大任务节点数为50，最小任务节点数为2。首先使用代码随机生成700个任务顺序执行的语义工作流，其中任务节点数n=2,3,4,…,50。为方便处理，限定每个工作流的数据对象节点最大数目为5n，使用同一个数据对象的任务节点的最大数目为n。然后从中选出400个工作流组成DS1，并确保任务节点数为n的工作流个数不少于5个，其中n=2,3,4,…,50。

(2)数据集DS2为了评估真实场景下SWPR算法对顺序结构语义工作流并行化的时间效率，手工建模50个顺序结构的食谱语义工作流。来自Recipesource(Searchable Online Archive of Recipes(SOAR), http://www.recipesource.com)，其中共有1 000多个Pasta食谱。随机选取50个Pasta食谱，手工将食谱的烹饪说明建模成如图5所示、顺序执行的语义工作流，组成DS2。

(3)数据集DS3为了评估真实场景下SWPR算法对一般结构语义工作流并行化的有效性和时间效率，手工建模50个一般结构的食谱语义工作流。来源与DS2相同。选取50个Pasta食谱，手工将每个食谱建模为一般结构的语义工作流，组成DS3。每个工作流包含顺序、并行、互斥或循环结构块，部分工作流包含不可见任务节点。

(4)数据集DS4为了验证在真实场景下SWPR算法对一般结构语义工作流并行化的时间效率，手工建模50个一般结构的、药品制备流程的语义工作流。检索专利技术文献，选取50种药物的制备流程。手工将每个流程建模成一般结构的语义工作流，组成DS4。每个工作流包含顺序、并行、互斥或循环结构，其中部分语义工作流包含不可见任务。

3.3 实验结果对比

3.3.1 有效性验证

易知，并行化前数据集DS1中每个语义工作流的TS1=0,TS2=0。使用本文的算法SWPR并行化重构DS1中的工作流。然后，分别使用式(1)和式(2)计算并行化后工作流的并行度TS1和TS2。对TS1,TS2进行统计，得出Max(TS1)=36，Min(TS1)=0，Avg(TS1)=11.25，Stdev(TS1)=9.3；Max(TS2)=1，Min(TS2)=0，Avg(TS2)=0.79，Stdev(TS2)=0.25；且TS1=0,TS2=0的工作流数量Count(TS1=0)=Count(TS2=0)=23。分别绘制工作流的TS1,TS2分布图，如图16所示。

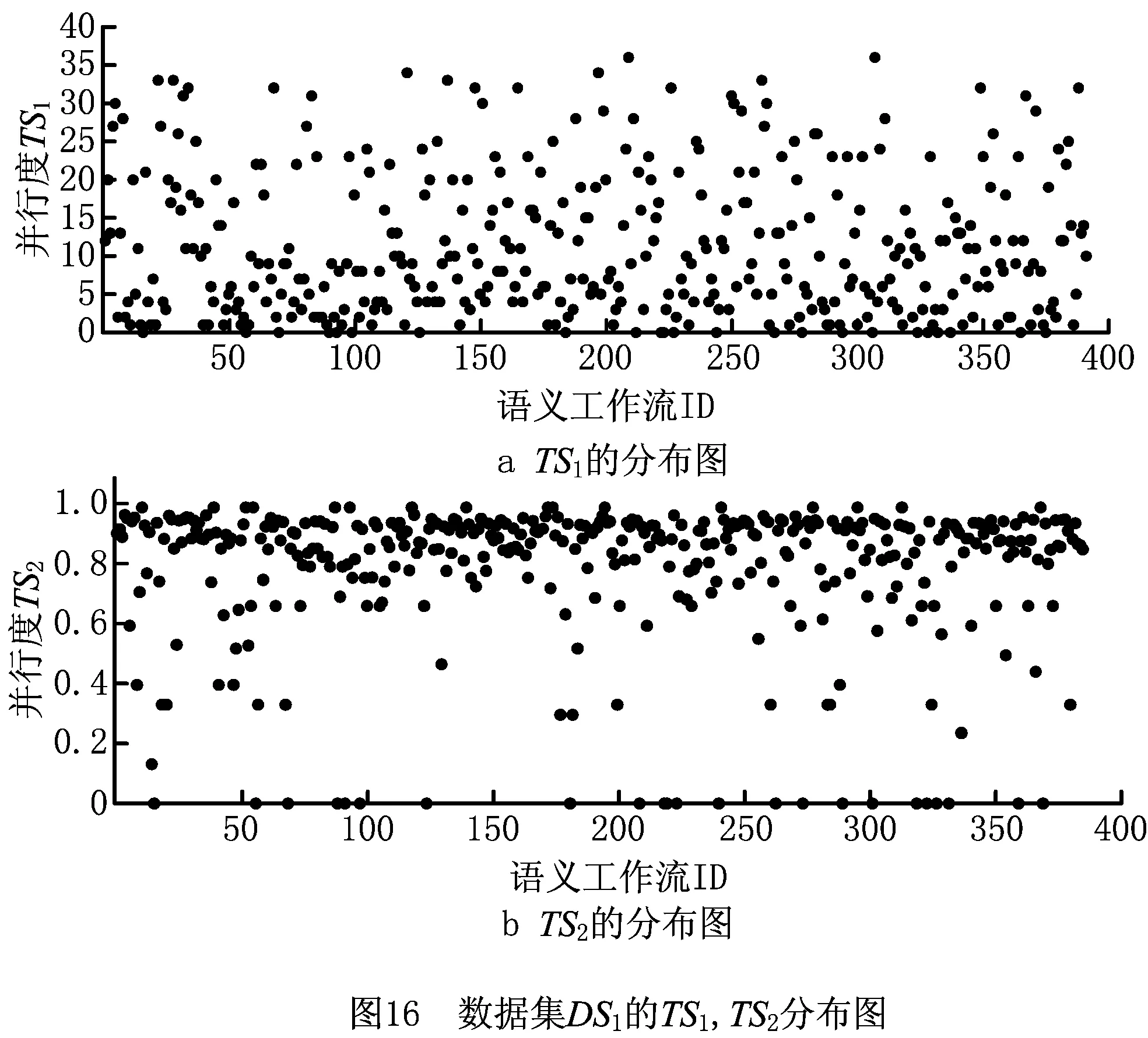
由统计数据和图16可以看出，共有377个工作流的并行度得到了提高，表明这些工作流执行了并行化重构操作。经检查，23个并行度TS1,TS2为0的工作流并不能进行并行化重构，故TS1,TS2仍保持为0。由此可以得出，本文的SWPR算法对顺序结构的语义工作流的并行化重构有效。

从数据集DS3中随机选取10个工作流组成数据集DS5，首先计算并行化前工作流的并行度TS2，然后使用SWPR算法并行化重构DS5中的每个工作流，接着计算并行化后工作流的并行度TS2。绘制并行化前后工作流的TS2分布图，如图17所示。

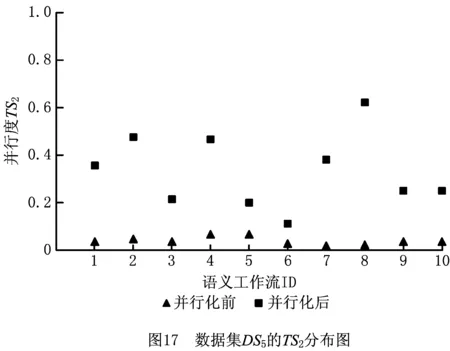
由图17可以看出，DS5中所有语义工作流的并行度均得到了提高。由此可以得出，SWPR算法对一般结构的语义工作流的并行化重构仍然有效。由以上两个实验可知，SWPR算法对语义工作流的并行化重构的确有效。

3.3.2 效率测试

使用代码将数据集DS1,DS2,DS3,DS4中的语义工作流转换成标签Petri网，为变迁节点加上输入和输出数据对象。对本文的SWPR算法进行改造，使之适用于带有生成—消耗依赖的数据对象、基于标签Petri网的业务过程模型，得到标签Petri网的并行化重构(Parallelism Refactoring for Petri Net, PNPR)算法。

对DS1中任务节点数n的语义工作流，分别使用SWPR和PNPR算法进行并行化重构，其中n=2,3,4,…,50。分别记录SWPR和PNPR算法的平均运行时间，绘制两种算法的平均时间曲线，如图18所示。

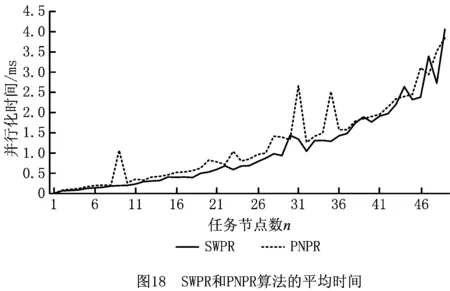
由图18可以看出，随着任务节点数n的增加，SWPR和PNPR算法的运行时间都增大较快，但SWPR算法的稳定性更好。SWPR算法的大部分曲线略低于PNPR算法的曲线，这是由于PNPR算法处理标签Petri网的库所节点占用了时间。因此有必要对SWPR和PNPR算法进行优化。

对数据集DS2,DS3,DS4分别使用SWPR，PNPR算法进行10次独立的并行化重构，记录每个数据集的每次并行化时间，然后计算每个数据集的平均并行化时间。如表3所示。

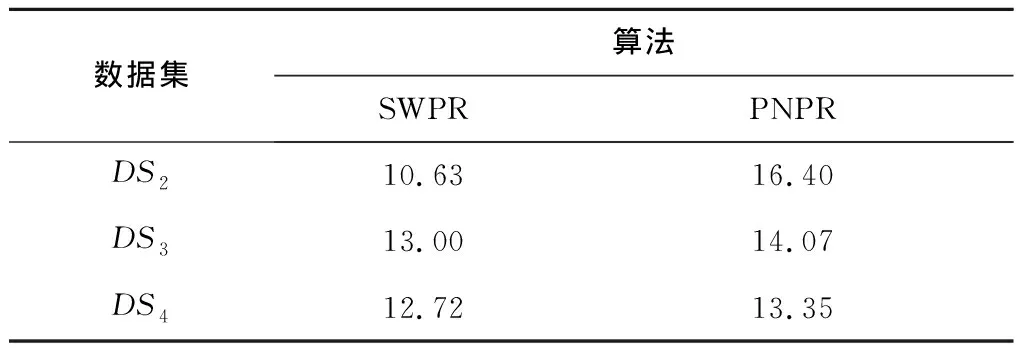
表3 数据集DS2,DS3,DS4的并行化时间 ms

由表3可以看出，对于小规模数据集，SWPR和PNPR算法的并行化重构时间可以接受。总体上，SWPR算法的并行化时间少于PNPR算法，这是由于PNPR算法还需要处理标签Petri网的库所节点，而SWPR算法不用。考虑到语义工作流并行化重构的对象一般是中小规模数据集，故基本可以接受SWPR算法的时间性能。

3.3.3 并行化重构的工作流并行度的提升倍数

从数据集DS3和DS4中随机抽取10个初始并行度不为0的工作流，组成数据集DS6，使用式(2)计算并行化前的工作流并行度。然后，使用SWPR算法进行并行化重构操作，并使用式(2)计算并行化后的工作流并行度，然后使用式(3)计算并行度提升倍数dpr：

dpr=(dp2-dp1)/dp1。

(3)

式中dp1，dp2分别为并行化前、后的工作流并行度。绘制并行度提升倍数图，如图19所示。进而，计算得DS6中工作流并行度提升倍数的平均值Avg(dpr)=9.30。由图19可以得出，对于初始并行度不为0的语义工作流，使用SWPR算法进行并行化后，相比原语义工作流，新工作流的并行度得到了较好的提高，平均并行度提升倍数较高，改善了原工作流的质量。

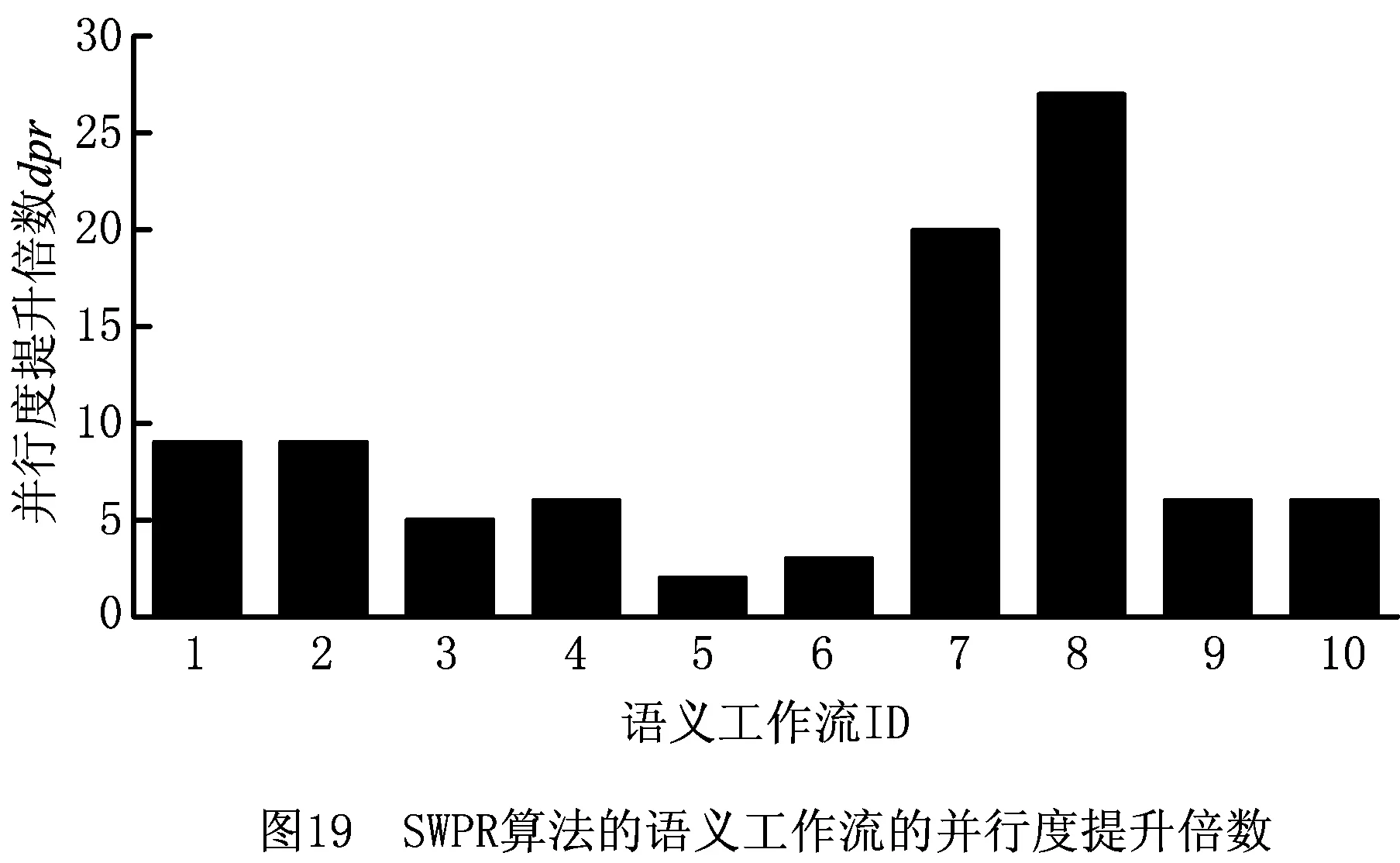
通过以上实验可知，本文的语义工作流并行化算法SWPR提高了语义工作流的并行度，使得语义工作流的质量得到了改善，对提高基于语义工作流的业务过程的运行效率有积极的支持作用。

4 结束语

针对提高语义工作流质量的需求，以及现有业务过程模型并行化方法不能处理语义工作流中数据生成—消耗依赖、资源约束等问题，本文提出一种基于数据生成—消耗依赖的语义工作流并行化重构算法SWPR。首先，使用节点编号法和最近公共前驱法获取语义工作流的任务执行关系矩阵；其次，分析了任务节点间的数据生成—消耗依赖，提出基于数据生成—消耗依赖的任务因果关系、传递任务因果关系和关键任务因果关系概念及获取方法，得出数据依赖矩阵；然后，提出5条任务执行关系更新规则，结合数据依赖矩阵来更新任务执行关系矩阵，得到基于数据依赖的任务执行关系矩阵；进一步，基于该矩阵设计了考虑资源约束的工作流重构算法以生成并行化的语义工作流；最后，提出了一种语义工作流的并行度计算方法以评估并行化后的语义工作流的并行程度，同时实现了一个基于SWPR算法的交互式语义工作流并行化重构软件。实验结果表明，本文的SWPR算法可以提高语义工作流的并行度，改善语义工作流的质量，并为提高基于语义工作流的业务过程运行效率提供了基础支持。

未来将致力于研究本文的SWPR算法的优化方法，如使用剪枝等手段减小并行化语义工作流时块结构化的检查与重构时间，进一步提高算法的运行效率；考虑OR结构块的并行化重构方法；同时考虑将本文的SWPR算法作为插件加入到PROM软件中。