基于对齐处理与偏差检测的业务流程适合度分析

张力雯，方贤文

(安徽理工大学 数学与大数据学院,安徽 淮南 232001)

1 问题的提出

1.1 研究背景

近年来，过程挖掘[1]是被广泛研究与应用的新兴技术，主要分为过程发现、服从性校验、模型完善3个阶段[2]。其中，过程发现主要集中于从日志提取与特定阶段实际运行中过程模型的行为相吻合的可执行信息[3]。通过对日志与模型的分割，使用水平与竖直两种不同的分割种类发现日志所记录的行为并建立模型[4]。但在实际中，基于一个IT系统运行日志可观测行为所建立的模型是不断变化的，在不同阶段会出现不同的变量，因此需要对模型进行监测，从而校验现有模型与日志中所记录的行为是否一致，即服从性校验。目前的研究主要从行为轮廓及日志预处理两方面来分析服从性。行为轮廓的服从性度量综合考虑执行顺序、因果耦合服从、日志服从3方面因素[5]。基于业务流程建模符号(Business Process Model Notation, BPMN)所描述模型与日志间的服从性校验方法是先对日志的单个事件与模型的单个部分进行比较，再对整体进行比较，采用从局部到全局的校验方法[6]。将日志与模型都转换成自动机，并采用A*启发式算法对两种自动机所产生的最小化修正错误进行计算，从而有助于完整的服从性校验[7]。在对服从性校验的研究中，日志与给定模型的对齐是一项重要工作。采用迹对齐的方法对事件日志进行预处理，通过分析与过滤日志，使之后的研究工作更加容易[8]，在此基础上进一步从一些异常行为中提取有效行为，从而提高服从性校验的效率[9]。

本文主要通过核算准确定位的偏差来测量适合度[10],从而进行服从性分析，在保证适合度的基础上会尽量兼顾精度,通常日志与模型之间的服从性校验还需对精度及泛化性进行权衡[11]。服从性校验的4个度量标准在文献[12]中有详细的分析。通过检测偏差、确定偏差所发生的位置及分析偏差为什么会发生来进行服从性校验，最终可以实现对模型的修复。目前，对模型修复的研究主要从服从性的4个度量标准来进行[13]，也可以基于不同特征所划分的系统进行统一框架下不同规则的比较来选择最优方法[14],或利用扩展校准的概念结合对过程树非叶子结点的查找进行高精度的模型修复[15]。实际应用中偏差检测是服从性度量的重要组成部分，将事件日志与给定模型对齐[16]，通过检测对齐所产生的偏差并根据其类型、功能性、严格性的不同划分种类[17]，结合偏差成本核算和A*算法进行服从性分析[18]。在对齐选择时，经常出现对齐偏差不同，但通过评估函数所得的对齐距离相同的情况，这时需要根据成本的大小来选择最小偏差的对齐[19]。整体对齐的偏差检测是日志与模型直接对齐，并采用检测到的偏差总成本与所有比较元素之间的比率用来测量适合度[20]，但这种方法只局限于对简单模型的分析，当面对复杂模型时会由于误差及工作量巨大而很难准确地分析服从性。本文对之前研究工作的延伸，适用于通过检测对齐偏差来处理复杂模型的服从性问题。首先，设定业务流程的选择性子路径，并以此作为约束条件，根据匹配程度的不同划分对齐；然后提出搜索最小偏差对齐的算法，通过序列比较、改进的A*算法、成本比较来层层递进地寻找最小偏差对齐，最后分析偏差回放的精度及行为关系，确定最优对齐，并根据偏差的不同种类选择相应的适合度测量公式，从而高效准确地进行服从性校验。

1.2 相关工作

目前与本文研究相关的技术主要有以下两点：①一致性校验，这种技术主要是对事件日志与过程模型之间的各种性能进行度量。文献[12]从适合度、精度、简化度、泛化度4个不同的方面判定日志与模型之间是否一致，其中最为重要的是适合度测量。一致性校验可以被应用于不同的设置中，主要包括合规性审计、模型维护以及自动化的过程发现。合规性审计只可以检测出事件日志无法回放于过程模型的行为，即不适合行为;模型维护是检测所有偏差行为的设置，既可以诊断出事件日志无法回放于模型的行为也可以发现模型中所特有的行为，即不适合行为与额外行为。自动化的过程发现是根据一致性校验的输出结果对过程模型进行调整，通过减少日志中没有记录但模型中可以捕获的行为或者增加仅日志中可观测的行为来实现对初始模型的自动化调整。②成本核算，也就是对事件日志与过程模型之间同步对齐与异步对齐的成本进行核算。通常设定同步移动的成本为0，而异步移动的成本为1(异步移动中含有不可视变迁时，成本为0)。本文根据活动在一个业务流程中所扮演角色的重要性将它们的单位成本设置为不同的值，因此一个异步移动的成本需根据其中所包含活动的不同单位成本来设定。本文与文献[17-20]中所做的工作密切相连，将日志与模型直接进行对齐比较，通过计算偏差总成本及所有对齐元素来进行适合度分析。这种方法使得服从性校验的工作仅局限于简单模型或者单个运行实例中而无法对复杂模型进行分析的情况。针对这些问题，本文通过划分强制性子序列和选择性子序列寻找事件日志与过程模型之间的最优对齐，从而在提升适合度的同时减少工作量。

1.3 动机案例

人身保险是当今社会常见的保险类型，本文使用人身保险的投保流程作为研究案例来分析所提出的方法，如图1所示为人身保险投保流程案例的给定模型M。

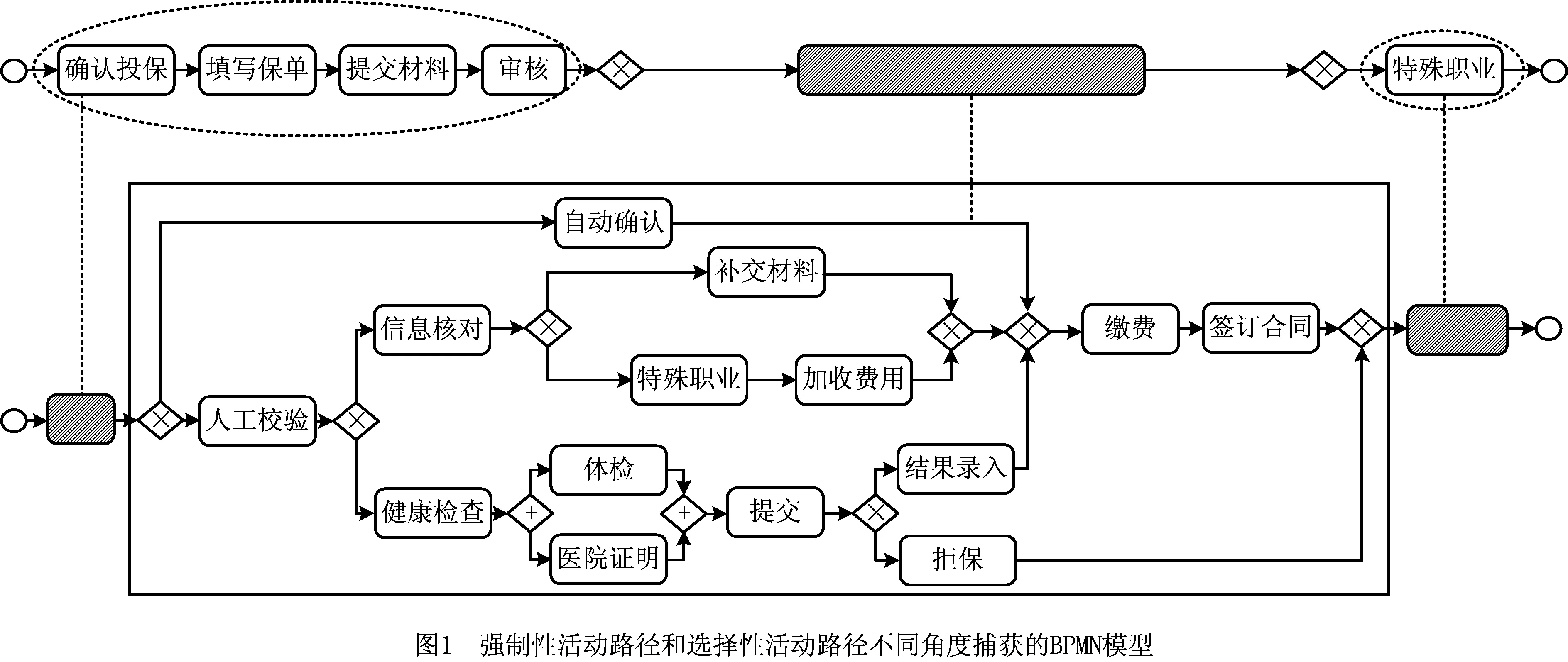
根据所有活动对业务流程运行影响程度的不同，将活动划分为两类：①强制性活动，即在任何情况下都一定会发生的活动；②选择性活动，即仅在某些情况下发生的个性化活动。将日志与给定模型中所有选择性的活动定义为参考活动。图1中分别从强制路径和选择路径的不同角度来捕获BPMN模型。根据各活动表示的活动标签在业务流程中所扮演角色的重要性不同，可将它们产生的偏差成本分别设置为：强制性活动成本为1，高级参考活动成本为0.8，低级参考活动成本设置为0.5。图1中人身保险投保流程的初始事件日志如表1所示，将该日志与图1所示的过程模型进行比较，可以看出它们之间存在差异。

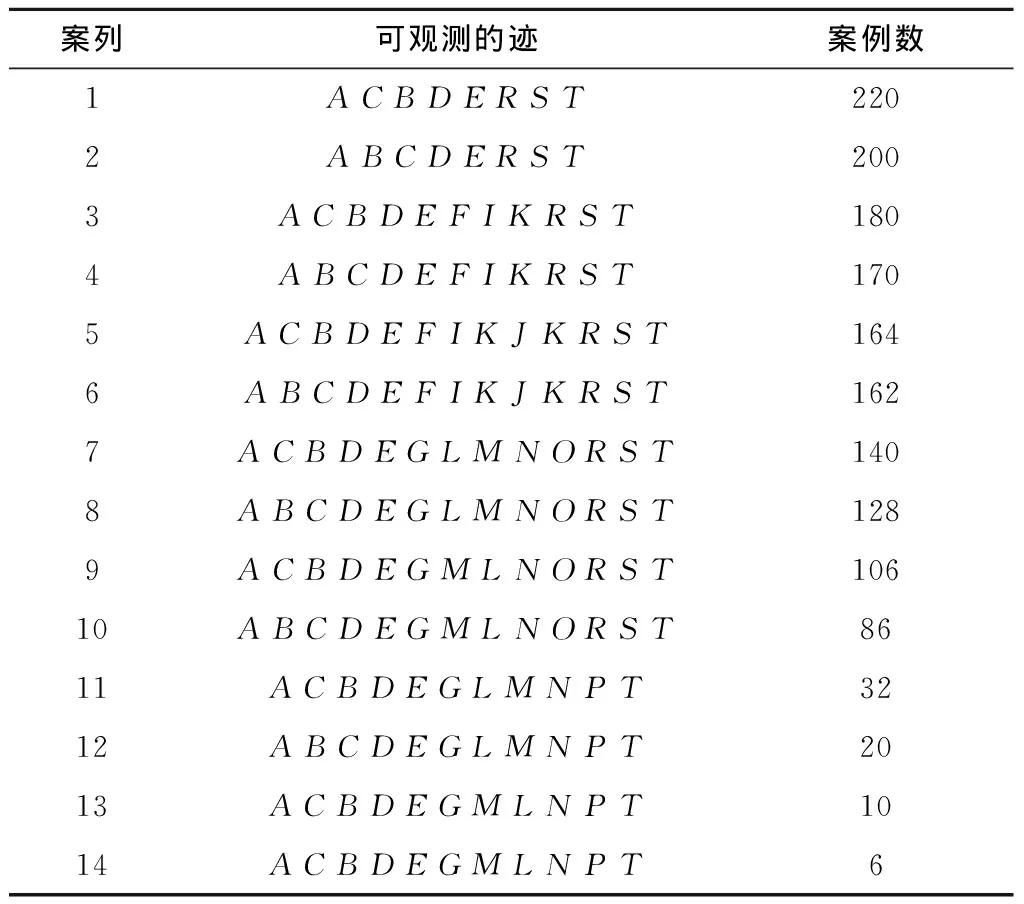
表1 人身保险投保的事件日志

2 基本概念

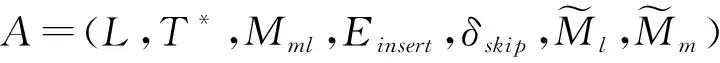
(1)对齐中非同步移动的不恰当描述，如(b,→),(→,c)不可以表示为(b,c)。

(2)在对齐中的无效对齐形式，如(→,→)，将日志与模型之间的同步非移动对齐。

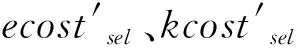
Ecost(Ec,δj)=((ecostman(∂(einsert))·ζ/ecostsel

Kcost(Ec,δj)=((kcostman(σ(tskip))·ζ/kcostsel

Ccost(Ec,δj)=Ecost(Ec,δj)/Kcost(Ec,δj)。

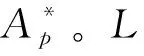
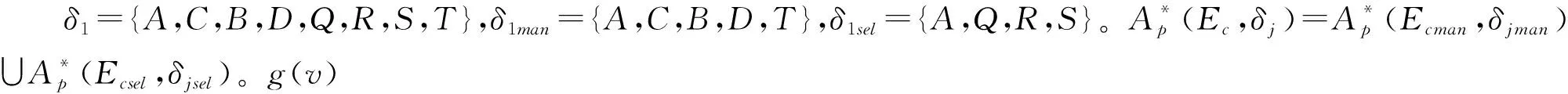
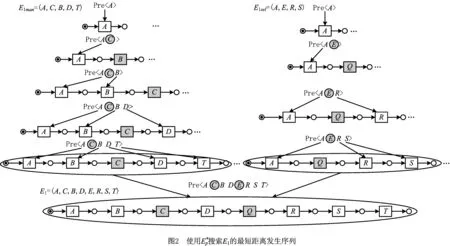
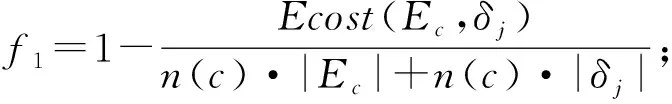
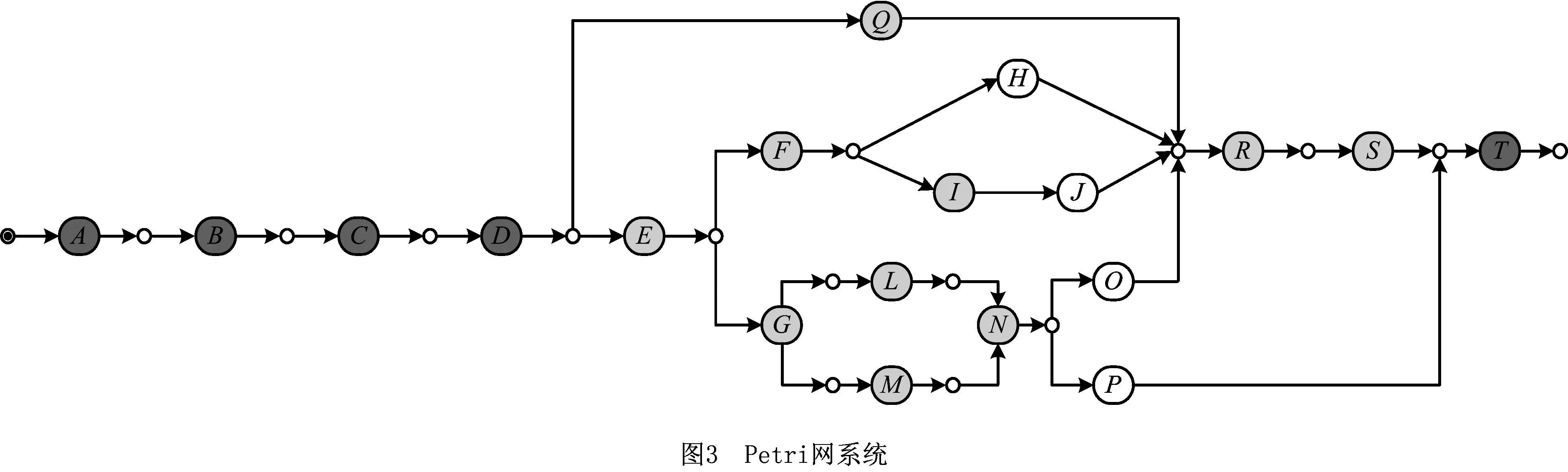
为方便起见，后文将采用Petri网的形式进行分析。由于网N的初始库所中有一个标识，在图3中将其称作Petri网系统。

3 业务流程中日志与模型的对齐搜索算法

本章介绍一种新的算法来搜索日志与模型之间的最小偏差对齐，首先给出以下3种对齐类型：①执行序列与发生序列完全相同的对齐；②选择子序列相同的对齐；③选择子序列不同的对齐。根据这3种对齐的类型可以进行搜索并层层排除，找到最小偏差的对齐。

对齐搜索算法主要分为3步：

(1)比较日志上的所有执行序列与模型中的一条发生序列，选择可以回放的执行序列添加到等价日志Eq(L)(算法1中：2～7)，依次与所有发生序列进行比较(算法1中：1～8)，将等价日志从日志中移除(算法1中：11)。

(2)设定模型与日志的参考活动，即所有选择路径上的活动Vm(算法1中：9)，由映射函数RN将Ec与δj指定为仅包含各自参考活动的选择子序列(算法1中：10)，比较剩余日志L′中所有执行序列与模型上一条发生序列的选择子序列，若存在选择子序列相同的对齐，则将该条执行序列添加到选择子序列相同日志RS(L),并添加对齐到对齐集Align*(算法1中：13～19)，依次与所有发生序列相比较(算法1中：12～20),从子日志中移除选择子序列相同日志RS(L)(算法1中：21)。

算法的返回结果是选择子序列匹配的对齐、选择子序列不匹配的最短距离或最小偏差对齐:Align*(算法1中：32)。以下为对齐搜索算法的伪代码：

算法1A ligning Search。

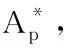
结果: set of alignment Align*。

1 for j=1, j≤|J|,j++ do

2 for c=1,c≤|C|, c++ do

3 γ(Ec,δj)

4 if Ec≡δjthen

5 Eq(L)←Ec

6 end

7 end

8 end

9 v∈V,vm∈Vm,vs∈Vs;v≫VmandVs=VVm

10 RN:Ec→Vs,Tj→Vs

11 L′=LEq(L);L←L′;

12 for j=1,j≤|J|, j++do

13 for c=1,c≤|C|, c++ do

14 γ(RN(Ec),RN(δj))

15 if RN(Ec)≡RN(δj) then

16 RS(L)←Ec

17 Align*←align(Ec,δj)

18 end

19 end

20 end

21 L″=L′RS(L);L′←L″;

22 for c=1,c≤|C|,c++ do

26 Align*←align(Ec,δsd)

27 else

28 λ(Ccost(Ec,δsd))=Ccost*(Ec,δsd)

29 Align*←align(Ec,δsd)

30 end

31 end

32 return Align*

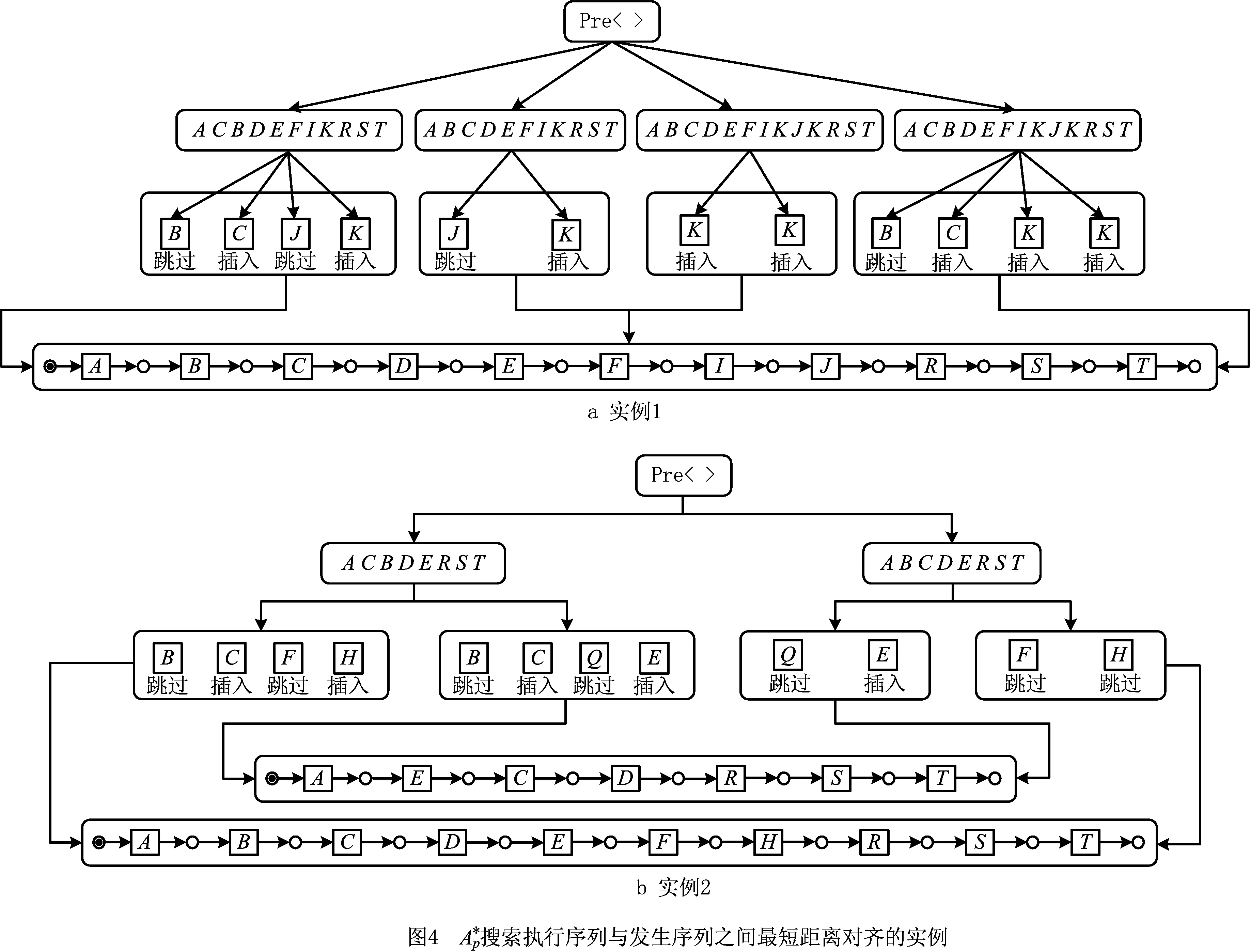
根据对齐搜索的算法分析本文给出的日志及预定义模型，图4的两个搜索案例得出L″中每个执行序列最短距离对齐的发生序列或者发生序列集。图4a中的4个执行序列搜索出同一条最短距离对齐的发生序列，而图4b中的每条执行序列则分别搜索到两条同样满足最短距离对齐的发生序列，这里需要进行偏差成本的比较来选择每条执行序列最小偏差对齐的发生序列。首先确定它们的偏差，其中E2与δ1、δ2的对齐所产生的偏差分别为：(Q,E)和(F,H)，根据定义2偏差成本的计算公式可知:

Ccost(a)=(ecostsel(E)·ζ+

kcostsel(Q)·ζ)·200=320，

Kcost(b)=(kcostsel(F)·ζ+

由成本大小选择E2最小偏差对齐的发生序列为δ2，该结论同样适用于E1。

4 业务流程的服从性校验

4.1 日志与模型的最优对齐

下面基于搜索到的最小偏差对齐作进一步处理，以获得最适合进行服从性度量的最优对齐，根据目前所有对齐的类型不同对它们进行分析。

4.1.1 偏差的精度分析

图5以实线和虚线描绘同样的偏差如何以不同的形式回放到相应的模型子模块上。通常在模型上回放日志中所记录行为的同时，应尽可能避免过多的不可见行为而使精度值下降，例如，图5中实线部分所描绘的回放行为只考虑适应度而使精度受到一定的影响，虚线部分是对其的一种改进形式。由于B、C两个元素为并发的行为关系，将它们的任一偏序均看成一个整体，即(BC)、(CB)各表示一个元素，本文用X、Y来表示，其成本分别定义为1。由此，得到一组新的对齐：

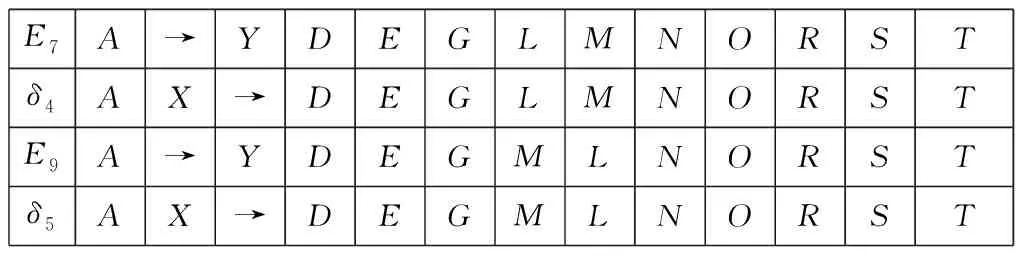
E7A→YDEGLMNORSTδ4AX→DEGLMNORSTE9A→YDEGMLNORSTδ5AX→DEGMLNORST

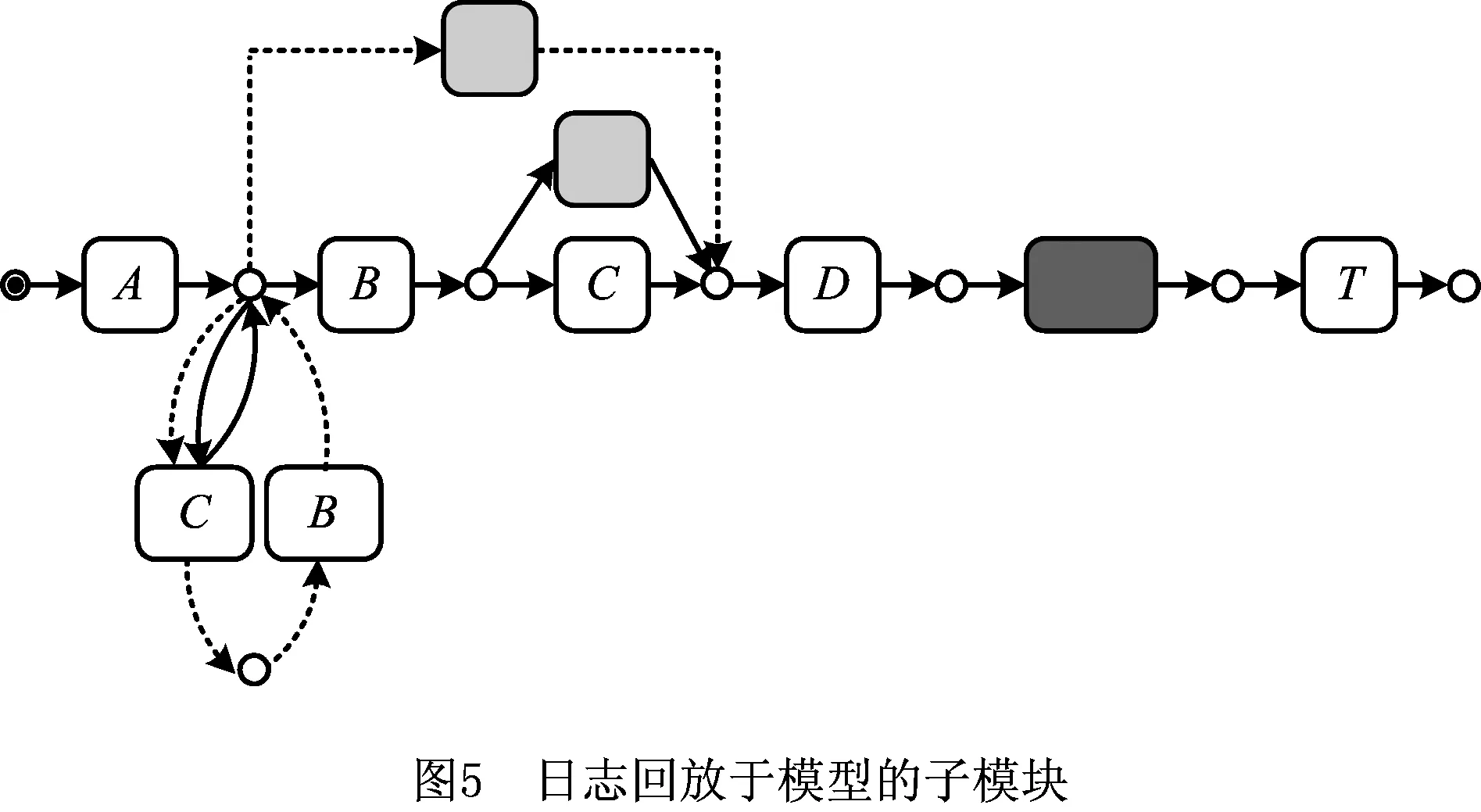
根据定义4中精度的测量公式：

可得，图4中实线部分回放后子模块的精度为0.91，虚线部分回放后的精度为1，因此选择后一种偏差形式的对齐进行服从性校验，该方法同样适用于(E11,δ6),(E13,δ7)的分析。

4.1.2 偏差回放的行为包含

根据图4a和图4b搜索出的最短距离对齐，可知图4b进行偏差成本比较之后，实现了最小偏差的唯一对齐，这里不考虑并发结构偏序的不一致。下面对图4a的对齐作进一步处理。图6中分别使用实线和虚线描述一个偏差以不同形式回放于模型所得到的子模块。将对齐的最短距离都为2的一组执行序列(E4,E6)中选择子序列不一致的部分回放于模型进行比较，图6中回放于模型上的行为可以包含E4的回放行为，因此本文选择对齐(b2)用作服从性分析。由于E6中的偏差为(K,K)，E4的偏差为(K,J)，则E6的偏差更集中，则成本更低，cost(τ)=0。由定义2的偏差成本计算公式比较对齐a2、b2的偏差成本分别为：

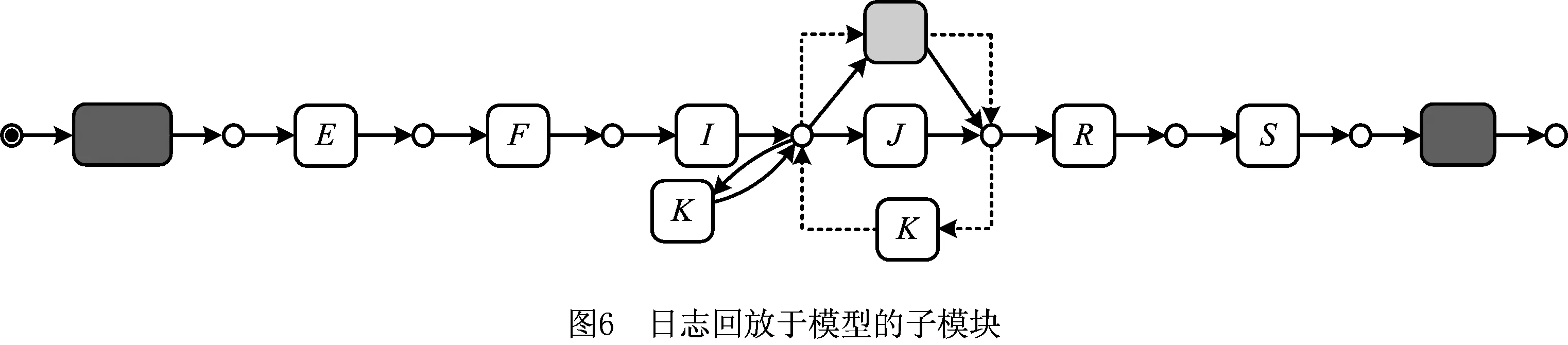
将含有并发模式的两条可回放执行序列中不同偏序的对齐看作一个整体，合并其各自的运行次数。最终得到的对齐是日志L与模型M之间的最优对齐，下面列出这些对齐,并记录对齐比较的次数：

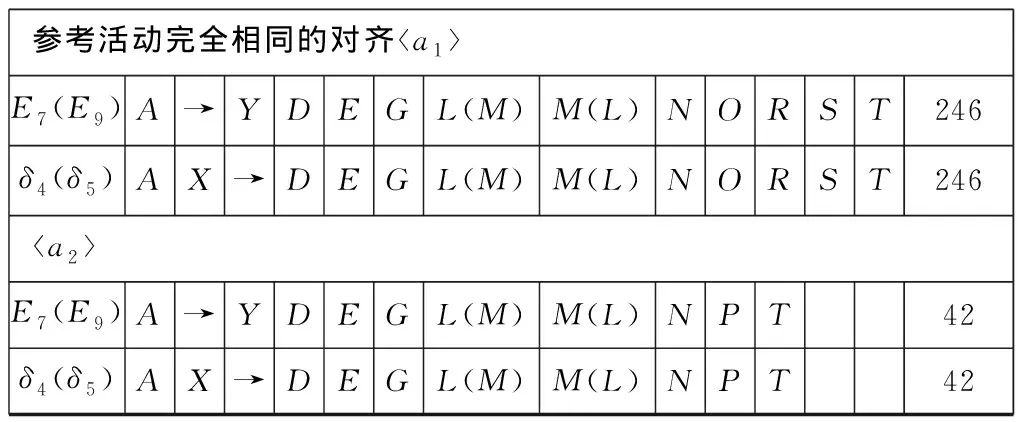
a1E7(E9)A→YDEGL(M)M(L)NORST246δ4(δ5)AX→DEGL(M)M(L)NORST246a2E7(E9)A→YDEGL(M)M(L)NPT42δ4(δ5)AX→DEGL(M)M(L)NPT42

b1E1A→YDE→→RSST220

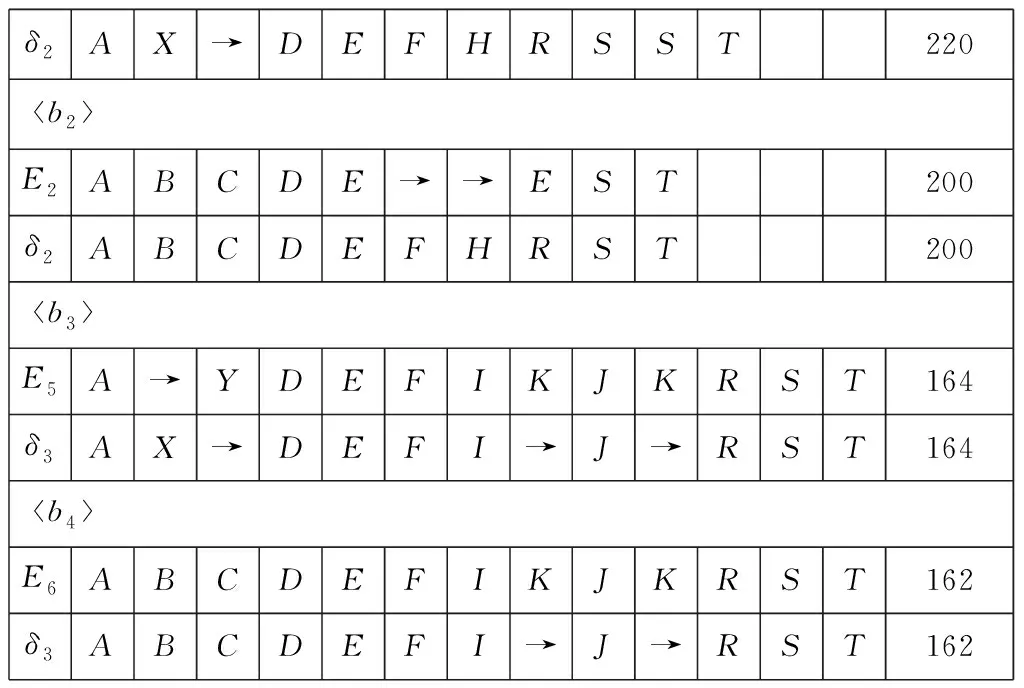
δ2AX→DEFHRSST220b2E2ABCDE→→EST200δ2ABCDEFHRST200b3E5A→YDEFIKJKRST164δ3AX→DEFI→J→RST164b4E6ABCDEFIKJKRST162δ3ABCDEFI→J→RST162

4.2 服从性校验

由上述分析得到了6组最优对齐，根据这些对齐所产生的偏差，利用定义4所给出的适合度测量公式进行校验。下面给出基于不同偏差类型的适合度公式选择规则：①对齐的不一致仅由日志L的插入偏差引起，选择f1；②对齐的不一致仅由网N的跳过偏差引起，选择f2；③对齐的不一致由日志插入和网N跳过的偏差共同引起，选择f3。分析上述最好对齐可知：a1、a2两组对齐的不一致由日志插入CB和网N跳过BC的偏差共同引起，根据规则3选择f3进行测量；b1、b2两组对齐的不一致仅由网N跳过的偏差引起，根据规则②选择f2进行测量；b3、b4两组对齐的不一致仅由日志插入的偏差引起，根据规则1选择f1进行测量;因此，日志与模型之间的适合度：

5 实验评估

本文所提方法对于改善服从性校验的性能及减少工作量的耗费都是高效可行的。本章对该方法进行实验评估，介绍实验的设置并对实验结果进行总结。

5.1 实验设置

应用本方法来分析文中给定的人身保险投保流程案例。在给定日志L和模型M上进行实验。使用文中给出的对齐处理方法搜索到最优对齐，实现将所有日志中无法回放于模型的执行序列以一对一的形式与模型中相对应的发生序列进行精准对齐，按照选择子序列是否相同依次记作：(E7(E9),δ4(δ5))、(E11(c13),δ6(δ7))、(E1,δ3)、(E2,δ3)、(E5,δ4)、(E6,δ4)。筛选出的最优对齐执行序列与发生序列进行服从性度量，其大小分别为：(3 198，3 198)；(462，462)；(1 760，2 200)；(1 600，2 000)；(2 132，1 804)，(2 106，1 782)。

5.2 实验结果分析

5.2.1 仿真实验

使用不同方法对齐事件日志与过程模型，并通过一致性校验其适合度。由于整体对齐是将事件日志中的每条序列都与过程模型的所有发生序列进行对比，其中会包含很多冗余的偏差，并造成巨大的工作量。本文采用算法1所介绍的方法搜索事件日志与过程模型之间的最优对齐，在改善适合度与减少工作量两方面对现存方法进行改进。图7是对本文方法与比较方法分别测量的适合度值进行比较的仿真结果。

5.2.2 结果评估

通过实验结果可以进行两种方法的最终评估，如表2和表3所示。

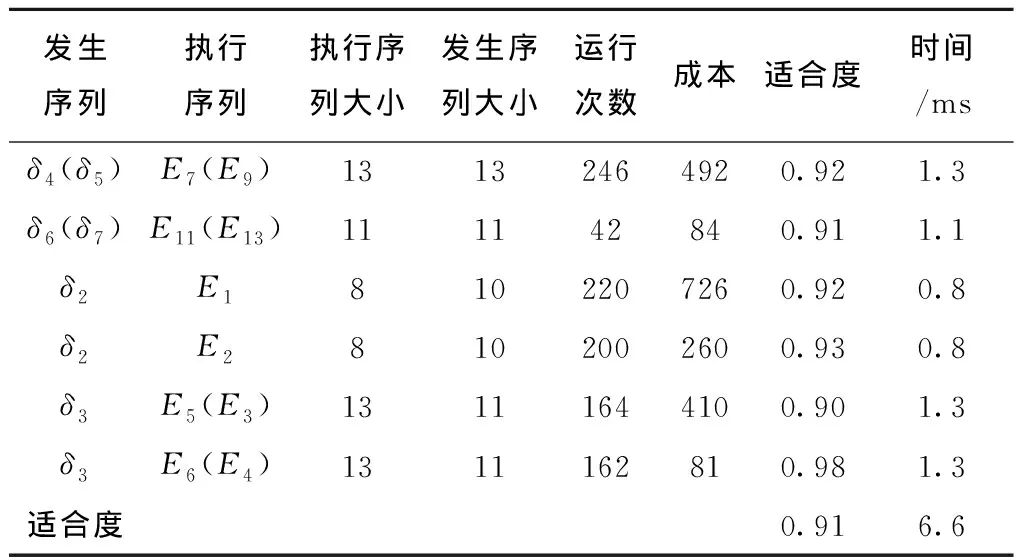
表2 本文方法的评估数据

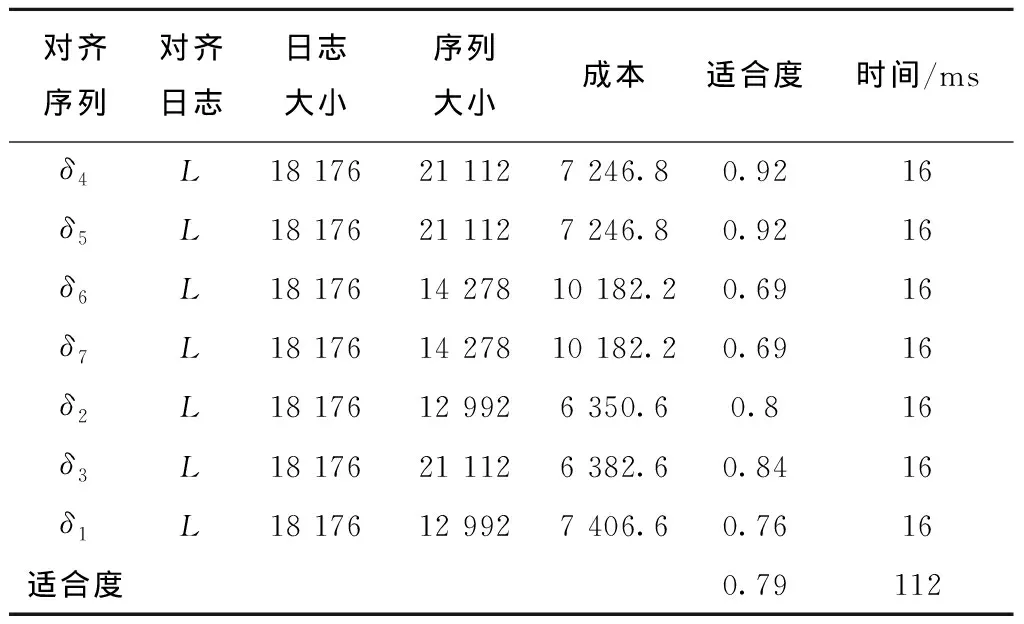
表3 比较方法的评估数据

从表2和表3中的评估数据可以清楚地看出，本文的方法较之前的方法明显提升了适合度的测量值，且由于对齐比较范围的缩小，使得计算所耗费的工作量大大减少。实验结果表明，本文的方法可行且有效。

6 结束语

通过对齐处理精准检测到的偏差可以为后续模型修复的工作提供支持。在本文的研究之上，未来可以通过对偏差进行深入分析，发现偏差如何回放于模型最合适，从而找到模型的最优修复方法。