基于相关向量机的光伏系统谐波发射水平评估方法

潘 玲， 潘爱强， 熊 敏， 张 鹏, 杨洪耕*

(1.国网上海市电力公司电力科学研究院，上海 200437；2.四川大学电气工程学院，成都 610065)

光伏系统接入城市配电网，由于城市配电网的电缆化率高，感容耦合易引发谐振问题[1-4]。光伏电站是多逆变器并网系统，光伏接入使得公共连接点(point of common coupling，PCC)电压波形畸变。城市配电网中非线性负荷和光伏系统共同导致PCC处电压畸变。评估光伏系统在PCC处的谐波发射水平，对明确光伏与背景的谐波责任，研究治理措施与制定谐波污染奖惩机制具有指导意义[5-9]。

评估谐波发射水平的方法主要有波动量法[10-11]、线性回归法[12]、协方差方法[13]等。其中，波动量法是根据PCC处谐波电压、电流波动量比值实部符号判别系统谐波阻抗，该方法虽然被广泛应用，但其筛选样本点不完备；线性回归法是通过求解方程回归系数计算系统谐波阻抗，在背景谐波波动较小条件下适用；协方差法是根据PCC处谐波电流与背景谐波近似独立协方差为零来计算系统谐波阻抗。评估光伏系统谐波发射水平时，配网中大量非线性负荷作为背景，PCC处谐波电流与背景谐波相关性增强，导致计算结果误差较大。

文献[14]提出了基于VC理论和结构风险最小化原理的方法，以PCC处测量数据作为输入向量，根据支持向量机(support vector machine，SVM)回归模型求出系统谐波阻抗。解决了非线性、小样本等问题，计算结果有较高的精度。但设置参数时，未考虑输入样本个体差异对计算结果的影响。针对这一问题，文献[15]提出了加权支持向量机回归方法，利用欧几里得距离作为权重系数评判标准，确定误差要求和惩罚参数的权系数，具有更高的计算精度。但SVM算法的稀疏性不足，随着训练样本量增加，支持向量数量增加，计算量和计算复杂度加大。并且核函数需要满足Mercer条件，SVM模型参数的确定使计算更为复杂[16-17]。文献[18]在支持向量机的基础上，提出了一种基于贝叶斯推理的相关向量机(relevant vector machine，RVM)学习方法，克服了以上问题。

基于此，提出一种基于相关向量机回归的光伏系统谐波发射水平评估方法，建立光伏电站的诺顿等效电路[18]，将PCC处谐波电压、电流数据作为输入向量，利用相关向量机回归模型得到系统谐波阻抗，求出谐波发射水平。

1 基本原理

光伏系统的并网结构如图1所示，光伏阵列的直流电能经直流侧电容连接到相应的LCL型并网逆变器，通过集电线路汇集，由升压变压器升压后，经过长线路传输后接入城市配电网。并网逆变器向电网注入大量的谐波，主要有死区时间导致的低次谐波和脉宽调制过程产生的高次谐波。并网逆变器工作时呈现出电流源性质，光伏系统中逆变器并联运行，因此将光伏系统谐波模型等效为诺顿电路。并网逆变器产生的谐波等效为光伏谐波电流源，逆变器出口至PCC之间的元件的谐波阻抗等效为光伏侧谐波阻抗。计算系统谐波阻抗的等效电路如图2所示。

图1 光伏系统并网模型Fig.1 Grid-connected photovoltaic system model

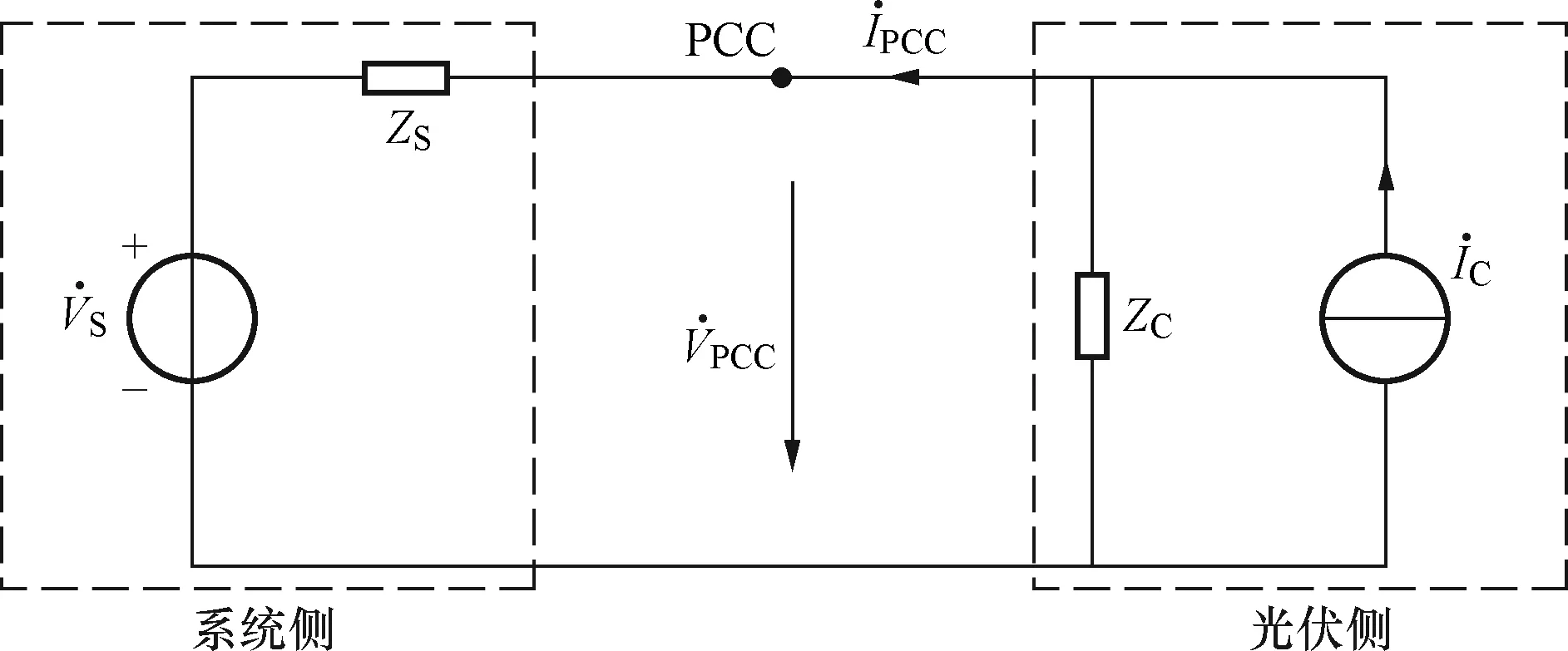
为系统侧谐波电压源；为光伏侧谐波电流源；ZS为系统谐波阻抗；ZC为光伏侧谐波阻抗；和分别为PCC处谐波电压和电流图2 系统和光伏侧等值电路Fig.2 Equivalent of system and photovoltaic

由图2可以得出：

(1)

(2)

根据国际电工委员会标准《电磁兼容第3部分：限值第6分部分：中、高压电力系统中畸变负荷发射限值的评估》(IEC61000-3-6)对谐波发射水平的定义，列出光伏系统谐波发射水平为

(3)

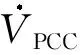
tn=y(xn)+εn

(4)

式(4)中：噪声εn～N(0,σ2),σ2为方差。

相关向量机回归函数表示为

(5)

式(5)中：K(x,xi)为核函数；ωi为权值系数；ω0为偏差。根据输出独立分布，训练样本集的似然函数为

(6)

式(6)中:t(xn)=(t1,t2,…,tN)T表示输出向量;Φ为维矩阵，Φ=[φ(x1),φ(x2),…,φ(xN)]T，φ(xn)=[1,K(xn,x1),…,K(xn,xN)]T。

为了避免过拟合现象，文献[18]通过贝叶斯定理获得了ω的先验分布:

(7)

式(7)中：αi(i=0，1，…，N)为超参数。

定义超参数αi和噪声方差σ2的超先验分布为Gamma分布，利用贝叶斯定理得到未知参数的后验分布：

(8)

权重向量ω的后验分布为

(9)

式(9)中后验分布的方差Σ和均值μ分别为

Σ=(σ-2ΦTΦ+A)-1

(10)

μ=σ-2ΣΦTt

(11)

A=diag(α1,α2,…αN)

(12)

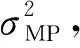
(13)

(14)

在迭代过程中绝大多数超参数都趋近于无穷大，对应的权重参数趋近于0，计算中核函数矩阵的很多项不考虑，使得矩阵稀疏化。若给一个新的输入x*，回归预测的方差和期望分别为

(15)

y*=μTφ(x*)

(16)

式中：y*为输入x*对应的输出。

使用RVM方法计算系统谐波阻抗步骤如下。

(2)选择高斯核函数设置带宽。

(3)初始化超参数α和σ2方差，根据式(13)、式(14)迭代求出最优值。

(4)求出权重向量分布。

(5)输入新的谐波电压、电流数据组成向量，由RVM模型回归预测出系统谐波阻抗。

2 仿真分析

根据图2所示等效电路编程计算，根据式(1)、式(2)得到1 000组PCC处谐波电压、电流数据，每60组数据进行递推计算，验证本文方法的正确性，参数设置参考文献[15]，具体参数设置如下。

(2)系统侧谐波阻抗ZS为(0.5+j1)Ω，光伏侧谐波阻抗ZC为(4.5+j7.8)Ω，两侧谐波阻抗的实部和虚部均加上20%正弦半波变化。

采用4种方法(方法1为文献[12]二元回归法，方法2为文献[13]的协方差法，方法3为文献[15]的支持向量机法，方法4为本文方法)计算系统谐波阻抗幅值相对误差方均根值和光伏系统谐波发射水平95%概率值的相对误差，结果如表1、表2所示。

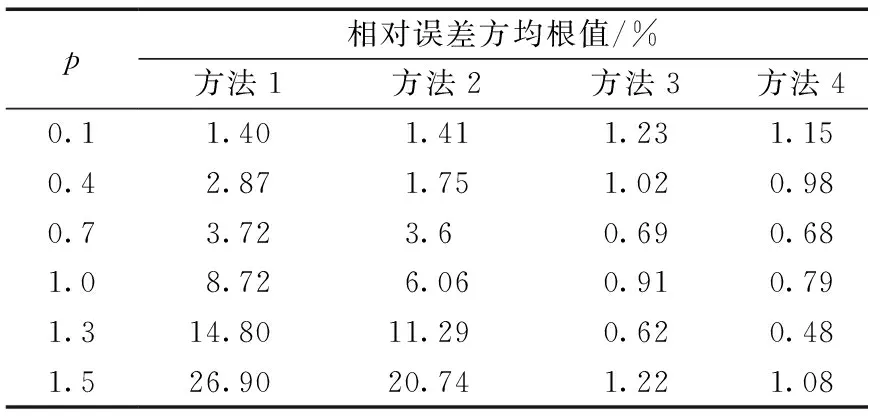
表1 |ZS|计算结果误差对比Table 1 Contrast of |ZS| calculation errors

表2 谐波发射水平误差对比Table 2 Contrast of harmonic emissions level errors

由表1、表2可知，随着p增大，即背景谐波增大，方法1(二元回归法)和方法2(协方差法)计算的系统谐波阻抗误差增大，谐波发射水平的误差也增大。方法1在背景谐波平稳时，计算精度较高，随着背景谐波波动增大，计算结果误差增大。方法2随着背景谐波增大，PCC处谐波电流与背景谐波的相关性增强，增加方法2计算的误差。方法3(支持向量机法)、方法4(本文方法)的计算结果均保持了较小的误差水平，其中方法4的误差更小，相关向量机回归相较于支持向量机回归，在计算精度上有所提高。

3 实测数据计算

实测数据来自于某光伏电站并网点110 kV母线，并网点处系统最小短路容量为2 800 MV·A，得出参考基波阻抗值为5.229 Ω。将某天12:30—14:30两个小时内采样数据，按每0.2 s进行傅里叶变换，得到的PCC处5次谐波电压和电流幅值波形，如图3所示。用仿真分析中的四种方法分别对5次谐波数据按每2 min(即600个数据点)进行分段递推计算，算出的系统谐波阻抗用图4表示。

图3 谐波电压电流波形Fig.3 Waveforms of the harmonic voltage and current

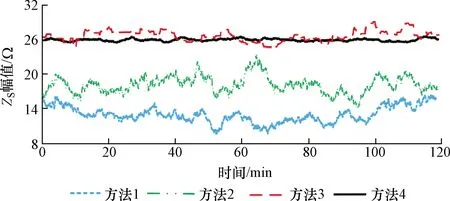
图4 系统5次谐波阻抗估计值Fig.4 Estimation of the 5th harmonic ZS

根据基波参考阻抗估算出系统5次谐波阻抗为26.145 Ω，如图4所示方法3和方法4计算的谐波阻抗幅值与该估算值相近，其中方法3利用支持向量机回归计算系统谐波阻抗，参数较多影响计算精度。光伏系统接入城市配电网，背景侧有大量的非线性负荷，背景谐波的不确定性较大。方法1在背景谐波稳定时有效，易受背景谐波波动影响。方法2 计算光伏并网点谐波阻抗时，背景谐波电压与PCC处谐波电流的相关性增强，导致计算结果误差增大。

采用4种方法估计的系统谐波阻抗，计算光伏系统谐波发射水平，结果如表3所示。

表3 光伏系统谐波发射水平95%概率值Table 3 95% probability values of the photovoltaic system harmonic emission levels

4 结论

利用相关向量机回归出系统谐波阻抗，进而求出谐波发射水平，通过仿真和实测数据计算可以看出，本文方法可以用于光伏并网点谐波发射水平的计算。利用相关向量机回归方法，避免了支持向量机回归参数多，影响计算精度的问题。

相关向量机核函数的选择主观性较强，使得构建的回归模型性能有限。下一步工作将研究如何组合多个核函数，提高模型性能。