基于小结构体的无线传感器网络部署算法

史佳琦，谭 励，唐小江，连晓峰，王浩宇

（北京工商大学计算机与信息工程学院，北京 100048）

（*通信作者电子邮箱tanli@th.btbu.edu.cn）

0 引言

覆盖优化是传感器网络研究中的一个重要的问题，是指将传感器放置在适当的位置，使得传感器覆盖的区域能够达到最大化，覆盖优化直接影响着传感器网络的性能。在未知的环境中部署大量的传感器节点可以提高传感器网络的可扩展性和可靠性［1］。对于覆盖问题现在已经有了很多的研究成果。Wang 等［2］提出了一种基于改进鲸鱼算法的无线传感器网络覆盖优化模型，实现了对感兴趣区域的全覆盖；Wang等［3］提出了一种基于粒子群优化的覆盖控制算法，先将传感器节点随机部署在目标区域并保持静止，然后，将传感器网络划分成若干个小传感器网络并计算出每个小传感器网络的覆盖率和能耗，最后根据每个划分出的网格的覆盖率和能耗对每个传感器节点的感应半径进行调整。樊富有等［4］利用量子遗传算法研究了复杂的监控环境下的无线视频传感网络的覆盖率问题，实验结果趋近于理想值；Habibi 等［5］使用基于梯度的非线性优化方法为每个传感器节点找到一个目标点，从而尽可能增加局部的覆盖率；何庆等［6］提出一种基于改进正弦余弦算法的节点部署优化方法，用较少的节点达到较高的覆盖率。以上方法主要对传感器节点的覆盖率进行了提升。

Lin 等［7］和Sung 等［8］研究了利用Voronoi 图的方法在二维空间内进行自主部署的算法。Fang等［9］提出了基于盲区质心的方案和基于干扰质心的方案，用来解决移动无线传感器网络中的覆盖问题，在基于盲区质心的方案中，每个传感器的Voronoi 盲区多边形首先是通过考虑相邻位置来确定的，然后将Voronoi 盲区多边形的质心作为各传感器的目标位置。在基于干扰质心的方案中，传感器首先在每一轮中根据基于中心的方案找到覆盖孔，然后在局部扰动和局部重构算子的作用下，移动到目标位置。Liao 等［10］对移动无线传感器中的连接问题进行了研究，证实传感器节点的移动性对连通性和覆盖率的影响。用Voronoi 划分的方法估计网络连接和目标覆盖所需要的传感器节点的最小移动量。Gao 等［11］详细讨论了可旋转摄像机传感器的全视野栅栏覆盖问题，介绍了一种新的加权图和两种集中式算法，该方法节省了传感器的节点个数同时也降低了时间复杂度。Li等［12］讨论了有向传感器和全向传感器的覆盖最大化移动传感器部署问题，得出同步旋转运动控制和分级旋转运动控制两种算法的最优性和复杂性结果。张军等［13］提出了一种新的混合无线传感器网络覆盖优化算法，对固定节点进行Voronoi 多边形划分；利用划分结果分析固定节点的覆盖盲区；利用基于反向学习策略的蜂群算法优化部署移动节点。林祝亮等［14］在网络覆盖率最优化的同时，有效减少网络迭代次数。在粒子进化的多粒子群算法的基础上提出了一种无线传感网络覆盖优化策略，通过多种群并行搜索，采取粒子进化理论使陷入局部最优的粒子迅速跳出，有效地避免了基本粒子群算法容易出现的“早熟”问题，提高了算法的稳定性。这些方法使用Voronoi 的方法在提高传感器节点覆盖率的同时考虑了算法的复杂度，但节点的迭代时间普遍较长，部署的复杂度也较高。

针对二维平面中的无线传感器网络节点的部署问题，本文在Voronoi 图算法的基础上提出了一种基于小结构体的无线传感器网络部署算法（Deployment Algorithm based on Basic Architecture，DABA），由于不同结构体之间存在孔洞问题，在覆盖率与Voronoi图算法覆盖率相近情况下，该算法能够提升部署效率，并且可以实现传感器节点部署过程中的避障。

1 基于小结构体的部署算法

1.1 小结构体描述

在传感器网络的部署中一般要求被部署的节点数量有一定的规模，使节点最终能够进行密集的覆盖，以此来避免在部署区域中出现覆盖漏洞。

由于二维部署区域较为广泛，而且单个传感器节点的能力有限，要使传感器节点能够覆盖到整个部署区域要求的节点数量很大，这会增加部署算法的复杂程度以及节点所需的迭代时间。为了解决这个问题，提出了“小结构体”的概念。小结构体是在应对复杂监测任务的时候，由若干个传感器节点组成，具备典型特征的最小结构单元。小结构体在部署过程中被当作一个整体进行部署，小结构体的内部结构不进行改变，整个无线传感器网络由若干个小结构体组成，共同完成复杂的监测任务。小结构体没有一个固定的结构，需要根据无线传感器网络的应用环境以及监测目标的特征和监测任务的复杂程度等各个方面进行综合考虑，设计适用于不同环境、不同监测任务的小结构体。

小结构体定义 采用六边形作为小结构体的基本结构。小结构体由7 个传感器节点组成，每个节点放置的位置分别对应六边形的6 个定点以及六边形的中心点。选择一个节点作为中心节点，通过中心节点来确定其余6 个成员节点的具体位置，如图1 所示。在本文中选取S1为中心节点，小结构体的边长。图2为基于六边形的小结构体的仿真。

图1 基于六边形的小结构体Fig.1 A basic architecture based on hexagon

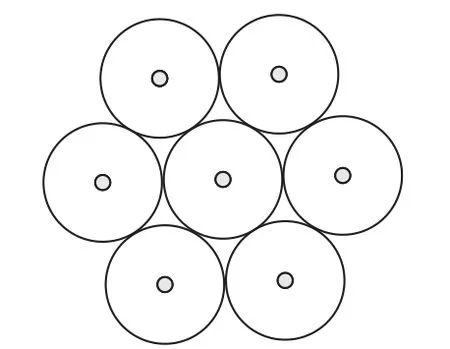
图2 基于六边形的小结构体仿真Fig.2 Simulation of basic architecture based on hexagon

设节点S1的坐标为(xS1，yS1)，则小结构体的中心P点的坐标计算公式如式（1）所示：

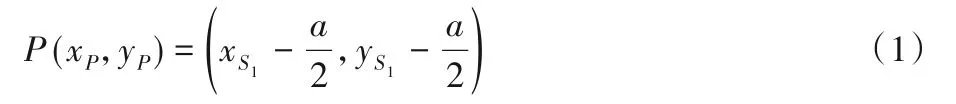
由P点坐标可以得到小结构体的中心坐标与小结构体其他成员节点坐标的映射关系，如式（2）所示：

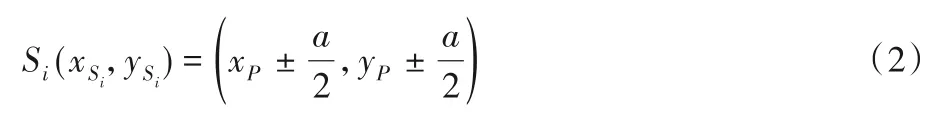
其中i的取值范围为｛1，2，3，4，5，6，7｝。

假设当前节点的坐标为Ci(xCi，yCi)，该节点的邻居节点集合的定义如式（3）所示：

其中：D(i，j)为节点Ci与节点Cj之间的欧氏距离；Dth为临界距离，决定两个传感器节点是否互为邻居节点。D(i，j)的计算公式如式（4）所示：

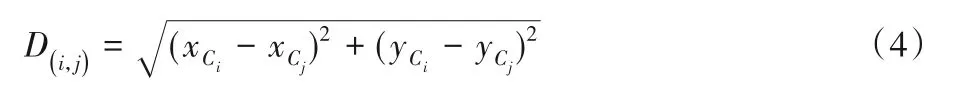
具体构建方法步骤如下：

1）对所有的传感器节点构建一个新的集合，用来存放节点。

2）标记每一个节点的状态，如果状态值为True则代表该节点没有与其他节点组成小结构体；如果状态值为False则代表该节点已经与其他节点构成小结构体。

3）遍历所有节点，判断当前节点的状态信息，如果当前节点的状态值为True，则转到步骤4）；如果当前节点的状态值为False，则转到步骤8）。

4）遍历当前节点的所有邻居节点的集合，统计邻居节点集合中状态值为True 的节点的个数，如果状态值为True 的邻居节点的个数小于7，转到步骤7）；如果状态值为True的邻居节点的个数大于等于7，转到步骤5）。

5）当前的节点与邻居节点集合中的前7个状态值为True的邻居节点构成小结构体，指定当前的节点为中心节点，构建基于六边形的小结构体，然后转到步骤7）。

6）将所有已经参与构建小结构体的节点的状态值修改为False。

7）如果已经遍历完所有的节点，则转到步骤8）；否则，遍历下一个节点，转到步骤3）。

8）结束退出。

1.2 DABA

本文提出的DABA 根据小结构体中心位置以及小结构体的半径构建二维Voronoi 图，计算每个小结构体所对应的Voronoi 区域的中心位置，使小结构体的中心位置移动到对应的Voronoi区域的中心，然后通过小结构体的中心与其他成员节点之间的映射关系，计算每个成员节点的位置，多次迭代完成部署。

具体的部署算法如算法1所示。

算法1 DABA。

输入：节点的个数N、节点的感知半径r、互为邻居节点的临界距离Dth以及区域的边界B；

输出：节点最终位置C'。

文献［12］提到的二维Voronoi 图构造的时间复杂度为O(nlogn)，本算法的时间复杂度为O(mn2logn)，n为节点的个数，m为迭代的次数。

1.3 避障设计

针对在实际部署中可能会出现障碍的情况，算法设置障碍点，作为实际部署环境中可能会出现的不能进行部署障碍点的模拟。障碍点是在构建完小结构体之后添加的一个点，这个点和其他节点不同，它在整个部署过程中是不动的且不能与其他节点组成小结构体，同时其他节点在部署过程中要避开这个点。障碍点可以看作一个特殊的单独节点。

2 仿真与结果分析

2.1 仿真实验

本文实验采用Python2.7 作为仿真环境，CPU 型号为Inter Core i7 6700T，监测区域大小设置为200 m ×200 m 的二维平面，初始时，所有节点随机部署在整个二维监测区域内，障碍点通过固定坐标的方式添加到二维平面中，节点的感知半径为5 m，障碍点的半径为15 m，节点个数为602。仿真实验中涉及到的相关参数如表1中所示。

表1 实验参数Tab.1 Experimental parameters

本实验选取四组不同Dth值进行仿真，Dth的值分别为10、15、20和1 000四个取值，分别用两倍的感知半径、三倍的感知半径、四倍的感知半径和全区域内所有节点互为邻居节点这五种情况。通过构建小结构体，采用二维Voronoi图的方法在二维平面的目标监测区域内完成部署算法以及小结构体绕开障碍点的情况的仿真。未与其他节点组成小结构体的单个节点，视为一种特殊的小结构体，单个节点与其他小结构体同等级别参与部署算法。图3 为Dth=10时节点的部署情况以及躲避障碍点的情况。

图3 Dth=10的部署情况Fig.3 Deployment situation with Dth=10

2.2 结果分析

本文主要通过以下3 个指标对所提出算法的性能进行评估：

覆盖率 判断传感器网络性能十分重要的一个指标，反映了传感器网络对于所需监测区域中监测对象的全面监测能力：

部署时间 指的是在整个部署的过程中，使节点尽可能多地覆盖区域，也就是当覆盖率达到一个相对稳定状态时所需要的时间，由于涉及的两种算法都需要先构造Voronoi区域且所需时间差别不大，部署时间从节点开始移动时，即节点开始迭代时算起：

移动距离 指的是在整个部署的过程中，节点在部署时间内进行移动的距离，即节点从初始的地点到最终部署情况的地点所移动的距离：

其中：xfinal、xinitial为节点最终横坐标、节点初始横坐标；yfinal、yinitial为节点最终纵坐标、节点初始纵坐标。

从图3 的最终部署情况看出基于小结构体的部署算法能够较好地对二维平面进行覆盖，Dth=10 的情况下部署效果最佳，这说明DABA 能够较好地对需要部署的二维平面进行部署，但要依据部署情况选择互为邻居节点的临界值以便能够达到更好的部署效果。躲避障碍的情况中互为邻居节点的临界值为两倍半径，即Dth=10 的情况下小结构体躲避障碍点的效果最佳，节点可以全部躲避开障碍点后进行部署。

图4 为Dth=15、Dth=20 以及Dth=1 000 的情况下节点的最终部署情况以及躲避障碍点的情况。

图4 最终部署及躲避障碍点的情况Fig.4 Final deployment and obstacle avoidance situation

在互为邻居节点的临界值分别为Dth=15、Dth=20 和Dth=1 000 的三种情况下都存在有节点不能完全避开障碍点的情况，并且从对比图中可以看出，在基于小结构体的二维部署情况下，参与部署的节点的个数越多，节点躲避障碍点的效果越好。

下面将从覆盖率、部署时间以及移动距离这三个指标分别将基于小结构体的二维部署算法与Voronoi 图方法进行对比，验证本文中所提出算法的有效性。

在图5中，将二维Voronoi 图方法和本文提出的基于小结构体方法的四种情况进行了对比。其中：3dDABA-A表示Dth=10，3dDABA-B 表示Dth=15，3dDABA-C 表示Dth=20，3dDABA-D表示Dth=1 000。从图5 可以看出，当迭代次数不断增多的时候，基于小结构体算法中的四种情况的覆盖率都逐渐增大，最终区域平衡。虽然覆盖率低于Voronoi 图方法但差距不大。当Dth=10时的覆盖率最大，能够达到92%左右。

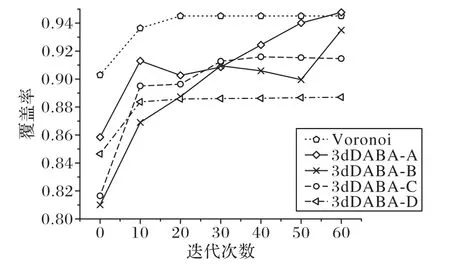
图5 覆盖率变化图Fig.5 Coverage rate change diagram

图6中将二维Voronoi 图方法和文中提出的基于小结构体方法的四种情况下算法再部署过程中每个节点每次迭代的平均移动距离进行了对比。从图6中可以看出，随着迭代次数的不断增加，四种情况下每个节点的平均移动距离都在不断减小，最终趋近于0，算法最终收敛。每个节点在部署过程中都不断趋于静止，表明网络在逐渐达到一个稳定的状态。从结果中看虽然本文提出的算法中节点的平均移动距离高于二维Voronoi图方法的移动距离，但是差距并不是很明显。

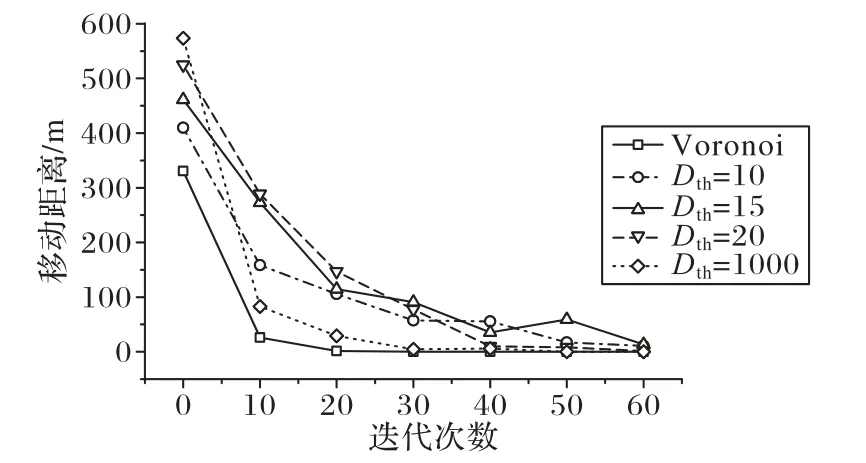
图6 每个节点每次迭代平均移动距离Fig.6 Average travel distance of different nodes in each iteration

图7 将二维Voronoi 图方法和文中提出的基于小结构体方法的四种情况下的节点迭代的部署时间进行了对比。从图7中可以看出，基于小结构体的部署算法在节点迭代的部署时间方面的优势较为突出。与二维Voronoi图方法相比较：互为邻居节点的临界值为两倍半径，即Dth=10 情况下算法节点迭代的部署时间是它的1/3；互为邻居节点的临界值为三倍半径，即Dth=15 情况下的算法节点迭代的部署时间是它的1/9；互为邻居节点的临界值为四倍半径（Dth=20）和互为邻居节点的临界值不限（Dth=1 000）的算法节点迭代的部署时间更是远远小于Voronoi图方法的部署时间。

图7 部署时间随迭代次数变化Fig.7 Deployment time varying with number of iterations

在图8中，通过将二维Voronoi 图方法中节点个数与文中提出的基于小结构体的方法的四种情况中小结构体的个数进行了对比。从图8中可以看出，构造小结构体之后，参与构造Voronoi 图的节点数量有了很大幅度的下降，因此这能够有效地降低构造Voronoi 图的复杂度，从而降低整个算法的复杂度。在仿真实验中：在互为邻居节点的临界值为四倍半径，即Dth=20 情况下参与构造Voronoi 图节点的数量约为二维Voronoi 图方法中参与构造Voronoi 图节点数量的1/3；互为邻居节点的临界值不限，即Dth=1 000情况下参与构造Voronoi图节点的数量约为Voronoi 图方法中参与构造Voronoi 图节点数量的1/6。

通过仿真结果的比较，可以发现文中所提出的算法在部署时间这一方面有着非常明显的优势，覆盖率在某些情况下可以超过Voronoi 图方法，虽然覆盖率不及Voronoi 图方法但差距并不明显。节点每次迭代的平均移动距离方面高于二维Voronoi 图方法的移动距离，但是差距并不是很明显。通过综合部署时间、覆盖率以及平均移动距离这三个衡量指标，可以发现，当互为邻居节点的临界值为两倍半径，即Dth=10情况和互为邻居节点的临界值为三倍半径，即Dth=15 情况时的这两个方案效果是最好的。在实际部署情况中可根据部署节点数量以及需要覆盖情况和要求完成时间选择Dth值，尽可能减小临界值，使覆盖率更高。

图8 不同条件下小结构体个数Fig.8 The number of basic architectures under different conditions

3 结语

针对二维平面中的无线传感器网络节点的部署问题，本文提出了基于小结构体的无线传感器网络部署算法（DABA），提出了小结构体的概念，通过仿真实验分析了算法的覆盖率、部署时间以及移动距离，并与二维Voronoi 图方法进行比较。实验结果表明本文算法在部署时间上有明显的优势，同时可以减少参与构造Voronoi 图的节点数量，有效地降低构造Voronoi图的复杂度，从而降低整个算法的复杂度。下一步将研究三维或其他复杂的环境中节点的部署方法。