5G低密度奇偶校验码的低复杂度偏移最小和算法
陈发堂,张友寿,杜 铮
(重庆邮电大学通信与信息工程学院,重庆 400065)
(*通信作者电子邮箱1375743499@qq.com)
0 引言
低密度奇偶校验(Low Density Parity Check,LDPC)码作为一种最佳纠错码之一,具有显著的编码性能和效率,近年来受到了广泛的研究关注[1]。在许多情况下,它展现出比Turbo码更好的译码性能[2-3],因此LDPC 码被多种通信标准采用[4]。此外,已经确认在增强移动宽带(enhanced Mobile BroadBand,eMBB)场景的5G系统中采用LDPC码,满足5G新无线(New Radio,NR)的高吞吐量需求。
LDPC码是具有稀疏奇偶校验矩阵的线性分组码,其校验矩阵可以用Tanner图描述[5],图中包含变量节点和校验节点,变量节点和校验节点之间的连接用边表示。置信传播(Belief Propagation,BP)算法,也称为和积(Sum-Product,SP)算法[6]通过迭代使LDPC 码的译码性能接近香农极限。信息在变量节点和校验节点之间反复传递。SP 算法虽然性能好,但是需要对数等复杂运算,给硬件实现带来了困难。为了降低复杂度,提出了最小和(Min-Sum,MS)算法,将校验节点中的对数转换为比较和求和来简化复杂的计算[7]。与SP算法相比,MS算法存在扩大校验节点消息幅度值的错误,导致性能出现损失。为了减少错误,提高性能,提出了两种改进算法,分别称为归一化最小和(Normalized-MS,NMS)算法和偏移最小和(Offset-MS,OMS)算法[8]。OMS算法使用求和系数改进MS中校验节点的结果;NMS算法中使用乘法系数,虽然提高了译码性能,但是引入的修正系数与实际期望因子值的差异使得译码性能不如BP算法。而且MS和两种改进算法要求在矩阵的每一行中计算第一和第二最小值,增加了复杂度。为进一步降低复杂性:单最小值最小和(single-minimum MS,smMS)算法仅使用一个常量纠正系数简化了第二最小值计算,却损失了部分性能[9];在此基础上提出的简化可变权最小和(simplified variable weight MS,svwMS)算法[10-11],引入随迭代次数变化的加权因子维持第一和第二最小值的比例,性能得到了提升,却增加了复杂度。
另一方面,近年来人们对LLR-BP译码算法的错误类型进行了研究[12],其中一种就是变量节点的振荡性。这种振荡性被视为变量节点更新前后LLR 消息值符号发生了变化,最终导致译码器无法收敛[13-14]。变量节点的振荡现象与检验矩阵的结构相关而与译码算法无关,出现在几乎所有的BP算法中而且并没有得到足够的重视。
为了解决以上问题,一种新的改进偏移最小和的算法被提出。密度进化理论(Density Evolution,DE)是分析LDPC 码译码算法性能,确定关键参数最佳值,并评估有限量化效果的一种重要方法。本文使用密度进化理论计算最佳的偏移因子值,克服了传统OMS 算法的不足,提高了译码性能,并使用线性近似方法对获取的最佳偏移因子进行近似处理,降低算法的实现复杂度。现有BP 算法中变量节点振荡性问题也被讨论,并提出了一种处理振荡性的方法,将节点更新前后的LLR消息值加权处理。仿真结果说明与其他改进MS算法相比,所提算法不仅提高了译码器收敛速度,而且改进了在中高信噪比下的纠错性能,且具有复杂度较低的优势。
1 LDPC码及其译码算法
1.1 LDPC码的表示方法
5G NR 标准LDPC 码的校验矩阵H包括N列和M行,其中M=N-K,N代表变量节点数,M代表校验节点数,可由基矩阵HBG定义。HBG包含Mb行和Nb列,基矩阵每个元素都映射到H中的一个维度为ZC×ZC子块矩阵。用全0 矩阵去替换HBG中的-1 值,用循环置换矩阵I(pi,j)替换HBG中的1 值,其中I(pi,j)是维数为ZC×ZC的单位矩阵右循环pi,j次获得,ZC是矩阵的扩展因子。LDPC 码的校验矩阵也可用Tanner 图表示,如果H(i,j)=1,表示在Tanner 图中第i校验节点与第j变量节点之间相连。假设校验矩阵如下:

对应的Tanner图如图1,其中ci和vi分别表示校验节点和变量节点。令N(m)={n:H(m,n)=1}表示与校验节点m相连的变量节点集合,M(n)={m:H(m,n)=1}表示与变量节点n相连的校验节点集合,同时让N(m) 表示排除变量节点n的变量节点集合,M(n)m表示排除检验节点m的变量节点集合。把校验节点m传递给变量节点n的消息称为C2V(Check-to-Variable)消息,用Lm→n表示;同理把变量节点n传递给校验节点m的消息称为V2C(Variable-to-Check)消息,用Zn→m表示。
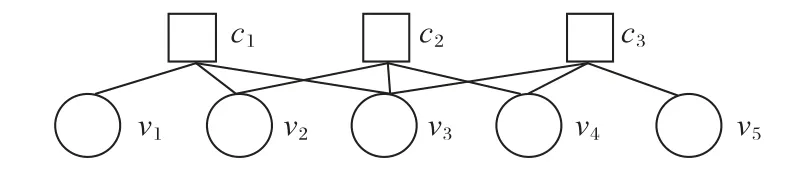
图1 LDPC码的Tanner图表示Fig.1 Tanner graph representation of LDPC codes
1.2 LLR-BP算法
LLR-BP 算法的核心是对校验节点和变量节点之间传递的外部消息进行迭代处理,并利用校验方程的约束提高译码的可靠度。译码步骤[15]如下。
1)初始化:计算变量节点vn接收到的信道消息值ln=。
2)迭代过程如下:
校验节点更新(C2V):
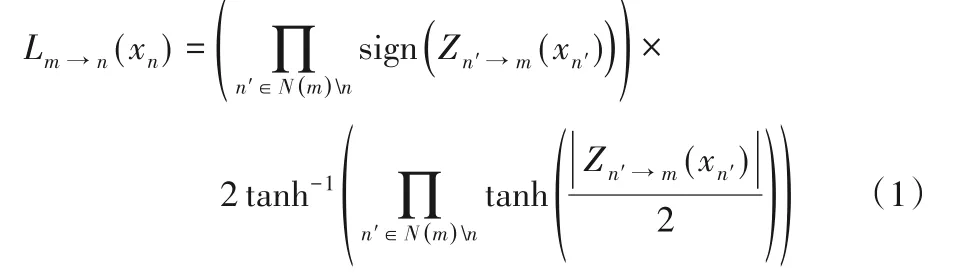
变量节点更新(V2C):

3)硬判决:
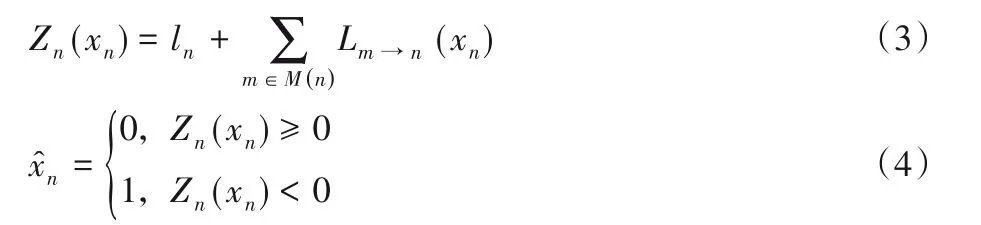
4)终止条件:如果满足X⋅HT=0 或者达到最大迭代次数时译码终止并返回译码结果;否则重复第2)步。
1.3 MS和OMS算法
MS 算法是对BP 算法迭代过程中的C2V 消息进行简化,其余处理不变[16],如式(5)所示。显然MS算法计算比较简单,但降低了译码性能。OMS 算法对MS 算法进行了改进如式(6)[17],使得该算法的译码性能接近BP算法。
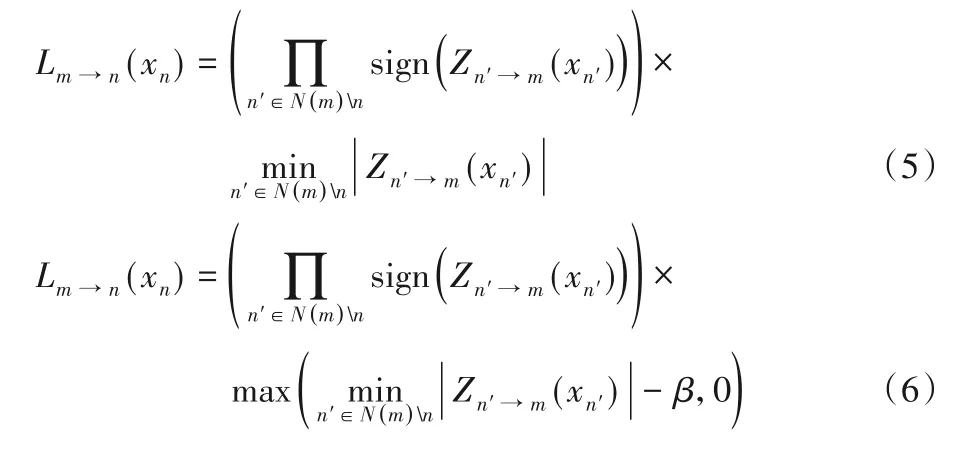
2 改进的OMS算法
2.1 基本知识
当把C2V 消息表示为符号和幅值时,从译码准则可以看出,符号用来译码,幅值表示消息的可靠性。与LLR-BP 算法相比,MS 算法高估了C2V 消息的幅值,所以译码性能下降。通过引入一个常数β来改善MS 算法中的校验节点幅值过大的错误,被称为OMS 算法。让L1和L2分别代表LLR-BP 算法和MS算法的C2V消息如式(7)和(8):
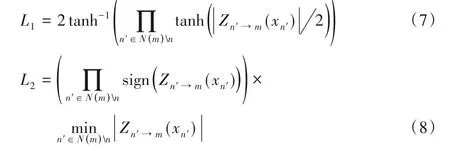
第一次迭代时的β可以通过式(9)计算得到,其中通过式(10)和式(11)[18]计算:
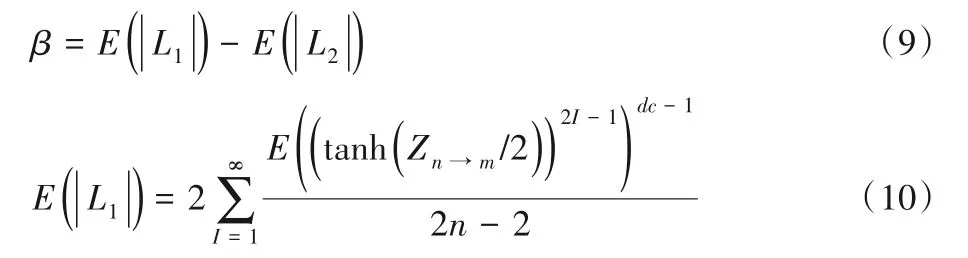
其中:dc代表检验节点的度,由无穷项的和组成,但通常取前几次之和用作近似[18]。
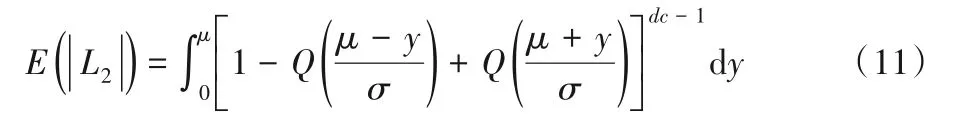
Q(⋅) 代 表V2C 消息的概率密度函数(Probability Distribution Function,PDF),由信道消息初始化:Q(x)=,μ=4/N0,σ2=8/N0。
一般做法,会在所有的迭代中使用相同的β值以达到简化译码处理的效果。然而,真实的β值与迭代次数有关。如果β的值随着迭代次数变化而变化并用于迭代译码,这样才能彻底改进译码性能,因此提出一种基于密度进化(Density Evolution,DE)计算每次迭代β值的方法。
在引进密度进化(DE)理论之前,说明两点:1)在使用DE理论进行求值时,有必要对消息进行量化。需要的是V2C 消息的概率质量函数(Probability Mass Function,PMF)而不是概率密度函数[19]。2)使用Matlab工具可以获取每次迭代中V2C消息的PMF。
2.2 基于DE的最优β值计算
首先,用L3表示OMS 算法中C2V 消息,如式(12),其中k代表迭代次数:
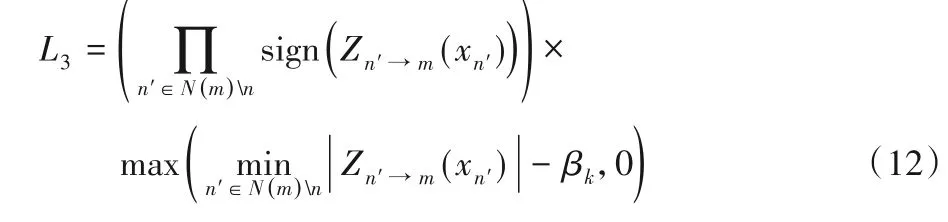
均值E(|L3|)由式(13)计算得到:
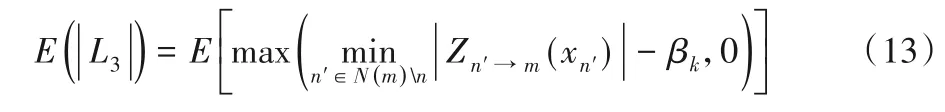
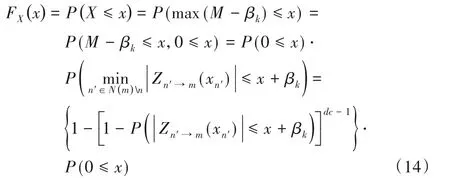
每个量化点的PMF由式(15)计算,其中s代表量化步长:
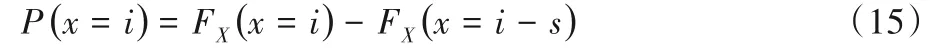
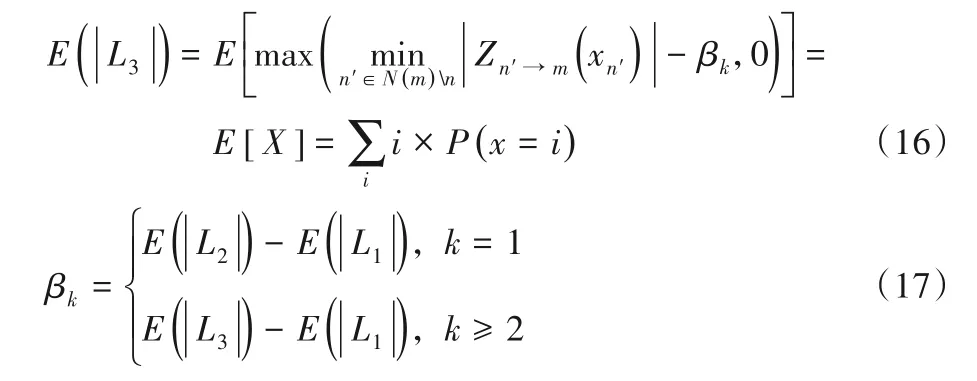
2.3 迭代次数与不同的译码算法
基于DE 理论计算得到的偏移因子βk与迭代次数的关系如图2 所示。在相同的信噪比下经过几次迭代过后,βk的值越来越小并收敛于0。这说明L3的概率密度函数非常接近L1的概率密度函数,而且偏移因子的值对译码的影响越来越小。说明本文所提译码算法是正确的。
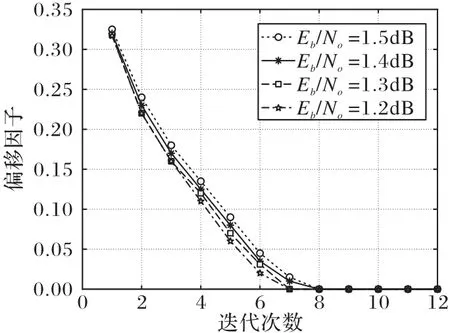
图2 偏移因子与迭代次数的关系Fig.2 Relationship between offset factor and number of iterations
理论上,在不同的信噪比下每次迭代使用不同的βk,则译码性能能够得到提升。然而这会增加硬件复杂度。为了降低复杂度,对前5 次迭代的βk值采用加权平均处理[20]。改进的偏移因子的值如式(18),其中λk是加权平均系数,对应分别设置为λ1=0.25,λ2=0.25,λ3=0.2,λ4=0.2,λ5=0.1。使用该方法改进的β被称为DEOMS-1算法。

另外从图2 可以看出,在每个信噪比下偏移因子与迭代次数的曲线斜率近似于常量,并且易于计算。于是提出一种线性近似方法,这种关系可写为:

于是式(18)可以近似等价于式(20):

由于LDPC 码的校验矩阵中变量节点存在两个及以上的环,同时节点正确和错误的LLR 消息在这些环中循环传递并在不同时刻到达该变量节点,造成变量节点振荡现象,导致译码器无法收敛。该现象与校验矩阵的结构有关,出现在几乎所有的BP 译码算法中。然而最近所提出的译码算法并未采用特定方法消除变量节点的振荡性。当变量节点发生振荡,很难区分更新前后的LLR 消息哪个是正确的,或者达到稳定状态。为了减弱其对迭代译码的影响,本文对变量节点更新前后的LLR 消息进行加权处理,减弱变量节点LLR 消息的振荡,提高译码的收敛性。具体处理规则如下:
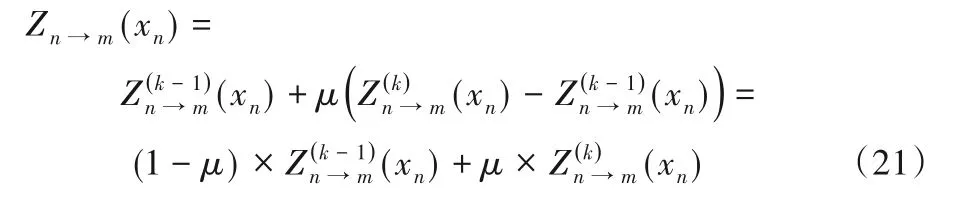
用式(21)计算得到的Zn→m(xn)值替换式(2),其中k为迭代次数,μ是加权系数,经实验本文最终选取μ等于0.5,则式(21)可以简化为:
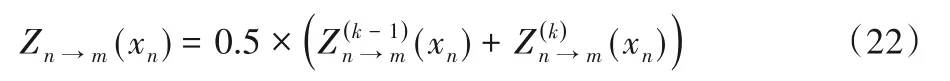
该方法稍微增加了复杂度,但可以很好地降低振荡影响,加快收敛。基于以上方法提出vwDEOMS-3算法。
3 仿真结果分析
本文使用5G NR 标准构造的准循环LDPC(Quasi Cyclic Low Density Parity Check,QC-LDPC)码对不同译码算法LLRBP、MS、NMS、OMS的译码性能进行仿真并与本文所提出的低复杂度偏移最小和算法的译码性能进行比较。选择5G NR LDPC 码的基矩阵HBG2,采用信息长度K=1 000,码字长度N为2 500,码率R为0.4,评估了不同信噪比下各译码算法的误码率性能。在码率为0.4时NMS 算法的归一化因子取值0.65。所有的仿真都在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道模型下,经过BPSK(Binary Phase Shift Keying)调制,最大迭代次数设置为30,每个信噪比下设置帧数为2 000。
图3 展示了不同译码算法的误比特率(Bit-Error Rate,BER)性能比较,显然LLR-BP 译码算法拥有最佳的性能。在BER 为10-5时,相对于LLR-BP 算法,MS 算法性能损失接近1.2 dB,这是校验节点的幅值过大造成的。与MS 算法相比,OMS 算法与NMS 算法的译码性能可以获得0.6~0.8 dB 的增益,但是还与LLR-BP 算法的译码性能相差0.4~0.6 dB,说明虽然引入了校正因子对MS算法进行改进,但是该校正因子并不是最佳的值。DEOMS-1 算法使用更准确的偏移因子,在BER 为10-5时,相比MS 算法可以获得大约1 dB 的增益。在BER 为10-5时,DEOMS-2算法与DEOMS-1算法误码性能非常接近,大约只有0.01 dB 的差距,说明线性近似处理是合理有效的;而vwDEOMS-3 算法比OMS 算法的性能提高约0.5 dB,比NMS 算法提高约0.3 dB,与LLR-BP 算法相比性能上也只相差近0.1 dB。通过使用更接近真实的偏移因子和削弱变量节点的振荡性,所提算法可以实现较好的译码性能和迭代性能。
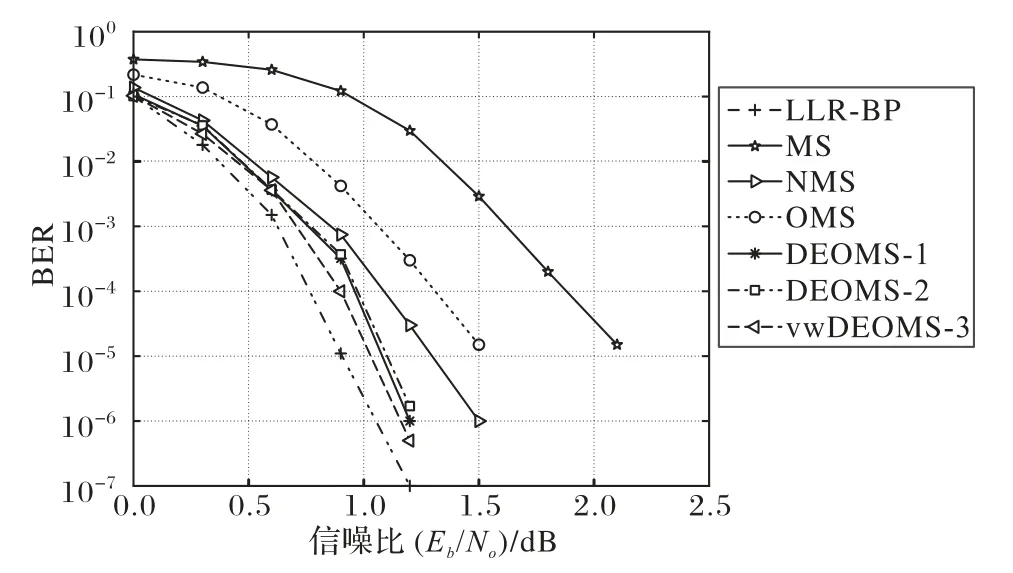
图3 不同算法的误比特率性能对比Fig.3 BER performance comparison of different algorithms
4 复杂度分析
结合上面的分析,表1 给出了不同译码算法的校验节点更新操作中的计算复杂度。可以看出LLR-BP 算法需要更多的乘法操作,复杂度最高,其次是MS 算法、NMS 算法、OMS 算法。DEOMS-1 算法中的偏移因子是基于密度进化计算的,增加了些许复杂度,但极大提高了译码性能,考虑到这一点,DEOMS-2 算法采用线性近似方法,进一步降低计算的复杂度。vwDEOMS-3 算法对变量节点的加权操作在硬件资源上并不需要多余的乘法器,只是信息位的右移。本文使用Matlab 计算最优的偏移因子值并保存在硬件中,而不会消耗多余的硬件资源。经典的OMS 算法通过蒙特卡洛方法获取偏移因子或者仅仅基于DE 计算第一次迭代时得到的偏移因子的值,需要大量的加法和比较操作,计算复杂度总体来说较高。总的来说,DEOMS 算法拥有较低的计算复杂度和较少的译码延迟,译码性能也有0.3~0.5 dB的提升。

表1 不同算法校验节点消息计算复杂度Tab.1 Check node message computational complexities of different algorithms
收敛速度是衡量LDPC 算法复杂度和译码性能的另一个关键指标,图4 使用平均迭代次数来评估各种算法的收敛速度。显然,相比其他算法,MS 算法和OMS 算法需要更多的迭代次数。可以观察到,与MS算法相比,所提出的DEOMS算法的平均迭代次数得到显著降低。尽管LLR-BP 算法的迭代次数略低于所提的DEOMS算法,但由于其检验节点操作的复杂度较高,每次迭代都可能花费大量的计算时间,而DEOMS 算法拥有较小的译码延迟。从图中可得到的另一个重要结论是DEOMS-2算法的平均迭代次数非常接近DEOMS-1算法,这证明DEOMS-2算法对迭代次数的影响非常轻微。而vwDEOMS-3 算法的平均迭代次数比DEOMS-1/2 算法有所改进,说明该算法是合理有效的。
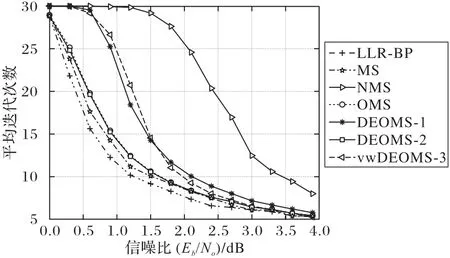
图4 不同算法的平均迭代次数Fig.4 Average numbers of iterations of different algorithms
5 结语
本文提出了一种5G LDPC 码的低复杂度偏移最小和算法,所提算法的优点是使用密度进化理论获得了最佳的偏移因子,并对其使用线性近似方法进行处理,降低了计算复杂度;提出了一种处理变量节点振荡性的方法,对变量节点LLR消息加权处理,加快了译码器的收敛。仿真结果表明,对于5G NR 标准的QC-LDPC 码,所提算法与MS 及其改进算法相比存在误码性能和迭代次数优势。

